竖向循环荷载下钙质砂单桩沉降特性模型试验研究

王 帅，雷学文，孟庆山，许洁丽，王明昭，郭 威

(1.武汉科技大学 城市建设学院，武汉 430065； 2.武汉建工集团股份有限公司 企业技术中心,武汉 430056； 3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071； 4.武汉科技大学 汽车与交通工程学院, 武汉 430065)

1 研究背景

钙质砂广泛分布于地球南北纬30°之间，它在中国南海诸岛、红海、阿拉伯湾南部、印度西部海域、巴斯海峡等海域均有分布。过去几十年里，在钙质砂地层上建造的建筑物越来越多[1]，钙质砂主要成分为CaCO3，含量在50%以上，具有疏松多孔的结构，在常应力水平作用下，即会发生颗粒破碎[2-3]。桩基通常被用于承担构筑物荷载，有别于陆地，岛礁工程的桩基除承受建筑自重的恒载外，还经常承受不同幅值大小的动力荷载，例如往复交通荷载、吊车往复荷载、风浪等循环荷载[1]。

诸多现场试验表明，现有桩基设计经验在钙质砂地层中并不完全适用，一系列工程事故[4-6]使人们认识到钙质砂桩基不同于普通陆源砂土中的承载特性[7-9]，具有较低的侧摩阻力和桩端阻力，沉降规律和形式也有其自身特点。Poulos[10]在砂土中进行了循环加载桩基模型试验，与静载相比，循环荷载下桩基主要有3个方面的问题值得关注：①桩土界面强度或刚度的降低；②发生破坏的临界循环次数；③桩顶的累计变形规律。这些也是工程中普遍关心的问题。与此同时，Poulos等[11]研究认为在高循环应力水平下，循环荷载导致的土体变形会使钙质砂中桩端承载力降低。Chan等[12]在砂土中开展循环桩基试验，研究桩顶累计沉降、沉降速率与循环加载次数的关系，认为循环荷载影响桩顶沉降速率变化，桩的行为可根据沉降速率稳定与否进行划分，桩基的沉降稳定与否与循环荷载相关，并且关系到工程构筑物的安全性和稳定性，循环荷载对钙质砂中桩基沉降影响更加复杂，其机理值得深入研究。

钙质砂桩基试验主要采用室内模型试验与现场桩基测试手段。Yong[13]用铝合金和混凝土制成两种模型桩，通过模型试验手段，研究钙质砂和石英砂中桩侧摩阻力特性。江浩等[14]、秦月等[15]、杨超等[16]也开展了钙质砂桩基承载特性模型试验，研究了静荷载下钙质砂单桩沉降规律和承载特性，但未对循环荷载下钙质砂单桩沉降规律及其机理开展研究。而循环荷载下桩基的现场测试多为工程类试桩，受限制于现场条件，其循环加载次数一般较小(多为 6～200 次)。Al-douri等[17]进行了循环荷载下钙质砂桩基室内模型试验，其循环次数最大为250次。对于承受长期循环荷载的钙质砂桩基而言，该循环次数水平有一定局限性。在陆源不易破碎土体中开展的循环荷载下桩基模型试验[18-19]，未涉及土体颗粒破碎的问题，循环荷载幅值水平较为单一。

钙质砂中桩基础服役环境通常伴随循环荷载，例如岛礁施工吊车的往复荷载、道路碾压的交通荷载、高承台桩基承受上部桥梁和列车移动荷载[19]，这些荷载多数是恒载和动载同时作用的循环荷载[19]。循环荷载下桩基的沉降规律和机理是桩基工程的重要研究内容。本文在自行研制的试验装置上开展了钙质砂单桩竖向循环荷载室内模型试验，与前人相比，该装置在功能上更为精确，通过液压加载系统可循环加载2 000次。利用传感器进行实时数据采集,分析了动荷载比对钙质砂中模型桩累积沉降规律的影响，探究其机理。试验结果对珊瑚礁桩基础的设计具有重要的参考价值。

2 试验概况

2.1 试验材料

试验所用钙质砂取自中国南海某岛礁，是一种未胶结松散碎屑物，试验前去除杂质，采用振动筛分法测定其颗粒级配，得到试验颗分曲线如图1所示。其不均匀系数Cu=3.66，曲率系数Cc=1.06，为级配不良砂，含水量ω=5.5%，测得试样的基本物理性质如表1所示。

图1 颗粒筛分曲线Fig.1 Particle distribution curve

表1 试样基本物理性质Table 1 Basic physical properties of test samples

2.2 试验装置

试验在中国科学院武汉岩土力学研究所研制的钙质砂多功能桩基模型试验装置[20]上完成。该装置通过液压控制系统模拟实际的工况荷载，可施加具有恒载和不同大小动载的循环荷载，通过动静数据采集仪实时获取传感器(电位移计、土压力盒)数据，装置如图2。模型桩顶部高精度电位移计(精度0.001 mm，量程为50 mm)用于采集模型桩竖向位移。桩端安装土压力盒，测量桩端底部土压力值q。试验装置通过动态采集仪获取数据，可分析不同动荷载大小下钙质砂单桩沉降和承载规律。

图2 试验装置示意图Fig.2 Schematic diagram of test device

2.3 模型箱和模型桩

模型箱为边长800 mm、高1 000 mm、壁厚10 mm的钢性箱体。模型桩直径为50 mm、壁厚2 mm、长1 000 mm的闭口铝管桩，相似比为1∶20，模型箱边距离模型桩外壁距离(B)与模型桩直径(b)边界比B/b为16，远大于模型试验理论上要求的边界比2.82，能够有效消除边界效应[21]。模型桩底部安装微型土压力盒，桩外壁压花粗度处理，试验按照图2所示，在模型箱中安放模型桩，保持桩身垂直，桩身埋入深度800 mm，上部露出200 mm。采用分层填筑法，相对密实度为Dr=0.55，按公式Dr=[ρdmax(ρd-ρdmin)]/[ρd(ρdmax-ρdmin)],计算出控制密度ρd=1.47 g/cm3。进行模型地基填筑时，每隔10 cm装填同等质量的钙质砂，填筑时使用木板进行抹平，并采用木板静压法配合橡皮锤方法压实到指定高度[15]。

2.4 试验方案

2.4.1 桩基静荷加载试验

采用快速荷载维持法逐级加载，荷载增量ΔP=0.5 kN，每级荷载维持时间T=30 min。定义桩顶静载累计沉降量为SP，当SP超过1倍桩径(50 mm)时停止加载，开展平行试验3次，计算SP平均值，绘制P-SP曲线，并确定单桩极限承载力特征值Qc。

2.4.2 桩基循环加载试验

循环荷载包括恒载和荷动载两部分。定义恒载为Q1，定义动荷载为Q2。定义恒定荷载比λ=Q1/Qc，动荷载比M=Q2/Qc。桩基础在服役期内，其恒载大小相对稳定，动载往往在一定幅度内变化，参照文献[16]—文献[19]，设计单桩恒载Q1=0.2Qc，动荷载比M=0.15、0.25、0.35、0.45、0.55。加载方案如表2。周期T为4 s，波形如图3。试验荷载大小变化如式(1)所示。

图3 试验荷载波形Fig.3 Waveform of test load

表2 试验加载方案Table 2 Test loading schemes

P=Q1+Q2=0.2Qc+MQc|sin(ωt)|,

t>t1。

(1)

式中：t为时间；t1为首次循环荷载加载时间。

目前循环荷载单桩破坏值尚无统一标准，定义循环桩顶循环累计沉降为SN，定义桩顶循环累计沉降SN幅值为SNf，桩顶循环沉降破坏值为SNP。参考文献[22]取50%Qc值对应静载累计沉降SN为循环沉降破坏值SNP。考虑到试验装置实际性能，当循环次数N=2 000次时停止试验，开展平行试验3次，取计算平均值，绘制N-SN曲线。

3 试验结果

3.1 桩顶累计沉降

3.1.1 静荷加载桩顶沉降

图4为竖向荷载P与桩顶静载累计沉降SP关系曲线。由图4可见，SP随P的增大而逐渐增大，呈现出OA-AB-BC三段式发展。OA段，竖向荷载P较小，SP不明显，当P=2.5 kN时，SP仅为-1.8 mm。AB段，SP随P的增大而增大，呈现渐进式。到达B点时，当P=9.5 kN时，P-SP曲线出现位移拐点，SP出现陡降。而BC段，SP几乎呈直线型增长。按照《建筑桩基技术规范》(JGJ 94—2008)[23]中方法，确定单桩极限承载力特征值Qc=9 kN，循环荷载施加恒载Q1=0.2Qc=1.8 kN。桩顶循环沉降破坏值为静载P=4.5 kN时的累计沉降量3.2 mm,桩顶循环沉降破坏值SNP=-3.2 mm，在此基础上进行循环加载试验。

图4 P-SP曲线Fig.4 P-SP curve

3.1.2 循环加载桩顶沉降

图5为不同动荷载比M下桩顶循环累计沉降SN与循环次数N关系曲线。由图5可见，SN随N的增加而逐渐增大，在循环加载前期SN增长较明显，随后增长趋势弱化。动荷载比M对桩顶循环累计沉降量终值SNf影响显著。当循环次数相同时，动荷载比M越大，SNf越大。当M=0.15、0.25时，其SNf分别为1.988 mm和2.620 mm，变化量不明显。但当M=0.35时，在N=28次时，SN已达到SNP(3.2 mm)，M>0.35桩基循环沉降才发生破坏，表现出类似“门槛效应”;当N=2 000时，SN为3.52 mm，略超过SNP(3.2 mm)。当M=0.45、0.55时，SN增长较快，分别在N=3、N=2时SN便达到SNP(3.2 mm)，呈短时间破坏沉降特点。对不同大小M下SN与N进行曲线拟合，发现其对数函数相关性良好(见表3)，其中A、B是可能与M、桩周土体性质相关的参数。

图5 SN-N曲线Fig.5 Curves of pile-top accumulated settlement SN versus cycle number N

表3 SN-N拟合曲线参数Table 3 Parameters of fitting SN-N curves

3.1.3 桩顶循环沉降速率

定义桩顶循环沉降量差值ΔS与循环次数差值ΔN之比为桩顶循环沉降速率ρN，即ρN=ΔSN/ΔN。图6为不同M下ρN与N的关系曲线。由图6可见，ρN随N的增大而逐渐减小，存在某个循环次数N，当N超过该值，ρN趋于稳定，定义桩顶循环沉降速率ρN趋于稳定所对应的循环次数N为临界循环次数Ncr，临界循环次数Ncr随M增大呈增大趋势，ρN初始值和终值也越大，ρN变化越明显。

图6 ρN-N曲线Fig.6 Curves of ρN versus N

由图6和表4可见，当M=0.15、0.25时，ρN初始值较小，ρN随N增加而逐渐减小，达到临界循环次数Ncr后趋于平缓，SN增长也十分缓慢。当N=2 000时，SN也未达SNP(3.2 mm)；ρN分别在Ncr=382、462附近即出现稳定趋势，将其位移发展形式定义为稳定型。

表4 不同动荷载比M下位移形式Table 4 Displacement form under different dynamic load ratio M

当M=0.35时，ρN初始值适中，ρN随N的增加而逐渐减小，其衰减幅度适中，SN逐渐增大，增长幅度适中。当N=28时，达到SNP(3.2 mm)，ρN在Ncr=564时出现沉降速率稳定现象，SN增加幅度有限，当N=2 000时，SN=3.52 mm，将其位移发展形式定义为渐进型。

当M=0.45、0.55时，ρN初始值较大，并迅速衰减，循环数次N=3时便已经达到破坏值，ρN分别在Ncr=646、820附近才开始出现稳定趋势，并且较难以出现稳定趋势，将其位移发展形式定义为破坏型。

Chan等[12]在砂土中开展循环桩基试验，研究桩顶累计沉降量SN、沉降速率ρN与循环加载次数N的关系，认为循环加载会导致桩顶沉降速率变化，可根据沉降速率稳定与否，把桩的沉降划分2至3个形式：当桩顶荷载P较小时，桩处于长时间稳定阶段；P较大时,沉降速率不容易稳定。其结果与本试验现象具有一致性，工程中可根据Ncr和ρN变化趋势进行循环荷载下单桩安全稳定性评价。

3.1.4 相同荷载幅值下SP与SN曲线

图7为相同荷载幅值Pmax下SP与SN曲线，由图7可见，当荷载幅值较小时，循环加载与静载产生的桩顶累计沉降量差异不大。当Pmax超过5 kN后，SN与SP之间差异逐渐明显。定义相同荷载幅值下，SN与SP之比为动静沉降比α(α=SN/SP)，发现不同大小M下，α介于1.01～1.72之间，将α和M进行曲线拟合，拟合方程为：α=0.890 7M+0.835(R2=0.925),满足一定线性关系，工程中可尝试利用α和M，结合SP大小，预测不同大小循环荷载桩顶循环累计沉降量SN。

图7 相同荷载幅值下SP与SN曲线Fig.7 Curves of SP and SN under the same load amplitude

3.2 桩端阻力和桩侧阻力

3.2.1 静荷载桩端平均阻力qs

图8为静载时，桩端平均阻力qs随P变化曲线。由图8可见，qs随P增大而逐渐增大，荷载增量ΔP=0.5 kN相同,但qs的增长趋势却不相同，呈现出OA-AB-BC三段式发展。在OA段，P较小，qs增长幅度较小，当P=2.5 kN时，qs=2.0 MPa，SP=1.8 mm;在AB段，qs随P增大继续增加，增速略有加快，当P=6.5 kN，qs=4.2 MPa，SP=11.86 mm,SP开始逐渐明显；在BC段，当P=9 kN;qs为6.5 MPa,SP陡增至20 mm。加载BC段，qs呈直线增长变化，与静载桩顶累计沉降量SP变化有较强一致性。

图8 静荷桩端平均阻力qs随P的变化Fig.8 Variation of average resistance qs at pile tip against P under static load

3.2.2 静荷载桩侧平均摩阻力fP

图9为静载时，静载桩侧平均摩阻力fP随P变化曲线。由图9可见，荷载增量ΔP=0.5 kN相同,而fP变化趋势却不相同，fP随P增大先增大后减小。在OA段，P处于较低水平，此时fP也较小，但fP增长幅度相对较快，呈现加速增长，当P=2.5 kN时，fP=4.4 kPa，SP=1.8 mm；在AB段，fP随P增大继续增大，但增幅趋势放缓，呈减速增长，当P=9 kN时，fP=11.2 kPa，SP=11.86 mm；继续加载，当P=9.5 kN时，SP至20 mm,加载至BC阶段，fP随P增大呈减小趋势，这与qs变化具有较强互补性。

图9 静载桩侧平均摩阻力fP变化Fig.9 Variation of average friction resistance fP of pile side under static load

3.2.3 循环桩端平均阻力qNs

图10为循环加载时，不同M下循环桩端平均阻力qNs变化规律。由图10可见，qNs随N增大而逐渐增加，但不同大小M下qNs变化趋势有所不同:如图10(a)所示，当M=0.15、0.25、0.35时,qNs随N增大呈现缓慢增长的趋势，临界循环次数Ncr分别为382、462、564时，qNs开始出现弱化趋势；如图10(b)所示，当M=0.45、0.55时，qNs随N的增大，先在短时内变化较为明显，增长较快，后呈现出缓慢增长趋势，当Ncr分别为646、820时，qNs出现弱化趋势，后期qNs仅略微增大，可见qNs不会随着M增大一直增大，而会趋向稳定。

图10 循环桩端平均阻力qNs变化Fig.10 Variation of average resistance qNs at pile end under cyclic load

3.2.4 循环桩侧平均摩阻力fN

图11为循环加载时，循环桩侧平均摩阻力fN随N变化规律。由图11可见，fN随N的增大而逐渐减小，M越大，fN下降幅度越明显，且fN呈现出弱化趋势，最终趋于稳定。M大小对循环桩侧平均摩阻力初值fN=0有一定影响：当M=0.15时，fN=0为5.5 kPa；当M=0.25时fN=0=7.2 kPa,增加了1.8 kPa。当M=0.35、0.45时fN=0分别为7.52、7.56 kPa，仅有微弱幅度增长。定义循环桩侧平均摩阻力终值fN=2 000与循环桩侧平均摩阻力初始值fN=0差值与循环桩侧平均摩阻力初始值fN=0之比为循环桩侧平均摩阻力弱化系数D，如式(2)。

图11 循环桩侧平均摩阻力fNFig.11 Variation of average resistance fN of pile side under cyclic load

D=[(fN=0-fN=2 000)/fN=0]×100%。

(2)

由图12可知，当M=0.15、0.25时，循环桩侧平均摩阻力fN弱化系数D=50%、53%，衰减程度已超过50%；当M=0.35，0.45、0.55时，D分别为66%，78%、82%。弱化系数D随M的增大逐渐增大，动荷载比M较小时，fN衰减程度弱，随着M的增大，弱化越明显。将M与D利用Logistic函数进行拟合,该函数目前已广泛运用在物理、化工、生物领域，得到其拟合方程为式(3)，方程参数A1、A2、x0、p如图12中方程所示，决定系数R2=0.997。工程中可尝试利用该方式，分析循环荷载下桩侧平均摩阻力弱化程度，作为控制承载力安全的参考依据。

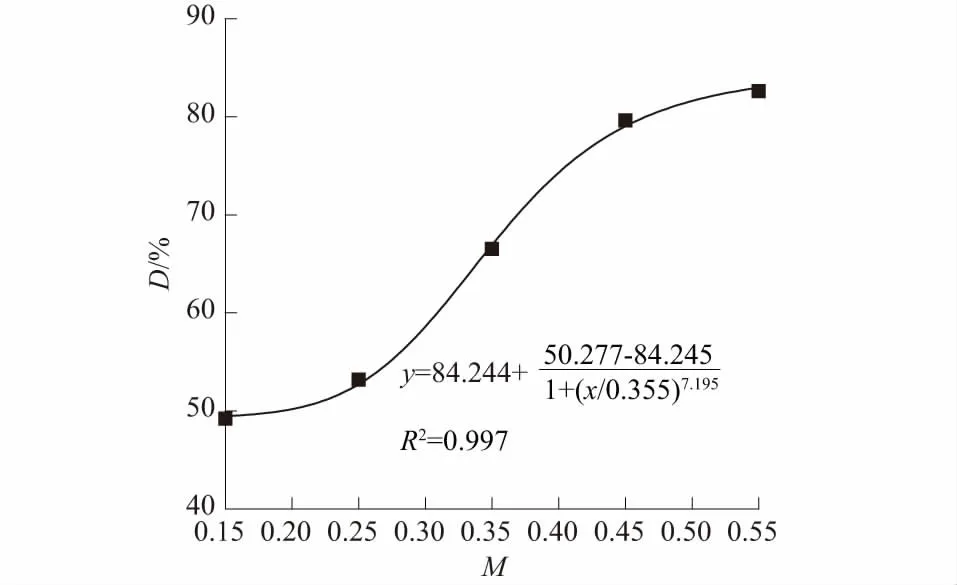
图12 动荷载比M与弱化系数D的关系Fig.12 Relationship between dynamic load ratio M and weakening coefficient D

(3)

3.2.5 桩端/桩侧承担上部荷载比例

图13为2种加载方式下桩端/桩侧分担上部荷载的比例，其中图13(a)为静荷加载下，桩端和桩侧分担荷载比例。由图13(a)可知，在静荷加载的过程中,在荷载较小时，桩侧平均摩阻力承担了大部分荷载，约占荷载比例75%，而桩端阻力承担荷载较少，约为25%。而随着荷载P增大，桩侧平均摩阻力承担的荷载比例逐渐降低，桩端阻力开始承担上部荷载，加载后期桩端平均摩阻力占荷载比例的90%，桩侧平均摩阻力仅为10%左右。

图13 静荷加载、循环加载桩端/桩侧分担荷载比例Fig.13 Load sharing ratios of pile end and pile side under static and cyclic loads

图13(b)为循环加载下，桩端和桩侧分担荷载比例，由图13(b)可知，在循环加载的过程中，桩端和桩侧分担循环荷载的比例是处于动态变化的，大体上也呈现出桩侧分担荷载比例减小、桩端分担荷载比例增大的趋势，且分担比例变化主要在循环加载前期。动荷载比对分担荷载比例的变化趋势影响明显，当动荷载比M=0.15、0.25、0.35时，桩端/桩侧分担比例为33.94%、32.48%、22.04%，呈现出递减趋势。随着动荷载比增大，M=0.45、0.55时,加载初期桩端阻力荷载比例为90%，桩侧阻力荷载比例约为10%，且随着循环加载进行，变化比例十分有限，仅为3%，可见当动荷载较大时，桩侧摩阻力会短时内充分发挥后骤降，桩端在前期需快速承担大部分荷载。

4 机理分析

4.1 桩顶累计沉降发展模式分析

4.1.1 静载桩顶累计沉降形式

桩基承载过程中，竖向荷载P由桩侧摩阻力fP和桩端阻力qs共同承担，桩侧先承载，桩端后承载。静载初期OA段，P较小，侧摩阻力fP承担大部分荷载，桩端钙质砂压缩变形量有限，SP不明显。AB段，随着P增大，fP继续增大，却不足以提供承载力，桩端逐步承载，桩端土发生压缩变形和颗粒破碎，导致桩顶沉降加剧，到BC段，当桩基承载力不足以承担上部荷载P，桩顶沉降陡增，SP呈三段式发展，试验现象与研究[14-15]一致。

4.1.2 循环桩顶累计沉降形式

循环荷载P同样由桩侧循环摩阻力fN和桩端循环摩阻力qN共同承担。循环加载中，桩端土体反复受上部循环应力作用，不断发生孔隙压密和颗粒破碎，且桩端土压缩变形主要由颗粒破碎控制[3]，桩端土体逐步压缩变形，导致桩顶循环累计沉降SN逐渐增大。颗粒破碎发生需达到相应的破碎应力[23]，当M越大，能提供的破碎应力越大，颗粒破碎程度越严重，土体压缩变形越大，桩顶循环累计沉降终值SNf也较大。当M越小，循环应力水平较低，导致颗粒破碎有限，桩端土体压缩变形有限，形成稳定型沉降。随着M增大，循环应力水平提高，桩端土颗粒破碎更严重，桩端土体变形更为严重，形成渐进型和破坏型沉降。笔者在此前动力荷载下钙质砂侧限压缩试验中发现，试样压缩变形随动载幅值增大而增大[24]，与本试验现象相一致。

循环加载时，存在一个稳定的临界循环次数Ncr，超过该加载次数时，桩顶循环沉降速率ρN出现衰减稳定现象，SN出现稳定。这是因为桩端土体受循环应力作用时，土体被压密并发生颗粒破碎。颗粒破碎形成的细小颗粒填充到土体骨架中，导致钙质砂颗粒间点-点接触增多，配位数增多，使土体有效应力面积增加，继续发生颗粒破碎需要更大的破碎应力，一定程度上抑制了颗粒破碎发生，桩顶循环沉降速率ρN出现衰减，桩端土体压缩变形出现弱化趋势。M越大，能提供的循环荷载破碎应力越大，引起颗粒破碎程度越严重，抑制颗粒破碎发生和减弱桩端土体压缩变形越困难，临界循环次数Ncr越大。

4.1.3 动静沉降比

相同荷载幅值下，动静沉降比α(SN/SP)>1，因为桩端土受静载时处于静态受迫压缩变形，颗粒压缩变形和颗粒破碎有限，而循环加载时，桩土间反复发生颗粒压密和局部应力集中，导致更多钙质砂发生颗粒破碎，循环加载的振扰使得破碎形成的细小颗粒更易填充至颗粒骨架中，共同加速桩端土体压缩变形，笔者在动力类型荷载下钙质砂侧限压缩试验中也发现类似现象[24]。

4.2 桩端/桩侧承担荷载变化

4.2.1 静荷承载

当静荷载P较小时，桩侧摩阻力fP提供承载，且fP尚未完全发挥，fP承担上部荷载过程中，桩侧的桩土间相对位移趋势愈来愈强，导致fP增幅较快；在加载中期AB段，随P增大，fP不足以承担上部荷载，桩端平均阻力qs开始承载，桩端土受压开始更明显，qs增幅加快，桩侧土的剪切位移导致桩侧土体颗粒破碎，使桩侧土产生应力松弛现象，fP增幅减缓；加载至BC段，qs和fP共同承担荷载P，且以桩端承载为主，qs增幅继续加大，当P超过至桩基极限承载力Qc，桩顶发生瞬时沉降，桩侧土体颗粒破碎较为严重，fP开始减小，同时qs加速增长。

4.2.2 循环承载

如图14所示，在循环加载中，钙质砂单桩累计沉降机理也遵循桩侧先承载、桩端后承载的规律。与静载相比，随着循环加载进行，循环加载下将出现反复应力集中现象，桩侧钙质砂在桩土接触界面发生的反复剪切，致使桩侧土体颗粒破碎产生的“累计损伤”效果，导致桩侧土体应力松弛，削弱桩侧承载能力，fN逐渐减小，桩端钙质砂发生压密和受压颗粒破碎，qNs缓慢增大。M越大所造成的桩侧土体剪切变形越严重，所形成的应力松弛现象越明显，因而fN降低幅度越大，qNs增幅越大。颗粒破碎后，桩侧呈现出应力松弛，形成的细小颗粒填充到土体骨架内，增大土体有效应力面积，继续发生颗粒破碎更加困难，桩侧摩阻力弱化趋势逐渐减弱。

图14 钙质砂单桩累计沉降机理示意图Fig.14 Schematic diagram of accumulated settlement mechanism of single pile in calcareous sand

5 工程实用意义

珊瑚礁施工中，动荷载比M对于桩顶沉降形式和承载特性具有实际意义。在不同M值下，桩顶沉降形式有稳定型、渐进型、破坏型3类，本试验中动荷载比M应<0.35，可确保桩基沉降为稳定型，根据M和Qc可预测桩顶沉降发展形式。根据桩顶循环沉降速率ρN的变化趋势，分析临界循环次数Ncr，预测桩基础在动力循环下的沉降稳定区间。桩基础设计施工中，应重点考虑环境中动荷载比M大小,经济安全地服务于钙质砂区域工程建设。

利用动静沉降比α与M存在的线性相关性，采用雨流法[22]等统计方法进行荷载效应等效，根据静载时桩顶累计沉降SP预测同荷载幅值下的循环荷载桩顶循环累计沉降SN，从而服务工程建设。循环荷载对钙质砂桩基桩侧摩阻力存在弱化效应，引起桩端与桩侧承载能力的变化。工程中可以通过埋设土压力盒监测桩端阻力qNs变化，分析监测循环荷载下桩基沉降稳定性，可使用本试验中得出的M与弱化系数D之间存在的函数关系式，预测循环荷载下钙质砂单桩桩侧平均摩阻力弱化程度，作为设计桩基承载力安全系数的参考依据。

6 结 论

(1)SN随N增大而逐渐增大，SN-N曲线可采用对数函数进行描述，动荷载比M越大，桩顶累计沉降终值SNf越大，单桩沉降形式主要有稳定型、渐进型、破坏型3种，有显著“门槛效应”，达到临界循环次数Ncr时，桩顶循环沉降速率ρN出现衰减稳定现象，试验中M安全临界区间为0.35～0.45。

(2)静载时，桩顶累计沉降SP、桩端平均阻力qs、桩侧平均摩阻力fP的发展均表现为三段式，SP和qs逐渐加速增长，fP先增长后减小。循环加载时，桩侧摩阻力fN逐渐减小，循环桩端平均阻力qNs缓慢增大。M越大，桩侧摩阻力fN降低幅度越大，动荷载比M与弱化系数D存在Logistic函数关系。

(3)动静沉降比α(SN与SP之比)介于1.01～1.79之间，且α与M满足一定线性相关性，工程中可工程可尝试利用α和M，结合SP大小，预测同等大小循环荷载作用下桩顶循环累计沉降SN。

(4)岛礁桩基工程设计应考虑控制动荷载比M大小，确保桩基使用安全。可利用动荷载比M与弱化系数D、动静沉降比α、循环沉降速率ρN等作为循环荷载作用下桩基设计和承载参考依据。