基于均匀设计-响应面-有限元法的软岩隧洞围岩与衬砌结构协同承载可靠性分析

张 肃，丁秀丽，黄书岭

(长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

近年来，为了解决我国水资源时空分布严重不均的问题，一批以长距离输水隧洞为主要输水建筑物的隧洞工程纷纷兴建，大埋深、复杂地质条件下的隧洞工程设计与施工成为工程建设中的难点，特别是穿越高地应力区的软岩隧洞工程，极低强度应力比导致的围岩大变形给隧洞衬砌设计带来了极大的挑战。传统的结构安全设计方法在面临随机变量复杂、函数不能显式表达的问题时具有较大的局限性，基于数理统计理论的可靠度计算方法可以更全面地评价隧洞工程中的安全性，为工程的前期决策、施工过程、后期维护提供有力的科学依据。

20世纪80年代末期，国内学者就对可靠度理论在隧洞工程的应用展开了研究，例如景诗庭[1]在稳定性分析的基础上，提出了利用模糊概率计算地下坑道的可靠度；谢锦昌[2]结合“荷载-结构”模型对铁路隧洞衬砌的可靠性进行了研究；在近几年的研究中，周泽林等[3]对深埋软岩隧洞的软弱围岩的支护结构进行了受力分析和安全性评价；湖南大学的梁斌[4]在围岩与支护协同承载理论的基础上建立了运用一维直接积分求解可靠度的方法；浙江大学的肖志鹏[5]根据支护-围岩相互作用的机理提出了隧洞开挖的可靠度计算优化方法等等。不同的隧洞结构可靠度计算方法陆续提出，意味着可靠度理论在隧洞工程领域的应用进一步深化。

对于修建在IV、V类岩体中的隧洞，特别是软岩隧洞，通常需要围岩和支护系统形成一个整体共同承受开挖释放的荷载[6]，以此维护隧洞的稳定性。因此，如何合理评价软岩隧洞围岩和衬砌结构协同承载的可靠性以保障支护结构的安全成为一项重要工作。现有的基于蒙特卡洛原理的随机有限元是结构可靠性分析常用方法，但该方法计算量大，计算效率低；以当量正态化(JC)法为代表的传统可靠度计算方法则依赖于功能函数的显式表达，而地下工程随机变量的复杂性和模糊性，难以像地面结构一样从理论上构建功能函数的显式表达，成为在隧洞工程应用中的制约因素。为此，在可靠度计算理论基础上，本文将均匀设计方法、响应面法和有限元数值模拟方法相结合，利用《水工隧洞设计规范》(SL 279—2016)[7]中衬砌结构的承载力极限状态函数，建立围岩和衬砌结构协同承载的荷载效应响应面显式表达式，提出一种软岩隧洞围岩和衬砌结构协同承载可靠性评价方法，以达到满足计算精度且提高计算效率的目的，有助于解决软岩隧洞围岩和衬砌结构联合承载时可靠性评价的问题。

2 软岩隧洞围岩和衬砌结构协同承载的可靠性评价方法

2.1 试验方案的均匀设计方法

作为一种统计设计方法，均匀设计法考虑的是试验点在整体数据样本内“均匀分散”的情况。这些试验点因其代表性而可以减少设计试验所需的次数[8]。

能否在整体数据样本内确定有效的试验点是试验设计决定性因素，进行试验设计的最终目标就是利用尽可能少的试验得到系统内最为充分和具代表性的信息。均匀设计法利用了试验点在样本范围内均匀分散的特点，能够较好地实现上述目标，尤其适用于多因素水平的试验设计。通过对随机变量在其取值范围内等间隔均匀取值，依照对应因素与水平数的均匀试验表获取试验点的数据组合，便可获得合理高效的数值试验方案。尤其是对于多元非线性的数据样本，均匀设计法在使用上有明显的优势。

例如当试验中有n个因素，每个因素有m个水平，全面设计和正交设计都需要大量的试验次数，而均匀设计只需要m次试验，大大降低了计算成本。均匀设计法的使用需要配合对应因素和水平数的均匀设计表，表中的均匀设计符号Un(qs) 的示意见图1。

图1 均匀设计符号 示意图Fig.1 Schematic diagram of uniform design symbols

值得注意的是，均匀设计体现的是试验点的分散而非整齐分布，方差分析法因此并不适用，而应采用回归分析的方法。

均匀设计-响应面-有限元响应面法进行数值试验之前首先需要科学合理地设计试验方法，而隧洞围岩与衬砌结构协同承载的可靠度问题本身就是一个多因子影响下的高度非线性问题，其功能函数从理论上无法显式表达。因此可以通过均匀试验法合理高效地设计数值试验方案，进而拟合出函数模型。

2.2 可靠度计算的响应面方法

作为一种可靠度计算方法，响应面法的核心思想是通过响应面函数拟合出明确的函数关系[9]，从而将结构中难以求得的真实功能函数进行显示表达。

假设结构的功能函数中含有相互独立的随机变量Xi(i=1,2,…,n)，结构中真实的功能函数可用Z=G(Xi)表示,但该功能函数难以从理论上求出准确的表达式。设响应面函数Z=g(Xi)，同样含有随机变量Xi(i=1,2,…,n)。原功能函数与响应面函数曲面的关系可用图2表示。

图2 响应面函数与原功能函数曲面的关系Fig.2 Relationship between response surface and real function surface

在拟合响应面的各种方法中，响应面法的二次响应函数运用已十分广泛[10]，该方法用纯二次函数的形式拟合结构中的真实功能函数Z,即

(1)

(2)

式中:mXi为Xi的平均值;σXi为Xi的标准差。则极限状态方程可以通过标准正态化之后的变量表示为

(3)

(4)

坐标系变换时其方向余弦相同，可以代入式(2)得到设计验算点P*在原坐标下的表达式,即

(5)

鉴于点P*位于极限状态曲面上，故满足

(6)

(7)

(8)

式中:F(x)为概应分布函数；f(x)为概率密度函数。

从而可以将非正态分布的随机变量当量正态，再代入式(2)—式(6)即可求解可靠度指标。

2.3 围岩和衬砌结构协同承载的可靠性评价方法及流程

软岩隧洞的围岩和支护系统协同承载理论有机地将支护结构与围岩联系起来，将二者视为一个整体。在系统中，围岩单元既承接变形，同时也施加荷载，作用在围岩上的支护系统约束和限制了围岩向隧洞内变形，承受了形变压力，相应分担了部分荷载；同时，支护系统的加固作用也使围岩自承载的能力得以充分发挥，这充分体现了围岩和支护系统相互作用的原理。

软岩隧洞的围岩和支护系统协同承载维护了围岩的稳定以及衬砌结构的安全，是当今地下工程主流的设计理念[12]。因此，对软岩隧洞围岩和衬砌结构协同承载的可靠性进行评价是一项重要课题。基于蒙特卡洛原理的随机有限元是结构可靠度计算的常用方法，但其计算效率不高的缺陷制约了发展。

由于隧洞工程赋存地质环境的隐蔽性和复杂性以及支护系统的多样性，由围岩和支护系统构成的地下结构真实的功能函数难以从理论上显式表达，近年来发展起来的响应面法由于能够通过显式表达式给出结构体的真实极限状态，具有广泛的应用前景。响应面法的运用需要足够多的数据试验样本，才能拟合出结构的真实极限状态的功能函数[13]。为减少试验所需的次数，提高计算效率并保证计算精度，将均匀设计方法和响应面法相结合，通过建立围岩与衬砌协同承载下的数值仿真模型，利用《水工隧洞设计规范》(SL 279—2016)(以下简称《规范》)中的相关函数和推荐取值，实现在有限的数据条件下拟合出真实极限状态的功能函数，由此建立围岩和衬砌结构协同承载的荷载效应响应面显式表达式。

在可靠度理论中，极限状态方程可以表达为

Z=R-S。

(9)

式中:Z为结构功能函数;S为荷载效应函数;R为结构抗力函数。结合式(9)，并根据《规范》中衬砌结构的承载力极限状态函数，可表达出依照响应面法的围岩与衬砌结构协同承载功能函数(极限状态方程)的表达式，即

Z=R(fd,αk)-γdγ0ψS(·)。

(10)

式中:γ0指结构重要性系数，Ⅰ级结构、Ⅱ级结构、Ⅲ级结构分别按照对应的安全等级取1.1、1.0、0.9；ψ为状况设计系数，按照对应工况分别取值1.0、0.95、0.85；R为支护的抗力函数;γd为结构系数，按支护类型选用；fd为材料抗压强度；αk为几何参数;S(·)为荷载效应函数。

通过均匀设计响应面法对S(·)的表达式进行拟合，进而求出可靠度指标以及失效概率，评价围岩和衬砌结构协同承载的可靠性。下面给出围岩和衬砌结构协同承载可靠性评价的具体实施流程，如图3所示。

图3 围岩和衬砌结构协同承载可靠性评价方法和流程Fig.3 Flowchart of reliability evaluation of the collabora- tive bearing of surrounding rock and lining structure

(1)建立基于围岩与衬砌结构协同承载理论的有限元数值模型，计算和分析在单一变量影响下结构中应力分布的变化规律，从而确定拟合响应面函数所需要的随机变量。

(2)设计一个多元响应面函数，自变量为与结构荷载有关的相互独立的随机变量(X1，X2，X3，…)，因变量为响应值S，要求设计函数与真实函数尽可能接近且形式尽可能简单。

(3)依照均匀设计法进行试验组合方案设计，各变量在取值范围内均匀间隔取值后依照相对应因素和水平数的均匀设计表组合成一个试验点矩阵如[X11，X21，X31，…]，根据试验设计方法规则确定一系列的试验点称设计矩阵[D]=[Xmn]，后进行数值试验对应得出一系列响应值[S]。

(4)根据上述步骤得到的结果进行回归分析，确定拟合函数中各项待定系数，给出响应面函数的显式表达，代入功能函数Z得到极限状态函数的显式表达式。

(5)采用概率论和JC法，得到可靠度指标和失效概率。具体为：假设一个验算点P*取其坐标值xi*(一般均值mxi*)，将其当量正态化，代入式(3)—式(6)求出β；按β值与式(5)反解验算点坐标，根据新的验算点重复以上步骤，直到两次β值的误差不大于允许误差，既求出了可靠度指标β，相应地得到失效概率Pf。根据获得的可靠度，对围岩和衬砌结构协同承载可靠性进行评价。

3 围岩和衬砌结构联合承载可靠性的单因素随机变量分析

为了确定响应面函数中所包含的单因素随机变量，以某深埋软岩圆形隧洞为例，建立考虑围岩与衬砌协同承载的有限元计算模型进行数值模拟计算[14],同时选取各材料的本构模型和单元类型。

隧洞开挖以及复合衬砌施作的相对流程可通过有限元计算程序中的生死单元进行控制。考虑围岩的自重应力场与构造应力场，其中水平侧压系数取1.1。计算模型对两侧面的约束方向为法向，底面约束方向为法向与切向。计算模型的网格划分与边界条件如图4所示。计算模型在x和y方向的边界为100 m，开挖洞径10.8 m，初衬厚度0.2 m，二次衬砌厚度0.5 m，衬后内径9.4 m，其余材料参数如表1所示。

图4 计算模型网格与边界条件Fig.4 Computational meshes and boundary conditions

表1 各材料本构模型和单元类型Table 1 Constitutive model and element type of each material

在600 m埋深90%荷载释放率的工况下，按照控制其余因变量不变保持单一影响因子的原则，分别计算围岩与衬砌有关参数对二次衬砌环向轴应力的影响(见图5、图6)。在衬砌与围岩协同承载的前提下，围岩参数和衬砌参数的变化会共同影响结构的受力特征。可靠度计算应在对衬砌应力状态分析的基础上从影响因子中选取拟合响应面函数所需要的基本随机变量。

图5 衬砌截面轴应力随围岩变形参数和强度参数的 变化规律Fig.5 Variation of axial stress of lining section with deformation and strength parameters of surrounding rock

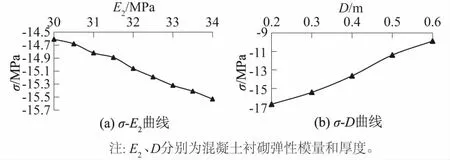
图6 衬砌截面轴应力随混凝土衬砌弹性模量和 厚度的变化规律Fig.6 Variation of axial stress of lining section with elastic modulus and thickness of concrete lining

由于对某个确定的隧洞结构断面进行结构计算时，其埋深、施工荷载释放率以及水荷载等外环境均已经确定；围岩参数E1、φ、c与衬砌参数E2、D作为计算模型内部“影响因子”客观上存在着显著的随机性，主要由于实际工程中监测技术、参数反演方法中存在的差异性。衬砌厚度D虽然具备以上特征，但实际中其变化幅度的数量级远小于其他参数，故忽略其随机性带来的影响。因此，确定衬砌可靠度计算所需的随机变量，可从E1、φ、c、E2四个参数作为主要影响因子中选取，具体还需依据实际工程特点作取舍。

4 工程应用

阳江核电站冷却水排水隧洞中风化花岗岩斑岩洞段为IV类岩体，通过基于均匀设计-响应面-有限元法的可靠度计算方法，获得可靠度指标β以及失效概率Pf，对排水隧洞围岩和衬砌结构协同承载的结构可靠性进行评价。

该洞段外压水头19.246 m，影响较小，实际计算时可不予考虑。模型建立过程如上文所述，侧压系数取0.9，荷载释放率取90%，模型范围80 m×80 m，二衬混凝土内径6.7 m，厚度为0.4 m。按照上文选定的围岩的变形模量E1、内摩擦角φ、黏聚力c以及衬砌弹性模量E2这4个因变量为影响结构功能函数的随机变量。材料各参数值参考实测结果取值，如表2和表3所示，混凝土力学参数见表4。

表2 材料参数Table 2 Material parameters

表3 阳江核电站冷却排水隧洞Ⅳ类围岩参数Table 3 Parameters of class Ⅳ surrounding rock of cooling and drainage tunnel of Yangjiang Nuclear Power Station

表4 混凝土力学参数Table 4 Mechanical parameters of concrete

依据均匀设计法“均匀分散”的原则在上述取值范围内等间隔取值，参照4因素9水平均匀设计表设计试验点的数据组合，见表5。

表5 4因素9水平均匀设计表Table 5 Uniform design table with four factors and nine levels

在考虑单一影响因子的计算中，发现各随机变量与衬砌轴应力呈线性或二次曲线的相关关系，故选用纯二次多项式(Pure Quadratic)以及线性多项式(Liner)来拟合其真实函数(式(11))，对比两种影响面函数模型的显著性。

(11)

本工况下衬砌的主要破坏模式为受压破坏，本文认为当衬砌内某一点发生破坏时结构即面临失效，故选取衬砌典型截面最大轴应力σ为响应面函数的响应值。依照均匀设计方法设计试验并通过有限元计算程序模拟，计算结果见表6。

表6 各试验点在最危险截面轴应力计算结果Table 6 Calculation results of axial stress at the most dangerous section of each test point

采用拟合的方法，得到二次多项式中的各项系数，并代入式(11)中得到

σ=-59 485.6-25.925 1E1-61.495 3E2-37 512c+

62 632.33c2-66.664 2φ2。

(12)

拟合模型的剩余标准差值越接近于0，显著性越好。该计算模型的剩余标准差RMSE=1.177 3，表明该模型显著性良好。

对于Liner函数拟合的线性多项式，得到其拟合函数为

σ=-20.578 9+0.733 0E1-0.426 1E2+

17.058 1c+0.142 6φ。

(13)

线性多项式的剩余标准差RMSE=2.553 3，大于纯二次多项式拟合得到的剩余标准差RMSE=1.177 3，后者的显著性更好。考虑到当待定系数增加时，试验的计算量会增加。纯二次多项式的拟合模型显著性良好，且试验次数相对较少，具有可行性。

根据承载力极限状态函数，并赋予αk相应的几何参数，衬砌厚度D与宽度h分别取值0.4 m与1 m，根据工程经验，γ0、ψ、γd分别取值1.0、1.0、0.9。参考C35混凝土与Ⅳ级围岩的相关规定参数，得到相关随机变量的统计学特征，见表7。

表7 各随机变量统计特征Table 7 Statistical characteristics of each random variable

将以上参数值代入前文拟合出的响应面函数，得到荷载效应S(衬砌典型截面环向轴应力σ最大值)的统计分布，见表8。

表8 均匀试验下荷载统计特征参数Table 8 Statistical characteristic parameters of load under uniform test

最后按照JC法在MatLab中编制相应的计算程序，将有关参数代入，得到按衬砌承载力抗压极限状态计算的可靠度指标β=3.684以及失效概率Pf=0.000 16，与基于蒙特卡洛的随机有限元可靠度计算结果β=3.8、Pf=0.000 4相比较[15]，两者可靠度指标相差在3%左右，失效概率相差较大。本文认为其主要与不同计算模式下可靠度指标与失效概率的对应关系有关，且可靠度指标较高时，较小的可靠度指标差异会使得失效概率发生较大的变化。总体而言，对于相应《规范》的要求，本工程获得的可靠度指标β为3.684，表明隧洞衬砌结构安全性是可靠有保障的。

5 结 论

本文在可靠度计算理论的基础上，将均匀设计方法、响应面法和有限元数值模拟方法相结合，利用《水工隧洞设计规范》(SL 279—2016)中衬砌结构的承载力极限状态函数，构建了围岩和衬砌结构协同承载的荷载效应响应面显式表达式，提出一种软岩隧洞围岩和衬砌结构协同承载可靠度计算方法。在此基础上，建立了围岩与衬砌协同承载数值计算模型，分析了影响围岩和衬砌结构联合承载特性的单因素随机变量，辨识了影响围岩和衬砌结构联合承载可靠性的主要因素，包括围岩的变形模量、黏聚力和内摩擦角以及衬砌的弹性模量等。

将上述方法应用到具体工程中，检验了该方法的可靠性，同时与传统可靠度计算方法进行了对比，结果表明所提出的方法具有很好的适应性和可行性，且在保证计算精度的前提下，简化了计算流程，使计算更为高效，有助于解决水工软岩隧洞围岩和衬砌结构联合承载时的可靠性评价和应用的问题。