天课时分配下的多阶段新高考走班制排课算法

张宇瞳，刘 静，郝星星

西安电子科技大学 人工智能学院，西安710071

新高考改革的政策已经逐步在全国范围内实施，各个省份推出了适合自己的教学与考试变革方案。新高考改革的一个特点在于学生的考试科目不再是从文科与理科考试科目集合中“二选一”，而是根据自身喜好特长和所在学校特色以及目标报考大学专业要求选择自己的考试科目组合，通常为“6选3”或“7选3”[1-2]。考试科目组合的变化将带来教学组织的变化，核心体现为同一个行政班的学生可能存在的选课组合增多。通常来说不适合将学生需要上的所有科目安排在一个行政班内开设，而解决这一问题的常见方案为走班制教学[1-4]。在走班制教学中，学生将根据选课与分班结果在自己所属行政班不上课的时段内到某个教学班上自己所选的选修科目。这一教学组织模式为教务排课工作带来诸多新的挑战，比如大量教学班的出现、学生上课冲突的出现等，这些都是学生个性化选择与学校统筹安排和教学秩序管理之间新出现的矛盾[2]。

本文主要解决的问题是“新高改”模式下高中走班制排课中如何提高排出的课表对老师教案平齐的满足程度、课时分布均匀程度以及对同时上课要求的满足程度。老师教案平齐和课时分布均匀程度是诸多学校结合本校老师的教学经验和学生学习效果总结出的两条较为重要的课表质量评价指标。因此在走班制教学过程中这些学校也希望排出的课表能在这两条指标上有较高的满足程度。但不可否认相较于仅有行政班课表的排课任务，走班排课过程中可行课表的搜索难度提高了，优化其他目标的难度也明显增大。这里所说的可行课表指的是课表中每一门科目课时均满足预先设定的一周课时总量并且不能出现学生和老师的上课时间冲突。为了最大程度利用上课时间，许多学校在排课过程中指定了在某个时间段内行政班都不上课而只有走班在上课，这样就得出一种名为“同时上课”的课表要求。在走班制课表排布过程中同时上课规则不仅是对课表的一项新增要求，通过本文的案例实验研究也发现设置合理的同时上课规则也有助于优化算法尽快排出高质量的课表。

为此，提出一种多阶段新高考“走班”排课算法，将排课过程划分为“优化教学班课表课时分配”“优化获得教学班完整课表”“优化行政班课表课时分配”“优化获得行政班完整课表”四个阶段。其中两个课时分配阶段是本文提出算法中的核心阶段。在对大量学校的课表进行观测后发现一个优良的课表首先得是一个课时分布合理的课表。通过对学校真实排课过程的观摩，发现通常来说跨天转移一个班级的某门课程的课时是一个较为困难的过程，通过算法自动生成的课表如果可以避免天之间的课时转移将对后续人工调课大有裨益。因此将待优化课表中每个班每一科目的天课时分配放在首要位置，设计了一个多阶段的排课算法。在天课时分配优化阶段可以就教案平齐违反、课时分布不均匀等目标函数最小化进行课表优化。然后在下一阶段中，将课表变化的范围锁定在一天之内，就课时优选、行政班可用空闲时段最大等目标进行优化，称这一阶段为“天内课表优化”。整个过程先从单独排教学班课表开始，在得到不违反约束条件的教学班课表之后继续分配行政班课时并最终得到完整课表。

在多阶段排课算法中，设计了5个目标函数：（1）满足课时均匀的教案平齐；（2）同时上课课时一致；（3）可排出不冲突课表的课时分配；（4）教学班课时占用压缩；（5）满足行政班可用排课时段。前四个目标函数用于教学班和行政班的天课时分配优化阶段，第五个目标函数用于教学班的天内课表优化阶段。除此之外还沿用了已有研究中的学生或老师的课时不出现冲突的约束条件[5-6]用于获得可行课表以及课时优选目标函数[5，7]用于获得更为接近实用的课表。提出了一种可以解决约束优化问题的改进爬山算法用于天课时分配优化阶段。针对跨天调整课时需要调整多张课表的特点，为该阶段使用的爬山算法设计了无评价均匀分布算子、同时上课修正和转移算子以及不可排课情况下的教学班课时转移算子。

为了验证本文提出算法的有效性，选用了三个不同难度和规模的排课案例。对最终输出课表各项指标的满足情况进行了进一步细分观察。在三个案例上本文提出算法均可以以85%以上的概率排出可行课表，整个过程的计算时间消耗也在可接受范围内。在人工生成案例上的实验结果说明了算法可以在教案平齐、课时分布、行政班课时满足等目标函数上达到全局最优。教学班课表教案平齐指标满足较行政班而言更为理想，整体课表的教案平齐满足与行政班课表的教案平齐满足呈正相关。通过进一步实验还发现，教学班同时上课规则的出现对其他规则的满足具有优化指导作用。

1 相关工作与研究动机

自2014年教育部颁布《关于普通高中学业水平考试的实施意见》以来，对高中走班制排课算法的研究逐渐受到关注[4]。走班制的做法与高校的授课方法较为接近，都要求学生根据自己所选课程的安排于指定时间到指定教室上课。二者之间的主要差别在于学生的选课对排课的影响。通常来说高校排课都是发生在学生选课之前，高中走班制排课则是在学生选课之后，并且有一个根据学生高考选考科目的不同划分所在行政班和教学班的过程[8]。因此已有的中学或高校的排课模式均不适用于中学走班制教学排课任务。

王卫红等人[5]提出了一种改进的遗传算法解决高中走班制排课问题，以对学生进行分组的方式划分出多个教学班组并以组为单位制定不同课表。李文琼[9]在其研究中就文献[5]中的模型和算法进行了进一步的说明和实验分析。董玉锁等人[10]同样使用改进遗传算法解决走班制排课问题，并且定义了三种排课约束，将这一问题建模为约束优化问题。吴小芳[11]在其文章中使用分包策略将所有教学班的上课时间分在三个时间段并且将学生根据选课组合进行分组和分配包，有效地化解了学生之间的课时冲突问题。陈璐等人[7]使用两次遗传算法对走班课程和非走班课程进行了分阶段排课。在对一个年级当中的所有班级进行分组后将组内相同课程安排在同一时间。Hao等人[6]采用两阶段模拟退火算法解决高中走班制排课问题。在该文中提出的模型兼容了更为自由的学生分班方式。

排课问题在国际学术圈是一个经久不衰的研究热点。近些年先后出现延迟接受爬山方法[12]、整数规划方法[13]、融合迭代搜索和变邻域搜索（Variable Neighborhood Search，VNS）方法[14]、并行局部搜索方法[15]以及融合列生成和并行元启发方法[16]来解决高中排课问题。这些研究当中的问题背景多为传统的高中排课，涉及数学模型不够贴近实用，目前看来不能直接适配中国的高中走班排课应用中，但本文优化算法的设计受到这些优化搜索策略的启发。

回顾这些已有研究发现大部分排课方法都是基于遗传算法或启发式方法。这些方法在解决新出现的复杂优化问题上表现出较为出色的适应能力。然而各项研究仍处于初步阶段，仅对简单的约束条件和目标函数进行了数学建模。虽然部分排课方法可以将学生上课时间冲突在建模阶段消除，但要求整合自己的分班方式或分组方式[7，11]，弊端在于降低了学校个性化的操作空间。因此本文选取和文献[6]相同的学生选课数据即已分班学生数据进行研究，并且就已有研究中少有提及的教案平齐、同时上课满足、可排出不冲突课表等目标和约束条件进行建模和优化。

分组或分阶段优化方法在课表排布研究中已有应用。王祜民和赵致格[17]针对高校排课问题提出分组优化方法对难排课程优先排课。吕远方[18]使用分阶段方法分别处理高校排课中的时间表排布和教室安排表排布以减轻整体排课决策变量过多的压力。受上述研究启发，本文提出的方法将课程时间表排布分解为天课时分配和天内排课两个阶段并且根据普遍规律先排难度较大的教学班课表。

2 高中走班制排课问题的数学模型

2.1 课表基本元素

首先给出课表的数学表达。定义行政班集合为S_adm，教学班集合为S_edu。一周中某一上课天表示为d，集合为Day，一天当中的时段数记为d(slots)，一周时段总数记为。学生选课和分班过程以及教室安排过程不在本文的讨论范围内。对于排课中的几个要素：学生、课程班、老师和时段，本文对其进行如下定义、表示和取值限制。

学生被指定在若干班级内（包括一个行政班和若干教学班），这些班级开设的所有科目的所有课时学生都不能缺席。学生同一时间不能出现在两个班级内上课是学生课时不冲突的基本含义。在排课过程中真正起到影响作用的是学生的选课模式[6]而非具体某个学生，例如10个来自同一个行政班的学生选择了相同的科目并被分配在相同的教学班当中，则这10个学生可以用一个模式来替代。

课程班指的是具体某个班级的某一科目，是每个班级的基本构成之一。课程班具有所属班级、科目、层级和课时四个属性。本文中所属班级、科目和层级用于区分不同课程班，当两个课程班在这三个属性中有任何不同时即被视为不同的课程班。课程班的课时要求为该班课表一周之内安排该科目指定数目的课时，同一个班级的多个课程班的课时不能重叠。本文的课表优化中不需要限定班级或课程分组，当然也支持将分组作为一种目标函数，即同时上课规则，融入到优化过程当中。关于同时上课规则或分组对于排课优化的影响将在下文中细致讨论。

（1）这里用CClassac表示一个班级a的课程班(a∈S_adm⋃S_edu)。

（2）所有课程班的集合表示为S_CC。

（3）CClassac(slots,total)表示这个课程班一周应开设的课时数，是一个大于0的整数。

（4）CClassac(slots,t,d)表示课表t中这个课程班在d这天开设的课时数，是一个非负整数。

老师被指定带若干课程班。一个老师可能带同一个班的多门不同科目。一个老师带的不同班的同一科目或不同班级的不同科目上课时段有重叠会引起老师的上课时间冲突。

时段是课表的一个自然属性，也就是通常见到的一张课程表中去除科目后剩下的“格子”。课程班的课时将被安排于这些时段中。对于任意一个班级而言，其各课程班课时总和可能小于一周总上课时段数，剩余位置由不排课时段或空闲时段表示。对于任意一天，每个班的所有课程班课时相加不能超过这天时段数。

图1 学生选课模式，课程班，老师对应关系

图1给出了学生选课模式、课程班、老师之间的对应关系示例。一个学生选课模式对应多个课程班，一个课程班可用包含多个学生选课模式，每个课程班必须与至少一个学生选课模式相对应；一个老师可以带若干课程班，一个课程班由且只由一个老师来带。

2.2 目标函数

用于课时分配阶段的优化目标和约束条件有：满足课时均匀的教案平齐、同时上课课时一致、分配课时可以排出不冲突课表、教学班课时占用压缩。用于天内课表优化阶段的优化目标和约束条件有：行政班可用排课时段足够、课时优选、上课时间不冲突。上课课时不冲突这一约束条件的测算沿用文献[6]的方法，本文不再做出说明，这里将课表中存在的课时冲突程度记为Slot sConflict。接下来将详细介绍其余优化目标和约束条件的计算方式以及设计用意。

2.2.1 满足课时均匀的教案平齐

此目标需考虑两个因素——课时均匀分布和教案平齐。课时均匀分布要求课程班在每天当中的课时均匀分布。教案平齐要求能够确保老师所带同一科目的各课程班保持进度相同，减少一天之内需要准备的教案数量，一定程度上减轻了老师的备课负担。从课时分配的角度来对教案平齐进行描述，将其与课时均匀分布相结合，期望实现同时从老师和学生的角度优化课时分布。

在计算课时分布均匀程度之前需要事先确定每个课程班应有的课时理想分布，CClassac(slots,ideal)。这是一个长度为一周上课天数|Day|的非负整数向量，产生方式是初始化向量的每一位为，然后再为前CClassac(slot s,total)mod|Day|位加1，最终构成一个所有元素求和后等于CClassac(slots,total)并且非增序排列的向量，使用如下公式计算课时分布均匀不满足程度ide：

公式（1）中sortdecrease表示将集合A中的所有元素从大到小排序并构成一个一维向量，该公式将各课程班的各天开设的课时数与理想分布向量的欧氏距离求平方和作为目标函数。为兼容课时分布的多样性，这里特别对课时分布向量进行了排序。

一个老师所带的课程班可以分为若干个互斥非空集合，使用TeacT(p_g,k)表示教师T的第k“教案组课程班集合”（下文中用“教案组”指代）。同一个教案组的课程班科目和课时相同。教案平齐要求分为周教案平齐（表示为TeacT(p_g,k).r=w）和日教案平齐（表示为TeacT(p_g,k).r=d）两种模式，老师需要事先指定自己某个教案组要求的教案平齐模式，对于每个成员一周课时数大于天数的教案组统一采用日教案平齐方式来优化。教案平齐的违反程度vio计算如公式（2）所示：

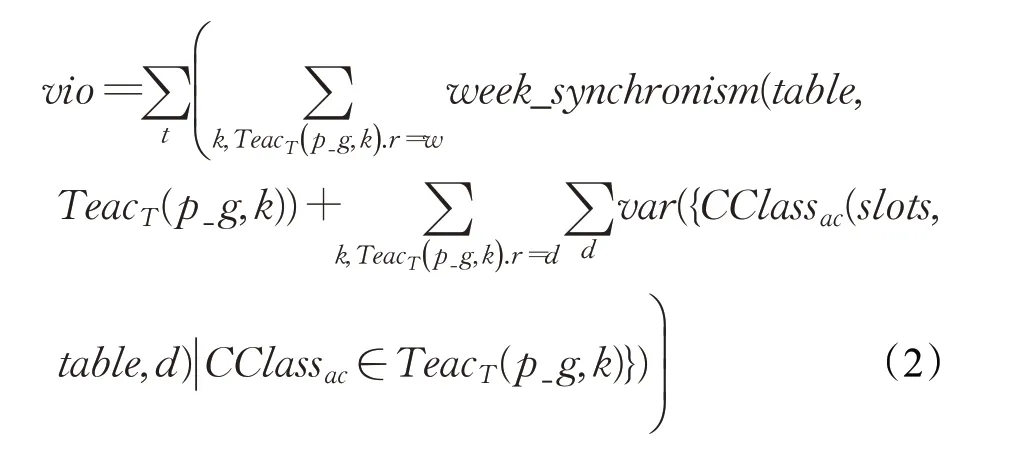
在公式（2）中，week_synchronism(a,b)表示对课表a而言教案组b的周教案平齐满足程度。var(a)表示集合a所有元素之间的整数偏差值，这里需要度量的是教案组各课程班每天课时之间的差异。满足周教案平齐的课时分布是：可以将一周上课天划分为若干区间，每个区间内只有一天上课而且所上课时数相同；满足日教案平齐的课时分布是：每天各个课程班具有相同的课时。

满足课时均匀的教案平齐这个目标为两个部分的加权和：

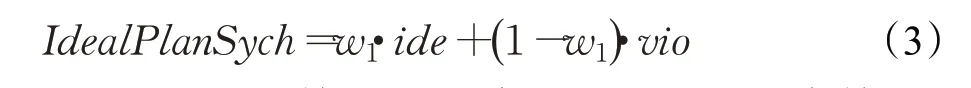
其中，w1为权重系数，为一个介于0到1之间的实数。

2.2.2 同时上课课时一致

在走班制课表排布过程中学校为避免部分学生单独上自习带来的管理问题，同时也为了提高教学时间的利用效率，通常会设置多个教学班需要在同一时间开课这一要求[8]，称这样的一个教学班集合为一个同时上课组（第k同时上课组符号表示为：STimek）。一组同时上课的教学班所涉及的学生当中不存在任何学生的选课模式包含超过一个组内教学班。通常也不会有老师带超过一个以上的班级。一个教学班只可能属于一个同时上课组或不属于任何同时上课组。

从课时分配的角度来看，只有满足每天课时一致才有可能在日排课过程中构成课时对齐。这里将第k同时上课组在d这天的课时不一致表示为SameTime-Inconsistent(t,STimek,d)。计算中首先基于一周课时数对这个同时上课组成员进行从大到小排序，然后遍历所有成员，将该成员当天超出其他排在之前的成员的课时的数目相加。在获得每个同时上课组在每一天的同时上课违反值后累加获得同时上课整体违反情况，用如下公式表示：

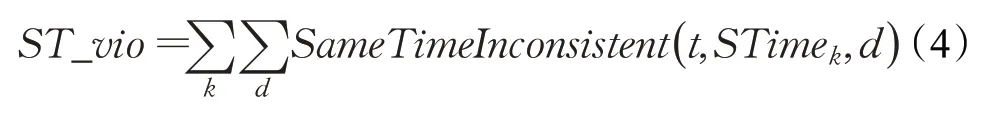
2.2.3 可排出不冲突课表的课时分配

课表在课时分配阶段不考虑是否不存在冲突，但必须考虑是否在下一阶段中不可能排出课时不冲突的课表，因此设计了“可排出不冲突课表的课时分配”约束条件。基于“课程班集合占用最少课时量”这一算法可以给出当前课时分配下一天所需时段数的一个下界，并结合该天的可用时段数给出约束违反程度。该约束条件可以涵盖单个或是多个学生老师一天课时过多，一周课时不够用等可能导致不可排课情况。根据这一约束条件可以提早做出课表调整避免无意义的后续优化。

这种不可排课现象可以表示为“最大全联通子图中的不可染色情形”。图论应用到排课问题中已有学者进行过一些研究，王凤和林杰[19]在高校排课问题研究中，将每个班级的每个课程抽象为图中待染色节点，颜色代表了上课时段，通过老师和学生的授课上课关系决定哪些课时不能在同一时间开设。这里用节点表示课程班，用无向边表示存在于同一个选课模式或由同一个老师代课。一个全连接子图是一个成员节点两两之间存在连接的节点集合，这个集合的存在意味着若这些课程班d这一天的课时相加后大于d(slots)，则这天不存在不冲突的课表。称这个图为课程班冲突关系图，GCClass_conflics。

课时分配过程可以继续细分为教学班课时分配和获得教学班课表后的行政班课时分配两种情形。在教学班课时分配过程中不仅需要考虑教学班范围内的课时过多导致的不可排课，还需要从每个行政班的角度考虑一周当中是否留有足够的行政班可用空间和每一天是否留有足够的行政班可用空间。

因为原理基本相同，这里仅给出教学班课时分配过程中“可排出不冲突课表的课时分配”的违反惩罚计算过程。在分配教学班课时之前需要确定各行政班的课时需求情况，这一过程独立于课表优化，可以仅根据课时设置推测得到。对于行政班x而言，将所有该行政班的课程班课时相加即可得到周最低课时需求，slotsWeekMin(x)；将课时数大于|Day|/2的课程班的课时数加和并除以|Day|后再将求得的商向下取整就可以得到行政班x的日最低课时需求slotsDayMin(x)。行政班的可用排课时段数大于周最低课时需求为可排必须满足的硬性条件，而日最低课时需求是出于对行政班课时均匀性的照顾，相对来说是一个软性约束。

“可以排出不冲突课表”的违反程度是以下三个部分的加和的结果：

公式中slotsDayExc是教学班课时超出量；slotsWeek-Uns(x)为行政班x的周最低课时不满足量；slots Day-Uns(x)为行政班x的日最低课时严重不足程度。这三组数据均由算法1直接或间接计算得到，这里表示为函数CCl ass_so_min(t,S_CCcurrent,d)。这个算法本质上是一个分支限界方法求解0/1规划问题。为了提升搜索效率，在算法中采用了堆结构存储分支，并在分支上界计算的过程中筛除与子图中任意节点存在不相连的节点。

算法1课程班集合占用最少课时量

输入：课表t，当前需要考察的课程班集合S_CCcurrent，天序号d，课时冲突关系矩阵ConflictMatrix。

输出：S_CCcurrent在d这天排出不冲突课表所需要的最小课时量。

该算法当中输入的课时冲突关系矩阵Conflict-Matrix是一个维度为|S_CC|×|S_CC|的对称bool方阵，这是一个不随课表变化的变量，因此在算法表示中没有列入输入参数。在生成该矩阵时，矩阵中的每一个元素初始化为0，如果存在一个学生的选课模式包含A、B两个课程班或一个老师被分配带这两个课程班，则将A课程班对应编号的行和B课程班对应编号的列所定位的元素值置为1。ConflictMatrix可以直接用作GCClass_conflics的邻接矩阵，在这个算法中判断两个课程班是否存在连接就是通过查询Conf lictMatrix得到的。堆activeHeap的每个分支将存储一个长度可变的向量和一个自然数，以这个自然数作为成员大小对比的依据。S[1]表示集合S_CCcurrent中第一个课程班的课时量，∑S[c1]表示集合中与第一个课程班存在直接连接的课程班的课时量之和，∑S表示集合中所有课程班的课时量。从步骤8开始使用的0/1向量C_visit与最大堆activeHeap所存储的分支向量结构相同，所有标记为1的节点构成的子集可以被视为一个全连接子图。C_visit的长度表示当前分支顺序访问到的节点，“位置在C_visit的长度之后”表示当前分支没有访问到的节点所处的位置，对于C_visit没有访问到的节点，如果与所有已经访问到节点中被标记为1的节点都有直接连接，则可以确保将这个新节点添加到子图中后依旧保持其全连接性，这些节点所对应的课程班才有可能被添加。每一个分支的上界为当前分支已经标记为1的课程班和没有访问到的课程班中可能被添加的课程班的课时总和。在这里选择使用的上界计算方法可以在降低上界的同时不会产生很高的计算消耗。如果在C_visit中没有包含任何1，则在计算上界的过程中需要将所有没有访问到的课程班的课时都加起来。

基于这个算法继续使用如下公式计算上文中提到的三个部分：

公式（6）将所有教学班的课程班纳入考察范围，e(k)表示一个阶跃函数，若实数k大于0则函数取值k否则函数取值0。有任何一天教学班无法排出不冲突课表都将带来惩罚。

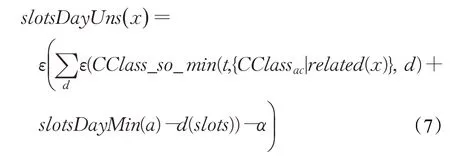
公式（7）中将与行政班x有关联的教学班的课程班纳入考察范围，{C Classac|related(x)}表示x行政班的学生选课模式所包含的教学班的所有课程班集合。α是一个预先设置的松弛变量，可以看作一周当中相关教学班占用课时累计超出量的容忍上限，过多的课时超出将带来惩罚。为提高兼容性，公式（7）的计算中允许出现一些天的少量课时超出。

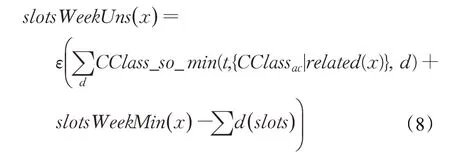
公式（8）中将每一天相关教学班最小占用课时的数量进行了累积，再加上行政班x的周最低课时需求后如果超出一周总时段数则将带来惩罚。

在这个约束的计算过程中，得到的产物不只是可以作用于课表评价的“可以排出不冲突课表”的违反程度值(Unable)，每个行政班每天是否得到了足够的空闲时段还将用于引导下面将要介绍的调整算子定向发挥作用，即计算slotsDayUns(x)的过程中相关教学班每天超出的课时占用量。用slotsDayOver(x,d)>0表示x行政班d天有课时不够。

2.2.4 教学班课时占用压缩

这是一个非必须的目标函数，需要结合排课任务来选择配置。在教学班同时上课规则覆盖大部分教学班时不需要添加此规则，但对于没有设置教学班同时上课规则或规则覆盖面较小的任务而言，教学班课表排课过程中的肆意分布可能导致在后期行政班排课过程中可用时段过少，这一状况对于开设重点科目的行政班而言并不理想。在某些整体课时安排非常紧凑的任务当中，可能出现教学班占用过多课时直接导致行政班无法排课这一状况，此时需要用这个目标函数来引导尽量压缩教学班占用的时段。教学班课时占用压缩目标函数和上面提到的周最低课时不满足量计算部分相似。但这里使用的不是阶跃函数而是分段函数，具体公式如下：

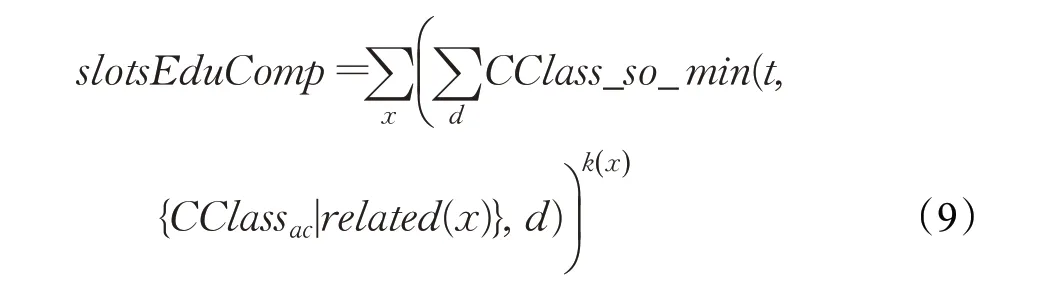
2.2.5 满足行政班可用排课时段

由于先于行政班排出的课表，排教学班课表的过程不受行政班课时的直接影响。教学班排课过程中课时不冲突这单一约束很容易满足，但不加限制的排课将减少接下来的行政班排课的可用时段甚至直接导致无法排课。得到教学班的完整课表后，从一个行政班的角度进行限制，其相关教学班占用时段都不能安排行政班课时，这可以从根本上保障学生上课不冲突。行政班获得的可用时段即可从所有时段中去除这些班级不排课时段得到。

承接上面的“可排出不冲突课表的课时分配”约束条件和“教学班课时占用压缩”目标函数设计了“行政班可用排课时段足够”这一约束条件和目标函数，来提升行政班排课质量。排除所有相关教学班有课的时段后即可得到每天和一周行政班可用时段数，从一天可用时段数的角度来评测是目标函数，从一周可用时段数的角度来评测是约束条件。每天的排课空间偶有不足可以接受，因此设置了最小化日时段不满足量，但一周可用时段数必须满足下限，即周时段不满足量必须为0。

2.2.6 课时优选

该目标函数在排课算法中广为使用[5，7]，评测方式可简单描述为不同科目有不同的时段选择偏好，如高考必考科目倾向于选择上午前几节这一时段，而体育等科目选择上午最后一节会有更好效果等。这一目标函数的细节在本文中不再赘述，仅给出如下测算公式：

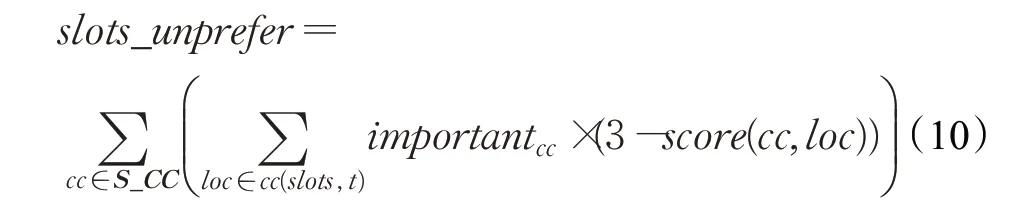
公式中cc(slots,t)为课表t中课程班cc所有课时所使用的时段，如果该课程班在课表中没有课时则为空集。score(cc,loc)为cc课程班在loc这个时段位置处的偏好得分，取值范围为{0，1，2}，分别表示不推荐使用、一般和推荐使用。为了和其他目标函数以最小化为目的相一致，这里取用3减去得分值作为时段选择不合适程度的度量。importantcc表示课程班cc的重要程度，通常与对应科目相关，也可细分到具体课程班。该目标函数将会遍历所有课程班的所有在课表中的课时。

3 课表（解）的表示与优化算子

在优化中仍然采用传统二维课表集的形式来记录中间解。这样可以保持每个课程班的课时数不会在优化操作中变化，同一班级多个课程班之间课时不重叠，并且一天的课时总数不会超过时段数。

在天课时分配阶段决策变量用CClassac(slots,t,d)即可表示。具体课时出现的时段是否为优选时段以及是否与其他班级的课表在这一时段处存在冲突都不会影响当前优化。这也意味着一张课表内同一天的两个时段互换内容不会引起目标函数变化。在课时分配阶段设计了如下三个算子：无评价均匀分布算子、同时上课修正和转移算子、不可排课情况下的教学班课时转移算子。

在天内课表优化阶段则必须要基于课表结构来表示。如前文所述这一阶段将不进行天之间的课时交换，因此部分优化操作、目标函数和约束违反的计算可以分天独立进行。此外还对课表初始化和课时交换做了修改以确保在课表变化过程中同时上课的满足程度不变。

3.1 无评价均匀分布算子

设计该算子的目的在于平衡每天课时，不需要对课表进行目标函数计算就可以直接得到尽可能满足课时理想分布的课表。由于在这一步当中不考虑由同一个老师授课或同一个学生上课引起的课表之间相互关联，每个班的课表调整可以独立进行。采用的基本策略是将课表中所有应当取出的课时全部取出后再依次放回到同科目课时最少并且有空闲时段的天。

以一个行政班的一个课程班为例，首先取出所有超过1课时的天当中除第一个课时之外的其他课时。若理想分布中不是每天都有课，则再以10%的概率取出一天当中所有剩余课时。所有课程班完成课时取出后重新置入刚才取出的所有课时。在放置每个课时之前，需要先统计出该班每天可以放置课程的空闲时段的数量availd。对于一个取出的课程班课时t，计算d天的课时放置压力Pd(t)，压力越大的天越不应该被选择，下面的计算公式中countd(t)代表d天课表中与t同科目的已有的课时数量。

这里的压力值可能为负数，为方便用轮盘赌方式选择放置到哪一天，采用归一化方法将压力值取负数并映射到0到1区间内，然后将每个映射值除以映射后所有值的和作为选择概率。从压力值的计算公式中可以看出，对于该天已存在课时的情况，会有较大的压力进而避免选择该天。如果每天都已经分布了相同课时则这些存在的课时不会影响选择。

该算子可能破坏原本已经满足课时理想分布的科目的课时分布，属于一种比较大范围的变化，因此不能频繁使用，否则将影响算法的收敛性。但作为一种解的初始化操作是一种不错的选择，因为其运用了均匀分布这一启发信息节省大量的目标函数值计算，同时又具有随机性。由于没有考虑到班与班之间的关联，而导致无法对老师教案平齐进行优化，因此还需要目标函数的引导和其他算子的精细调整才能实现教案平齐。

3.2 “同时上课修正算子”和“同时上课联动转移算子”

设计这两个算子用于提升和保障教学班的课时分配阶段中对同时上课规则的满足。在修正算子中依然使用集中取出后再有序放回的策略。在取出课时的过程中对于满足同时上课一致性的教学班集合不取出课时，而对于超出上限的成员教学班取出课时至其上限。虽然这将引起当天课时变化，但可以观察到对任意成员而言当前课表所确定的课时上限是不会改变的，因此课时取出时的顺序对结果没有影响。放回过程则不然，必须从课时最多的成员到课时最少的成员逐个放回。在满足放置一个课时后不超过课时上限且有空闲时段的天当中随机挑选一天放置课时。如果无法找到这样的位置则随机挑选一个空闲时段放置。该修正算子将依次作用于每一条同时上课规则。

同时上课联动转移算子的作用范围要相对较小，需要事先选定调整哪一组同时上课然后通过课时转移实现对调两天的课时数这一目的。该算子发挥作用需要同时上课规则内满足下列两个条件中至少一条：（1）成员之间理想课时分布不一致；（2）理想课时分布中存在若干天不上课。根据规则中每个教学班在选定的两天的课时差D，检查课时相对较少的一天内是否有足够的空闲时段。如果有则将最先遇到的D课时转移到课时较少的一天中，否则不进行转移。联动转移算子的设计初衷是在不改变任何科目的分布理想程度情况下，通过改换多课时或无课时的天来改变同时上课的整体分布，使得教学班的课时分布更为平均以及从行政班角度来观察时占用课时更少，这一情况对应于多个同时上课组之间允许（或必须）存在课时重叠。

3.3 不可排课情况下的教学班课时转移算子

结合约束条件计算的结果slotsDayOver(x,d)，对行政班某天的缺少可用空闲时段这一情况，该算子将套用同时上课联动转移来针对性解决。算子输入某一天D存在行政班缺少可用空闲时段，然后遍历每一条同时上课规则，如果有其他天C比D这一天占用的课时数要少，则交换这一条同时上课规则C，D两天的课时实现减少D天安排的课时数，这里推荐选择占用的课时最少的一天作为C。鉴于一个行政班的相关教学班可能存在于多个同时上课组内，不继续细化针对单个行政班或同时上课规则进行处理，而是交给目标函数来引导优化。D这天当中上课的教学班如果没有被同时上课规则覆盖到，则需要采用与上文中“无评价均匀分布算子”类似的方法来变换课表。集中从这一天中取出所有课时后，再放到其他天的空闲时段当中，如果该课程班的课时理想分布需要每天都有课时则为该天保留所需的最小课时，通常为1课时。

3.4 天内课表优化阶段课表初始化和课时交换操作

天内课表优化阶段不是本文的核心讨论过程，本文也没有做出主要贡献，因此只对以下几点与文献[6]中使用的课表变换（生成邻域）算子的差别进行说明。这一阶段课时交换只发生在一天之内的两个课时之间，邻域选择必须限制在一天范围内的若干时段中。在教学班课表确定后，行政班课表当中将对有任何相关教学班上课的时段赋予特殊标记，这些位置不可置入任何课时，同时也不能参与到任何课时交换操作中。也就是说将成为“不再被视为空闲”的时段。

教学班的同时上课将由课表初始化和联动交换策略保障。具体来说就是在初始化课表的过程中就参考同时上课规则，逐课时将组内成员同步放置在相同时段，如果分配课时不同则对放置部分课时后仍有剩余的成员继续同步放置操作。在课时交换中采用的联动交换策略要求对选定的两个时段内同时上课规则涉及到的若干课表同时进行交换，进而从根本上保障任何课时交换操作都不会引起同时上课的满足程度发生变化，于是也就没有必要对此设计目标函数进行同时上课满足程度测算了。

4 算法流程

4.1 目标函数和约束条件选择

基于天课时分配的多阶段新高考“走班”排课算法是4个阶段顺序进行的。每一阶段都是一个优化过程，输入的初始课表为前一阶段优化得到的课表。最后一阶段的输出课表是最终的算法输出课表。

第一阶段优化教学班课表课时分配，操作的决策变量为全体教学班课表，此时行政班课表为空，评价行政班课表的目标函数值和约束违反值全部记为0。目标函数和约束条件分别为：

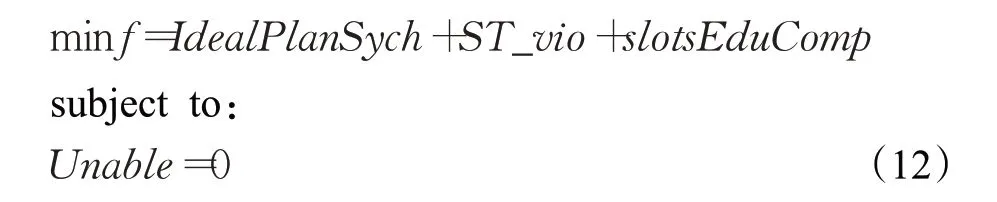
这一阶段考虑因素包含教学班课表每天的课时分布质量，同时上课规则满足，行政班可用空间最大化，以及不出现已知潜在不可排课因素。由于行政班课表尚未确定，这一阶段只能通过目标函数来为未来行政班排课创造尽量宽松的空间。

第二阶段优化获得教学班完整课表，操作的决策变量为全体教学班课表，采用文献[6]中已有的模拟退火算法，同时改用上文提到的课表变换算子。目标函数和约束条件分别为：

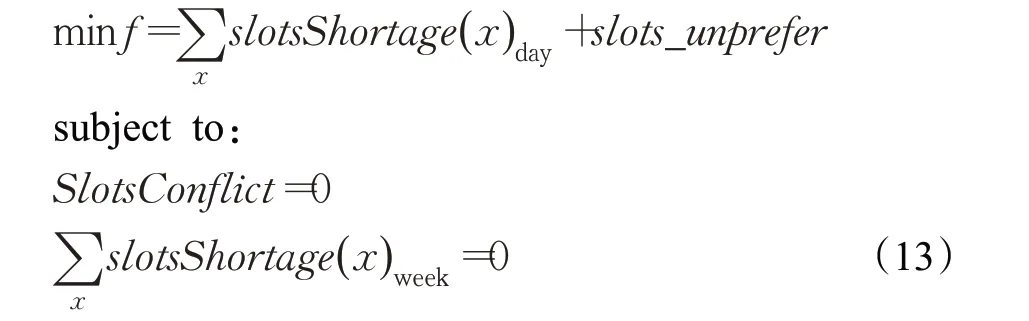
该阶段课表优化的核心考虑因素是：（1）通过约束条件确保教学班之间不出现学生和老师课时冲突；（2）通过约束条件确保行政班一周排课空间足够；（3）通过目标函数降低行政班排课难度，这其中要求每一天的教学班的课表可以为相关行政班保留足够的可排课时段；（4）通过目标函数进一步优化课程的时段选择的合理性。这样设置的依据在于该阶段将完全确定教学班课表，行政班可用时段也将确定。这一阶段输出满足约束条件的课表则说明可以继续接下来的排课。

第三阶段优化行政班课表课时分配，操作的决策变量为全体行政班课表，教学班课表存在且不能改变。算法流程和优化教学班课表课时分配相近，目标函数和约束条件分别为：

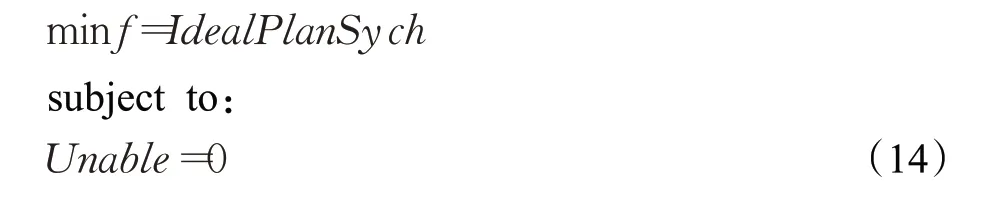
由于规则当中没有涉及行政班的同时上课规则，这里与第一阶段有不同。行政班课表排布过程可以充分利用可排课时段，因此不需要也不存在占用课时压缩。这一阶段仅保留了对行政班课时分布的优化这一核心目标，核心难点在于因为教学班课表已经存在导致可用时段不如第一阶段丰富。

最终阶段优化获得行政班完整课表，操作的决策变量为全体行政班课表，同优化获得教学班完整课表步骤相同。目标函数和约束条件分别为：

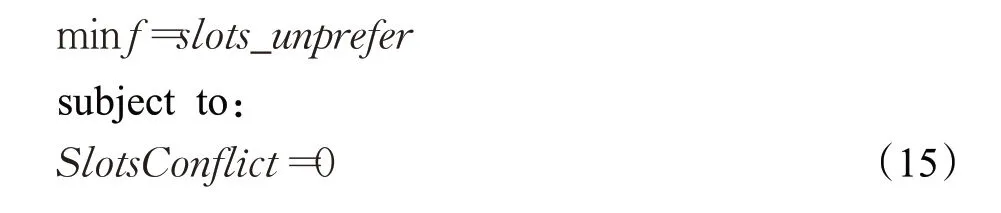
这一阶段中课表已经基本定型，仅需要天内课表微调操作，因此所需要考虑的核心是不出现冲突。课时优选依旧为深度优化所需要考虑的目标。

可以将第一、三阶段视为第二、四阶段的前置优化过程，所考虑的因素都为通过课时分布即可评价质量或估计输出课表对规则满足程度以及课表可排性的目标函数和约束条件。这里将规则满足的高压力和复杂的跨天调整以及更大的课表调整自由度相结合，集中精力攻克走班排课除课时冲突外的难点。

4.2 一种适用于优化教学班课表课时分配的爬山算法

第一阶段优化教学班课表课时分配是整个算法的核心部分，为此提出了一种改进的爬山算法来解决这一约束优化问题。该算法借鉴了孟凡超等[20]用混合遗传模拟退火算法解决软件优化配置问题的经验，融合了VNS机制提升爬山算法的搜索更优解的能力。

启发式算法看重的两个重要能力在于向局部最优收敛的能力和跳出局部最优能力[21-22]，并不要求搜索最终停留在全局最优处，而是通过记录算法中找到的最优解实现全局收敛。相较于简单的爬山算法，VNS允许在相对较差解的附近进行有限代价的搜索以期望找到另一个局部最优的解，因此添加VNS机制弥补了爬山算法易于陷入局部最优的缺陷。在优化算法运行初期，随机产生的初始解很大概率处于一个目标函数较劣的局部最优附近，因此借助VNS机制跳出该区域，使得当前最优解向更优的区域内收敛。在向局部最优收敛的过程中，采取的策略是遇到目标函数更优的解或过于差的解时就终止VNS，并以当前最优解为起点重新开始VNS，这种设计提升了收敛速度。在算法后期，已经接近或达到较大范围内最优解的情况下，VNS机制将主要保留向更远区域探索的能力，从而提升输出结果收敛到全局最优的概率。

算法2给出了这个算法的伪代码描述。

算法2优化教学班课表课时分配的爬山算法

输入：各教学班的各科目的课时安排；老师带班情况以及教案分组；教学班同时上课规则；各行政班学生的选课模式；各行政班各科目的课时安排；总迭代次数total_iteration。

输出：教学班课表。

在步骤1中放置教学班的课时在课表中的任意位置，保障课表是一个课时完整的初始解。步骤2通过执行一次无评价均匀分布算子和同时上课修正算子提升了初始解的质量。步骤4使用两个课表变量保留优化过程中间产生的历史最优解和临时最优解，历史最优解保障了算法的全局收敛性，这一做法借鉴了遗传算法当中广为使用的精英保留策略；而临时最优解提供了一定的局部搜索能力和探索解空间中其他区域的机会。步骤5设定了部分控制算法运行的参数，包括主循环次数和局部搜索尝试次数。

步骤8起到一个策略选择器的作用，这里采用随机策略选择的方式，因策略之间存在的差异，三种策略的选择概率比为1∶2∶7。策略1使用的变换是对原有解较大范围的变动，因此过多的使用将导致收敛速度变慢；策略2利用了约束条件计算中获得的启发信息，针对解决可能存在的约束条件不满足并可以就这一情况的具体位置进行解的变化。在初期寻找满足约束条件的解过程中发挥核心作用，若当前解已经满足约束条件，策略2等同于策略1。策略3是一种解的微调操作。对于有同时上课规则指导的排课任务而言，多课表的联动调整将有利于避免打乱原本的同时上课课时分配一致性。对于没有同时上课规则的排课任务而言，该策略重点通过单教学班的随机跨天课时调整来压缩教学班课时的占用，这一步有可能带来目标函数中其他指标的恶化，所以只能重复执行很少次。

步骤28仅仅测算当前解的约束违反程度，在当前解不满足约束条件的情况下不测算其目标函数值，以减少不必要的计算消耗。步骤30保留了寻找满足约束条件的解的能力，以应对满足约束条件的解比较难以寻找的排课任务。步骤33至35和步骤46至48的设计初衷是在当前解的目标函数值与历史最优解的目标函数值差距不太大的情况下保留其通过上述变化算子继续探索的机会。临时最优解在此充当局部寻优搜索起点，指导当前解向更优解变化，若多次尝试均未超越历史最优，则从历史最优解重新出发重新探索，这期间如有产生不满足约束条件的解也可以回到临时最优解重新搜索。整个算法在寻找第一个满足约束条件解的过程中采用贪心的策略，并在获得满足约束条件的解之后采用对违反约束条件零容忍的态度进行优化，以期达到快速稳定的找到满足约束条件解的目的。针对满足约束条件的解，在寻优过程中采用适当宽松的策略允许在非最优解附近进行局部搜索。

5 数值实验

5.1 实验数据与性能评测方式

本文选取了一个人工生成的排课案例和两个改编自真实学校的排课案例来测试该算法的性能。评测采取若干次独立运行后统计输出课表的各项指标的均值和方差来体现课表质量以及稳定性，这些指标包括教案平齐、课时分布均匀、教学班同时上课、行政班天可用时段以及课时优选。优化算法的计算用时也一并给出。稳定性除了目标函数值的方差外，成功排出满足约束条件的课表次数占总实验次数的比例（成功率）也将同步给出。

人工生成的案例包含4个行政班和10个教学班。课表中总共出现11门科目、30个选课模式、18位老师，该数据不包含同时上课规则。一周上课时段为6天，每天9课时。

两个真实案例为对某高中的排课案例进行适当修改后得到的。其中中等规模案例包括8个行政班和15个教学班。课表中总共出现11门科目、359位学生（共20个选课模式）、28位老师、三条同时上课规则。一周上课时段为5天，每天8课时。大规模案例包括20个行政班，45个教学班。课表中总共出现14门科目、854位学生（共95个选课模式）、70位老师、7条同时上课规则。一周上课时段为6天，每天9课时。

评价课表质量将在完整获得课表后进行，也就是对一个真实课表进行评判。指标采用上文中给出的计算公式进行度量。若通过计算发现，优化得到的教学班课表无法再排出不存在学生冲突的行政班课表，或教学班本身存在学生或老师课时冲突，则终止后续优化并记为排出课表不满足约束条件，同时将不再排行政班课程。行政班课表中存在课时冲突同样也将被视为排出课表不满足约束条件。所有呈现在图表中的目标函数值和计算用时的测算均基于满足约束条件的课表来测算。

5.2 优化算法相关参数设定与实验平台配置

在教学班课时分配阶段：总迭代次数为500，满足课时均匀的教案平齐中的权重w1=5/6，行政班的日最低课时严重不足程度α等于；在行政班课时分配阶段：总迭代次数为100，其余参数与教学班课时分配阶段一致；在天内课表优化阶段中使用的模拟退火算法[6]初始温度为2.5，停止温度为1，降温速度参数为0.99，较差解接受控制参数为0.5，相同温度下内循环次数为200。

仿真实验使用C++实现，集成开发环境为Visualstudio 2019。算法运行计算机配备如下：操作系统，Windows 10专业版64位；处理器，英特尔Core i7-7700 3.60 GHz四核；内存，16 GB DDR4 2 400 MHz。全部实验采用单线程进行。

5.3 实验结果分析

表1中给出了本文提出的算法在三组数据集上的运行结果数值统计。该表格中的每一组实验数据中成功率是基于200次独立重复实验得到的，其他指标统计是基于这200次实验中成功排出的所有课表中随机选取100张课表得到的。针对每个数据集表格中依次给出平均优化运行时间、教案平齐不满足程度、课时分布均匀性不满足程度、教学班同时上课不满足程度、行政班每天可用的排课时段的紧缺程度、课时优选不满足程度的平均值、最优值、方差，这些指标都是越小越好的。人工生成案例中没有设计同时上课规则因此这一项为空。为研究同时上课规则的有无对课表优化的影响，也在删去同时上课规则后的真实案例上进行了实验，结果也包含在表1中。

从表1中可以看出，本文设计的优化算法可以以较高的成功率求得满足约束条件的课表，大规模问题平均运行时间在10 min左右，属于可以接受的范围。有无同时上课规则对各项指标均有影响，其中中等规模真实案例中教案平齐、课时分布均匀受影响较大，无同时上课规则的案例相关指标有明显提升。大规模真实案例中成功率、运行时间、行政班天可用时段也表现出受影响明显。同时上课规则的有无还对部分目标数次运行所能达到的极值存在影响，例如中规模真实案例中的教案平齐和两个真实案例下的行政班天可用时段。

表1 运行结果数值统计

通过大量重复实验和改变目标函数权重以及人工微调课表方式，对这三组案例在教案平齐和课时均匀分布这两个目标上的极限最优值进行了探索。人工生成案例在教案平齐违反上可以降低到0；大规模案例中教案平齐违反可以降低到82，课时分布不均匀可以降低到0。由此可见该算法在人工生成案例上寻找不违反教案平齐的课表的能力有待提升，在其他指标方面随机多次运行可以十分接近指标的极值。课时优选这一目标的优化不是本文的重点，因此没有对这个评价指标进行分析。本文推测，大规模案例实验中若干评测指标未能降低到0主要是因为问题规模过大，需要消耗更多的计算代价，同时规则设置可能存在不合理之处，使得规则之间存在矛盾关系导致课表整体质量不佳。

继续对实验中产生的课表进行分析，拆分出教学班和行政班测算在分课表上的教案平齐不满足程度。在大规模真实案例和人工生成案例这两组数据的实验中生成的课表这一指标表现不够理想，因此对这些课表进行了观测，大规模真实案例采用的课表来自有同时上课规则的案例。首先以完整课表的教案平齐不满足程度对产生的所有课表进行排序，然后依次取10%的课表对其教学班的教案平齐不满足程度以及行政班的教案平齐不满足程度求平均值，其结果如图2（a）所示。从图中可以看出对教案平齐违反程度贡献最大的是行政班的教案平齐违反，而且其增长直接带来整体课表的教案平齐违反程度提升。教学班的教案平齐违反较少，且变化不明显。使用本文提出的算法可以获得较为理想的教学班课表，但行政班课表质量还有待提升。

同时还分别以行政班课表和教学班课表的教案平齐不满足程度排序课表后画出相似折线图，图2（b）和图2（c）。图示结果表明教学班课表的教案平齐违反程度对整体课表教案平齐不满足贡献有限。图3是对人工生成案例下生成的课表观测的结果，相关结论与大规模真实案例一致。

图2 教案平齐满足与位次分组的关系（大规模）

图3 教案平齐满足与位次分组的关系（人工生成）

前面实验初步表明同时上课规则的有无对中等规模真实案例的课表优化结果有影响。为进一步观察教学班同时上课规则部分缺失情况下课表优化结果的差别，选择受影响最为明显的中规模真实案例进行下面的实验。首先随机删除部分教学班同时上课规则生成12组新的同时上课规则。具体做法是从原有同时上课规则中分别整班随机删除20%、40%和60%的教学班，每一次随机产生4套不同的规则形成独立测试案例，这样获得了除同时上课规则不同外其余数据和规则完全相同的12组测试数据。没有选择从规则中删除80%的教学班，原因在于将出现多条规则只包含一个教学班这种无效同时上课规则的情形，这一情况下排课任务无异于没有同时上课规则。每一组数据下进行30次独立重复实验，得到课表在教案平齐、课时分布均匀、行政班天可用时段、课时优选这四个目标上的表现如表2～4所示。在这一实验当中教案平齐、课时分布均匀、行政班天可用时段基本符合指标随同时上课涵盖教学班的数目减少而变差的预期。不同随机案例表现出不同的平均结果，说明相同涵盖范围的同时上课规则本身还存在对课表优化引导的差别。观察不同同时上课规则对应的最优结果，发现规则差别对其影响较小，并且这一现象在大规模真实案例有无同时上课规则的两组实验结果中也可以观察到。

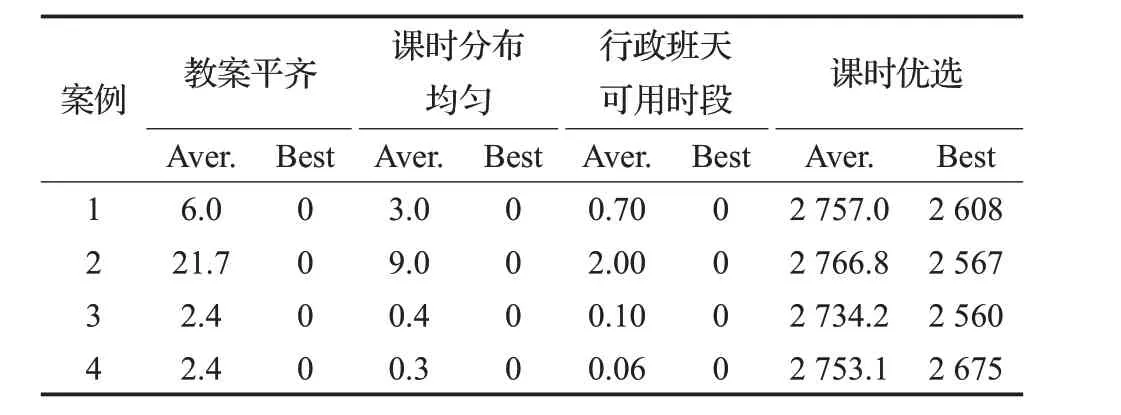
表2 删除20%同时上课规则后课表质量的统计结果

表3 删除40%同时上课规则后课表质量的统计结果

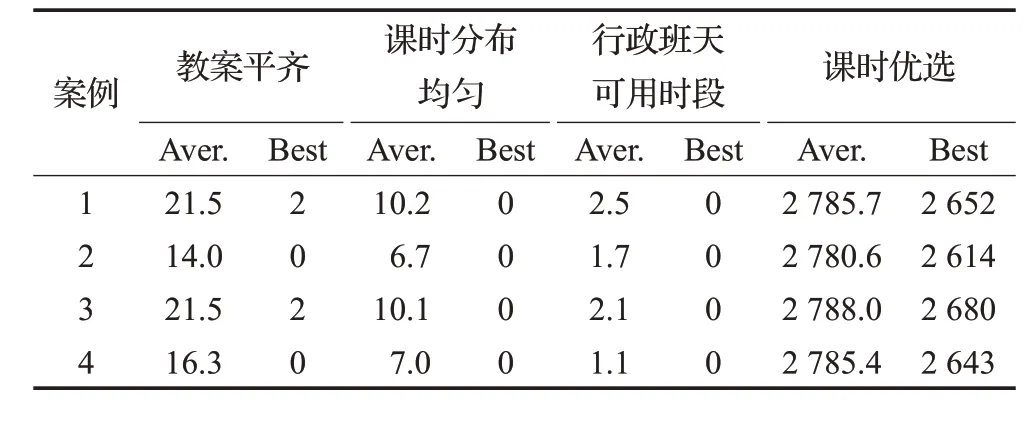
表4 删除60%同时上课规则后课表质量的统计结果

6 结束语

本文针对“新高改”政策下的高中走班制教学排课问题进行了研究，设计了一套基于天课时分配的多阶段课表优化算法。从每天课时分配的角度对课时分布均匀程度、授课老师教案平齐满足、分配课时可以排出不冲突课表等目标函数和约束条件进行了数学建模。还在三组测试数据上验证了所提出算法的性能。实验结果表明该算法在可以接受的时间内以较大概率得到课时不冲突课表。除大规模真实案例对教案平齐满足程度优化不理想外，其他参数指标均可得到较理想的优化。进一步观测发现，教案平齐违反主要来自于行政班课表，同时上课规则的有无和对教学班的覆盖完整程度影响到对其他目标的优化。因此建议在排课之前充分准备教学班的同时上课规则。

排课是一个复杂并且需求多样的优化问题，需要根据排课任务所包含的数据规模以及难点配置算法参数和选用算子。未来还将进一步改进算法适配问题的能力，并探索走班排课问题复杂程度的分析方法。期望能在排课之前估计最终课表质量的上限和指出规则设置的不合理之处，供用户调整排课方案。