改进核密度估计的空间点密度算法
饶加旺,马荣华
1.江苏省测绘工程院 空间信息技术研究中心,南京210013 2.中国科学院 南京地理与湖泊研究所,南京210008
点密度是一定范围内点数量的统计值,是地理空间分析的重要任务[1-2],而核密度分析是点密度分析常用的重要方法,它是根据核密度估计函数(Kernel Density Estimator)将平面的二维离散点生成连续的三维表面,计算事件点在设定的周围邻近空间的密度的过程,直观地反映点群的聚集或离散分布特征[1]。相比较于其他空间分析方法,核密度分析需要参数较少,受主观因素影响较小,因而成为了地理空间分析中应用最广泛的方法之一[2],被广泛应用至地物空间分布[3-4]、空间区域格局分析[5]、疫情监测与分析[6]、地质灾害与自然资源环境监测[7-8]、路径优化与分析[9]等诸多领域,从空间上获取事件的宏观分布特征。研究者相继开发出适应R、Python、ArcGIS等多种编程语言和软件环境下的算法。Kern-Smooth是R语言环境下用于计算核密度的功能包,按照核函数的不同可分为bkde、bkde2D、bkfe等函数,其中kde2d是R语言环境下应用最为广泛的密度函数[10-11],该函数主要使用高斯核密度估计实现函数的平滑,以三维连续表面的形式输出点的概率密度[12]。KernelDensity为Python语言环境下计算核密度常用的功能包,实现方式、功能与R语言中的KernSmooth类似;ArcGIS软件在Spatial Analysis工具箱中集成了核密度分析功能,用于衡量单位面积内点要素的量值[13],在可视化输出方面常借助核密度函数(或平滑函数),将离散点在空间上拟合为连续的光滑锥形表面,再以不同的颜色分级表示密集程度[14]。
相关研究发现,核密度分析对于描述连续现象的应用场景效果较好[1],而对于离散点,虽能表示空间格局、事件的分布特征及趋势变化,但密度空间分布模式上存在的“距离衰减效应”[15],在利用ArcGIS软件或kde2d等算法实现核密度分析时常存在如下问题:(1)分析的结果通常会把本身并不活跃的区域纳入计算范围,不仅改变了点原有的空间位置,也改变点的离散性质,存在过度拟合的情况;(2)运算时需预先设置计算空间范围[10,13],常导致额外的资源开销,当数据量较大时,运算耗时较长、效率较低;(3)可视化输出时,不同的颜色分级表示的密度分布难以反映离散点真实的密度情况;(4)主观影响较强,设置带宽、搜索半径与输出单元格等参数通常依靠经验,较大的搜索半径与输出单元格常导致难以准确地反映事件分布情况,整体空间形状变形较大,而较小的搜索半径与输出单元格又会对核密度分析带来巨大的计算量与计算资源的消耗。在不改变离散点位置的基础上获取点的真实密度值在疫情监测[16]、军事领域、灾害监测与统计[17-18]、地图制图[19]、社会治安与应急管理[20]等领域中具有重要应用。为此本文在核密度分析的基础上提出了空间点密度算法,利用几何投影与哈希数据结构,在不改变离散点空间位置以及离散特性的基础上,降低主观性对结果的影响,快速度量点真实数量的方法,以提高点密度的真实分布与高效的可视化输出。
1 核密度算法
对于非均匀分布的离散点而言,假设用λ(u)表示空间位置u的密度,将任意空间范围B划分为无限多个子区域ai,范围B内点密度可表示为λ(u)ai,因此B范围内点密度E[B]可表示为所有子区域点密度之和,则:
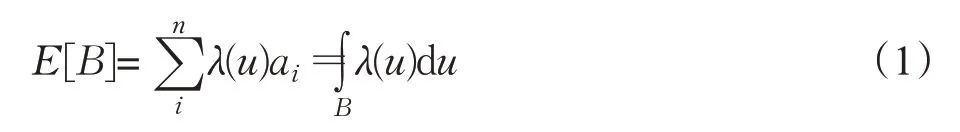
式中,n为点的个数,λ(u)可通过核密度算法进行无参化计算得到[1]。
1.1 划分格网
将研究区域划分为多个单元格网,定义搜索窗口W,逐一遍历单元格网,对于特定位置v,当其在W内时f(u)=κ(v-u)(f为空间位置u的函数,κ为核函数),反之,则f(u)=0。
1.2 获取密度贡献值
获取W内各个格网对整体的密度贡献值,其值为W内所有点xi数量之和,用坎贝尔方程来表示[1]:
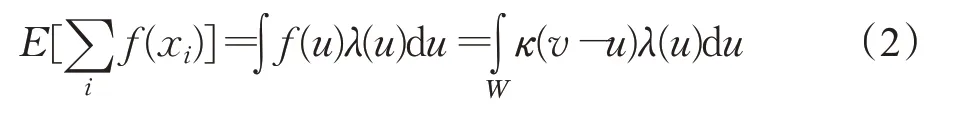
1.3 输出核密度
计算并输出每个单元格网的密度值,该值为W内所有点对格网密度贡献值的和,根据公式(2),则:
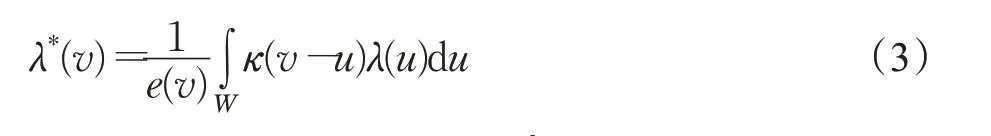
e为边缘校正参数,可表示为λ(v)经过核密度函数平滑后的估计值,可视化输出的效果是将二维的离散点变成三维连续的光滑平面,通常具有偏差,因为前者消除了点位的离散特征、真实位置等具体信息[1]。
2 空间点密度算法
本文提出的空间点密度算法是在保持点的离散属性与初始空间位置的基础上,统计并计算每个搜索邻域内点的单位真实数量,快速输出离散点的位置与点密度值。假设圆心O代表了网格点最近的一个事件,研究区域内有n个点,其纬度、经度分别由lati、loni表示,g代表格网的大小,r表示用于搜索的邻域半径,tlati和tloni为最邻近格网点的纬度和经度;为了使构建点密度算法具有可解析性以及保证算法运行的高效性,定义两个哈希表bin_density_hash()与density_hash(),其key值分别为邻近格网点与邻域内格网点的经纬度坐标值。
算法分为离散点的分箱与降维操作、计算格网内点的密度、维度的再膨胀三个步骤。算法的流程图如图1所示。
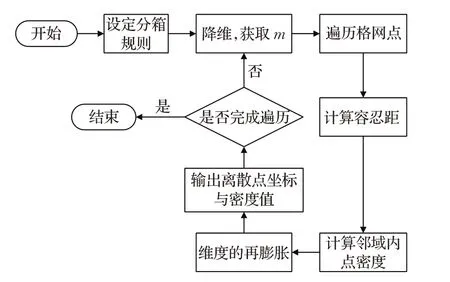
图1 算法流程图
2.1 离散点的分箱与降维
执行时初始化参数r与g,将研究区域划分为等距的格网,使邻域中心点与格网相叠加,对邻域内的离散点执行分箱操作,分箱的规则是通过近似的方式获取每个点在其最近格网点的坐标。当执行完成时,数据的维度由n降至m,bin_density_hash()的地址值为装箱操作后点的数量值,该值为改变点的位置所得到的,为相对值,作为后续运算重要的数据基础,伪代码如下:

2.2 计算格网点内的密度
该步骤是本文算法的核心,示意图如图2所示。首先遍历m个格网点,获取邻域内格网点F的坐标(lat1,lon1);其次沿着中央经线方向自下而上迭代运行,依次从F点遍历至G点,通过上下移动的距离l,以及邻域半径r计算容忍距t;然后以g为步长遍历经度方向的点E1至E4,并将其经纬度坐标存储至density_hash()表中,统计被记录次数,依此类推直至遍历至点G完成邻域内所有格网点的循环。容忍距t是识别邻域内点经度的重要依据,确保了只有在邻域范围内的密度值是增加,避免了算法额外的循环,是本文算法高效运行的关键。当遍历结束后,density_hash(latt,lont)的key值为经过分箱操作后点的经纬度坐标值,地址值为离散点真实的密度值,此时数据的维度仍为m。
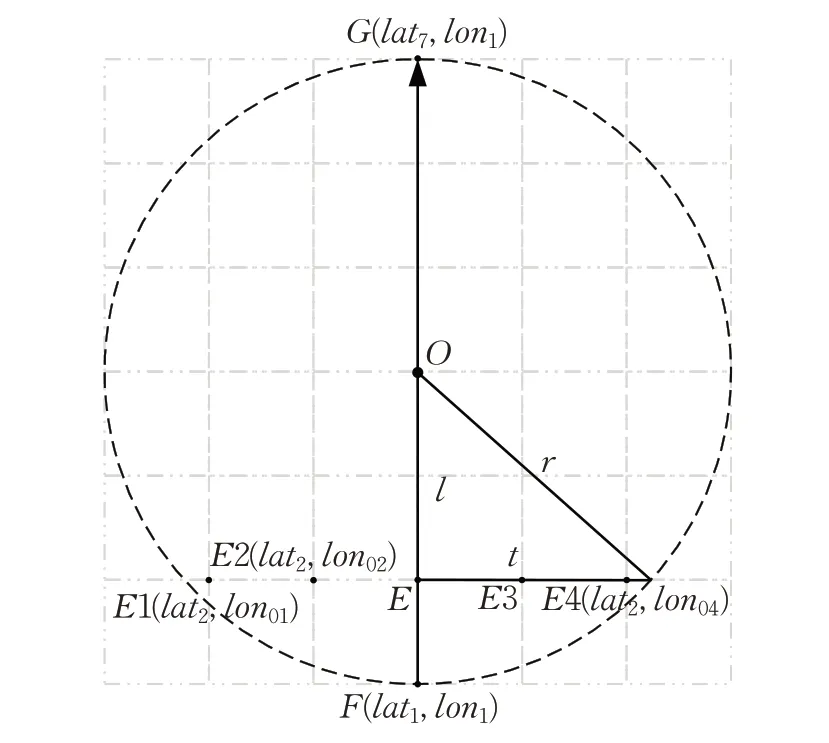
图2 计算格网内点的密度示意图
伪代码如下:


2.3 维度的再膨胀
遍历n个点,依次从density_hash(latt,lont)的地址值中读取点的密度值;将离散点初始的经纬度坐标与实际的点密度值相关联,若未完成遍历,重新执行步骤2.1~2.2,直至完成整个研究区域的遍历,最终输出结果为n个离散点的初始坐标与对应的密度值。伪代码如下:

3 实证研究
美国地质调查局(United States Geological Survey,USGS)的国家空间数据基础设施节点(National Spatial Data Infrastructure Node)提供了美国50个州的水资源数据信息[21],共计约190多万条,包括地表水、地下水等类型的站点编号、站点名称、经纬度坐标等字段,该数据作为开放的数据集,具有数据格式化程度高、区域跨度和数据量均较大等特点。本文基于R语言编写网络爬虫程序,抓取了截止至2014年12月31日的美国大陆(不包括阿拉斯加、夏威夷、关岛等地区)所有的地下水资源的数据信息,共由1 233 186个离散点组成的数据集,作为本文算法的验证数据,如图3所示。
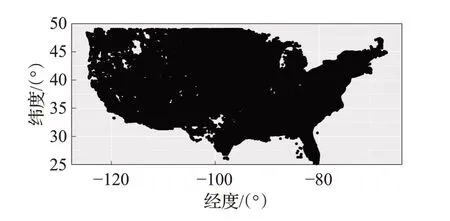
图3 验证数据的情况
3.1 可视化运算实验结果
在R语言环境下,读取美国大陆地下水资源数据集。兼顾可视化效果与运算次数,将格网大小g与邻域半径r分别设置为1、5,借助ggplot2功能包[22],将点密度执行的结果可视化,返回结果包括离散点的初始坐标、密度值,如图4所示。

图4 空间点密度可视化结果
3.2 与核密度算法的比较
3.2.1 可视化效果
在ArcGIS 10.4.1软件环境下,执行Kernel Density操作,分别将搜索半径与输出单元格的大小设置为0.1、10,得出如图5(a)所示的结果。由图可知,可视化输出的结果为连续的,图4中空白区域也被拟合成连续的区域,整体形状发生了改变,图中点的位置发生了变化,存在过度拟合的情况,当搜索半径与输出单元格的值均较大时,整体的形状改变越剧烈;而过于密集的网格对核密度分析带来巨大的计算量和计算机软硬件资源的消耗,此外,由于整体形状发生了改变,此时的密度值为空间加权平均值,导致密度值的真实性与可识别性均较低;在R语言环境中执行kde2d算法[14],分别设置带宽与输出单元个数为0.1、3 000,输出的核密度结果为碎片化的面状形式如图5(b)所示,存在离散点位置发生变化而被过度拟合的情况,密度的可识别性较差,同时存在点缺失的问题。当设置较大的带宽与输出单元时,存在更多区域被过度拟合的情况。本文算法最大程度降低了主观性对于结果的影响,通过设置不同的格网与邻域半径,如图4与图5(c)(格网大小与邻域半径分别设置为10、100)所示,改变的仅是点的相对密度值,而不会改变离散点整体的形状,输出的结果仍为设置的格网与邻域半径下真实的点密度值。因此本文算法的可视化效果与点密度的可识别性均优于ArcGIS 10.4.1软件与kde2d算法。

图5 与ArcGIS核密度、kde2d的可视化效果比较
3.2.2 算法效率
评价算法的效率,通常通过统计算法中基本操作重复执行的次数(时间复杂度)来衡量,使用O(n)表示[23]。kde2d算法的时间复杂度为O(nm)[11],本文算法的时间复杂度为O(n(2r/g)2)。为验证不同样本数量下两种算法的时间复杂度对比情况,依次从数据集中随机取5 000、10 000、50 000、100 000、500 000、1 000 000个点共六组样本,样本分布如图6(a)~(f)所示,依次通过本文点密度算法,得到的结果如图7(a)~(f)所示,两种算法的时间复杂度的比值情况如表1所示。
本文算法与kde2d算法的时间复杂度均与样本数量n有关,前者还与设置的格网大小g与邻域半径r相关,后者与离散点分箱操作后格网点的数量m相关。将两者的样本数量设置为相同,如表1所示,当数据量从小到大时,由于m≫(2r/g)2本文的空间点密度算法的时间复杂度均低于kde2d算法;当数据量逐渐增大时,本文的算法效率优势较明显,表明本文算法更适合大数据环境下计算离散点的密度值。因Environmental Systems Research Institute(ESRI)官方尚未公布ArcGIS软件Kernel Density算法的源码[13],因此以运行时间为指标将本文空间点密度算法与ArcGIS软件Kernel Density算法进行对比,计算机运行环境为CPU:Intel I7-6700HQ 2.60 GHz,内存:16 GB,操作系统:Windows 7专业版64位,软件系统:R 3.5.0、ArcGIS 10.4.1版本,执行时将Kernel Density搜索半径与输出单元格设置为1、5,将本文算法的格网大小与邻域半径设置为1、5,两种算法各执行20次,取平均所耗费的时间如表2所示。
总体而言本文算法的运行时间比ArcGIS的Kernel Density较长,尤其是当数据量较大时。究其原因,首先ArcGIS软件的Kernel Density函数封装与模块化应用较好,可较大程度地利用计算机资源,程序读写与运算的效率较高;其次在算法机理上,Kernel Density是对二维离散点表面进行内插,计算格网对整个区域密度的贡献值[13],因此遍历的次数相对较少,而本文算法为保持离散点的初始位置与获取真实的点密度,在执行分箱操作、计算格网内点的密度、维度的再膨胀过程时遍历次数较多,导致耗时较长。

图7 不同样本数量下的空间点密度计算结果

表1 不同样本数量下算法效率对比情况

表2 算法运行时间对比情况s
4 总结与展望
针对目前核密度分析计算点密度存在着改变离散点位置与属性、密度值可识别性较低、运算效率较低以及主观因素对输出结果影响较大等局限,提出了空间点密度算法,该算法在保持点的离散属性与初始空间位置的基础上,通过设定分箱规则,获取离散点最近的格网点坐标;依次遍历、统计并计算搜索邻域内点的数量,最终输出离散点初始坐标与点密度值,算法共分为离散点的分箱与降维、计算格网内点密度、维度的再膨胀三个步骤。
引入USGS网站发布的美国大陆123多万条地下水资源信息作为验证数据,通过验证与分析,该算法最大程度地降低了主观因素对于计算结果的影响,不改变离散点的属性与整体形状,在可视化效果与点密度识别性上均优于ArcGIS 10.4.1版本的核密度法与kde2d算法,运算效率优于常用的kde2d算法。由此可视化效果与算法时间复杂度验证均证明了本文空间点密度算法的有效性。但实验结果同时表明,当数据量为百万级别以上时,将格网点与邻域设置较小时,存在消耗计算机较大内存、运算时间较长的情况。为此,后期工作重点将进一步优化算法,减小内存消耗、缩短运算时间。

