深度稀疏自编码器在ECG特征提取中的应用

郑淋文，周金治，黄 静

1.西南科技大学 信息工程学院，四川 绵阳621000 2.特殊环境机器人技术四川省重点实验室，四川 绵阳621000

心电信号的智能化分析技术是智慧医疗和远程医疗的研究热点[1]。ECG分析通常包括信号采集、信号预处理、特征提取、自动分类。其中特征提取和降维是保障ECG分类准确性和泛化性的重要手段，已成为当下的研究重点。

ECG信号是一种微弱的准周期信号，个体体质差异以及生理和心理条件的变化，都会导致同一种心律类型的ECG信号，在不同个体上的形态特征也不尽相同。为了能更好地提取出ECG的特征，国内外学者开展了很多研究。文献[2]使用图形正则化非负矩阵分解（GNMF）构造一个亲和图，对心电信号的几何信息和标签信息进行编码，然后采用稀疏表示提高心电信号的分辨率，从而提取出更具鉴别能力的特征。文献[3]采用二维主分量判别法（2D-PCA）对12导联高频ECG信号进行融合特征提取，将2D-PCA和能量百分比法结合起来融合信息，提取出HF-ECG的全局特征和本征向量，最后用基于均方差属性加权的改进遗传模拟退火K-means算法完成心电分类，达到93.61%的准确率。深度学习因为其可自动抽取样本特征，相比于传统的人工设计特征方法优势突出，逐渐活跃于ECG特征提取的研究领域中。文献[4]以高斯-伯努利受限玻尔兹曼机构建六层深度信念（DBN）网络抽取10维心电信号的高层抽象特征为数据基础，采用FCM进行特征分类，总准确率达96.54%。文献[5]以堆叠式降噪自编码器（SDAEs）进行ECG降噪、自编码器（AEs）提取特征与卷积神经网络（CNN）分类构建八种ECG深度学习模型，其中最优模型的识别率达到了99.34%。文献[6]采用自适应一维CNN提取信号特征和分类，能大幅提高诊断速度和计算效率，但需要为特定病人训练单个的CNN，普适性得到限制。

心电信号的特征提取方式没有统一标准，主要包括波形形态特征、时频域特征以及高阶统计特征等。ECG分类模型分为传统机器学习和深度学习，其中传统机器学习依赖于特征工程，心电信号特征选择缺乏标准化，特征为人工设计，需要领域相关知识，且单一特征不能较为全面地反应ECG信号的全部病理信息，多特征方式能有效提高分类模型的准确率，但是会增加时间复杂度，对心电信号的质量要求较高，低质量的波形信号可能造成源信号特征信息丢失的问题[7]。深度学习模型用于ECG特征提取准确率较高，可解决有效特征难人工提取的问题，但需要大量的训练有标签样本，目前的ECG信号样本的标注需要专业的心电图医生进行，在数据量非常大的情况下，对数据进行标注是一件困难的事情。国内外使用最广的MIT-BIH数据库收录了40种不同类型的心律失常样本，但仅有少数类型的样本具有较为丰富的数量，多数样本数量无法达到机器学习模型训练的标准。自编码器以神经科学为支撑点，延续了深度学习的优点，以自监督的方式，从大量无标签的数据中自动学习到数据的有效特征，更加接近人类大脑思维方式，通过前向预训练和反向微调使其具有很好的特征自学习能力和泛化能力，具有重建简单，可多层堆叠的优点，已广泛应用于模式识别、异常检测、图像分类、自然语言处理等领域当中[8]。因此本文提出基于深度稀疏自编码器的ECG特征提取方法。将ECG数据输入深度稀疏自编码器，灵活调整隐含层数和单元，通过逐层训练提取原始ECG数据的特征表达，得到适合ECG特征提取的DSAEs结构，预训练和模型微调阶段都使用了Adam算法进行参数寻优，最后采用SVM进行ECG特征分类。实验验证了该方法自动提取的ECG特征提高了分类模型的性能，且适应性更强，识别率达到98.57%。

1 深度稀疏自编码器的特征选择算法

1.1 深度稀疏自编码器

深度自编码器（DAEs）是由若干自编码器（AEs）堆叠形成的浅层自编码网络。AEs是深度学习中的一种非常重要的无监督学习方法，通过增加隐含层数量，进行贪婪逐层预训练，从高维的训练数据中分层地提取输入数据的特征，可以学习到更多能够表示数据隐含特征的抽象知识[8]。

深度稀疏自动编码器（DSAEs）则是通过添加稀疏约束项来对隐含层进行稀疏性约束，可以改善发现数据隐藏结构的性能，对数据有一个更好的重构结果，同时加快模型收敛[9]。

DSAEs编码解码过程可描述为：

其中，f和g分别称为编码器和解码器映射，σ为激励函数，W∈RD×d为编码权重矩阵，b∈RD为编码偏置向量，W′=WT为解码权重矩阵，b′∈Rd为解码偏置向量。SAEs的训练目标是优化参数集θ={ }W,W′,b,b′，使得重构误差最小。

1.2 基于DSAEs的ECG特征提取

对于输入ECG数据x={x1,x2,…,xT+D}，T代表训练样本，D代表测试样本。标签向量为Y=[Y1,Y2,…,Yc]，c代表ECG标签数量，Yi取值为1或0，代表是否属于第i类ECG类型。

选用Sigmoid为激活函数，均方误差为损失函数，DSAEs的误差函数表达式如式（3）：

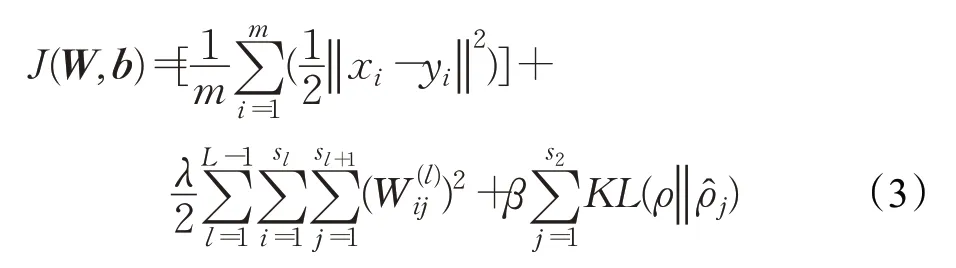
等式右边第二项为正则项因子，用于抑制静态噪声对目标和权重向量中不相关成分的影响，避免模型过度拟合，λ表示控制约束项比例的权重衰减参数，L为网络层数，sl为第l层的单元数量，为l层第i个单元与l+1层第j个单元间的权重值，为稀疏惩罚项，β为惩罚系数，K L为散度，表达式见式（4），ρ为稀疏参数，其值常被设置为接近0，表示第j层隐含层单元的平均激活函数。

DSAEs隐含层的输出为所提取到的ECG抽象特征，特征向量的表达式为：

1.3 基于DSAEs参数优化的学习算法（DSAEs-Adam）

在DSAEs网络模型训练中，常采用随机梯度下降法（SGD）调整权重矩阵和偏置向量，梯度下降法的数学公式如下[10]：

其中，η为学习率，SGD在自调节编码器各层权值时，保持单一学习率，在训练过程中不会改变，且对于不同参数具有相同学习率，使得模型收敛速度慢，收敛精度低，影响最终结果。针对此问题，本文利用适应性矩阵估计（Adam）算法来进行参数的更新优化。Adam算法是一种结合了Adagrad和RMsprop算法的一阶优化算法[11]，通过计算梯度的一阶矩估计和二阶矩估计而针对不同的参数设计独立的自适应性学习率，调参少，计算高效，所需内存少，能减少神经网络收敛时间，梯度对角缩放具有不变性，适用于高维空间和大数据集。Adam算法的伪代码如下所示。

算法 适应性矩阵估计算法（Adam）

输入：学习率η，一阶矩的指数衰减率β1，二阶矩的指数衰减率β2，数值稳定小常数ε，目标函数L及其参数θ

2 支持向量机深度稀疏自编码网络的ECG特征提取分类模型

2.1 支持向量机（SVM）

本文通过构建多个二分类器，将SVM的二分类问题拓展到多分类。采用高斯径向基核函数作为支持向量机的核函数，通过遗传算法对支持向量机寻优后的惩罚因子c为2.863 3，核参数g为4.542 3。

2.2 支持向量机深度稀疏自编码网络实现步骤

本文提出的基于深度稀疏自编码的ECG特征提取算法的流程如图1所示。图中红色框的隐含输出即为提取出的ECG高度抽象特征。

DSAEs的层数和单元数要根据ECG信号采样数据L，标签向量Y等来调整。算法实现步骤如下：

输入：训练样本集ds_tr aining=，测试样本集ds_testing，Adam算法参数

输出：隐含层表示、参数θ

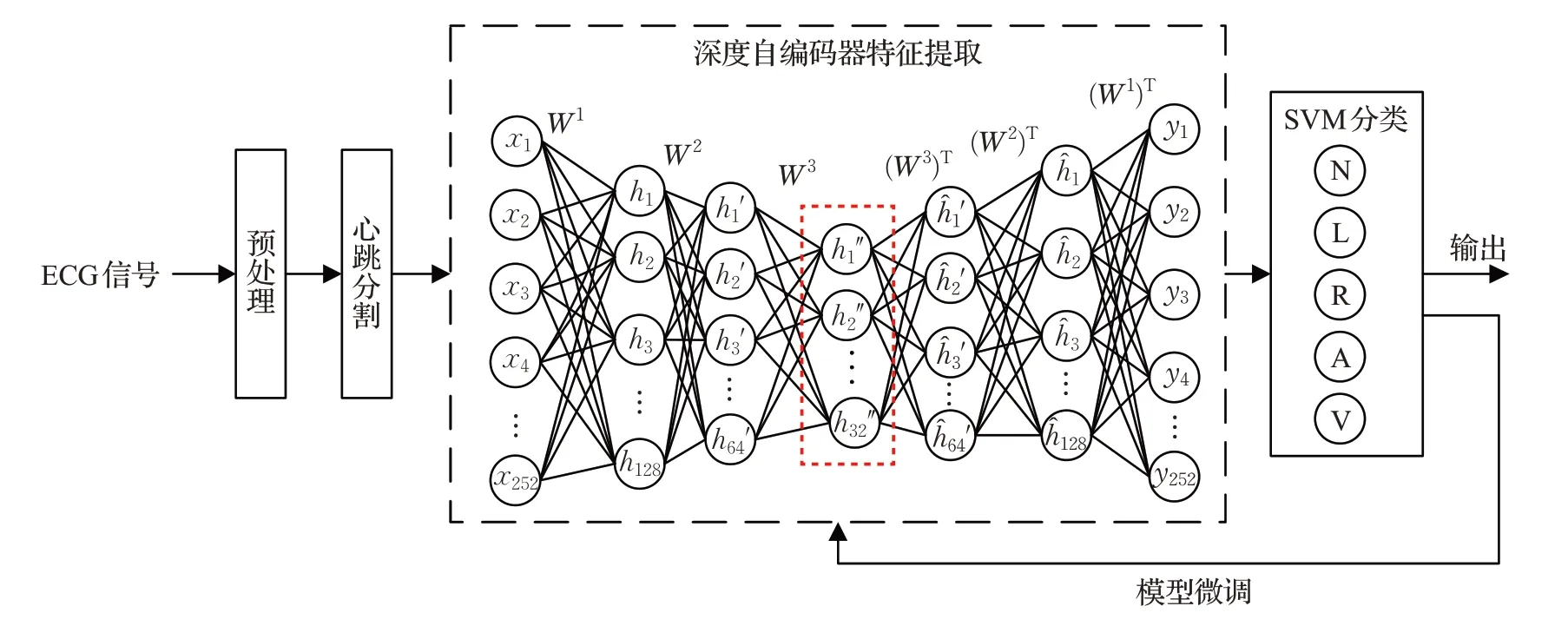
图1 本文算法流程图

步骤1随机初始化权重矩阵和偏置向量。ECG样本进行前向传递，得到输出层y。

步骤2最小化公式（3），利用Adam算法更新参数θ。

步骤3根据更新参数计算隐含输出表示hl。

步骤4将hl作为输入传递给下一层，重复步骤1、2、3，直至贪婪无监督学习完所有隐含层。

步骤5根据式（5）进行有监督学习，获取训练的ECG样本高层抽象特征。

步骤6支持向量机进行分类。

步骤7利用XL,Y，结合反向回馈算法、Adam算法进行微调，实现模型优化。

步骤8采用测试样本ds_testing进行分类。

3 实验与结果分析

3.1 实验数据

实验数据来源于MIT-BIH心律异常数据库[12]，包含48条时长为30 min的ECG记录，共计18种专家注释的心跳类型，109 655个心拍，采样频率为360 Hz，其中有25条记录包含复杂心律失常类型，23条包含常规性心律失常类型，可作为临床代表性样本。

本文主要分析以下五种心律类型，包括正常(N)、左/右束支传导阻滞(L/R)、房性早搏(A)和室性早搏(V)。实验采用编号为100、105、111、114、116、118、201、203、207、210、213、215、228、232的ECG记录为训练集，测试集的ECG记录编号为103、106、109、205、209、214、223、231，实验数据集如表1所示。

表1 实验数据集

数据库中不同记录对象具有不同的心跳频率，DSAEs采用统一长度的ECG信号作为输入。为了让输入的信号包含完整的QRS波群，本文取R波波峰前t1=0.25 s和R波波峰后t2=0.45 s，共计0.7 s片段作为一个完整心拍，如图2所示。

图2 心拍切割

3.2 实验参数与评价指标

本实验中，实验仿真在Intel Core i5-3230M，CPU主频为2.6 GHz，64位Window10操作系统MATLAB2016a下完成。实验采用“训练-测试”模式进行ECG信号的识别分类。ECG预处理参考文献[13]的处理方式。深度稀疏自编码器的输入层单元数为252（0.7×360），接收统一长度的ECG连续信号，权重衰减参数λ=0.000 1，稀疏参数ρ=0.05，惩罚稀疏β=3，学习率η=0.001，一阶矩指数衰减率β1=0.9，二阶矩指数衰减率β2=0.999 9，常数稳定值ε=10-8。

本文采用灵敏度(Se)、阳性预测值(Ppv)、F1值以及总正确率(Acc)四种指标对实验结果进行评估，计算方法如下：

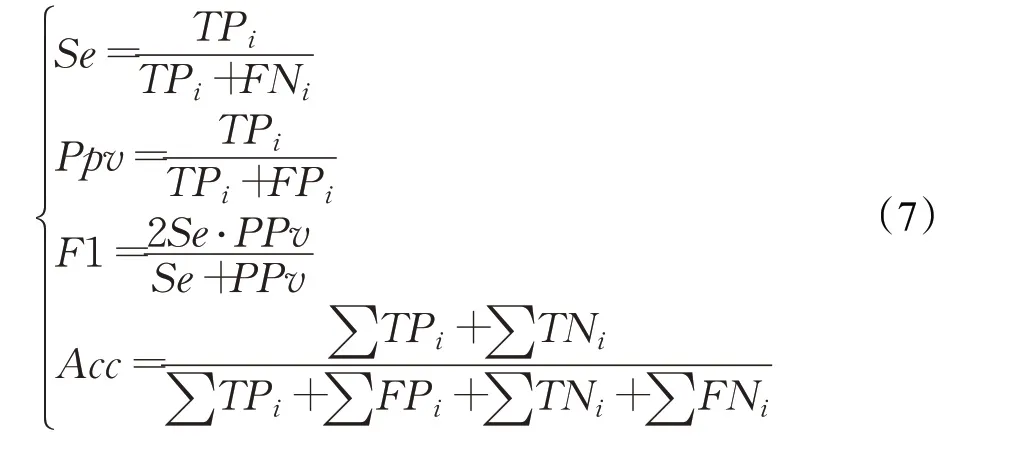
TPi为正确分到i类心拍个数，TNi表示不为i类的心拍被正确分开个数，FPi为不属于i类心拍被分到i类心拍的个数，FNi表示i类心拍错误分到其他类的个数。

3.3 实验结果与分析

深度稀疏自编码器的网络结构需要逐层确定，本文对深度稀疏自编码器网络中隐含层层数、特征维数与五种心律识别效果的关系做了实验。

图3为最简单的三层稀疏自编码器（输入输出层节点数为252），通过增减隐含层节点数，分别进行了14次实验。

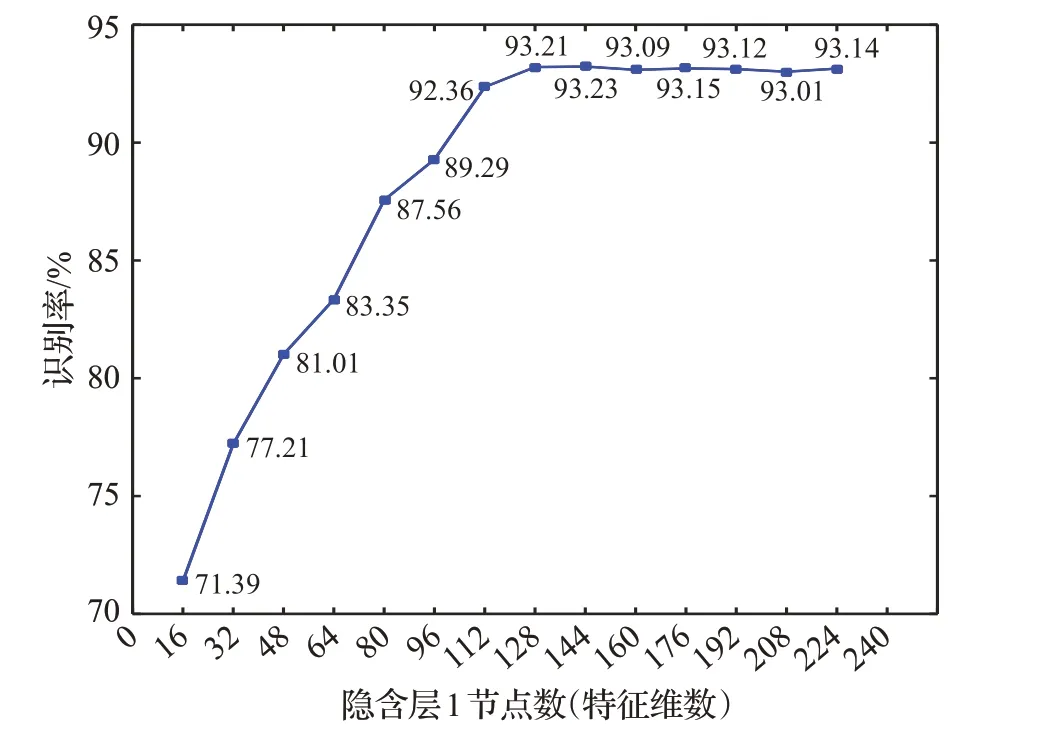
图3 隐含层1节点数与识别率的关系

从图3中可以看出，在单层隐含层上，随着隐含节点数的增加，模型识别率逐渐提高，当隐含节点数在128的时候，识别率达到93.21%，继续增加隐含节点数，模型识别率波动不大。这是因为当隐含节点数过少时，隐含节点对原始输入进行压缩，不利于对原始数据进行特征提取。当隐含节点数较多时，自编码器可能将输入复制到输出或学习到恒等函数，从而无法学习到数据的有效特征，本文通过添加稀疏性限制，使得多数神经元处于抑制状态，迫使神经元学习到数据真正的特征，因此能在隐含节点数继续增加时保持较高的识别率。考虑到简化编码器网络结构减轻计算负担，因此设定隐含层1的节点数为128。

同理，本文对隐含层2、3、4的隐含节点数进行了实验。图4为稀疏自编码器隐含层2的节点数与识别率的关系图。通过增减隐含节点数目，分别进行了15次实验。

图4 隐含层2节点数与识别率的关系

从图4中可以看出，随着节点数的增加，模型识别率逐渐提高，在隐含节点为64时，识别率最高为95.39%，隐含节点大于64时，识别率在95%左右波动，因此设定隐含层2的节点数为64。

图5为隐含层3节点数与识别率的关系。通过增减节点数目，分别进行了14次实验。

图5 隐含层3节点数与识别率的关系

从图5中可以看出，经过叠加三个稀疏自编码器，模型识别率大大提高。在隐含层3节点数超过28个时，模型的识别率超过98%，在36和44个节点时，识别率最高为98.35%，本文设定隐含层3的节点数为36。

图6为隐含层4节点数与识别率的关系。在上一个自编码网络结构的基础上，进行了7次实验。

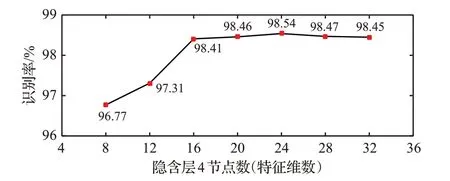
图6 隐含层4节点数与识别率的关系

从图中可以看出，在隐含节4的节点数为24时，模型的识别率最高为98.54%。此时深度稀疏自编码器的网络结构为（252-128-64-36-24-36-64-128-252）。

为了验证本文中采用Adam算法进行参数寻优的有效性，将DSAEs-Adam和DSAEs-SGB，在相同结构和参数下进行训练和微调。实验结果见表2。

表2 参数优化算法识别率对比%

表2显示了两个模型在不同隐含层单元上的识别率，可以明显看出，DSAEs-Adam模型的识别率均高于DSAEs-SGB模型，原因在于Adam算法针对不同参数自适应性学习率，提高模型的收敛精度。

图7 测试数据集上的心律分类结果混淆矩阵

图7是在测试数据集下，应用上述识别率最高的编码网络结构（252-128-64-36-24-36-64-128-252）得到的五种心律失常结果的混淆矩阵，根据式（7）计算出每种类型下的灵敏度、阳性预测值、F1值及总体准确率，如表3所示。

从图7中可以看出，本文提出的方法在N-V上的混淆值最大（30），可能造成的原因为数据集的极度不平衡，在测试数据集上，室性早搏（V）的数据量为正常心律（N）数据量的7.7%，占总数据量的4.6%。此外由于本文主要集中在单导联分析上，在某些情况下，不同病症的单拍特征可能出现相似，由此造成较大的混淆值。

表3 性能指标

表3显示出DSAEs-Adam能有效识别出五种心律类型，且都有较好的划分结果，对正常（N）类型的心律灵敏度达到99.24%，总正确率达到98.57%。为了进一步评估所提方法的有效性，本文将DSAEs-Adam与其他特征提取研究结果进行对比，对比结果见表4。

表4 与其他研究结果的对比

表4中，文献[14]应用经验模态分解提取出信号的固有模式函数作为特征集，通过多次实验，应用遗传算法选出最优特征子集；文献[15]应用多种特征提取方法，分别提取出波形形态特征、形态学距离以及QRS波群的主成分分量，因此获取较高的识别率。文献[16-17]中都应用了小波变换，文献[17]应用多相表示生成新的小波，并采用粒子群算法选择最优小波，但由于没有考虑PSO的早熟问题，且提取出的特征维数较少，导致模型的整体识别率偏低；文献[16]应用改进小波提取出QRS波群和P/T波的高维特征，并采用人工蜂群算法优化分类器，因此模型的识别率显著提高。本文堆叠了四个稀疏自编码器，通过多次实验，逐层确定隐含节点数，得到适合ECG特征提取的DSAEs结构，利用逐层贪婪训练，提取出心电信号的特征表达。本文方法与其他特征提取方式相比，识别率都有一定的提高，说明经过深度稀疏自编码器提取的特征能更好地反映ECG心跳特点。实验中，训练数据和测试数据来自不同的数据集，表明本文方法具有较好的适应性。

4 结语

针对ECG智能分析模型中，ECG形态复杂，导致特征提取困难，人工设计特征，识别率不高，缺少标签数据等问题，本文将深度稀疏自编码器应用在ECG特征提取上。该方法采用DSAEs对连续心电信号进行贪婪逐层训练，利用Adam算法对参数进行寻优，找出每一隐含层最佳节点个数，提取出高层隐含层的输出，作为心电信号的特征向量，然后结合SVM构建心电分类模型。仿真实验结果表明，本文所提出的方法分类准确率更高，模型适应性更强，在隐含层数为7，特征维度为24时，识别率最高达到98.57%。本文所提出的特征提取和分类方法可以应用到其他类似生物信号处理上，未来工作可深入研究其他深度学习特征提取方法和分类算法相结合在生理信号自动分类中的应用，为可穿戴式多体征生理信号监护系统实现自动监测分析作参考。