犹豫模糊群共识实现算法及其数据系统优选
陈雪娟
广东理工学院 信息技术学院,广东 肇庆526114
数据库系统一般由数据库、数据系统、数据应用系统、数据库管理员和用户构成[1-2]。数据库系统的核心和基础是数据系统,现有的数据库系统均是基于某种数据系统设计构造的。因此,在数据库系统的管理过程中,如何选择数据系统至关重要,其本质上是在多个评价指标下对备选的数据系统进行两两比较,并由专家给出评价信息,这样的过程本质上是一个群决策过程。
群体决策(Group Decision Making,GDM)作为现代社会管理活动的一个重要组成部分,在各个领域有着广泛的应用[3-4]。由于主客观因素的影响,学者们运用偏好关系来描述模糊信息[5]。模糊偏好关系[6]和乘性偏好关系[7]是描述决策者评价信息的两类最常见的偏好关系形式。之后,直觉模糊偏好关系[8]、毕达哥拉斯模糊偏好关系[9]、区间值偏好关系[10]被相继提出。作为偏好关系的一类重要扩展,犹豫模糊偏好关系(Hesitant Fuzzy Preference Relation,HFPR)[11]可以全面地描述专家给出的评价信息,可以提升复杂环境下决策结果的可靠性。
针对不同的偏好关系,一致性算法和共识性模型是两个最重要的研究课题,其可以确保最终的群决策结果的科学有效。Herrera-Viedma等[12]提出了构造一致模糊偏好关系的方法。对于具有区间模糊偏好关系的GDM问题,Zhang[13]利用多种数学规划算法提出了新的GDM方法,并确定了方案的排序结果。对于应急管理评估问题,Jin等[14]提出了基于直觉模糊偏好关系的GDM方法来评估应急操作中心的综合性能。Meng等[15]建立了一系列整数优化模型来提升一致性水平并估计缺失信息,然后研究了GDM方法来处理不完全和不一致的直觉模糊偏好关系。Zhang等[16]研究HFPR环境下的GDM方法,包括一致性调整算法、共识达成方法和方案排序方法。Zhu等[17]设计新的优化模型和一致性改进算法从HFPR中生成优先级权重向量。分析发现,现有针对HFPR的研究主要集中在一致性的检验和改进算法方面。
事实上,一致性算法主要用于衡量各个决策者提供的HFPR信息内部的一致性程度,而共识性模型主要用于衡量决策者提供的HFPR之间对备选方案评价的一致性程度,其对最终的群决策结果的可靠性至关重要。因此,本文首先引入了新的HFPR一致性指数计算公式,并在群体环境下设计了犹豫模糊群共识实现算法,同时验证在群体共识实现算法结束后,修改后的HFPR序列不仅达到了预定的共识性水平,而且保持了原先的一致性水平。最后将本文提出的算法应用于银行购买数据系统的选择评价过程中。
1 HFPR及其一致性
本章首先回顾HFPR及其一致性的基本概念,然后提出一种新的一致性指数公式用于衡量HFPR一致性水平。令X={x1,x2,…,xn}为待评估的一组备选方案集合N={1,2,…,n}。在评估过程中,由于评价问题的复杂性,专家对备选方案进行分析比较的过程中,借助于文献[4]中的方法,可以得到具有相同元素个数的犹豫模糊元(Hesitant Fuzzy Element,HFE)来描述评价信息,从而构建出如下的HFPRF=(fij)n×n。
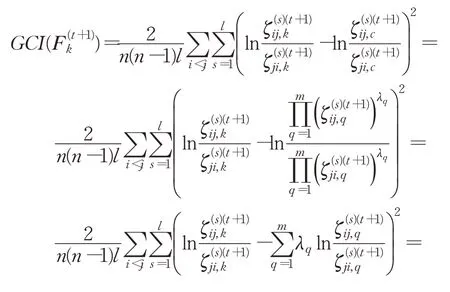
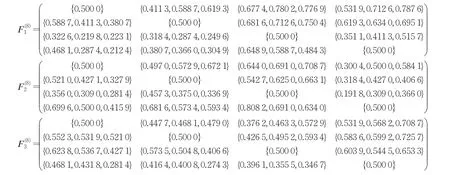
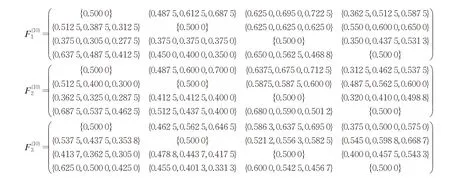
定义1[11]定义在方案集X={x1,x2,…,xn}上的矩阵F=(fij)n×n称为HFPR,若对∀i,j∈N且当i 通过定义1可知,HFPRF=(fij)n×n上三角HFE中的元素单调增加,下三角HFE中的元素单调递减。接下来,介绍HFPR乘性一致性的概念。 定义2[16]定义在X={x1,x2,…,xn}上的HFPRF=(fij)n×n,若对∀i,j,q∈N,有: 则称HFPRF=(fij)n×n具有乘性一致性。 运用文献[18]中的如下方法: 可构造出具有完全乘性一致性的HFPRF͂=(f͂ij)n×n。 为了衡量HFPRF=(fij)n×n的一致性水平,引入如下的一致性指数公式: 定义3令F=(fij)n×n是一个HFPR,则F的一致性指数CI(F)定义如下: 对于复杂的群体决策问题,还需要考虑专家给出的评价信息之间的共识性。若专家群体共识程度高,则最终的群决策结果越可靠;专家群体共识程度低,则得到的群决策结果可靠性就越低。因此,本章将构造犹豫模糊共识实现算法。假设E={e1,e2,…,em}表示为评估专家集合,其对应的权重向量为λ=(λ1,λ2,…,λm)T,M={1,2,…,m},满足λk≥0,k∈M=1。在评估过程中,专家ek对备选方案集中的方案进行两两比较,从而构造出HFPR序列Fk=(fij,k)n×n(k∈M),其中s=1,2,…,l}。 针对专家群体给出的HFPR序列Fk=(fij,k)n×n(k∈M),令Fc=(fij,c)n×n,fij,c=且: 定理1令Fk=(fij,k)n×n(k∈M)是一组HFPR序列,则通过公式(5)得到的矩阵Fc=(fij,c)n×n是综合HFPR。 证明首先,显然有,=0.5,且: 其次, 因此,根据定义1可知,矩阵Fc=(fij,c)n×n是一个综合HFPR。 定理2令Fk=(fij,k)n×n(k∈M)是一组HFPR序列,Fc=(fij,c)n×n是通过公式(5)得到的综合HFPR,则有。 证明设,则有: 综上,定理2得证。 由定理2可知,当Fk(k∈M)均为满意一致性HFPR时,那么综合HFPRFc=(fij,c)n×n也具有满意一致性;当Fk(k∈M)均为完全一致性HFPR时,那么综合HFPRFc=(fij,c)n×n也具有完全一致性。 群共识实现过程中一个重要指标是判断群体共识水平是否达到了给定阈值。因此,引入下面的群共识指数概念。 定义4令Fk=(fij,k)n×n(k∈M)是一组HFPR序列,Fc=(fij,c)n×n是通过公式(5)得到的综合HFPR,则Fk的群共识指数GCI(Fk)定义如下: 显然GCI(Fk)≥0,并且GCI(Fk)越小,则表示专家ek的共识水平越高。当GCI(Fk)=0时,说明专家ek达到了完全共识水平。 为了从群体HFPR中得到合理的决策结果,要求专家们提供的所有HFPR都是具有满意一致性和共识性。然而,由于人类思维中固有的模糊性,在实际的GDM问题中,专家们较难提供这样的HFPR序列。因此,如何提升HFPR的一致性和实现群体共识在群决策过程中是非常重要的。为了解决这一问题,本文设计如下的犹豫模糊群共识实现算法,从而得到更为合理可靠的群决策结果。 算法1 输入:群体专家E={e1,e2,…,em}提供的HFPR序列Fk=(fij,k)n×n(k∈M),专家权重向量λ=(λ1,λ2,…,λm)T,一致性指数阈值,群体共识指数阈值,一致性调整参数δ∈(0,1),共识性实现调整参数η∈(0,1)。 输出:综合性能最高的方案x͂。 步骤1令(k∈M),t=0。运用公式(3)构造出具有完全乘性一致性的HFPR序列。 步骤2运用公式(4)计算一致性指数,并判断HFPR序列的一致性水平。若,则执行步骤4;否则执行步骤3。 步骤3对的HFPR进行调整: 步骤4利用公式(5)将具有满意一致性的HFPR序列融合成一个综合HFPR 步骤5通过定义4计算HFPR的群共识指数,并判断HFPR序列的共识性水平。若,k∈M,则执行步骤7;否则执行步骤6。 步骤6对的HFPR进行如下的共识性调整: 步骤7令。基于得到的综合HFPRFc=(fij,c)n×n,对每一行元素进行集成: 从而得到备选方案xi(i∈M)对应的综合HFE1,2,…,l}(i∈M)。 步骤8计算HFEfi,c(i∈M)的得分函数: 并依据得分函数的大小对备选方案集进行排序,从而筛选出最佳方案x͂。 下面通过两个定理来说明算法1的优良性质。 定理3假设是HFPR序列,是通过共识调整公式(9)得到的HFPR序列,则有: 证明由于是运用公式(9)调整得到的新HFPR,则有: 定理3说明了如果原始的HFPR序列都是完全乘性一致性或具有满意一致性,那么通过犹豫模糊群共识实现算法1进行调整后的HFPR序列仍是完全乘性一致性或具有满意一致性。 定理4假设是HFPR序列,是通过共识调整公式(9)得到的HFPR序列,则有: 证明根据公式(5)、(7)和(9)可得: 综上,定理4得证。 定理4说明了通过犹豫模糊群共识实现算法1进行调整能够提升HFPR序列的共识性水平。 本章将运用设计的犹豫模糊群共识实现算法1处理数据系统的选择问题,并通过对比分析实验来验证算法1的有效性。 随着城市化水平的大幅度提高和人口总量的不断增加,人们产生的数据规模以指数级的速度增加,而数据信息量巨大是困扰银行进行及时信息处理的顽疾,因此银行系统需要及时更新和升级数据系统,否则将会造成交易数据处理不及时、数据存储量不够、交易数据信息丢失等后果。某国有银行因为原有的数据系统年代已久,处理数据信息的速度降低,造成业务办理效率低下,现需要对原有的数据系统进行更换和升级。该银行的采购部门在对市场上数据系统的价格成本、综合性能、售后服务、系统可持续性等指标进行考察后,筛选出来四套备选的数据系统{x1,x2,x3,x4}。为了筛选出一套综合性能最佳的数据系统,该银行邀请了3个相关方面的专家和工程师{e1,e2,e3}依据上述指标对备选的四套数据系统进行两两比较,3个专家的权重向量为λ=(0.2,0.5,0.3)T。由于数据系统中存在一些不精确信息和专家的专业存在差异性,专家们很难给出精确的偏好判断矩阵,因此专家们运用HFPRFk=(fij,k)n×n(k=1,2,3)来描述他们的评价信息,具体如下: 步骤1令=1,2,3,并运用公式(3)得到对应的完全乘性一致HFPR(k=1,2,3)(由于篇幅限制,则不列出)。 步骤2根据公式(4)计算一致性指数分别为: 步骤3由于,因此需要运用公式(8)对进行一致性调整。经过8次迭代之后,可得具有满意一致性的HFPR: 它们的一致性指数分别为: 步骤4~步骤6通过公式(5)将融合成综合HFPR,并通过公式(7)计算的群共识指数分别为: 并利用公式(5)将HFPR序列 步骤7令。运用公式(10)对Fc的每一行元素集成为如下的综合HFE: 步骤8借助于公式(11)得到fi,c(i=1,2,3,4)的得分函数值分别为: 由于Θ(f1,c)>Θ(f2,c)>Θ(f4,c)>Θ(f3,c),那么四套备选数据系统的综合性能排序为:x1≻x2≻x4≻x3,于是建议该银行采购部门购买的数据系统为x1。 为了说明本文提出模型的有效性,下面将运用文献[17]中的算法处理上述问题。文献[17]中的算法首先运用得分函数将原始的HFPR序列转化为对应的期望模糊偏好关系序列,再根据一致性调整算法来对模糊偏好关系序列进行一致性的检验和改进,最后将专家赋予相同的权重来对改进后的模糊偏好关系序列进行集成,从而得到下面的综合模糊偏好关系: 在运用信息集成算子对每一行元素进行融合后,可以得到四套数据系统的综合性能排序为:x1≻x2≻x3≻x4,从而得到综合性能最佳的数据系统为x1。进行优选排序,具体群决策过程如下: 步骤1计算三个HFPRFk=(fij,k)n×n(k=1,2,3)对应的得分函数矩阵Δ(Fk)(k=1,2,3): 根据三个得分函数矩阵Δ(Fk)(k=1,2,3)可知,三个HFPRFk=(fij,k)n×n(k=1,2,3)均不满足有序一致性,因此转入下一步。 步骤2以HFPRFk=(fij,k)n×n(k=1,2,3)为基础,通过文献[19]中的模型(7)计算得到三个HFPRFk(k=1,2,3)对应的非负偏差变量分别如下: 从而可知三个HFPRFk(k=1,2,3)对应最优化模型的目标函数值均不为0,即它们的一致性指数分别为CI(F1)=0.758 0,CI(F2)=0.602 0,CI(F3)=0.473 1。由于CI(Fk)>=1,2,3,所以原始三个HFPRFk(k=1,2,3)不具有满意乘性一致性,因此转入下一步。 步骤3借助于HFE的得分函数和文献[19]中的公式(8)对原始三个HFPRFk(k=1,2,3)进行一致性调整和改进,并运用公式(5)得到满足基于得分函数乘性一致性的综合HFPRH如下: 步骤4根据文献[19]中的模型(9)和模型(10),计算出四套数据系统的排序权重分别为: 步骤5根据计算出的排序权重大小得到四套数据系统综合性能排序为x1≻x4≻x2≻x3,于是运用文献[19]中算法2得到综合性能最佳的数据系统也为x1。 对比文献[17]和文献[19]中的群决策方法过程和群决策结果,发现本文算法存在以下优势:(1)文献[17]将相同的权重分配给每个专家,忽略了不同的专家在GDM中所扮演的角色不同而具有不同重要性的情况。相比之下,在本文方法中,不同的专家具有不同的权重。(2)文献[17]研究了HFPR所对应的期望模糊偏好关系的一致性改进算法,这些期望模糊偏好关系不完全等同于原始的HFPR,因此期望的模糊偏好关系忽略了原始HFPR的犹豫。相比之下,本文算法都是基于原始HFPR进行的一致性改进和共识性水平的提升,因此充分利用专家原始偏好信息的犹豫性和不确定性。(3)文献[19]中算法2在判定一致性过程中依据原始HFPR的得分函数矩阵进行判定,其不能充分地反映原始决策者的评价信息。而本文的群决策过程均是直接使用原始HFPR进行决策,因此决策结果更为可靠。(4)文献[17]和文献[19]基于HFPR满意加性一致性进行决策分析。正如文献[14]所指出的,HLPR的加性一致性定义是不合理的,而乘法一致性是HFLPRs更理想的选择。相比之下,本文提出的基于HFPR的GDM方法的优点是遵循了满意乘法一致性和群体共识性水平。例如,根据具有满意一致性的HFPRF(8)k(k=1,2,3)可知,其中的第四行元素整体上高于第三行元素,从而说明了数据系统x4的综合性能应高于数据系统x3,这与本文算法得到的群决策结果相同,从而验证了本文算法是有效的。 本文提出了一种基于犹豫模糊群体共识算法的GDM方法。首先,本文引入了一种新的一致性指数用于衡量HFPR的一致性水平;随后,建立了犹豫模糊群共识实现算法,并验证了算法的收敛性和其他优良性质;最后,通过数据系统选择的实例说明了本文方法的实际应用,并进行了对比分析。从实验结果可以看出,本文方法得到的结果更为合理有效。事实上,本文提出的犹豫模糊群共识实现算法考虑了犹豫模糊决策的整个过程,包括一致性提升、共识性实现以及最佳方案选择,而现有的模糊语言决策方法大多只关注一个或两个过程。因此,本文提出的GDM方法可以很好地处理实际的群决策问题。但是在本文算法的构建过程中缺乏对群体专家之间的交互情况进行考虑,同时在算法初始化过程中,均是对群体共识指数阈值和共识性实现调整参数进行了主观赋值,没有探究群体共识指数阈值和共识性实现调整参数的变化是否会对最终的群决策结果产生影响。因此,下一步将深入探究和分析群体共识指数阈值的变化对群决策结果的影响机理,并对共识性实现调整参数进行灵敏度分析,另外,将考虑群体专家之间的内在联系来设计犹豫模糊群体协同决策模型。



2 犹豫模糊群共识实现算法的设计
2.1 综合HFPR的构造

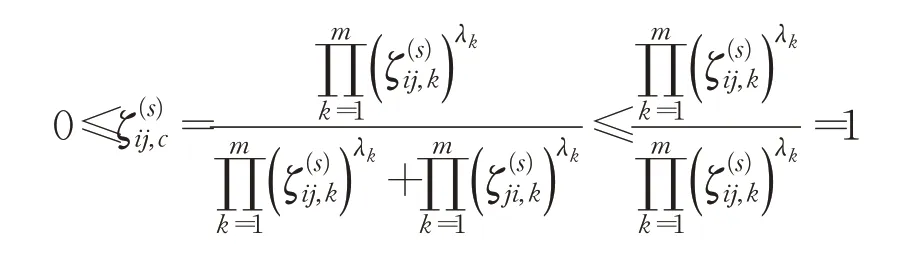
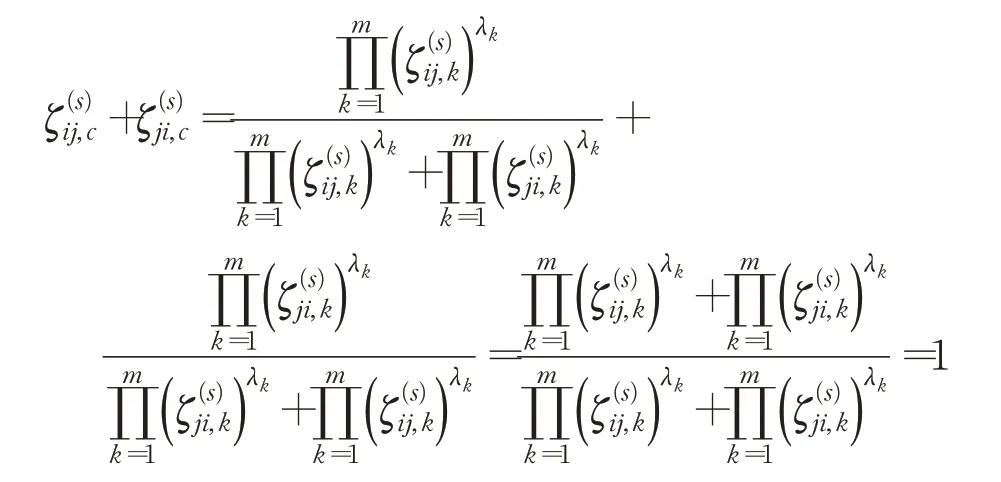

2.2 犹豫模糊群共识实现算法的建立
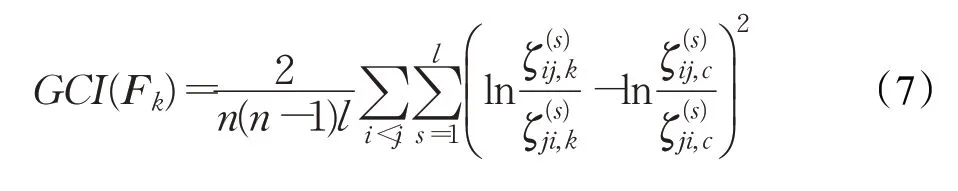
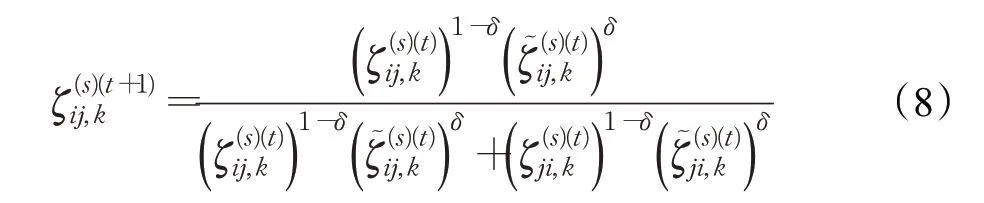
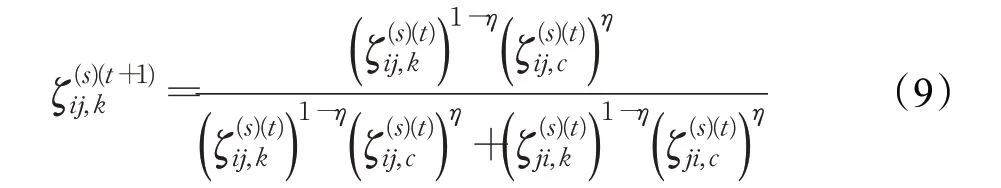
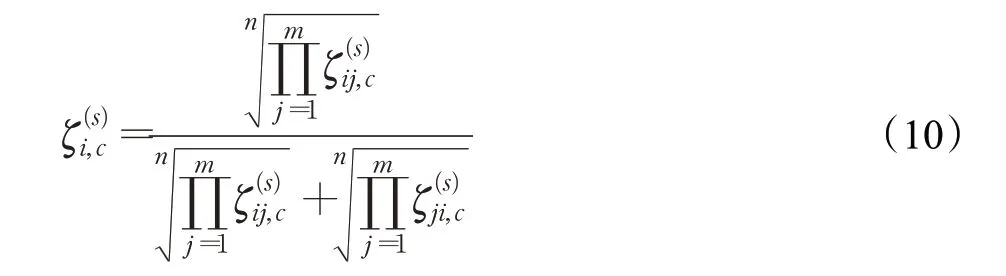
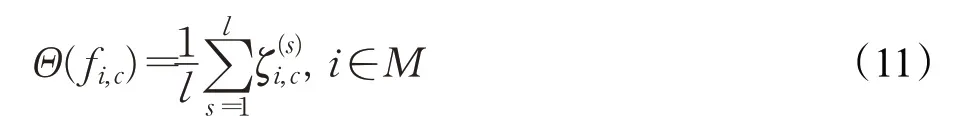

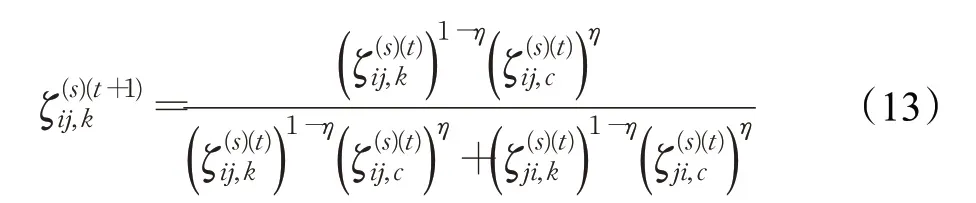



3 实验分析
3.1 算例分析









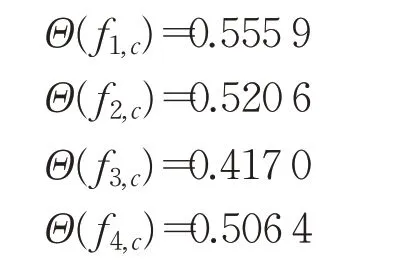
3.2 对比分析





4 结束语

