基于改进自回归流模型的坝基三维裂隙网络多参数模拟
张亦弛,吕明明,关 涛,王佳俊,余 佳,任炳昱
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
1 研究背景
对于水电工程坝基裂隙岩体,探明其内部的裂隙发育情况能够为坝基工程地质分析与决策提供关键依据,对于保障水电工程的安全稳定具有重要的理论与现实意义[1-3]。裂隙是指岩石受到构造变形的破裂作用或物理成岩作用形成的没有明显位移的面状不连续体[4],在岩体内部常呈现网状分布。离散裂隙网络(Discrete Fracture Networks,DFN)模型是由Baecher 等[5]提出的一种研究裂隙空间展布的有效手段,该方法将每一个裂隙表达为一个具有厚度的圆盘模型。基于从岩体表面露头与内部钻孔中观测的裂隙先验信息,通过示性点过程进行裂隙网络随机建模,其中点过程基于稳态泊松过程确定裂隙中心点的位置[6],示性过程确定裂隙的属性,即圆盘裂隙的几何参数[4]。
三维离散裂隙网络模型本质上是对岩体内裂隙的倾向、倾角、直径、开度等属性特征联合分布的几何表达[4,6],因此,裂隙网络的多参数模拟是目前的研究趋势[6-8],其关键问题在于对裂隙的几何参数之间的多维联合分布进行概率密度估计与采样。现有的DFN 建模方法通常假设裂隙的几何参数之间互相独立,并采用典型分布对每个参数的边缘分布进行概率密度估计(Probability Density Estima⁃tion)与采样(Sampling),例如:描述直径与迹长的Gamma 分布与对数正态分布、描述开度的负指数分布与对数正态分布、描述走向的Von-Mises 分布等[4,6,9]。Mendoza-Torres 等[10]的研究指出现有DFN建模研究通常采用的单参数模拟方法忽略了裂隙几何参数之间可能存在的相关性[10],当实测裂隙参数之间不独立时,分别从各边缘分布中抽样的结果不一定会服从联合分布,相反,直接对联合分布进行估计的方法自然地考虑了参数之间的相关性[10]。然而,传统的DFN 建模方法仅针对倾向与倾角参数考虑了联合分布估计的问题,且仍然采用典型分布假设,包括:Fisher 分布、双正态分布、Bing⁃ham 分布、Kent 分布等[6,11]。事实上,由于岩体内部裂隙发育的内在规律十分复杂,工程实测数据中三个以上裂隙几何参数的联合分布一般不符合上述几种典型分布中的任何一种[10],此时基于典型分布的估计方法缺乏足够的拟合能力[10],且严格的分布类型假设可能带来偏倚与误差[10-11]。综上,目前的DFN 建模方法面临着难以有效拟合多维几何参数的联合分布的难题,亟待提出一种能够灵活且准确地对实测裂隙的多参数联合分布进行概率密度估计与采样的方法,从而实现DFN 的多参数模拟。
深度生成模型属于一种深度学习模型[12-13],其优势在于能够学习分布类型未知的高维联合分布并从中采集高质量的样本,能够克服传统统计学模型难以扩展到高维问题的不足[14-15],对于突破DFN多参数模拟的瓶颈具有较大的潜力。深度生成模型近几年开始被应用于建立更加真实的大尺度地质构造三维模型[16],但尚未被引入DFN 建模的研究中[17-18]。
2017年,Papamakarios 等[19]与Kingma 等[20]提出了一种新的深度生成模型——自回归流(Autore⁃gressive Flow),该模型通过建立易解的概率密度(Tractable Density)实现对于复杂分布下对数似然函数值的精确计算[21],克服了其他基于变分推断(Variational Inference)的深度生成模型需要对概率密度进行近似估计的不足[12],具备能够实现更加准确的概率密度极大似然估计的优势[14-15],因而成为了目前深度生成模型领域的研究热点,应用于概率密度估计[19]、变分推断[20]、图像生成[22]、语音合成[23]、文本生成[24]等方向的研究。本文将自回归流模型引入DFN 建模中。裂隙网络的几何参数通常具备优势分组的现象,即岩体在多次构造作用下产生的裂隙网络的几何参数聚集于几个峰值附近[6,8],导致其几何参数的分布呈现出多峰的特点。然而,自回归流模型的初始分布通常采用一个单峰的高斯分布,对于多峰分布的估计能力有待提高。因此,本文提出基于改进自回归流模型的裂隙多参数模拟方法,将自回归流模型的标准化特征空间的高斯分布改进为高斯混合分布并结合DensityPeak 聚类算法[25]提出了密度峰值聚类自回归流(Density Peak Clustering Autoregressive Flow,DPCAF)模型。其中,密度峰值聚类(Density Peak Clustering)算法于2014年发表于Science[25],是目前最受关注的聚类算法之一,具有能够从任意维度任意形状的数据中快速确定簇的数量与聚类中心的优势[26],适用于裂隙几何参数的聚类问题。本文提出DPCAF 模型以期能够有效拟合裂隙几何参数的多维多峰联合分布,有效提高裂隙网络多参数模拟的精度,并使得DFN 模型更加真实地反映岩体内部的裂隙分布。
2 研究框架
提出的基于密度峰值聚类自回归流(Density Peak Clustering Autoregressive Flow,DPCAF)模型的三维裂隙网络建模方法的研究框架如图1所示,具体如下:
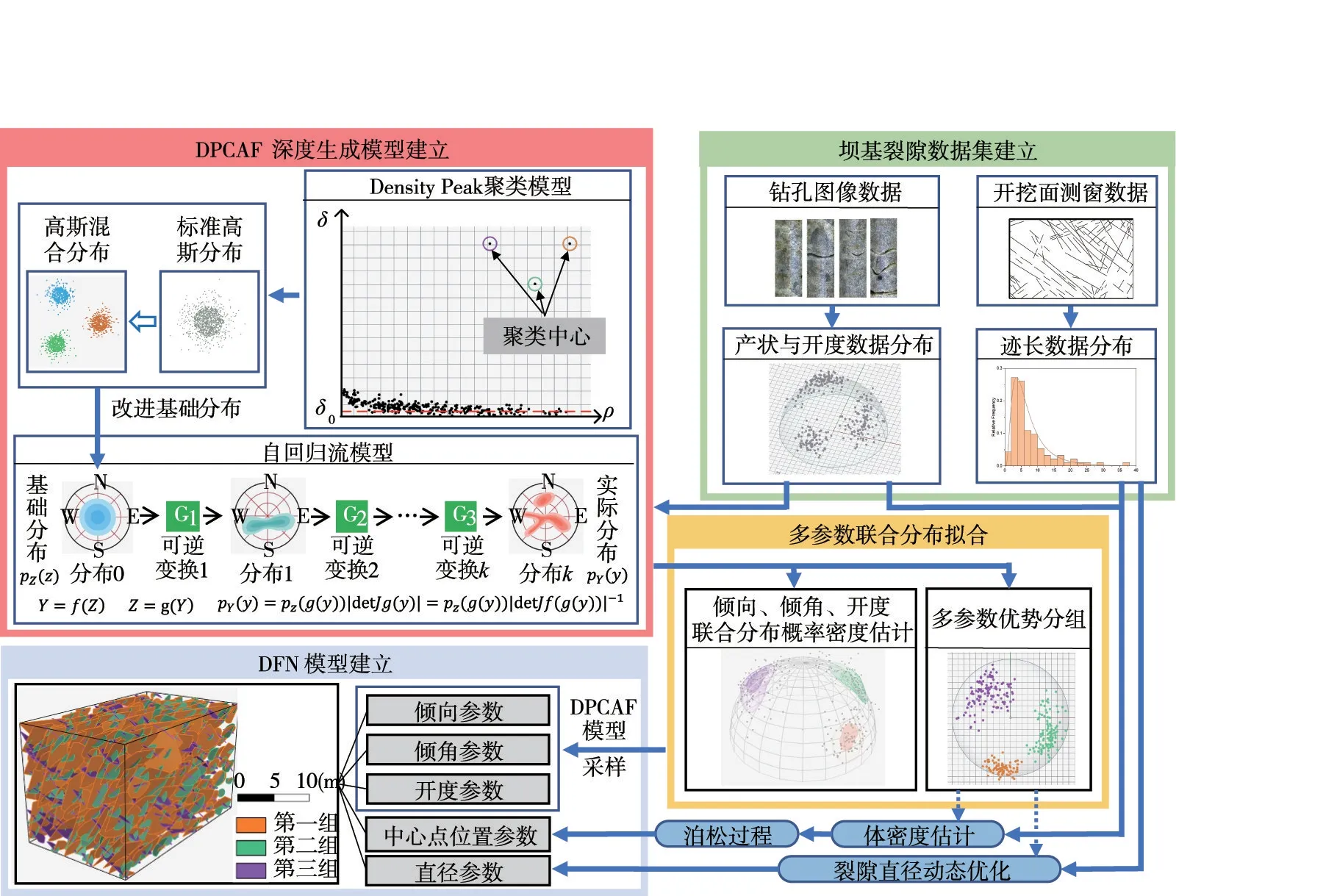
图1 研究框架
(1)建立坝基裂隙数据集。从坝基裂隙岩体的钻孔图像数据中提取出岩体内部裂隙的倾向、倾角、开度三个维度的几何信息[6,27-28],由于钻孔图像中未包含裂隙直径信息,从建基面测窗数据中统计裂隙迹长的分布,用于辅助推断裂隙直径参数;
(2)建立DPCAF 深度生成模型。将自回归流模型标准化特征空间的基础分布由标准高斯分布改进为高斯混合分布,并结合DensityPeak 聚类算法确定裂隙分组数量与聚类中心,建立改进的自回归流模型DPCAF,利用产状与开度的实测数据集训练DPCAF 模型参数;
(3)多参数联合分布拟合。利用训练完成的DPCAF 模型对倾向、倾角、开度参数的联合分布进行概率密度估计,同时实现多参数优势分组;
(4)DFN 模型建立。基于裂隙多参数优势分组结果,联合测窗数据与钻孔图像数据对每组裂隙的体密度(单位体积内的裂隙数量)进行估计,并通过泊松过程得到各组裂隙中每一个裂隙面的中心点坐标参数;利用DPCAF 模型对倾向、倾角、开度参数随机采样;基于测窗数据中的裂隙迹长分布优化裂隙直径参数;最后,基于圆盘裂隙模型,建立三维离散裂隙网络。
3 基于密度峰值聚类自回归流的DFN 多参数模拟方法
3.1 密度峰值聚类自回归流模型由于裂隙网络的几何参数普遍存在优势分组的现象,其分布呈现出多峰的特点。然而,自回归流模型的初始分布采用一个单峰的高斯分布,估计多峰的概率密度的能力有待提高。针对以上不足,本文提出的DPCAF 模型,将自回归流模型的标准化空间的高斯分布改进为一个由均值、方差和各分支的混合比例所参数化的高斯混合分布,并结合DensityPeak 算法,以无监督的形式实现裂隙多参数优势分组与多参数联合概率密度估计的多任务学习,提高对实测裂隙数据多峰分布的拟合精度。
自回归流模型属于一种标准化流(Normalizing Flow)[14-15],如图2所示,其核心思想是将一系列简单的可逆变换函数作为组件以“流”的形式依次嵌套为一个可逆的复合函数,构造出一个具有更强拟合能力的非线性双射,通过在实际数据的目标分布与已知的基础分布之间互相转换实现多维联合分布的估计。
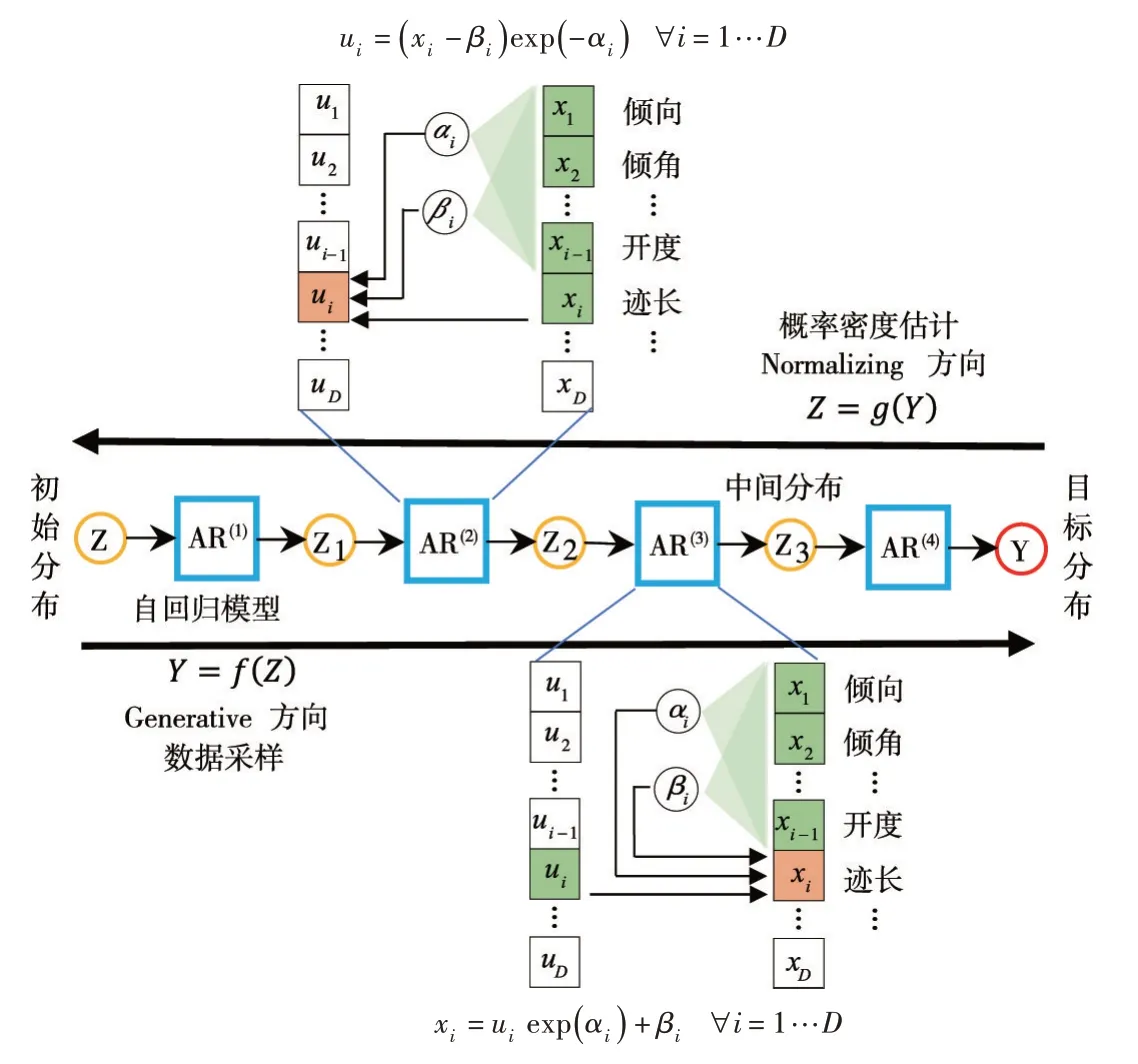
图2 自回归流模型网络结构[19]
令随机变量Z ∈RD服从已知的基础分布,随机变量服从目标分布。利用N 个双射函数 f1,f2,…,fN的复合函数f 构建可逆变换,将基础分布变换为一个未知的目标分布,即,其逆变换为双射函数 g1,g2,…,gN的复合函数g,即。 根据Change-of-Variables 公式[14],令J 为雅克比行列式算子,则目标分布的概率密度函数如下:
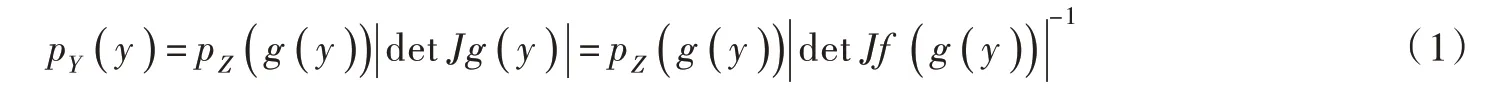
变换f 的方向称作生成方向(Generative Direction),是进行采样时的数据流向,逆变换g 的方向称作标准化方向(Normalizing Direction),通常将复杂不规则的目标分布变换为多元标准高斯分布[19-20],是评估模型概率密度值的数据流向,如图2所示。为了保证模型训练和预测的计算效率,要求可逆变换f 具有易解的雅克比行列式(Tractable Jacobian Determinant)。因此,引入另一种深度生成模型——自回归模型(Auto-Regressive Model,AR)[29],该模型基于概率链式法则将联合概率密度分解为每一个维数上的条件概率的乘积[29],并逐个对每一维数据的条件概率分布进行“自回归”计算。以自回归模型作为双射函数 fi的标准化流模型称作自回归流模型(Autoregressive Flow)[19-20],其中双射函数 fi具有如下的自回归形式:

式中:τ称作变换函数(transformer)[14];ci称作第i 个调节函数(conditioner);。
该公式的自回归特性体现在:第i 个调节函数ci只能以第1 个至第i-1 个维度的变量z1:i-1为输入,其雅克比矩阵为下三角阵。将公式(2)作为Normalizing 方向的逆变换g[19],并选择仿射变换形式的变换函数τ[14],如下:
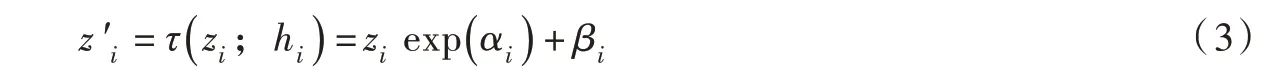
式(3)中的变换函数τ是可逆的,且形式简洁且引入的参数量较少,在实测裂隙数据的小样本数据集上不易过拟合[19-20],同时对于裂隙数据具备足够的拟合能力。此时雅克比行列式的绝对值为:

用掩模自编码器(Masked AutoEncoder for Density Estimation,MADE)[29]构建调节函数ci,对多参数之间的相关性进行建模,逐个计算每个参数的条件概率并依据链式法则求得联合概率密度。在训练自回归流模型的过程中,直接将负对数似然函数作为损失函数,通过梯度下降对每一个双射函数 fi内部的仿射变换参数与掩模自编码器参数进行优化。
本文提出的DPCAF 模型中,基于高斯混合分布与密度峰值聚类改进自回归流模型的方法如下:
首先,建立混合高斯分布作为DPCAF 模型的基础分布。高斯混合分布是一种混合分布,记作:

式中:Gi为混合分支,服从高斯分布;为支密度;为混合比例。
利用DensityPeak 算法搜索密度峰值点作为聚类中心,将簇的数量作为高斯混合分布中分量的数量,定义DPCAF 模型的基础分布,其中每一个分量对应裂隙网络的一个优势分组。将深度生成模型的先验分布由单峰分布改进为混合分布是提高模型对于多峰分布拟合能力的有效手段[30-32]。以赤平极射投影图上的裂隙产状数据为例,对比自回归流模型与DPCAF 模型的基础分布,如图3所示。
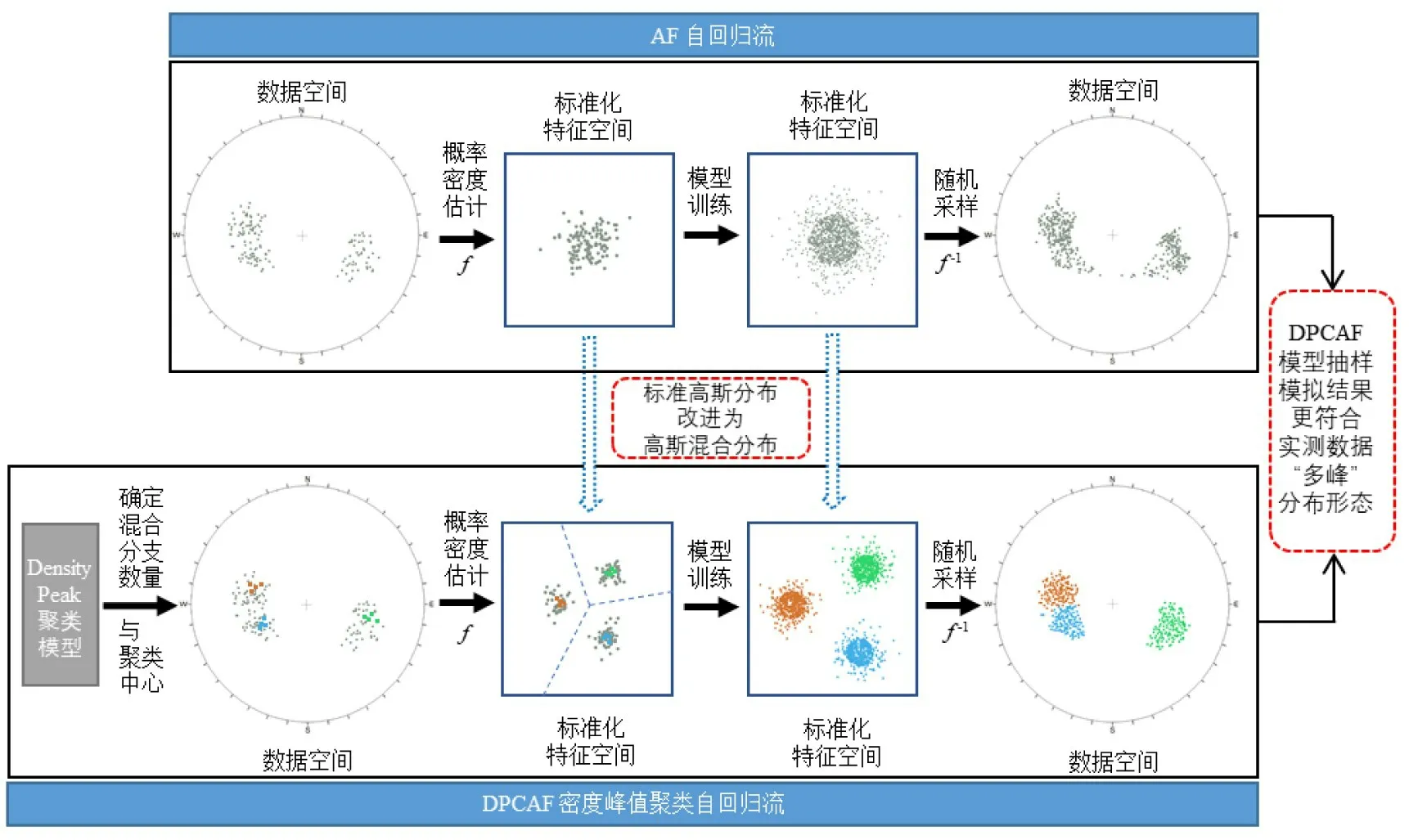
图3 DPCAF 模型改进自回归流模型示意
DensityPeak 算法所定义的密度峰值点包含两方面特征[25]:(1)该点的局部密度大于其邻近数据点;(2)该点与比它密度更高的数据点之间的距离较远。

式中:ρi为局部密度,1/mm3;dc为截断距离,mm;dij为数据点i 至数据点j 的距离,mm。当a<0时当a ≥0 时。

式中δi为与密度更高点的距离,mm。
其次,在以局部密度ρi为横坐标,以距离δi为纵坐标,绘制出DensityPeak 决策图上,自动提取出聚类中心附近的少量样本点,作为已知分组标签的训练数据。搜索标签数据的规则如下:(1)样本点按照其在决策图上的局部密度从大到小的顺序筛选;(2)样本点与具有更高密度的最近点的距离大于设定的δ0距离阈值,mm。
最后,利用分布拟合空间的实测数据与DensityPeak 算法提取的部分数据标签训练DPCAF 模型。将自回归流的基础分布定义为:

式中:高斯混合分布的混合分支数量为M,其中第k 个是均值为μk标准差为σk的高斯分布。
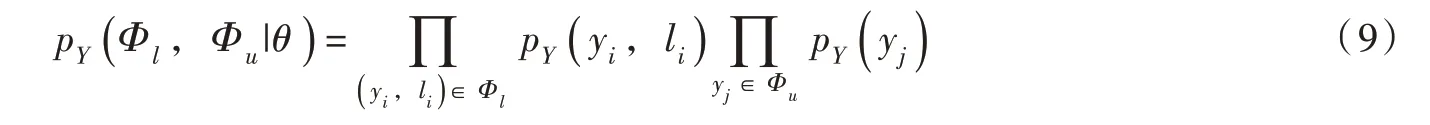
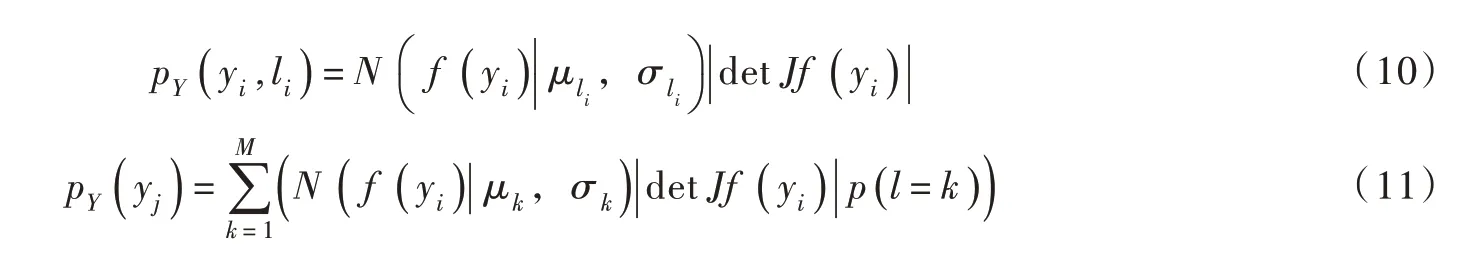
在最大似然估计的过程中对式(9)中的联合似然函数进行最大化。根据贝叶斯定理,利用上述概率密度估计的结果计算出已知样本点x 条件下标签l 的条件分布,并训练贝叶斯分类器实现裂隙分组。
3.2 基于DPCAF 模型的坝基岩体裂隙网络多参数模拟流程为了更好地揭示钻孔图像数据中倾角、倾向、开度三个裂隙几何参数的分布,本文建立了一个可逆的球坐标系转换,将实测数据点映射到分布拟合空间的点,如图4所示。其中:α 为裂隙面倾向,(°);β 为裂隙面倾角,(°);δ 为裂隙开度,又称作隙宽,mm;x,y,z 为分布拟合空间中的直角坐标系下的坐标。其中对于裂隙开度这一维度,本文使用数据点到球坐标中心点的径向距离对其进行表征,建立球面半径与开度的转换关系为,单位统一采用mm,其中δ0为开度的平均水平,实际工程的裂隙开度一般位于毫米至厘米量级,因此取δ0为10 mm,R0是开度等于δ0时的球面半径,其数值也取为10 mm,λ 为缩放系数,本文取为0.1。
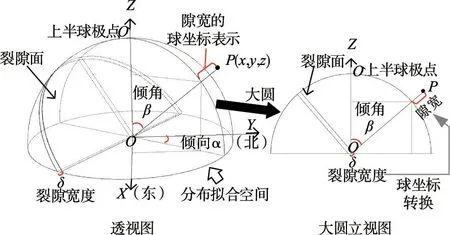
图4 裂隙倾向、倾角、开度参数的球坐标系转换过程
DFN 多参数模拟的具体步骤如下:
(1)将倾角、倾向、开度的原始实测数据通过上述球坐标系转换为分布拟合空间的数据,并对DPCAF 模型进行训练,将DPCAF 模型输出的分布拟合空间每个数据点的标签映射回原始数据,得到三个参数的优势分组结果;
(2)DPCAF 模型输出分布拟合空间的联合概率密度函数,对从中采集的样本进行球坐标系转换的逆变换,从而得到倾角、倾向、开度参数的随机模拟结果;
(3)基于裂隙网络参数化建模计算模拟迹长分布下实测迹长数据平均对数似然,以裂隙直径Gam⁃ma 分布的形状参数和逆尺度参数为控制变量,以最大化似然函数为优化目标,利用粒子群优化(Par⁃ticle Swarm Optimization,PSO)算法[33]进行求解,从而得到直径参数的随机模拟结果。
4 工程实例
以我国西南某水电工程的坝基岩体为研究对象,基于所提出的基于DPCAF 模型的DFN 多参数模拟方法,针对河床高程范围内的建基面下方50m×30m×30m(长×宽×深)区域范围内的裂隙网络进行三维建模。钻孔图像数据包含309 条实测裂隙,开挖面测窗数据包含231 条实测裂隙,如图5所示。

图5 坝基岩体裂隙数据
4.1 基于DPCAF 模型的坝基DFN 多参数模拟从钻孔图像中提取的倾向、倾角与开度实测数据通过球坐标系转换至分布拟合空间的结果如图6所示,图中黑色的点代表转换后得到的数据,半透明的半球面是开度等于10 mm 的等参面。
首先,利用DensityPeak 聚类算法确定聚类的分组数量,以及每一组的聚类中心。可以明显地发现DensityPeak 决策图的右上角出现三个聚类中心点,而其余点均分布于靠近横轴的区域,因此优势分组数量为3 组。将决策图中的点映射回三维坐标系内可以定位三个聚类中心的位置,如图6所示。在DensityPeak 决策图上自动搜索聚类中心附近的标签数据,设定标签数据在决策图中纵坐标的阈值为图6 中的红色虚线,最终得到的每一组的标签数据为20 个。

图6 DensityPeak 算法搜索聚类中心
其次,利用所有实测数据点以及DensityPeak算法自动搜索得到的标签信息对DPCAF 模型进行训练。图7 对训练完成的DPCAF 模型从分布拟合空间的数据中学习的三维联合概率密度的形状进行了可视化,其中对于每组裂隙绘制了两个半透明的等概率密度曲面。
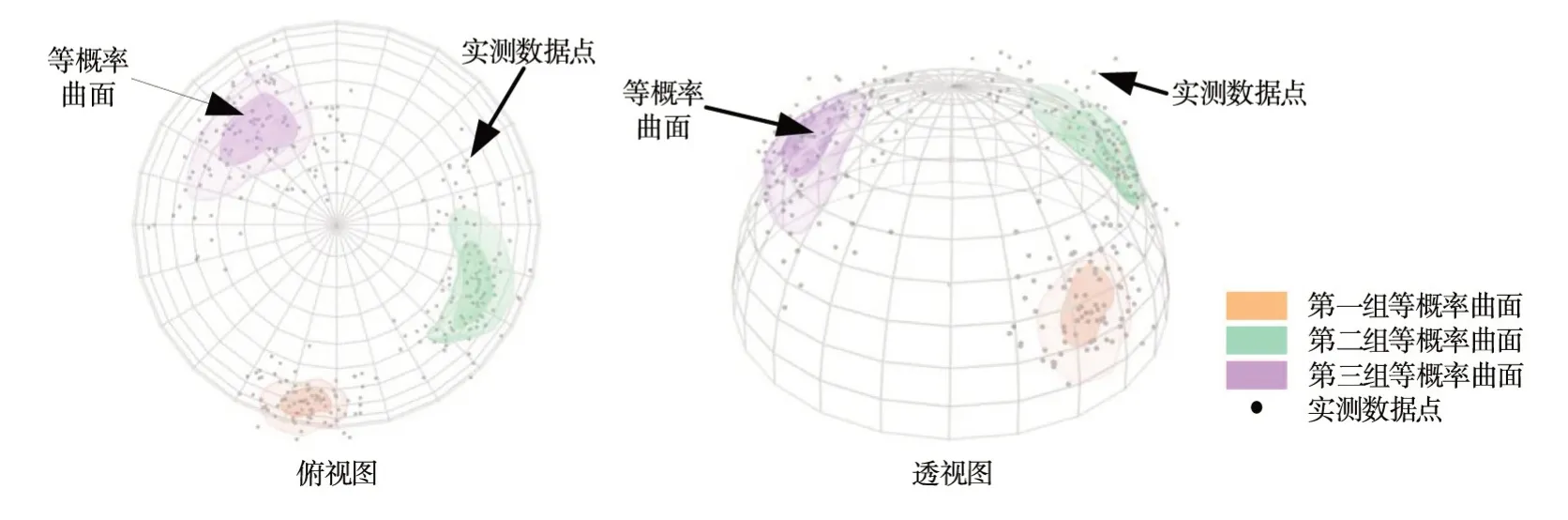
图7 三维联合分布概率密度估计结果
再者,结合钻孔图像与开挖面测窗中的裂隙数据,通过体密度估计得到三组裂隙网络中裂隙数量分别为530、460 与470,并采用泊松过程对圆盘裂隙的中心点位置进行随机模拟。经过拟合优度检验,三组裂隙的实测迹长都服从对数正态分布。假设圆盘裂隙直径服从Gamma 分布,通过动态优化得到第一组的形状参数为3.804,逆尺度参数为0.827,第二组的形状参数为3.075,逆尺度参数为1.235,第三组的形状参数为4.982,逆尺度参数为1.400。
根据所建立的概率分布可以生成多个三维离散裂隙网络,对其中一次随机模拟生成的范例进行可视化如图8所示。进一步对该裂隙网络的迹线模拟结果进行数值检验,采用单尾F 检验与双尾t 检验,显著度设置为0.05,如表1所示。F 检验与t 检验的P 值均大于显著度,说明模拟迹长的方差和均值都与实测结果无显著差异。提出的DFN 建模方法基于深度生成模型充分挖掘了坝基裂隙岩体内部钻孔与开挖面测窗数据所蕴含的裂隙几何信息,多元数据互相印证,提高了DFN 模型的可靠性,为水电工程坝基裂隙岩体的工程地质分析与决策提供了重要支撑。
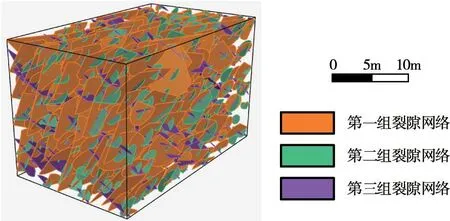
图8 坝基三维离散裂隙网络随机模拟范例

表1 迹线随机模拟范例数值检验
4.2 对比分析与讨论首先,通过DPCAF 多参数模拟与传统单参数模拟结果的对比分析,以及基于典型分布假设方法与DPCAF 方法的倾向与倾角二参数联合分布估计的对比分析,验证DPCAF 模型的准确性;其次,为了验证DPCAF 模型对于多维参数联合分布估计的有效性,对基于GMM 模型与DP⁃CAF 模型的倾向、倾角、开度多参数模拟结果进行对比分析与讨论。
4.2.1 裂隙迹线数据参数相关性的单参数模拟与DPCAF 模拟对比分析 本案例采用Mendoza-Torres等[10]的文章中给出的裂隙迹线数据进行对比分析,如图9(a)所示,该裂隙网络为一组由张拉裂隙与剪切裂隙构成的共轭裂隙系统,包含两组裂隙,其中一组优势裂隙沿南北方向延伸,具备较大的迹长但裂隙数量较少,另一组裂隙沿东西方向延伸,迹长相对较小但裂隙数量较多,因此,该裂隙系统的走向与迹长具备特定的依赖关系[10],如图9(a)所示,其中迹长为前10%的裂隙迹线标记为黑色,其余裂隙迹线标记为蓝色。迹长与走向分别进行单参数随机模拟生成的一个范例如图9(b)所示,采用DPCAF 模型对迹长与走向进行多参数随机模拟生成的一个范例如图9(c)所示。显然,实测数据中迹长较大的裂隙主要集中于南北走向,然而,采用传统的单参数方法模拟的大迹长裂隙没有呈现出明显的优势走向,甚至有更多的大迹长裂隙为东西走向。因此,单参数模拟方法丢失了裂隙迹长与走向之间的依赖关系。相反,图9(c)中的模拟结果与图9(a)具备良好的一致性,因此DPCAF 模型在进行裂隙几何参数联合分布估计的过程中能够良好地捕捉迹长与走向之间的依赖关系。
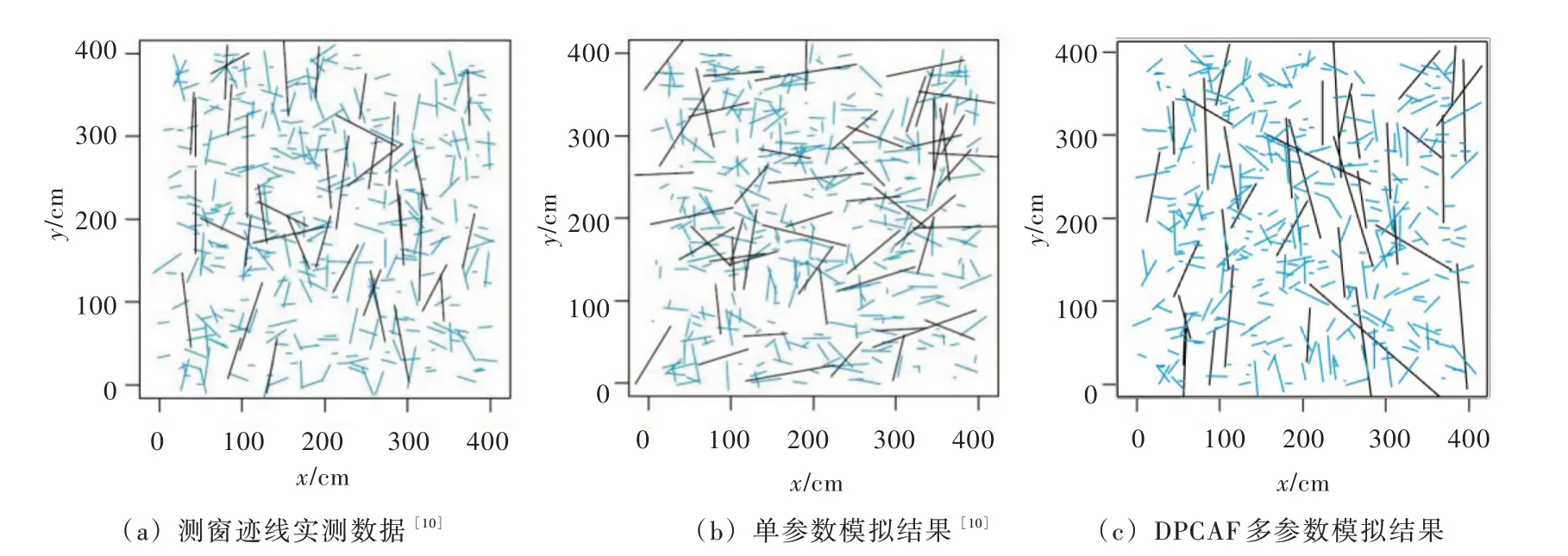
图9 2D 裂隙网络随机模拟范例对比
为了将走向与迹长之间的关联结构进行可视化,将图9 中裂隙的几何参数绘制于图10(a)—(c)的散点图中,并进一步利用Mendoza-Torres 等[10]的研究中所采用的方法,将散点图转换为分位数分布图,如图10(d)—(f)所示。分位数分布图展示的是分位数的概率,例如,对于散点图中横坐标所表示的裂隙走向处于中位数的点在分位数分布图中的横坐标u=0.5,而散点图中横坐标处于四分位数的点在分位数分布图中的横坐标u=0.25,对于纵坐标的转换方法同理。实测数据中两个变量的秩相关系数为0.635,说明走向数据与迹长数据不是独立的[10]。分位数分布图10(d)与图10(f)中的点都呈现出相同的分布规律,然而图10(e)中的点趋向于离散的均匀分布,因此DPCAF 多参数模拟的结果有效地还原了走向与迹长两个变量之间的二元结构,能够克服传统单参数方法难以模拟裂隙参数之间关联关系的不足。

图10 裂隙走向与迹长随机模拟范例的散点图与分位数分布图对比
4.2.2 裂隙产状数据二参数联合分布的典型分布模拟与DPCAF 模拟对比分析 目前离散裂隙网络模拟方法中,涉及到联合分布估计的参数只有倾向和倾角参数,通常假设倾向与倾角服从双正态分布或Fisher 分布。Shanley-Mahtab 数据集[34]为Shanley 与Mahtab 从美国亚利桑那州San Manual 铜矿收集的286 个裂隙产状测量值。该数据集被广泛地应用于关于产状分布的研究中[11]。因此,本文将所提出的DPCAF 模型应用于Shanley-Mahtab 数据集中第一组与第二组产状数据的分布估计,并与传统方法进行对比,结果如表2所示。Fisher 分布的估计精度大于双正态分布,但两者的对数似然函数都小于0,而DPCAF 模型对两组产状数据分布估计的对数似然函数都在8 以上。可见,实测产状数据的分布可能并不完全服从双正态分布与Fisher 分布的假设,而DPCAF 模型的概率密度估计结果更加接近数据的实际分布。

表2 产状数据概率密度估计精度对比
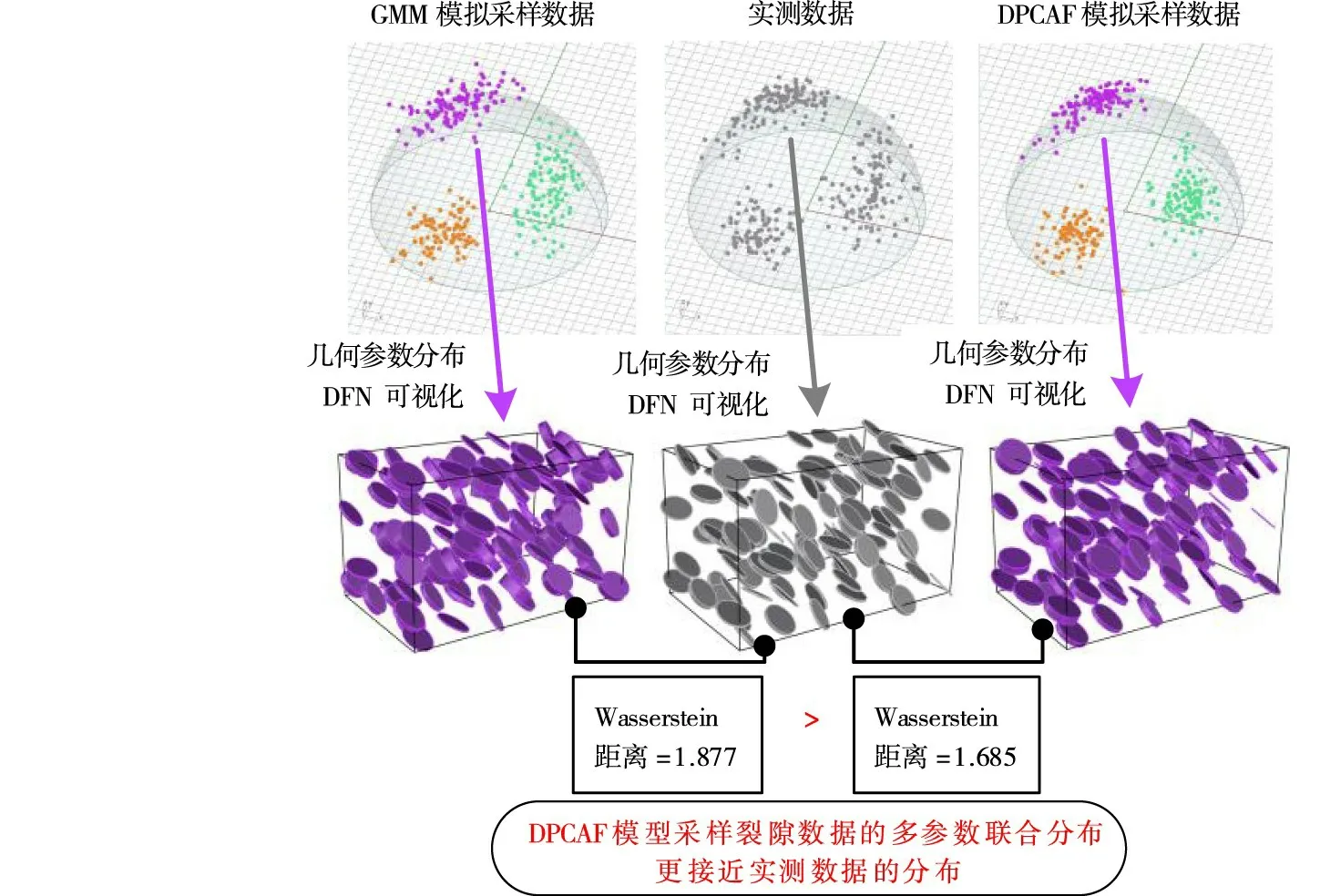
图12 采样模拟裂隙数据范例可视化对比
4.2.3 钻孔图像数据多参数联合分布的GMM 模拟与DPCAF 模拟对比分析 为了对倾向、倾角与开度数据的概率密度估计的精度进行评价,将提出的DPCAF 模型与目前主流的有限混合模型(Finite Mixture Model)——高斯混合模型(Gaussian Mixture Model,GMM)进行对比,如图11所示。
三维的GMM 模型的每一个分支对应的等概率密度曲面都为“置信椭球”,但由于实测裂隙开度参数的分布较为集中,对应于球坐标系下的三维空间点基本分布于开度等参球面附近,而不是呈椭球状分布。GMM 用“置信椭球”拟合实际数据时表现出了一些系统性的偏倚,例如,图11(b)中绿色的第二组和图11(c)中紫色的第三组裂隙所估计的置信椭球的一端明显向开度等参球面外侧翘起。相反,DPCAF 模型可以建立任意复杂不规则形状的分布,所估计的概率密度形状良好地拟合了真实数据点的分布。采用评价概率密度估计的精度的常用评价指标——平均对数似然(Mean Log-Likelihood)[19]进行量化对比。其中,DPCAF 模型的平均对数似然都在21 至22左右,而GMM 模型的平均对数似然都在-6 以下,可见DPCAF 的概率密度估计精度高于GMM。
进一步对比分析GMM 与DPCAF 模型的采样模拟的误差,控制采集样本的数量相同,采用模拟数据分布与实测数据分布之间的Wasserstein 距离[35]作为模拟误差的评价指标,如表3所示。

表3 采样模拟裂隙数据范例误差对比
图12 以第三组裂隙为例,分别采用球坐标可视化与DFN 可视化方法对三维数据分布建立形象直观的表达。在DFN 可视化方法中,固定每个圆盘结构面的中心点位置和半径,将采样数据所包含的倾向、倾角和开度几何参数分别赋值给不同的圆盘模型,得到虚拟的离散网络模型,其中为了提升可视化效果将开度数据乘以500 作为圆盘的厚度,如图12所示。可以发现,DPCAF 采样的每一组裂隙的分布以及三维裂隙的整体分布都比GMM 的采样结果更加接近实测数据,从而证明了本文提出的DPCAF 模型的模拟精度更高。
5 结论
裂隙几何参数分布的估计与拟合是三维离散裂隙网络随机模拟的核心环节。然而,现有的DFN建模方法基于Gamma 分布、对数正态分布、Fisher 分布等典型分布对单参数的边缘分布或倾向倾角的联合分布进行估计,面临着无法拓展到更多维裂隙参数的复杂联合分布的难题。针对上述问题,本文提出了基于改进自回归流模型的DFN 多参数模拟方法,取得了如下成果:
(1)考虑裂隙几何参数具有优势分组的特点改进自回归流模型,将标准化特征空间的高斯分布改进为高斯混合分布,并结合DensityPeak 算法搜索聚类中心,提出了DPCAF(Density Peak Clustering Autoregressive Flow)模型,克服了自回归流模型对于裂隙数据多峰分布拟合能力的不足;
(2)将自回归流模型中基于可逆变换拟合复杂多维联合分布的思想引入DFN 建模中,有效解决了DFN 多参数模拟所面临的多维联合分布的概率密度估计与采样的核心难题,在DFN 建模的过程中同时完成多参数优势分组与多参数概率密度估计;
(3)工程应用表明,对于实测裂隙数据的复杂联合分布,本文提出的DPCAF 模型相比与传统基于典型分布的估计方法具备更强的拟合能力,并且能够有效还原多参数之间的关联关系;DPCAF 模型相比于双正态分布与Fisher 分布对于产状数据的概率密度估计精度更高,相比于GMM 模型对于钻孔图像中的倾向、倾角、开度数据联合分布的概率密度估计的平均精度更高,且采样结果的误差缩小了7.84%。因此,DPCAF 模型能够有效提高多参数拟合的准确性,保证DFN 建模的精度。
本文提出的改进自回归流模型能够为工程分析过程中涉及到的多维联合概率密度估计问题提供一种新的技术手段[36-37]。此外,随着水电工程地质勘测与感知技术的不断进步[38],未来将可能获取更多种类的裂隙数据,可以将其引入DFN 多参数模拟中进一步提升裂隙网络模型的可靠性。

