冰期河湖与大气的热交换模型
杨开林
(流域水循环模拟与调控国家重点实验室,中国水利水电科学研究院,北京 100038)
1 研究背景
河湖与大气的热交换模型是计算分析冰凌形成、发展、消融时空变化规律的基础,也是太阳能利用、气候变化、水文、水资源研究的重要课题。河湖热交换是指敞露水面、冰盖和雪盖与太阳辐射、长波辐射、表面蒸发和对流、降雪或降雨之间的热交换。
Ashton[1]归纳总结了当时河湖与大气的热交换模型,建议采用Angström日照百分率模型和Wun⁃derlich 云量百分率模型计算太阳辐射,并在分析冰情的过程中采用线性化模型描述冰期河湖与大气的热交换,即取河湖与大气的净热通量ϕn=-hsa(Ts-Ta),式中:hsa为热交换系数,Ts为河湖表面温度,Ts为气温。不过,他没有给出如何选取hsa的方法。
Angström 和Wunderlich 模型的特点是采用晴天直射为云天太阳辐射计算的起始值,没有考虑晴天散射辐射的影响。王炳忠等[2-3]以理想大气晴天日射为云天太阳辐射计算的起始值,考虑了晴天散射辐射的影响,成果被《凌汛计算规范(SL428—2008)》采用,不过计算的过程比较复杂,需要查专用图表。和清华等[4]利用中国54 个站1961—2000年的逐日太阳总辐射和日照百分率资料,以线性日照百分率模型为基础,分别以天文辐射、晴天日射和理想大气日射作为起始值建立了各站的太阳辐射回归方程,推荐采用以天文辐射为起始值计算云天辐射。这就产生了一个问题,在河湖冰工程中采用那一个太阳辐射模型较好。
Ashton 提出的线性化模型形式已经在冰工程中得到广泛应用[5-8]。沈洪道[6]针对北美地区,采用hsa=20.0W/(m2·℃)。蔡琳等[7]和冀鸿兰等[8]针对黄河,当水面敞露时,取hsa=10.0W/(m2·℃);当冰封时,取hsa=1.5 W/(m2·℃)。显然,从上述中会发现一个问题,hsa的取值相差相当悬殊,解决这个问题的关键有两个,一是河湖与大气热交换模型的选取;二是热交换模型的更加合理的线性化方法。
本文的主要目的是,基于太阳能利用、气候学、水文和水资源等学科的研究成果,建立适用于冰封河湖与大气的非线性热交换模型,然后利用历史天气资料,以及笔者团队进行的太阳辐射、水温、冰温、雪温、气温和风速的原型观测,探索对长波辐射、蒸发和对流热交换模型的更加合理的线性化方法,以揭示和发现一些重要的普遍性规律。
2 太阳辐射模型
气候学计算云天太阳辐射的日照百分率模型是由Angström(1924)提出的[1],数学描述是:
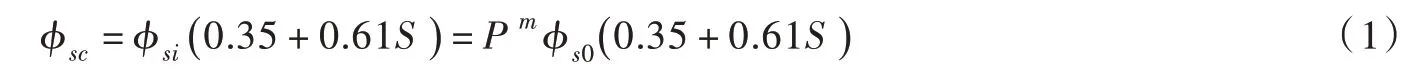
式中:ϕsc为云天的日射热通量,W/m2;ϕsi=Pmϕs0为晴天直射热通量,W/m2;ϕs0为天文辐射热通量,W/m2;P 为所有波长范围内的大气平均透明系数;m 为光学大气质量;S 为日照百分率,表示实际日照时间Treal与理论日照时间Tsun的比值,即,有0 ≤S ≤1.0。
天文辐射ϕs0是指完全由地球天文位置决定的到达地球大气顶界的太阳辐射,与日地距离的平方成反比,随太阳高度角的增加而增加[9]。
和清华等[4]推荐采用以天文辐射为起始值计算云天辐射:

采用上式全国54 个站的相对误差变化在3.33%~18.75%之间,平均为8.39%。
2.1 云量百分率模型在我国设有日照观测站的地区很少,用云量百分率代替日照百分率已成为计算云天太阳辐射的首选因子,因为云量是气象站的常规预报项目。
基于Angström日照百分率模型,Wunderlich 提出的云量百分率模型[1]是:

式中:C 为云量,%,0 ≤C ≤100%。
基于和清华等的日照百分率模型,当取S=1-C2,由式(2)得下述云量百分率模型:

由于Wunderlich 云量百分率和Angström日照百分率模型一样,都是以晴天直射作为云天辐射的起始值,没有考虑晴天散射辐射的影响。
当考虑晴天散射的影响时,晴天散射可按Berlage 公式(1928)计算[2]:

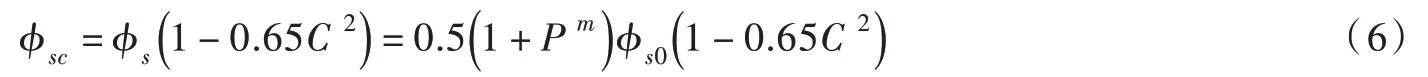
2.2 大气平均透明系数P 和光学大气质量m 的计算王炳忠等[3]研究了我国大气平均透明系数P 和光学大气质量m 的计算,不过过程比较复杂,Pm的计算需要查专用图表。鉴于此,本文将采用Glover和McCulloch 的方法计算Pm[1]:

需要指出的是式(7)只有在Pm>0 才有意义。根据Klein 的研究,m 可用下式计算:
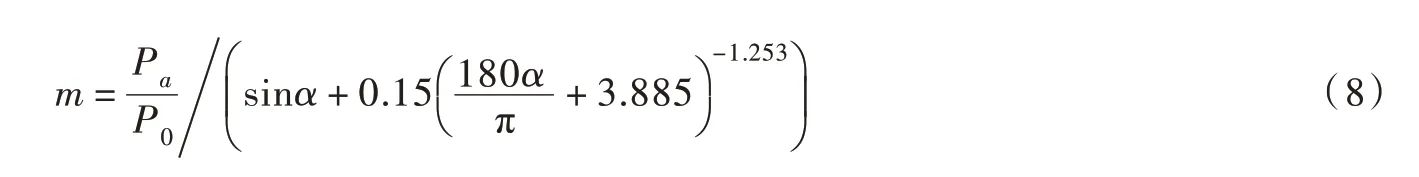
式中:Pa为观测地的大气压,hPa;P0为海平面大气压,hPa,一般取1013.25 hPa。
2.3 模型的比较在2016年1—4月期间,笔者团队在黑龙江省漠河市北极村黑龙江边开展了太阳辐射的实测,下面将以此为依据比较上面的3 个云量百分率模型:以晴天直射为起始值的Wunderlich 式(3);以天文辐射为起始值的和清华和谢云式(4);本文晴天日射为起始值的式(6)。
图1(a)示出了2016年4月白天平均云量随日期的变化(资料来源https://tianqi.911cha.com /mohe/2016 -4.html,以下历史气象资料来源相同),其中:n=92 表示2016年4月1日;云量C=1.0 是天降大雪的完全阴天;云量C<0.6 可视为晴天。图1(b)(c)(d)分别示出了式(3)(4)(6)计算的2016年4月份太阳辐射的辐照度与实测值的比较,其中天文辐射ϕs0的计算可参考文献[9]。
根据图1,可得重要结论如下:
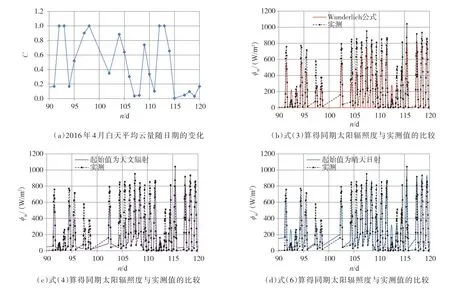
图1 黑龙江省漠河市北极村黑龙江边实测太阳辐射与理论计算比较
(1)式(6)计算太阳辐射结果与实测值吻合最好,式(3)和式(4)次之,例如,当n=115 时,C=0 为完全晴天,实测最大ϕsc=1042.1 W/m2,而式(3)(4)(6)计算的最大ϕsc值分别为814.6、811.5、932.1 W/m2。这表明所提出的式(6)用于计算晴天日射的模型及大气平均透明系数和光学大气质量的方法是比较符合实际的。
(2)当白天平均云量C≥0.6,太阳辐射理论计算值与实测值均偏差较大,特别是连续2 天C=1.0的降雪阴天。原因可能是:①白昼日平均云量资料来源于气象站观测资料,与观测点存在一定偏差;②白昼不同时间的云量相差较大。改进的途径是用白天分时段平均云量代替白天平均云量。
3 长波辐射模型
河湖长波辐射包括水体或者冰盖和雪盖表面的长波辐射与大气长波逆辐射。
3.1 河湖的长波辐射河湖作为一个近乎黑体,长波辐射的热通量可由斯蒂弗-博尔茨曼四次方定律[1]计算:

式中:ϕb为河湖长波辐射的热通量,W/m2;σ=5.67×10-8W/(m2·K4)为斯特凡·玻尔兹曼常数;εw为修正系数,对水、冰和雪可取εw=0.97;Ts为河湖表面温度,℃,对敞露水面指水面温度,冰封时指冰盖表面温度,有雪盖时指雪面温度。在水面温度Ts=0℃时,ϕb=306 W/m2。
3.2 大气长波逆辐射大气长波逆辐射也可按斯蒂弗-博尔茨曼(Stefan-Boltzmann)定律[1]计算:
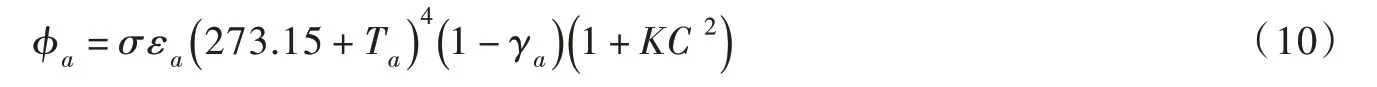
式中:ϕa为长波大气逆辐射到河面的热通量,W/m2;Ta为河面上1.5 m 高测得的气温,℃;εa为晴天的大气发射率;γa为河湖表面对大气长波逆辐射的反射率,γa≈0.03;K 为系数。Wunderlich 根据美国Tennessee 地区观测资料,取K=0.17[1]。
对于晴天的大气发射率εa,我国常常采用Idso-Jackson公式,εa只是气温Ta的函数[10],而Ashton[1]推荐采用Brant 公式,其εa只是水汽压ez的函数。黄妙芬等[11]利用实测资料比较研究了国际上常用的10 个计算εa的经验公式,包括Angström 公式、Brant 公式、Idso-Jackson 公式和Iziomon 公式等,结果表明:Iziomon 公式具有最小的平均绝对误差和均方差,具有最大的一致性指数IA 和线性相关系数LCC;Brant 公式次之;Idso-Jackson 公式具有最大的平均绝对误差和均方差,以及最小的一致性指数IA 和线性相关系数LCC,因此,推荐采用Iziomon 公式:
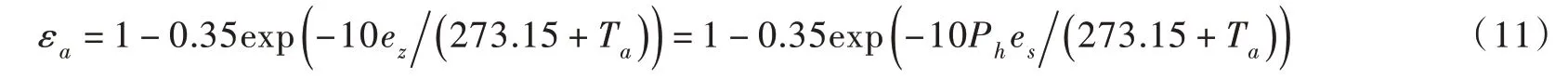
式中:ez=Rhes为离河面高度z=1.5 m 处的空气中水汽压,hPa;es为空气的饱和水汽压,hPa;Rh为空气的相对湿度。当空气湿度饱和时,Rh=1.0。
由式(11)可知,εa不仅与气温Ta有关,而且与水汽压εz或相对湿度Rh和饱和水汽压es有关。本文在下面的分析中,也采用Iziomon 公式计算晴天的大气发射率εa。
饱和水汽压es是随表面温度Ts的升高而增加,随Ts的降低而减小,世界气象组织(WMO)1996年推荐采用马格纳斯-蒂托斯(Magnus-Tetons)公式计算[12]:

式中:Ts为河湖表面温度,℃;es0≈6.11 hPa 为Ts=0 ℃时的饱和水汽压;a 和b 为常数,对水面:Ts>0 ,a=17.62,b=35.86;对冰面:Ts≤0,a=21.88,b=7.66。
4 蒸发和对流模型
水面蒸发量模型的研究已有200 多年的历史。Dalton 根据水面蒸发形成原理和维持机理,综合考虑风速、气温、湿度对蒸发量的影响,提出了Dalton 模型,该模型对近代蒸发理论的创立起到了决定性的作用。我国自1950年代后期也开展了水面蒸发的研究,目前已经提出了很多水面蒸发的经验公式[13]。
Ashton[1]总结前人研究,认为只有两个蒸发公式可以应用于负气温条件下,一是Rimsha 和Don⁃chenko 提出的俄罗斯冬季公式,另一个是由Ryan-Harleman 提出的公式,并指出只有俄罗斯冬季公式应用于实际,在北美和冰岛的长期应用中,效果很好。我国东北地区也有学者采用俄罗斯冬季公式[14]。陈惠泉等[15]理论分析和实验验证表明,Ryan-Harleman 公式比较适用的条件是没有风速和虚温度>5℃(近似为),但是,对于冰封河湖,常常小于5℃。后来,也有一些专家学者提出了新的或改进的水面蒸发公式,例如陈惠泉[15]、李万义[16]等。不过,陈惠泉和毛世民公式主要针对发电厂冷却水系统,李万义公式没有考虑水面和大气温差的影响。 现有的研究表明温差对蒸发的作用很大,不容忽略[15]。
基于俄罗斯冬季公式,蒸发的热通量可描述为[1]:
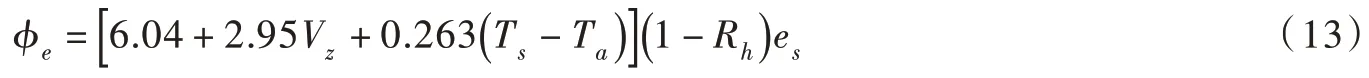
式中:ϕe为蒸发的热通量,W/m2;Vz为距离河湖表面1.5 m 处的风速,m/s。
根据Bowen 对流与蒸发的关系,河湖表面对流的热通量是:
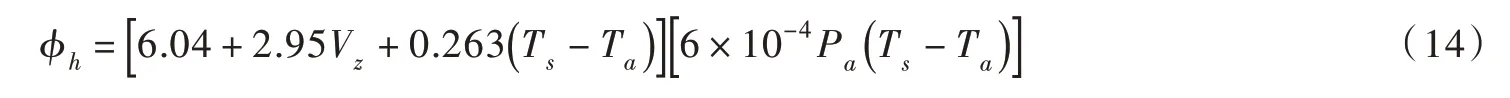
式中:ϕh为对流热通量,W/m2;Pa为当地大气压,hPa,随海拔高程增加而减小。
由式(13)和式(14)可见,Vz在蒸发和对流热交换过程中的影响很大,因此,气象站风级的观测资料能不能应用于河湖冰情计算分析是一个引人关注的问题。为此,在2016年1—4月在漠河北极村黑龙江岸边进行了风速的实测。如图10所示,漠河气象站2016年1—4月风级在2 级和10 级之间,理论平均风速与风级的计算公式是:

式中N 为风级,所以漠河理论风速Vm在2.4~26.5 m/s 之间,但是,由于漠河属于山区,实测黑龙江边瞬时最大风速Vz≈5.3 m/s,日平均风速Vz在0.13~1.9 m/s 之间,1月至4月的平均风速Vzm=0.77 m/s,远远小于理论风速。由此,可得重要结论:气象站风级或者风速资料一般不能正确估计地势低洼河面1.5 m 的风速,主要原因是气象站一般建立在地势较高、通风好的地方,而河道地势低,通风较差。
河道冰随时间的发展过程,除冰盖形成初期和开河外,是一个比较平稳的过程,短暂大风速对长期冰情发展影响有限。当以冰期平均风速评估风对蒸发和对流的影响,由于漠河冰期平均风速Vz≈0.77 m/s,所以风速影响占比为:。
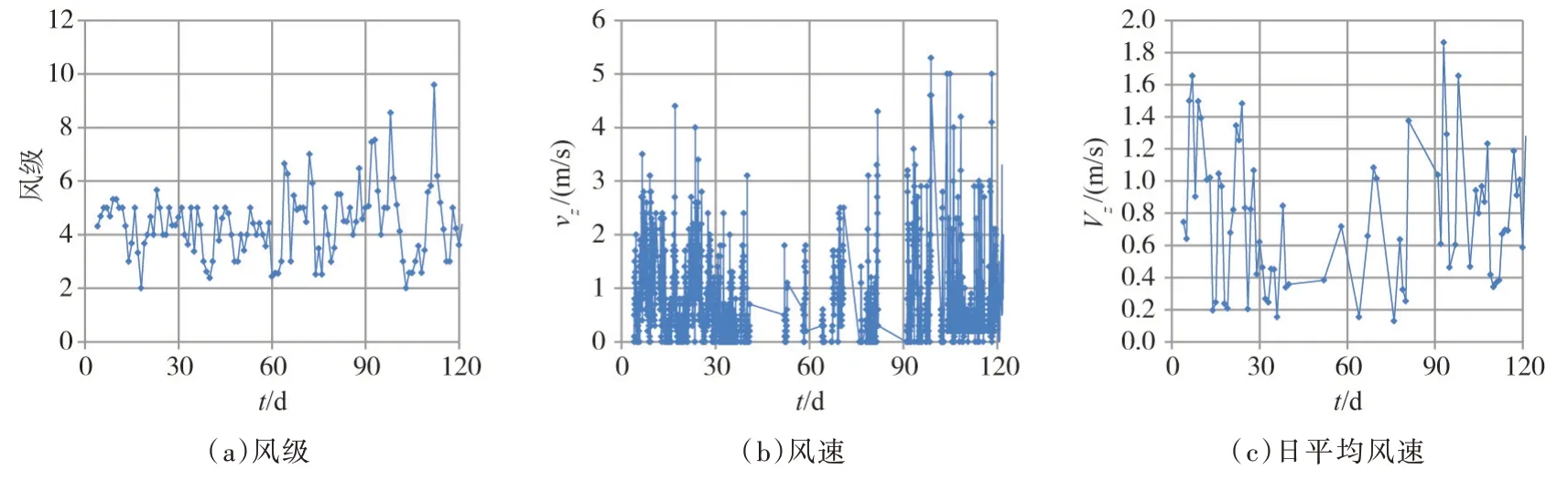
图2 2016年1月—4月漠河气象站风级与北极村黑龙江边实测瞬时风速和日平均风速
5 河湖与大气的热交换模型
河湖与大气的净热交换,包括太阳辐射、长波辐射及蒸发和对流是:

式中:ϕn为河湖表面日平均净热通量,W/m2;为太阳辐射净热通量,W/m2,asm为太阳辐射的日平均反照率。当遇到降雪天,上式中还需要增加降雪热通量ϕP[1]。我国东北、西北、内蒙古和青藏高原等地区,冬季,甚至春季,降雪频繁且降雪量较大,冰封河湖雪盖反照率asm对气候变化和冰厚变化具有很大影响[19-20]。新雪覆盖的冰的表面的反射率asm约为0.9,由雪冰组成的冰盖的反射率为0.6~0.8,与此形成对比的是,由清澈的柱状冰(黑冰)组成的冰盖的反射率可能较低,只有0.2,可以采用杨开林[9]提出的水冰雪太阳辐射反照率的通用模型估计。
当天气资料齐全,包括表面温度Ts、气温Ta、云量C、相对湿度Rh、风速Vz、当地大气压Pa等,云天太阳辐射ϕsc、大气长波逆辐射ϕa、河湖长波辐射ϕb、蒸发ϕe和对流ϕh分别采用式(6)(9)(10)(13)(14)计算。
6 河湖与大气热交换模型的线性化
虽然我国一些地方正在建立冰情观测站,例如南水北调工程和黄河冰情观测站,但尚无测站能够提供全面定时观测Ts、Ta、C、Rh、Vz、Pa随时间变化的资料,因此,如何把河湖与大气的净热交换多参数非线性模型式(16)转化为只是两个自变量Ts和Ta的线性模型,且具有较高的精度,不仅具有重要的理论意义,而且具有广泛的实用价值。
在冰期,河湖表面存在下述情况:
(1)存在敞露水面,例如南水北调中线工程漕河渡槽,全年不封冻,在气温Ta<0℃的情况下,水温Ts→0℃,这时,敞露水面与大气的温差(Ts-Ta)较大,特别是寒潮天气,这种情况水面蒸发和对流模型不适合采用线性化模型,否则,可能产生较大计算误差;
(2)河湖表面冰封,气温Ta>0℃,这时雪面和冰面将融化,冰盖上会形成薄薄的水膜,甚至星罗棋布小水洼,称为水覆冰现象,这时,冰面上温度接近融点温度,但冰上水体温度Ts将趋近Ta;
(3)河湖表面冰封,气温Ta<0℃,甚至存在雪盖,雪盖或裸冰表面温度Ts与气温Ta的关系。
以下仅研究情况(2)和(3)。
肖建民等[14]在黑龙江省胜利水库测得冰面温度Tis=0.55Ta,白乙拉等[17]在黑龙江省红旗泡水库测得冰面温度Tis=0.26Ta-4.6。
在2016年1—4月上旬,笔者团队在漠河北极村黑龙江段实测了冰情,包括冰盖下水温、冰盖和雪盖内部和表面温度的垂向分布以及气温,如图3所示,其中:Tw为水温或冰盖、雪盖、气温;hi和hs分别为冰厚和雪厚;L 为太原理工大学研制的R-T-O 冰雪情传感器刻度。R-T-O 冰雪情传感器长200 cm,垂直江面穿透雪盖和冰盖放置,下端(图3(a))测量水温,中段测量冰温和雪温,上端(图3(b))测量气温Ta和雪面或冰面温度Ts。
根据图3,可得下述结论:
(1)当Ta<0℃时,冰盖和雪盖内部温度近似线性分布;雪盖表面温度Ts随着气温Ta的变化而变化,前者与后者的变化存在一定的时间滞后,Ts接近于Ta,相差约为1.0~3.0℃,如图3 中A 区和B区所示;
(2)当Ta>0℃时,雪盖逐渐消失,冰盖内部温度成非线性分布,如图3 中2016/4/11 曲线所示。
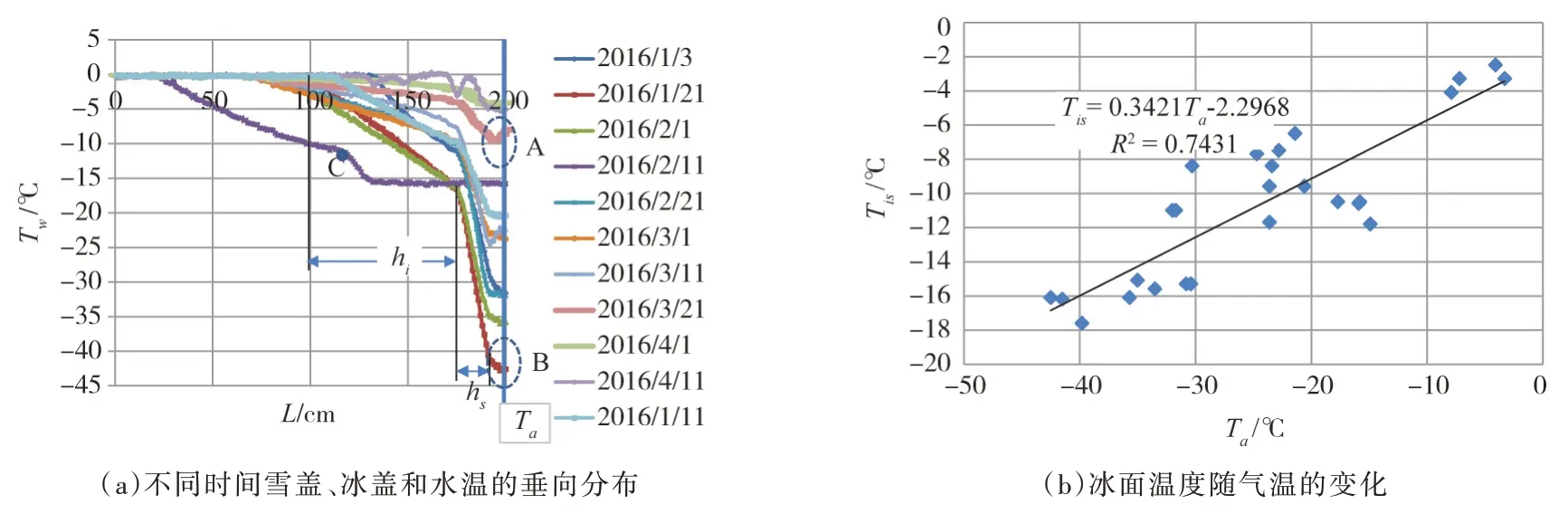
图3 实测漠河北极村黑龙江段冰情
(3)当Ta<0℃时,雪盖下冰面温度Tis(如点C所示处)远远大于气温Ta,根据3 个观测点的数据,线性回归得Tis≈0.3Ta-2.30 ,这表明雪盖具有很好的保温作用,雪盖下冰盖表面温度远远大于气温。
(4)11月至4月初,冰盖上都有较厚积雪,且冰盖下水温约等于0℃。
由于胜利水库、红旗泡水库、漠河均属于黑龙江省,冰封期降雪频繁,冰面上厚雪覆盖,由上面结论(3)可以判断出肖建民等[14]和白乙拉等[17]测得的冰面温度与气温关系仅适用于雪盖下冰面温度。
综上所述,由于冰封河湖表面温度Ts接近Ta,包括裸露冰盖表面,这就产生一个思路,在Ts=Ta点将式(16)线性化,即:


当假设Ts=Ta是河湖表面的平衡温度,即,则式(17)可简化为Ashton[1]形式的线性化模型:

对长波辐射式(9)和式(10)在Ts=Ta求偏导数,得:
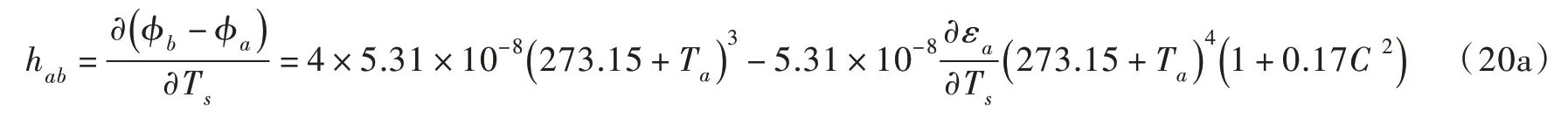
由式(11)和式(12)分别得:
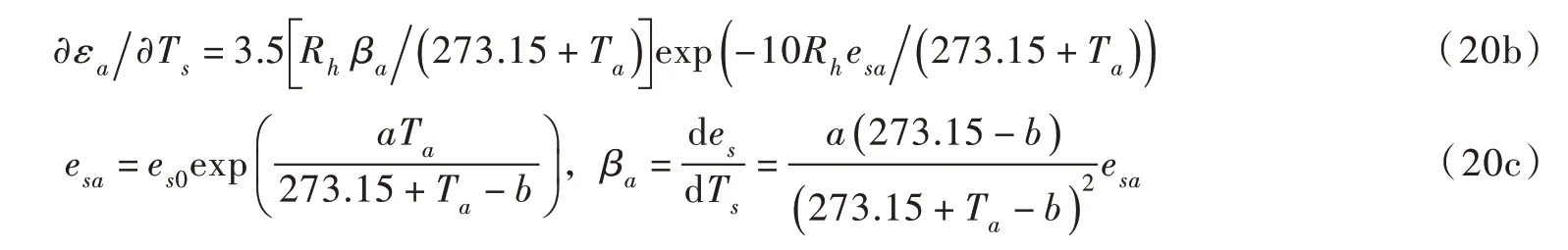
对蒸发和对流式(13)和式(14)在Ts=Ta点求偏导数:
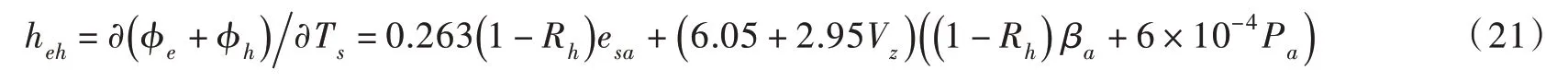
由于Ta、C 和Rh是相互独立且随时空变化,鉴于此,下面将研究利用气象站历史日平均天气资料获得热交换系数hsa的方法。需要说明的是,气象站历史天气资料Ta、C 和Rh与河湖实际情况是存在一定差异[18],但其长期统计特性是比较接近的。
令式(21)中风速Vz=0,可得图4 和图5所示北京地区2015.12.1—2016.2.29 与2016.12.1—2017.2.29两个冰期hsa的线性回归经验式:
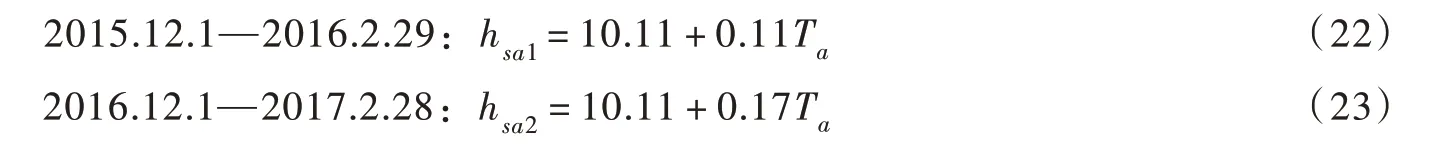
相关系数R2=0.21~0.33,线性相关性一般。
式(22)—式(23)得:
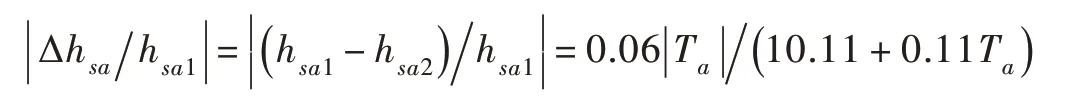
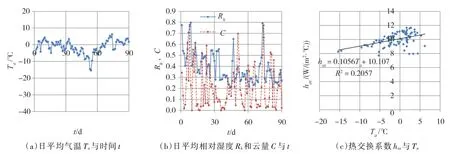
图4 北京2015.12.1—2016.2.29日平均天气资料及ϕsa0 和hsa 的线性回归
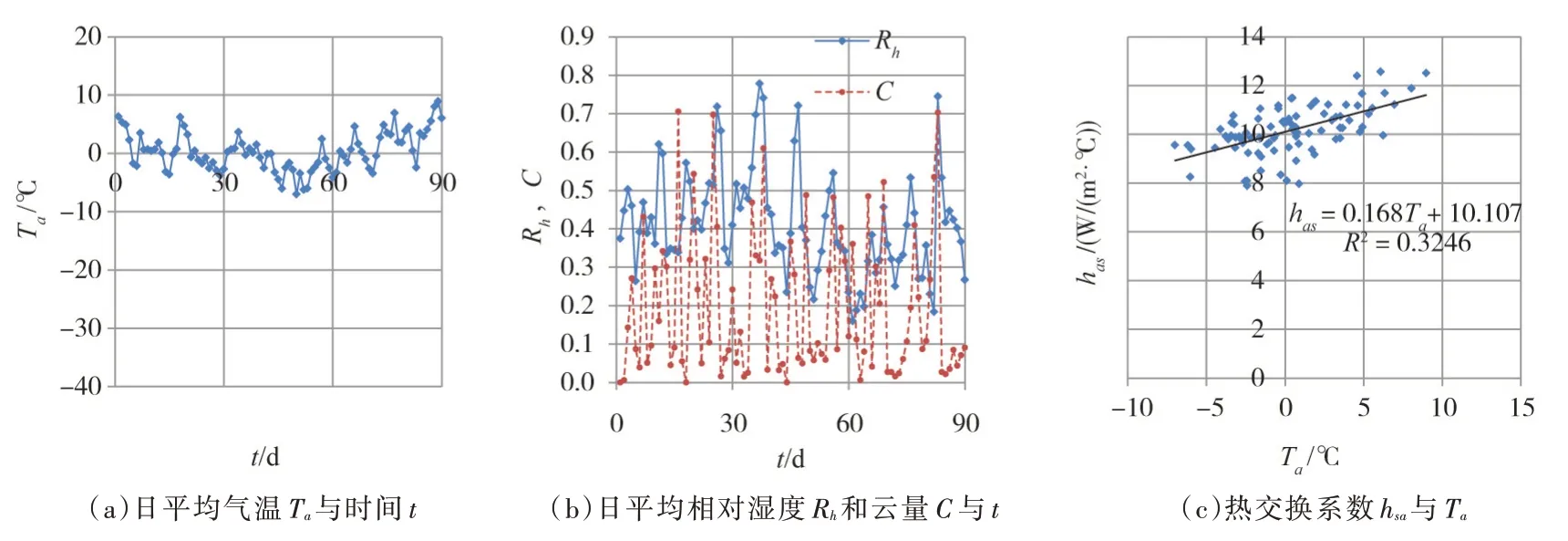
图5 北京2016.12.1—2017.2.28日平均天气资料及ϕsa 和Ta的线性回归
采用与上类似的方法,可得一些其他地区hsa与Ta的线性关系。表1 中列出了一些典型地区,包括漠河、沈阳、包头、北京、保定、拉萨的天气特征及不同风速Vz时hsa的线性公式,其中风速假设为冰期日平均风速。黑龙江漠河是我国纬度最大、气候最寒冷、湿度大、云量大、冰期时间长的地区,hsa的平均值最小;包头属于内蒙古高原,气候干燥,少云,冰期较长;西藏拉萨纬度小,空气干燥、少云、冰期时间长,但大气压较低,hsa的平均值较小;沈阳、北京、保定属于平原地区,常年大气压较高,位于我国的中部和北部,空气干燥、少云,冰期时间较短,但hsa的平均值较大。
根据表1 可得下述结论:(1)河湖与大气的热交换系数hsa与日平均气温Ta成正比;(2)当已知Vz=0.0 m/s 时的热交换系数hsa0,则不同风速的热交换系数可描述为:
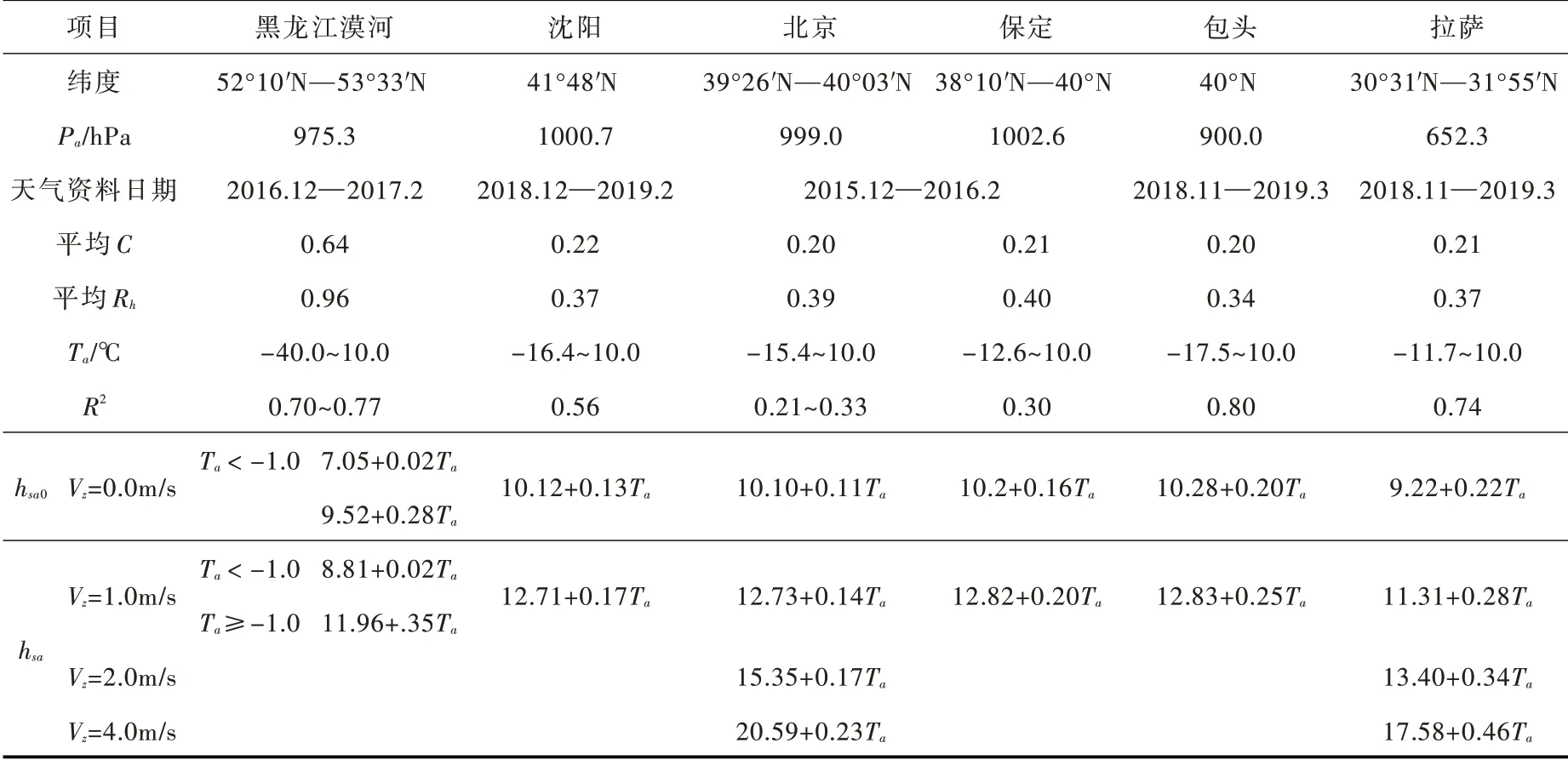
表1 典型地区气象特征参数及河湖与大气热交换模型的线性化结果

由于北京、保定、沈阳、包头冰期日平均气温Ta=-17~10℃之间、云量C=0.20~0.22、Rh=0.37~0.40,hsa的值相差不大,可以采用统一的参数,当Vz=0.0 时,hsa0约为10.0 W/m2·℃。漠河和拉萨的hsa略小于北京等地区的,前者是因为冰期相对湿度较大,后者是因为海拔高程较高。
7 结束语
基于原型冰情观测和现有研究成果,建立了适用于冰期河湖与大气的热交换数学模型。太阳辐射现场观测资料证明本文提出的计算晴天日射的模型及大气平均透明系数和光学大气质量的方法是实用的。实测风速与气象站风级或者风速资料的对比表明两者差别很大。当气温Ta<0.0℃时,冰盖和雪盖内部温度近似线性分布,且雪盖下冰面温度Tis≈0.34Ta-2.30 ,但是雪盖或裸露冰盖表面温度Ts接近于Ta,因此在Ts=Ta点将河湖与大气的热交换模型线性化是最好的近似。对于一个地区,采用典型年历史日平均天气资料得到的热交换系数hsa0可用于预测其他年的热交换。 hsa与Ta成正比,当已知风速Vz=0.0 时的热交换系数 hsa0,则不同风速的热交换系数。北京、保定、沈阳、包头的平均hsa0≈10.0 W/(m2·℃),漠河和拉萨的hsa略小于北京的。

