GWLS-SVR模型的红枣树叶片叶绿素含量估算
尼格拉·吐尔逊, 苏磊·乃比, 高 健, 沈江龙, 郑江华*, 余丹林
1. 新疆大学资源与环境科学学院, 新疆 乌鲁木齐 830046 2. 新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046 3. 新疆林业科学院现代林业研究所, 新疆 乌鲁木齐 830063 4. Department of Earth and Environmental Studies, Montclair State University, New Jersey 07043, USA
引 言
叶绿素含量是枣树光合作用能力、 生长状况、 营养状况的指示剂[1], 通常采用便携式叶绿素计(SPAD-502)测定植物叶片SPAD值来直接表征植物叶绿素含量的相对大小, 但使用过程中需要将叶片反复插入测量, 难以用于大范围的叶绿素检测, 研究表明SPAD值能与无损、 无污染、 价格低的高光谱遥感数据准确对应, 近年来成为叶绿素含量估算的强有力工具[2]。
20世纪90年代, Pinar[3]和 Blackburn[4]等研究得到叶绿素与高光谱波段之间的相关关系。 随后, 许多学者在高光谱估算叶绿素模型方面开展了大量的研究, 杜华强基于高斯核函数变换的偏最小二成回归模型建立了马尾松针叶叶绿素含量与光谱反射率及9个特征参数之间的预测模型, 其精度远大于传统线性回归模型[5]。 刘京等用实例证实了支持向量机具有更好的SPAD值反演效果[6]。 冯海宽等基于特征光谱参数, 利用随机森林模型较好的估算了苹果叶片叶绿素[7]。 李晓丽等证实了最小二乘支持向量机(least sqares support vector regression, LS-SVR)在植物参数估算方面具有较好效果[8]。
上述研究常选用相关系数较高的波段或者植被指数建模使得变量选择随机、 单一、 缺乏定量化, 模型估算能力低下。 本文通过CP统计量在预测角度选择重要性较高的自变量, 筛选重要程度高的特征波段(characteristic band, CB)。 其次, 以往的高光谱估算应用广泛的多元线性回归(multiple linear regression, MLR)、 支持向量机(support vector regression, SVR)、 LS-SVR模型较多, 并没有考虑到地理位置可能对叶片SPAD值产生的影响。 2017年Hwang和Shim对于LSSVM模型加入地理位置影响, 提出了地理加权最小二乘支持向量机模型[9](GWLS-SVM), 证实了其估计精度显著高于传统的GWR、 LS-SVR模型。 本研究对于GWLS-SVR模型是否适用于叶绿素含量估算, 能否在红枣树叶片叶绿素估算中得到较好效果还需要进一步的验证。 用CP统计量选择特征波段, 计算若羌红枣树叶片SPAD值的全局莫兰指数, 分析红枣树叶片SPAD值分布是否与空间位置有关, 再运用GWLS-SVR模型, 将建模结果与传统模型进行对比分析, 检验并比较模型的拟合效果。
1 实验部分
1.1 研究区概况及采样点布设
研究区位于中国新疆若羌县, 范围在东经87°00′—89°0′、 北纬38°40′—39°30′之间, 属暖温带大陆性荒漠干旱气候, 是新疆名牌产品“若羌红枣”种植区[10]。 于若羌红枣果实成熟期2019年9月28日—10月2日采样, 为了保证实验结果的全面性和精确性, 在去除野外数据异常值后最终保留均匀覆盖若羌县的67个枣林样点, 在预先设计的枣林内确定代表性枣树1~3棵进行数据采集, 再通过手持GPS记录地理位置信息, 共采集219条红枣树叶片高光谱数据和219个枣树叶片SPAD值数据, 研究区位置和采样样点地理位置分布情况如图1。

图1 研究区位置和采样点分布图
1.2 红枣树叶片光谱测定与处理
红枣树的叶片光谱反射率在晴朗无风无云条件下于北京时间11:00—17:00使用PSR-3500便携式地物光谱仪在野外测定, 波段范围是350~2 500 nm, 每隔1 nm输出一个数据, 一共2 151个光谱通道。 在选择的代表性1~3颗枣树上、 中、 下层各随机采集3片叶片。 为减少误差, 每次光谱测定之前均进行白板标定, 同时用干燥纸巾去除叶片表面浮尘, 测量时将叶片铺平放置在反射率近似为零的黑板上, 将光纤探头垂直固定于叶片上方约5 mm, 每个叶片样本避开叶脉重复测量3次, 取光谱曲线的算术平均值作为该样点的原始叶片光谱反射率。 为减少噪声影响, 剔除1 050~2 500 nm噪声较大波段, 并利用Origin软件平滑去噪[11]。 另外, 导数光谱可以反映植被中生化物质的吸收引起的波形变化还能够揭示光谱峰值的内在特征进而估算植被内部叶绿素含量信息[2]。 因此, 对原始光谱反射率(raw reflectance, RR)求光谱一阶导数(first derivative of reflectance, FD)。
1.3 SPAD值测定
使用叶绿素计(SPAD-502Plus, Konica Minoita, Japan)对现场采集的多个枣树叶片SPAD值进行测定, 测量时避开叶脉部分, 从叶柄至叶尖分段随机测量3次, 将多个叶片测定结果取算术平均值作为该样点SPAD值。 SPAD值测定时间与叶片光谱测定同步进行, 测定位置与叶片光谱保持一致。
1.4 变量选择
本工作采用CP统计量进行变量选择。CP统计量可以通过预测的角度选择重要性较高的自变量。 其原理为由部分变量预测的均方误差可能比利用所有变量进行预测的均方误差更小, 故可以去除重要程度不是很高的变量。 其计算方式如式(1)
(1)

1.5 地理加权最小二乘支持向量回归模型(GWLS-SVR)
f(xi,Ui)=ωTφ(xi)+bi
(2)
设给定x与Ui下的权重矩阵为Wi, 则可以将回归模型转化成如式(3)优化问题
(3)
其中, C>0为惩罚参数, wij为用于表示Ui和Uj之间的距离的权重函数。

(4)

2 结果与讨论
2.1 不同范围SPAD值红枣树叶片平均光谱反射特征
图2是不同范围SPAD值的红枣树叶片平均光谱反射率曲线图。 由图可知, 不同范围SPAD值的红枣树叶片平均反射率曲线变化趋势基本相同。 总体上, 350~750 nm波段内反射率比750~1 050 nm波段低。 在350~675 nm波段内随着SPAD值的升高, 红枣树叶片平均光谱反射率降低, 光谱差异较明显, 其中, 在500~551 nm波段范围内反射率缓慢上升, 551 nm附近出现反射峰, 675 nm附近出现吸收谷; 675~750 nm处平均光谱反射率随着波长呈现快速上升趋势, 750~1 050 nm范围内, 随着SPAD值的升高, 平均光谱反射率升高。 红枣树的长势状态直接决定了SPAD值的大小, SPAD值也会影响红枣树叶片的反射率。

图2 不同范围SPAD值红枣树叶片平均光谱反射特征
2.2 红枣树叶片光谱和SPAD值相关性分析
为了明确红枣树叶片SPAD值相对应的敏感波段, 将红枣树叶片SPAD值和原始光谱、 光谱一阶导数反射率波段做皮尔逊相关性分析。 由图3可知, 红枣树叶片SPAD值和原始光谱反射率及光谱一阶导数反射率紧密相关, 且都存在着极显著相关。 对原始光谱来说, 在570~620及690~700 nm间达到相关系数峰值, 通过了0.01的显著性水平, 相关系数分别达到-0.578及-0.561, 此波段范围受叶绿素吸收的影响, 相关系数呈负相关, 选择这两组波段的原始光谱反射率作为估测枣树叶片SPAD值的敏感波段区间。 SPAD值与光谱一阶导数呈正负相关, 相关性极显著的波段分布在400~750 nm区间内, 最高值出现在688 nm处。 与原始光谱相比, 在492~510, 542~543, 642~652, 657~670和682~692 nm区间内的SPAD相关性有所提高, 且分别达到-0.655, -0.662, -0.697, 0.709和-0.749, 也说明了这些波段的光谱反射率与枣树叶片SPAD值相关性好, 适合用于敏感波段的挑选。 综上所述, 红枣树叶片反射率光谱做一阶导数处理后与SPAD的相关性有较显著的提高。
2.3 变量选择
结合图3, 在原始光谱570~620 nm范围内选择了相关性高的581, 590, 595和602 nm波段, 690~700 nm波段范围内选择695和696 nm共6个特征波段进行CP统计量的计算; 基于光谱一阶导数与SPAD值相关性高低, 在492~510, 542~543, 642~652, 657~670和682~692 nm共5个波段内分别选择相关性达到区间内最高的495, 543, 649, 664和688 nm共5个特征波段计算出其不同组合统计量, 表1为波段的相关系数表。
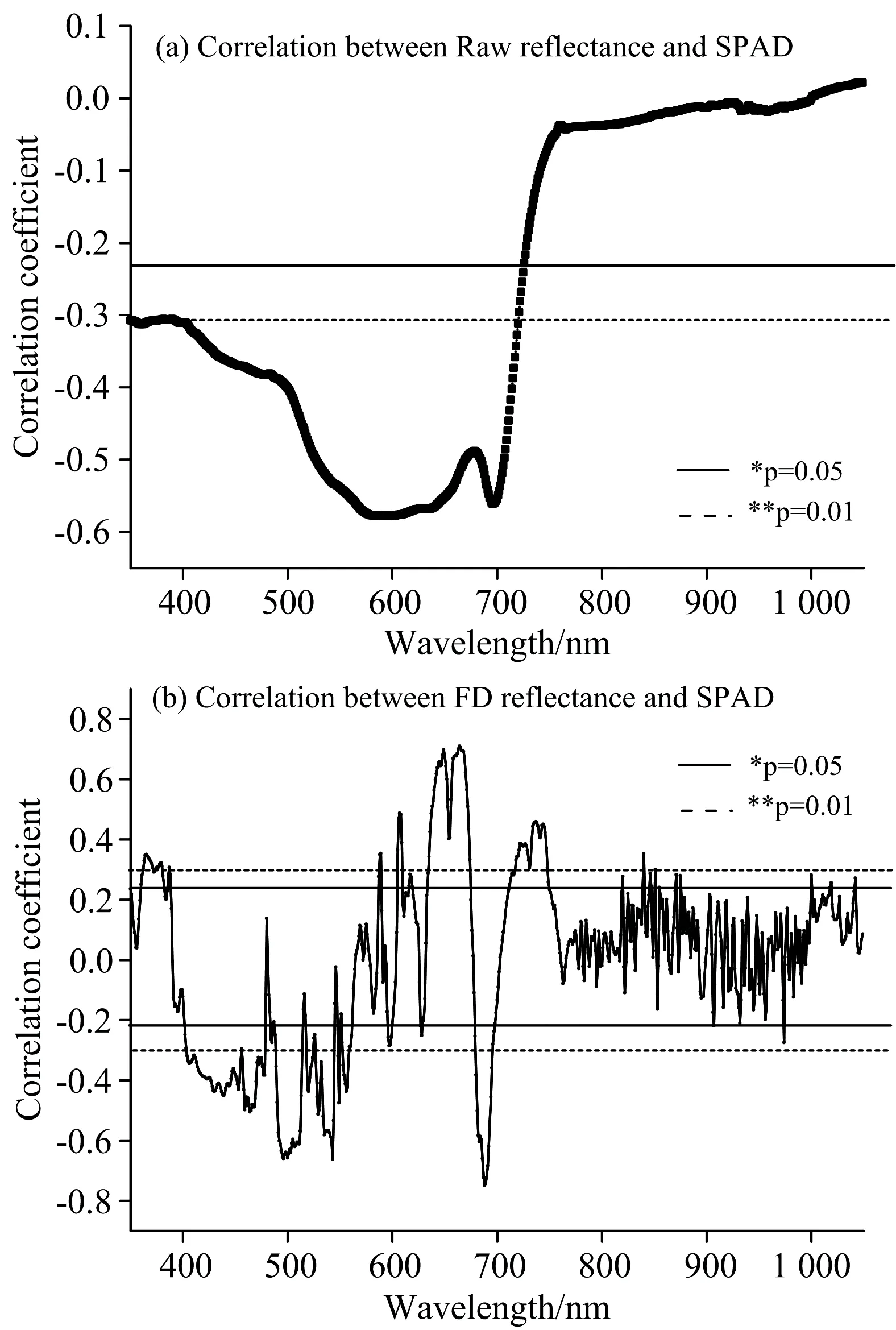
图3 SPAD值与光谱反射率之间的相关性
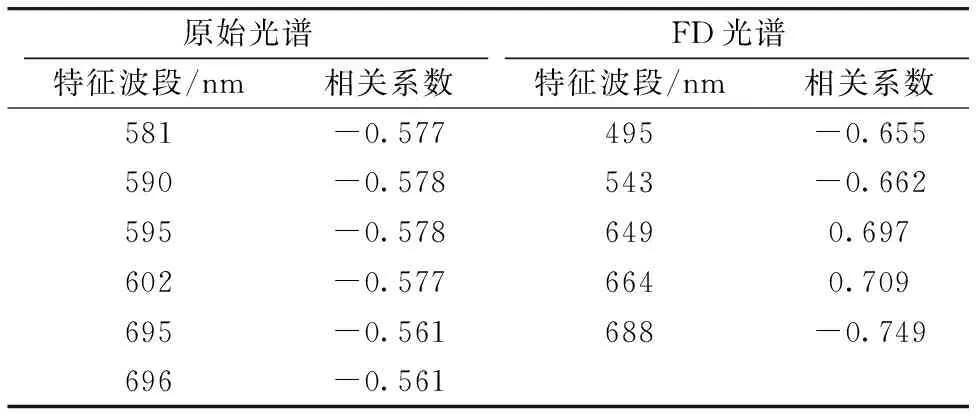
表1 波段的相关系数表
表2为CP统计量计算结果表, 考虑到所有变量组合方式数目较大, 且大部分组合方式的CP统计量都远高于表2中的几种组合方式, 只列出CP统计量值靠前的组合。CP统计量越低, 代表该种变量选择方式重要性程度越高。 且由表2可知, 原始光谱选择在570~620和690~700 nm范围内分别选择595和696 nm时CP统计量绝对值最低, 因此将595与696 nm原始光谱重要程度最高的两个变量作为建模的特征波段。 光谱一阶导数变换后688 nm波段CP统计量绝对值最低, 因此光谱一阶导数的特征波段定为688 nm。 原始光谱特征波段696 nm和光谱一阶导数特征波段688 nm都处于红边波段[13], 说明红边与植被的各种理化参数是紧密相关的, 是描述植物色素状态和健康状况的重要的指示波段。

表2 特征波段组合及CP统计量计算结果
不难发现, 对于同一个区间的波段组合总有单波段的CP统计量低于多波段组合的CP统计量。 说明相近波段组合建模会使得误差增大, 这可能是相近波段之间较强共线性造成的, 故每个敏感波段区间只选取一个波段进行建模是合理的。
2.4 模型的构建与检验
运用CP统计量选出的3个特征波段以及实测叶片SPAD值建立MLR, SVR和GWLS-SVR模型。 相比较而言, GWLS-SVR主要的优势是变量系数随着地理位置而变化, 具有较强的灵活性。 为了明确红枣树叶片SPAD值分布是否与地理位置有关, 对其进行Moran’s Ⅰ的计算结果为0.125 8(p<0.1), 呈空间正相关, 说明枣树叶片SPAD值的分布有显著的空间聚集性, 适合运用GWLS-SVR模型来建模。
原始光谱(RR)与光谱一阶导数(FD)分别基于MLR, SVR以及GWLS-SVR拟合的MSE与R2如图4所示。 从建模效果来看, 基于原始光谱建立的三种模型中, MLR与SVR的R2低于0.8, MSE也较高, 说明这两种模型的稳定性较差, 预测效果不理想; GWLS-SVR的R2为0.915, MSE低至3.679, 表明GWLS-SVR的稳定性及估算能力优于MLR与SVR模型。 光谱一阶导数变换后的三种模型精度较原始光谱均有所提升, 且MSE整体上都有所降低, 表明数据变换后模型的稳定性和精度有了一定的提高; 而GWLS-SVR在光谱一阶导变换后均显著优于其余两种模型, 模型的R2提高到了0.975, MLR与SVR的MSE均比GWLS-SVR高约20倍, 综合上述可得GWLS-SVR模型不仅拟合精度高, 其估计偏差与方差综合看来均低于其余两个模型。
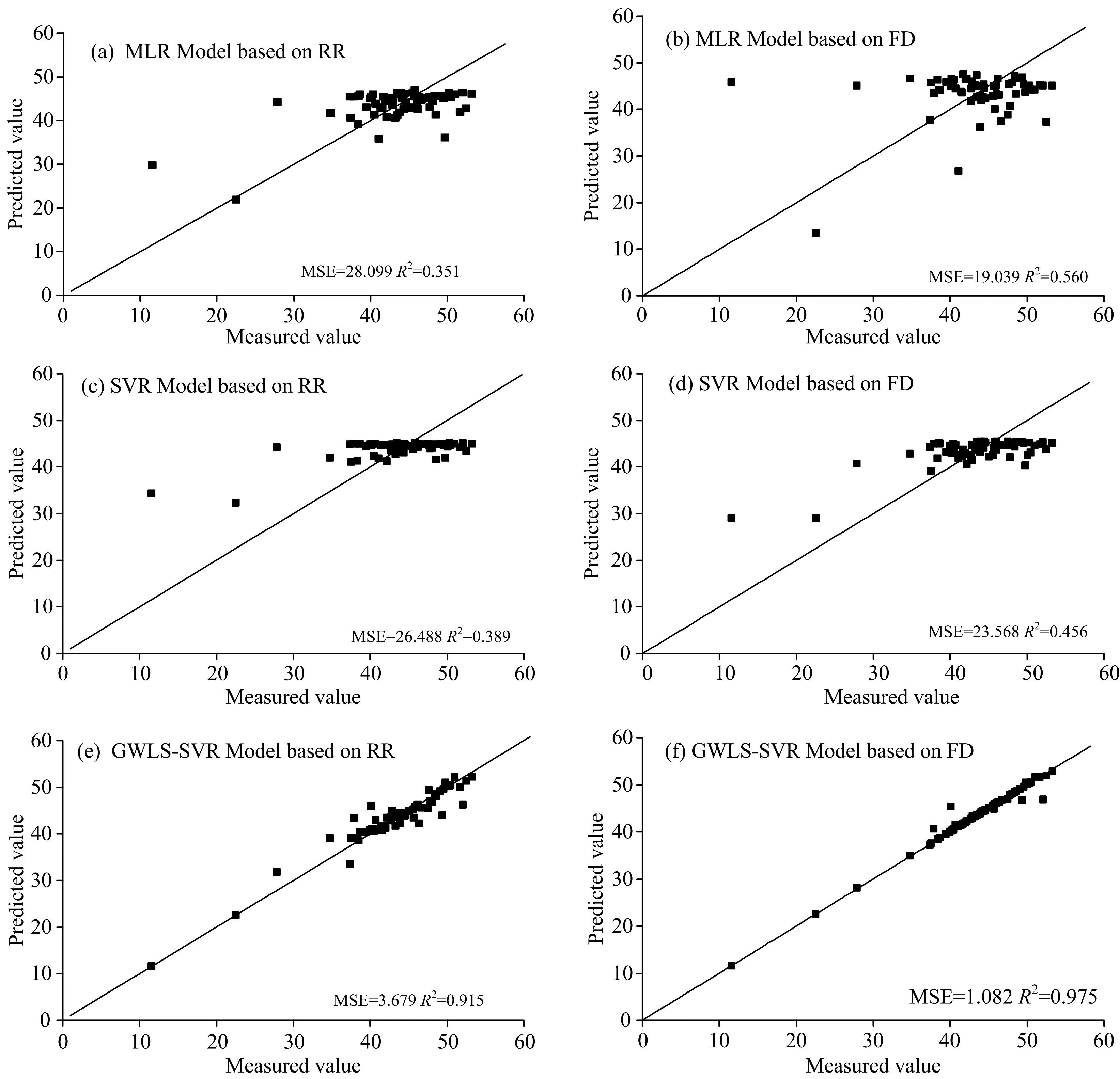
图4 MLR, SVR和GWLS-SVR对实测值与预测值间的拟合图
从拟合效果来看, GWLS-SVR在原始光谱与光谱一阶导数的拟合曲线比起其他两种模型真实值与预测值均匀分布在1∶1直线周围, 表明GWLS-SVR的拟合效果较好, 且在光谱一阶导数变换后的拟合效果更佳。
为了检验三种模型的拟合效果差异, 对于原始样本利用Bootstrap再抽样方法进行100次有放回随机抽样, 每次抽取67个样本。 之后对于随机生成的样本利用上述三种模型分别建模计算100组MSE的均值(mean of MSE)和方差(varionce of MSE), 并利用配对t检验进一步比较原始光谱和光谱一阶导数基于GWLS-SVR与其他两个模型的MSE之间的差异的显著性。
100次Bootstrap再抽样并基于三种模型建模后的MSE箱线图如图5所示。
由表3及图5可以看出, 整体上GWLS-SVR的100组MSE在原始光谱与光谱一阶导变换后均为最低, 且波动也比较小, 说明100次Bootstrap再抽样后GWLS-SVR相比于传统的MLR及SVR模型预测的精度较高且发挥比较稳定, 其中基于光谱一阶导数建立的GWLS-SVR模型的MSE最小, 且波动最小, 说明基于光谱一阶导数建立的GWLS-SVR模型的模型预测精度最佳且稳定。
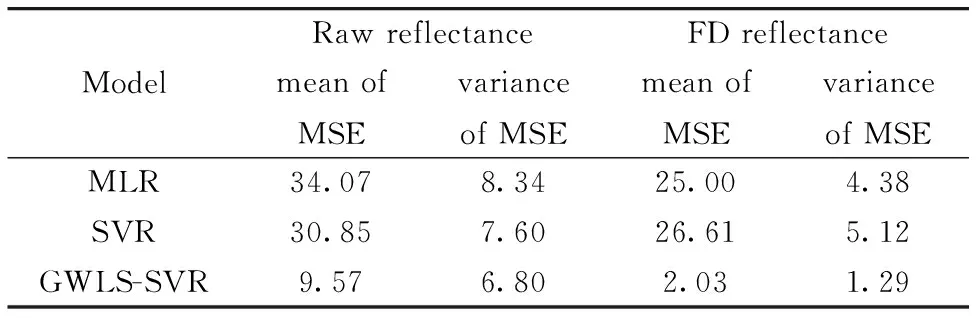
表3 Bootstrap再抽样结果
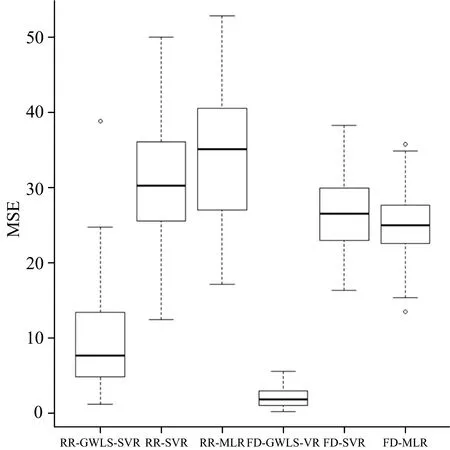
图5 100次建模的MSE箱线图
为了进一步检验GWLS-SVR的MSE是否显著小于其他两个模型的MSE, 以下分别做GWLS-SVR与其他两个模型的单边配对t检验。 所得T统计量与p值如表4所示。
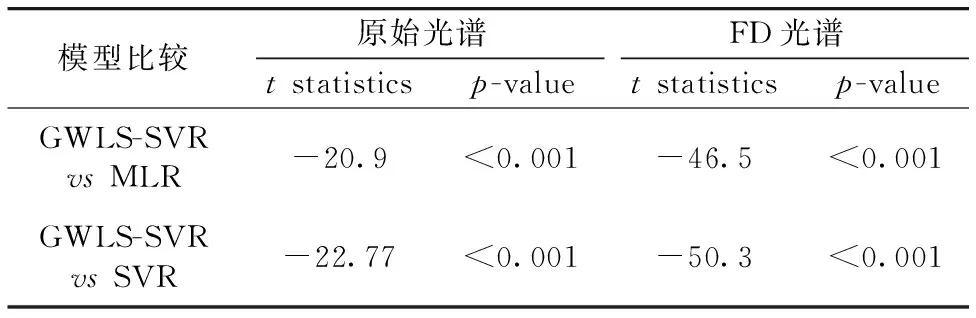
表4 t检验结果
由表4可见, 4组单边配对t检验的t统计量的绝对值都比较大, 且p值均非常接近0。 所以GWLS-SVR预测的MSE小于其他两个模型的MSE这一假设在统计学上是高度显著的。
3 结 论
利用野外实测67个样点, 219条红枣树叶片高光谱数据和枣树叶片SPAD值数据, 对SPAD值与高光谱波段进行相关性分析、CP统计量特征波段选取、 建立基于特征波段的SPAD值估算模型, 结果表明:
(1)光谱一阶导数起到了对原始光谱数据的去噪、 突出高光谱信息的作用, 尤其是在492~510, 542~543, 642~652, 657~670和682~692 nm区间内明显提高了与SPAD值的相关性。
(2)根据统计量计算发现: 对于同一个敏感波段区间的波段组合总有单个波段的CP统计量低于多个波段组合的CP统计量, 临近分布的波段之间的存在的较强共线性可能导致这些波段的组合误差增大。
(3)基于实地采样数据进行地统计分析若羌县枣树SPAD值与地理位置的关联性, 发现若羌县存在空间聚集性, 全局莫兰指数为0.125 8(p<0.1), 表明地理加权最小二乘支持向量机方法适用于估算若羌县枣树叶片SPAD值。
(4)基于光谱一阶导数的特征波段建立的GWLS-SVR模型的估算能力(R2为0.975, MSE为1.082)优于基于原始光谱特征波段建立的GWLS-SVR模型(R2为0.915, MSE为3.679), 且由结合Bootstrap再抽样方法与t检验的结果来看, 基于光谱一阶导数的加入地理位置信息的GWLS-SVR模型为最优的枣树叶片SPAD值估算模型, 能够为快速无损的监测红枣树生长状况提供参考。
致谢:感谢若羌县委的一贯支持, 感谢若羌县委办、 县农业农村局、 自然资源局、 交通运输局对本项野外调查工作的具体帮助。 感谢县委办户亮亮同志对本项工作的协调和帮助。

