基于VaR理论的综合能源零售市场最优策略

郭祚刚，徐敏，李睿智，袁智勇，谈赢杰，陈柏沅，雷金勇，刘念

(1.南方电网科学研究院，广州市 510663；2.新能源电力系统国家重点实验室(华北电力大学)，北京市 102206)

0 引 言

能源互联、绿色低碳、高效利用是未来能源发展的方向，为解决能源危机，有效提高能源的利用效率，开发新能源并加强可再生能源的综合利用，综合能源系统( integrated energy system，IES)应运而生[1]。综合能源系统在能源供给-传输-使用-存储多个环节深度耦合，能源系统的主体、物理可行域、运行目标、风险相较传统分立能源系统发生了极大变化[2]。文献[3]计及热网、气网的动态储能特性，提出了一种电-气-热综合能源系统优化调度模型。文献[4]将条件风险价值(conditional value at risk，CVaR)理论引入IES调度运行问题，建立了一种考虑可再生能源发电侧以及电、热负荷侧不确定性的综合能源系统经济调度模型。文献[5]提出一种考虑综合能源系统的配网嵌层规划模型。

随着能源市场化改革推进，传统集中式调度逐步被市场化交易取代，需求侧参与系统运行程度加深。电力市场按照空间分布可分为跨区级批发市场、区域级批发市场、配网级零售市场。热力因难以长距离传输，具有较强的区域垄断性，是市场化程度最低的能源，其最大规模为以集中供热为核心的城市级区域热网，需求波动较小，以日前市场为主。多热源联网的提出使得热力市场化空间进一步提升，其仿照电力市场设计的源-网分开供热模式是未来热力市场的形态[6]。其中区域批发市场的参与主体主要是能源生产侧与能源服务商，其交易按时间尺度分为中长期和现货交易。综合能源系统的多能物理耦合将逐步产生价格上的耦合，单一能源的市场定价方式会扭曲多能价格信号，无法指导综合能源系统高效运行[6]。目前针对多能市场的研究多集中于区域级综合能源系统。文献[7]统一电-热交易，提出了基于联合出清机制的综合能源系统现货市场。文献[8]探究了电力-天然气市场的协调机制，并研究了耦合市场中电力、天然气供应商的竞争均衡问题。文献[9]基于合作博弈提出了工业园区综合能源系统的成本分摊和收益分配方法。

然而多能零售需求侧作为综合能源系统灵活性资源的重要来源，相关研究较少。零售市场研究多针对电力零售市场。文献[10]对英国、美国德州及北欧电力市场的交易结算机制进行了对比分析。文献[11]总结了德州电力市场的市场主体机构、零售商业务范围，并给出了固定费率套餐、可变费率套餐、指数费率套餐计算公式。配网级零售市场对象既有城市级配网也有较为独立的工业园区，交易机制根据配网对象实际情况更为灵活，既有分布式能源的P2P交易[12]，也有售电公司多样化的零售套餐，产消角色、能源价格制定均有较大的灵活性。目前，国内外对于能源零售商的定价策略研究还很少，主要集中在电信领域的价格套餐制定[13-15]。除了价格制定的优化方法之外，也有部分学者研究了商品价格对消费决策的影响[16-18]。

本文提出一种综合能源服务商在配网级零售市场的静态定价策略，具体方法为：综合能源服务商在中长期阶段提前预测零售能源需求、批发市场能源价格、自身设备等因素，并承担预测偏离风险，制定覆盖自身成本、利润、风险的多能零售价格，并与用户签订多能零售供能合同。该静态零售价格在合同期内(通常以月度，季度为单位)无法变更，在日前阶段预测值确定后，综合能源服务商进行日前调度使得该静态零售价格下自身收益最大化。针对静态定价-日前调度两阶段问题，本文提出一种粒子群-线性规划算法求解该问题。

1 零售市场最优策略模型

相较价格实时改变的动态定价机制，本文零售定价机制采用静态定价机制，即零售价格通过中长期合同锁定，在合同期内(通常以月度、季度为单位)不再变更，适用于风险厌恶、无过多响应能力的用户。综合能源服务商满足零售用户负荷的供能方式主要有自身设备产能以及现货能源市场购能。其中，自身供能设备主要有热电联产(conbined heat and power，CHP)机组以及燃气锅炉，其分别将在现货天然气市场购买的天然气转化为电能和热能。综合能源服务商最优策略分为两阶段，第一阶段为中长期策略，综合能源服务商需提前预测零售能源需求、批发市场能源价格波动，并承担预测偏离实际的风险，制定覆盖自身成本、利润、风险的零售价格，并与用户签订供能合同锁定零售价格。第二阶段为日前阶段策略，现货价格、用户负荷在日前确定后，综合能源服务商进行日前调度，调整供能设备出力，使得在第一阶段锁定的静态零售价下，自身收益最大。

1.1 随机性模型

综合能源服务商通过现货市场购能和自身分布式供能设备满足零售负荷需求。在中长期决策阶段，随机性来源于两方面，其一为电、热零售负荷的随机性，其二为现货价格的随机性。

电、热负荷作为零售市场最优策略的基本数据，很大程度上决定了策略结果。已有研究表明，不同时期的同一时段负荷大致呈正态分布[16]。零售用户负荷中长期预测值呈现以期望负荷为均值的有界正态分布。

零售用户电负荷分布：

(1)

同理，零售用户热负荷分布：

(2)

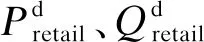
期望电负荷：

(3)

期望热负荷：

(4)

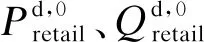
园区节点现货价格实际值呈现以中长期现货价格预测值为均值的有界正态分布。

园区节点现货电价分布：

(5)

同理，园区节点现货天然气价分布：

(6)

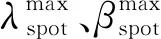
1.2 静态零售定价模型

静态零售定价模型为两阶段模型的第一阶段。综合能源服务商于中长期阶段考虑1.1节所述随机性，制定最优静态零售价格，并通过合同锁定。

本文采用风险价值(value at risk，VaR)来描述计及中长期不确定性的静态定价问题。VaR是指在市场正常波动条件和给定的概率水平(置信度)下用于评估和计量某一金融资产或证券投资组合在未来既定时期内可能遭受的潜在最大价值损失。本节VaR值含义是在一定置信度α下，园区综合能源服务商潜在日前最优调度值最大，具体如下所示：

Pr(Mday≥Vα)=α

(7)

式中：Pr(·)为分布函数；Vα即为置信度α下综合能源系统运营商的日前调度最优值的风险价值；Mday即为日前调度最优值，为一受现货价格和零售负荷影响的随机值。

综合能源系统运营商中长期的静态零售定价问题可描述为：

(8)

Vα∈arg{Pr(Mday≥Vα)=α}

(9)

φ(Mday)∈arg{φNc{D(nc)}}

(10)

λretail≤λretail,max

(11)

βretail≤βretail,max

(12)

式中：φ(Mday)为日前最优调度值的概率分布，依赖于求解Nc个典型场景下的日前最优调度问题φNc{D(nc)}；D(nc)表示典型场景nc的日前调度问题。

1.3 日前优化调度模型

日前优化调度模型为两阶段模型中的第二阶段。第一阶段的静态零售价格λretail、βretail为已知常数，现货价格及零售负荷在日前阶段按概率退化为常量，即日前调度场景按概率退化为某一典型场景。综合能源服务商通过调度优化现货市场购电量Pspot、现货市场购气量Gspot、微燃机耗气量GCHP和燃气锅炉耗气量Gboiler，使得自身综合效用fretail最大化，具体如下：

λspotPspot-δspotGspot

(13)

能量转换约束条件如下：

Gspot=GCHP+Gboiler

(14)

(15)

(16)

(17)

(18)

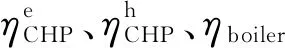
2 求解方法

由此，静态零售定价问题呈现为一个两阶段双层优化模型。其中，上层是综合能源系统运营商中长期静态零售定价问题，其目标是使得综合能源服务商日前优化调度最优值在置信度α下风险价值最大，上层的目标值Vα的获得依赖于求解Nc个典型场景下层日前调度问题，日前最优调度值的概率分布为φ(Mday)。

本文以Matlab为工具采用粒子群-线性规划算法对该两阶段双层问题进行求解。上层将静态零售定价作为粒子迭代，并依次传入下层作为常量，通过求解各个概率场景的日前调度最优值，获得该粒子下的日前最优调度值概率分布进而求得日前最优调度VaR值，即为粒子的反馈函数值，并以此为依据更新粒子，直至收敛。

算法具体步骤如下：

步骤1：接收现货价格、零售负荷概率分布信息；接收综合能源服务商设备参数；设定服务商置信度α；设置蒙特卡洛法抽样数M，设置聚类典型场景数Nc。

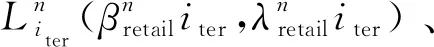
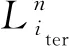
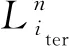
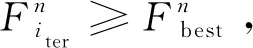
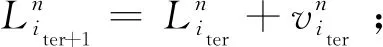
步骤9：重复步骤3—7。

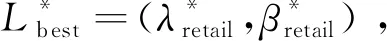
算法流程图如图1和图2所示。

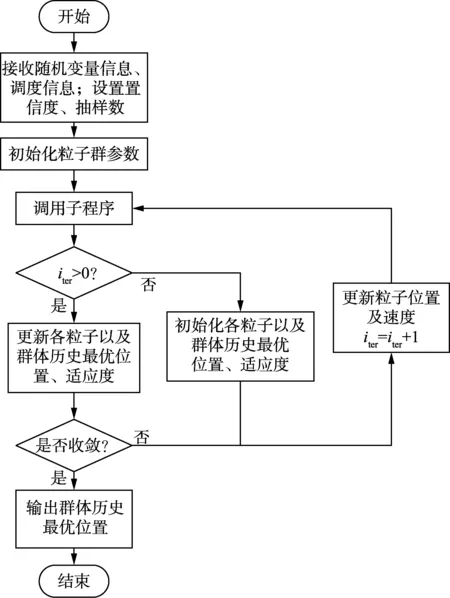
图1 静态零售定价算法流程图Fig.1 Flowchart of static retail pricing algorithm

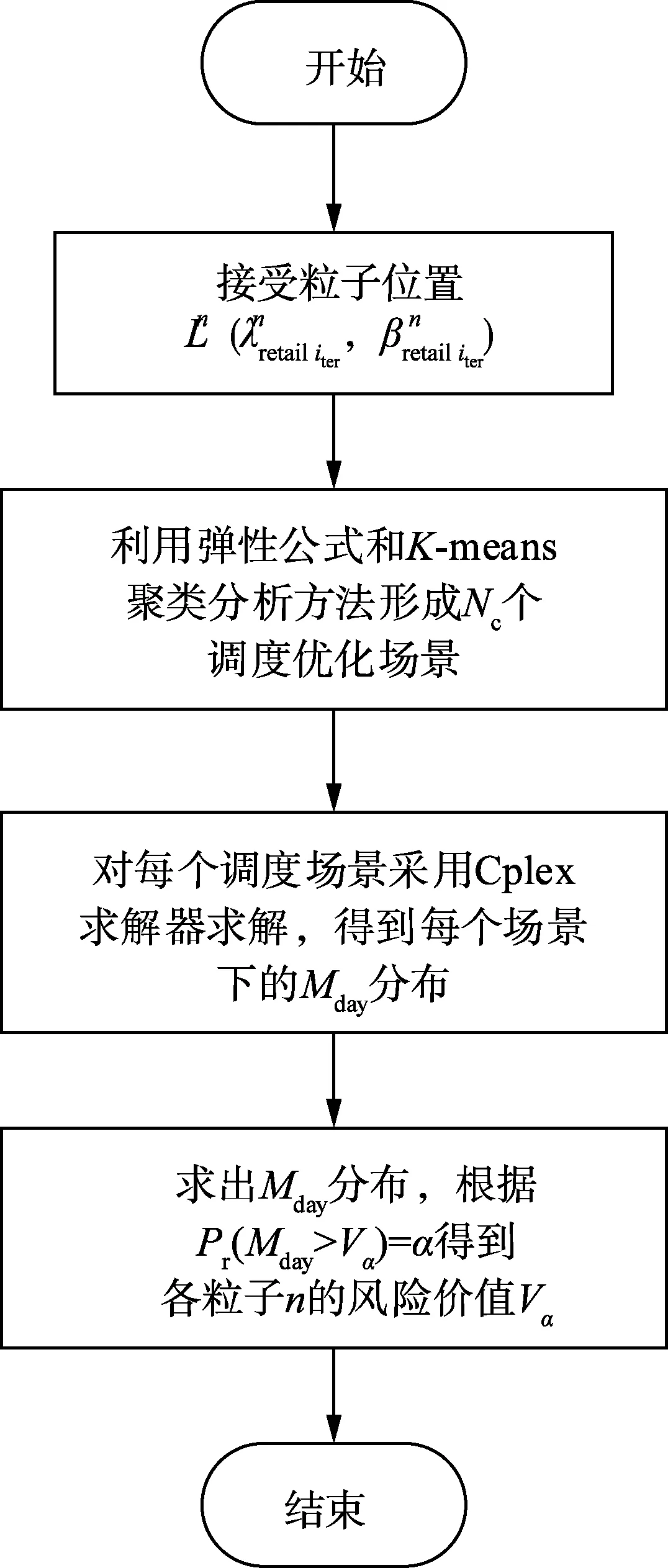
图2 调用子程序的流程图Fig.2 Flow chart of calling a subroutine

3 算例分析

3.1 参数设置

本文算例参数的具体设置如下：抽样次数设置为5 000，场景数设置为Nc=30，置信度α设置为0.9，粒子个数设置为30，惯性系数w为0.3，加速度常数c1、c2均为0.4，最大迭代次数1 000次，收敛判据ε为0.01。

零售电负荷的价格上限为：峰时段1.2元/(kW·h)，平时段0.75元/(kW·h)，谷时段0.55元/(kW·h)；零售热负荷价格上限为0.512元/(kW·h)。零售电负荷弹性参数设置见表1，零售热负荷弹性参数设置见表2，零售电负荷和零售热负荷的概率分布参数见表3。

表1 零售电负荷弹性参数Table 1 Elastic parameters of retail electric load

表2 零售热负荷弹性参数Table 2 Elastic parameters of retail heat load

表3 零售负荷概率分布参数Table 3 Probability distribution parameter of retail load

电力和天然气现货市场的波动方差σλ、σβ分别为1.00和0.07；CHP机组的电效率和热效率分别为0.40和0.45，燃气锅炉的热效率为0.90。该两阶段双层问题在Matlab环境下采用粒子群-线性规划算法求解，求解时间为489.626 333 s，使用电脑处理器为英特尔i7-9700，CPU频率为3 GHz，内存为16 GB。

3.2 结果分析

最优粒子迭代过程如图3所示，经过26轮次外层、780次内层迭代，最优粒子位置收敛，证明所提算法具有较好的收敛性。

图3 最优粒子迭代过程Fig.3 Optimal number of particle iterations

求解所得最优零售静态定价为：零售电价峰时段为0.95元/(kW·h)，平时段为0.70元/(kW·h)，谷时段为0.55元/(kW·h)；热力零售定价为0.45元/(kW·h)。

在最优零售静态定价下，日前调度最优值的概率分布见图4。在置信度为0.9的情况下，其VaR值为4 098.3元，Mday期望值为4 580.5元。从图中可以明显看出，随着置信度的逐渐减少，综合能源服务商的最低收益逐渐升高，但是这也意味着综合能源服务商面临着更大的风险。

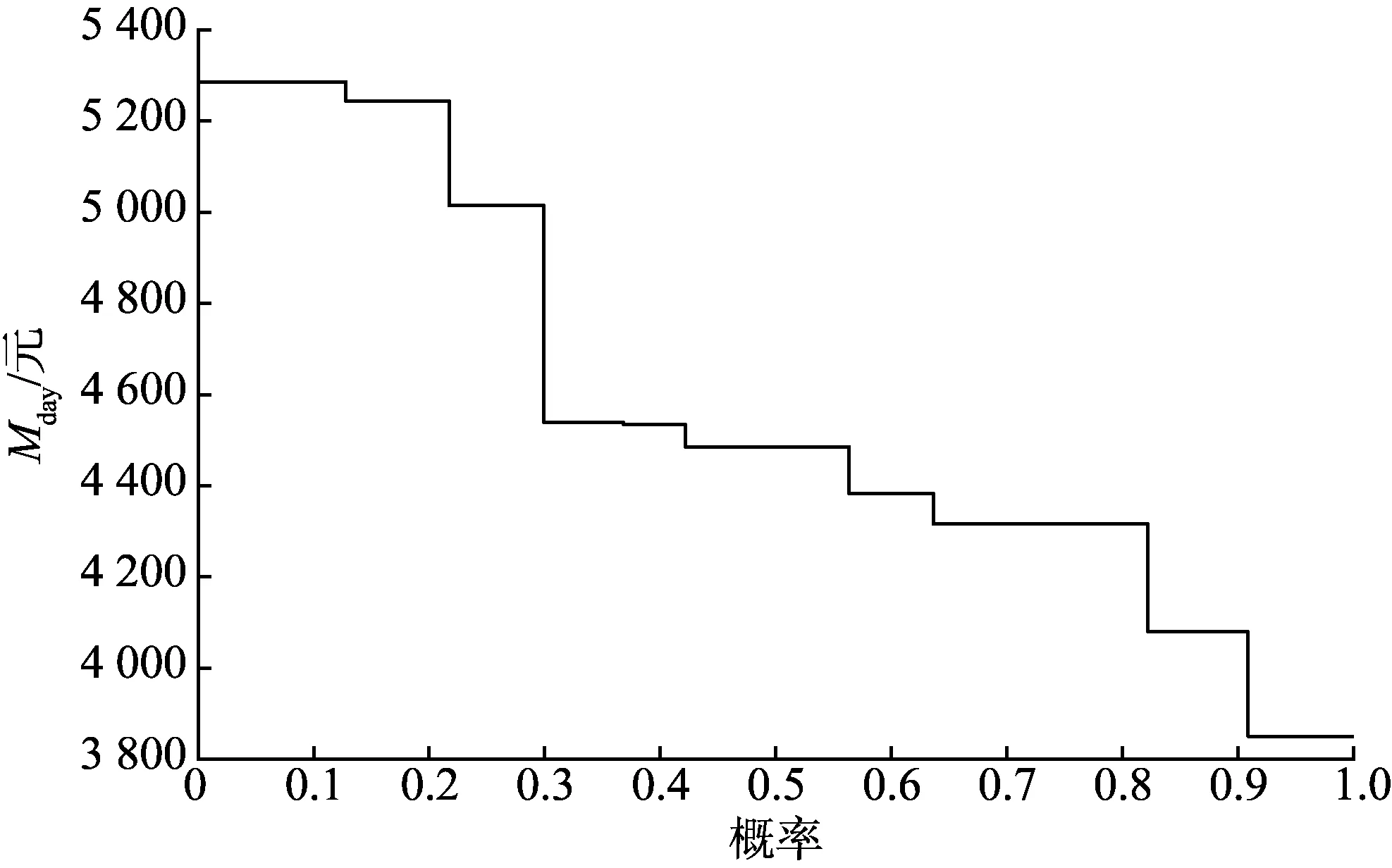
图4 Mday概率分布Fig.4 Probability distribution of Mday

图5为某场景下综合能源服务商的调度情况，由图5可知，一天中现货天然气购买量、CHP天然气消耗量和电力零售负荷都出现了3个峰值，分别是07：00—09：00，12：00—14:00，17:00—22：00，符合正常用户一天的用电习惯。

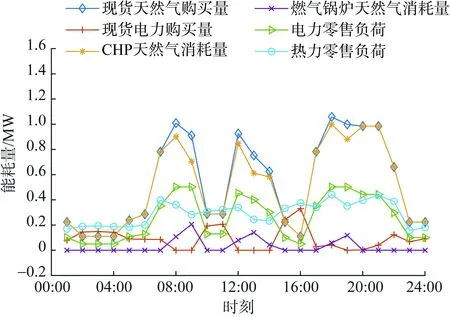
图5 某典型场景日前调度情况Fig.5 Day-ahead scheduling of a typical scenario

在进行粒子群优化之前，本文对4种典型的不确定性因素进行了大量抽样，为了简化优化分析的工作量，采用K-means聚类方法对抽样场景进行典型缩减。

显然，当K-means聚类得到的场景数量越多，优化出的VaR值越准确，但是随着场景数量的增加，计算量与计算时间也会大幅增加。

图6所示为K-means聚类20个场景下的Mday分布图，置信度为0.9时综合能源服务商的VaR收益为4 085.1元，与10个场景下的VaR值的相对误差为0.32%，几乎可以忽略。即K-means聚类出10个场景不仅满足了计算快速的要求，还对误差没有太大影响。

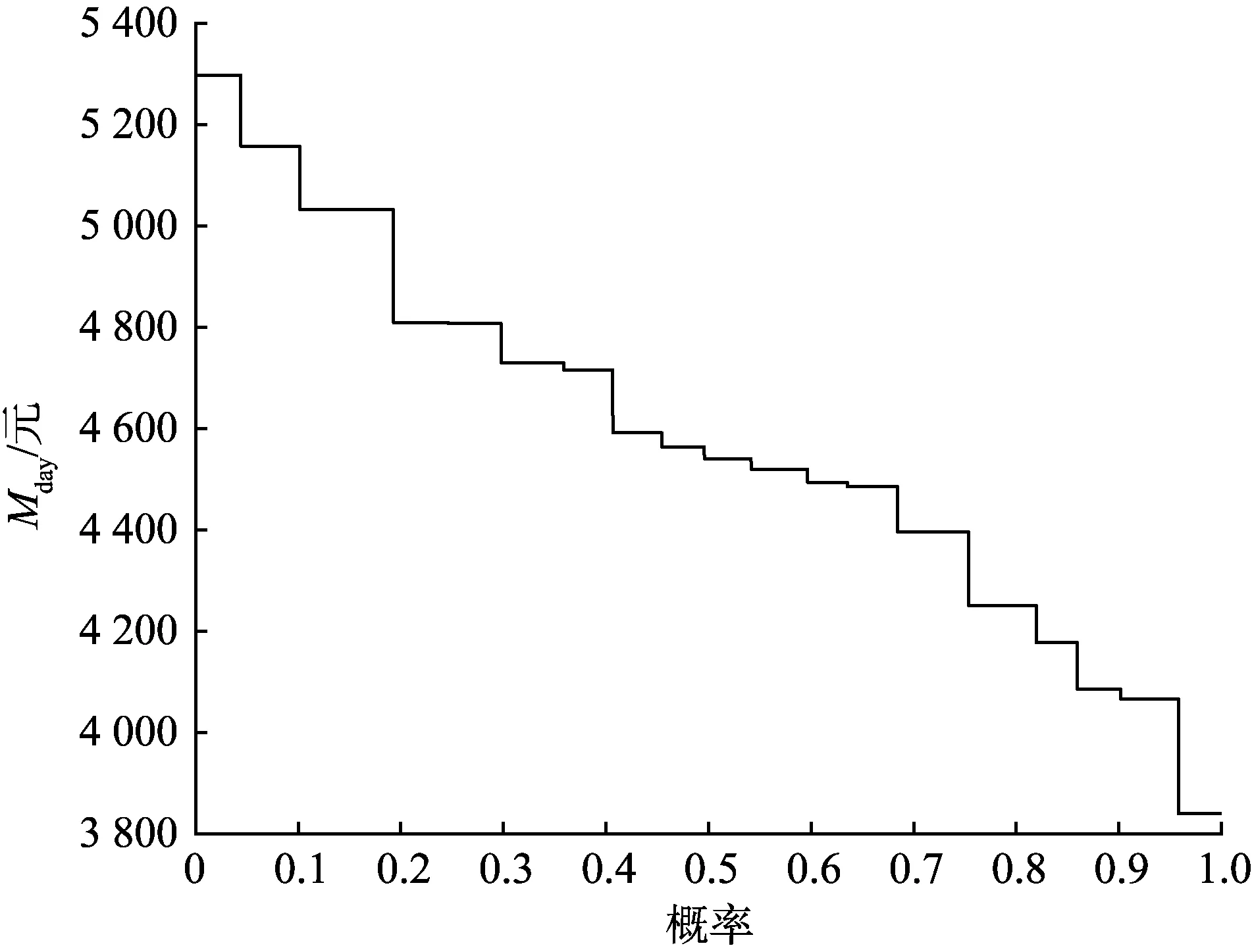
图6 场景数为20时Mday的概率分布Fig.6 Probability distribution of Mday under 20 scenarios

另外，本文选取北京市非居民用电某时期分时电价与热力价格作为对比，峰、谷、平3个时段的电价分别为1.022 7元/(kW·h)、0.874 5元/(kW·h)、0.374 8元/(kW·h)，热力价格为0.55元/(kW·h)。计算综合能源服务商在此价格下10个场景的Mday概率分布，结果见图7，VaR值为869.693 8元，远低于本论文优化方法下的结果。

图7 实际定价情况下Mday的概率分布Fig.7 The probability distribution of Mday under actual pricing

4 结 论

本文建立了综合能源园区零售市场最优策略模型，既考虑了用户对于电能、热能的需求响应，也考虑了用户用能和现货市场能源价格的波动。模型中使用正态分布来体现用户用能以及现货市场价格的不确定性，综合能源服务商在考虑各种不确定后，以自身风险最低为目标，进行能源转换设备的机组组合优化。为了简化问题，模型中使用K-means聚类方法对大量随机情景进行聚类得到典型场景，再使用粒子群算法对零售价格的制定进行优化，算例验证了本文所提模型和方法的有效性，并得出以下结论：

1)基于VaR的零售定价策略优化可以有效降低综合能源服务商的风险，但是同时也会降低综合能源服务商的预期收益，因此选取合适的置信度十分重要，置信度选取过高将无法有效规避风险，置信度选取太低又会降低收益，通常取0.9比较合适。

2)K-means聚类算法将众多随机场景有效地简化成典型场景，结合粒子群优化算法可以在保证精度的前提下有效求解问题。算例表明典型场景选取的多可以增加求解精度，但是将大幅增加求解时间。因此，选取合适的典型场景数量至关重要。

3)本论文提出的考虑需求响应的综合能源园区零售市场最优策略可以显著提高综合能源服务商的收益，为综合能源服务商的能源零售定价提供了模型支撑。