考虑城市不同功能区的电动汽车负荷时空分布建模方法

范磊, 陈良亮，罗雯茜，董晓霄，袁越

(1.国网江苏省电力有限公司，南京市 210016；2.国网江苏省电力有限公司苏州供电分公司, 江苏省苏州市 215004；3.国电南瑞南京控制系统有限公司，南京市 211106；4.南瑞集团有限公司(国网电力科学研究院有限公司)，南京市 211106；5.河海大学能源与电气学院，南京市 211100)

0 引 言

在能源日益紧缺、环境污染问题显著加重的当下，电动汽车(electric vehicle，EV)在节约能源、环境保护等方面具有无可比拟的优势。在可以预见的未来，接入电网的电动汽车负荷必将持续增加。然而，大规模的电动汽车接入将给电力系统的规划与运行带来多种挑战。由于电动汽车充电负荷具有一定的随机性和聚集性，充电负荷接入电网的位置和容量不同，将会给电网带来不同程度的影响[1]。因此，明确电动汽车充电负荷空间分布，对研究电动汽车负荷接入电网的影响具有重要意义。

当前对电动汽车空间分布的移动特性的研究，大多数是通过追踪电动汽车的行车轨迹。传统方法是应用源点-终点(origin-destination, OD)矩阵。但在车辆和路网规模扩大后，OD矩阵维度将急剧增长，难以实现大规模应用，因此多用各种数学模型[2-6]或出行链理论[7-10]得到大区域下的行车轨迹。文献[2]考虑交通网络特征，通过多代理技术得到电动汽车负荷的时空分布。文献[3]与文献[4]利用最短行驶距离算法确定车辆的行驶路径。文献[5]通过聚类分析与历史数据，提出了一种电动汽车时间和能耗最优的路径选择算法。文献[6]利用非齐次马尔科夫模型描述电动汽车的行驶模型。文献[7-9]均以出行链为基础，拟合电动汽车充电负荷的时空特性。文献[10]建立基于随机出行链和马尔可夫决策过程的电动汽车负荷时空模型。由于电动汽车的充电特性与城市各区域的地理位置及职能范围息息相关，而上述文献使用的模型均以电动汽车的出行特性为视角，未从城市的角度进行宏观考虑。

近年来计及城市功能区划分的研究通常只涉及某个具体的场景，例如居民区[11-13]、高速公路快充站[14]等，缺乏对城市内不同功能区的区域特性的综合考虑，导致预测结果具有局限性。重力模型有利于衡量城市范围内路网和土地利用对交通分布的影响，可从城市的角度将不同功能区的特性纳入电动汽车负荷时空分布的考量范围，适用于城市规划清晰、功能类别明确的现代化城市。

基于此，本文提出一种基于改进重力模型的电动汽车负荷时空分布建模方法。首先，对电动汽车进行分类，并根据现有的研究调查结果确定电动汽车的行驶特性，得到电动汽车出行里程分布与充电模式；其次，将城市区域网格化，对城市功能区进行划分，再依据改进的重力模型获取城市各时段各区域的出行矩阵，从而得到电动汽车的时空间分布；最后，结合电动汽车充放电的荷电状态模型，获得电动汽车负荷的时空分布模型。

1 电动汽车行驶特性与荷电状态模型

1.1 电动汽车的出行特性与充电模式分析

车辆的出行特性包括车辆离开起始地的时间、车辆到达终点的时间以及车辆的日行驶里程，这些因素会影响车辆的充电负荷。通过对各类型电动汽车(电动私家车与电动公交车)行驶特性的研究，分析处理可得各类车行驶数据并用于计算。

1)私家车用户行驶特性。2009年美国交通部对美国家庭旅行进行调查研究，最终的统计数据显示[15]，私家车的入网时刻分布、离网时刻分布、行驶里程分布存在一定规律。其中，私家车的单次行程的出行时间及出行起止点与出行矩阵相关(在后文详述)，私家车的日行驶里程服从对数正态分布[7]。

(1)

式中：x代表各时刻；f(x)为概率密度函数；μ是均值；σ是标准差。

电动私家车一般在家、工作地点停留时间较长，在其他区域停留时间较短，因此电动私家车所采用的充电模式由行程终点所在区域决定。若行程终点为居民区、办公区、工厂等，则进行慢充，否则均为快充。

2)公交车用户行驶特性。公交车的出行时间比较规律，一般在06:30 开始出发工作，到23:00结束工作才返回。为保障行程的安全性，一般每日进行2次充电[16]，因此可认为电动公交车在10:00至13:00的换班期间进行1 h的快充，在 23:00至次日06:30的夜间进行慢充。电动公交车的行驶路程相对固定，其日行驶里程满足正态分布，充电场所均为公共设施(充电)区。

1.2 电动汽车的荷电状态模型

以主流的锂电池为例，对单辆电动汽车的充放电特性进行分析。由于锂电池的充电过程以恒功率充电阶段为主，预充电阶段和恒压充电阶段的时间非常短[17]，本文近似认为电动汽车的充放电过程中功率恒定。

电动汽车动力电池的荷电状态(state of charge，SOC)与已行驶距离成反比，随着行驶距离的增加线性下降。

(2)

式中：SSOC,t0为入网时刻t0电池电量c与电池容量cmax的比值,即为入网时刻电池SOC；d为上次充电后已行驶的路程；dm为电动汽车的标准续航里程。

单辆电动汽车接入充电桩后，首先判断是否需要充电。若电动汽车行驶终点为居民区，则开始进行慢速充电；若行驶终点为其他区域且电量在60%以上，则无需充电。若需充电，其充电需求S与入网时刻电池荷电状态SSOC,t0、电池容量cmax的关系可以表示为：

S=(1-SSOC,t0)cmax

(3)

电池t时刻的SOC值SSOC,t与充放电功率P、充放电效率η的关系可以表示为式(4)，其中充放电功率P由所采用的充电模式(快充/慢充)决定。

(4)

为满足车主的出行需要，认为电动汽车每次充电均充满。由于电动汽车的充放电过程中功率恒定，因此充电时长ts可以由下式表示：

(5)

2 基于改进重力模型的电动汽车时空分布模型

电动汽车一般在停泊位置进行充电，因此电动汽车负荷的时空分布与各地区各时刻的流量息息相关。本文综合考虑不同城市功能区的特性、路网和土地利用以及交通阻抗对交通分布的影响，依据改进的重力模型对电动汽车的空间分布进行预测。

2.1 城市功能区划分

城市用地类型主要包括居住用地、公共设施用地、工业用地、仓储用地、对外交通用地、道路广场用地、市政公用设施用地等。本文主要对预测城市进行商业区、居民区、工业区、办公区、公共设施区、公园的划分，具体分为不同的交通区。

引入出行矩阵来描绘各交通区各时刻的到达率(以该区域为终点的概率)。设定该交通区的出行矩阵为：

(6)

2.2 传统重力模型

重力模型又称引力模型，由Casey提出，它考虑了交通阻抗对出行分布的影响。传统重力模型主要有简单重力模型法、单约束重力模型法和双约束重力模型法。重力模型法的优点在于直观且容易理解，并考虑了路网和土地利用对交通分布的影响，对基年出行量为0的地区也可以进行估算。

根据重力模型，交通区i、j之间的出行量与交通区i的产生量和交通区j的吸引量的乘积成正比，与交通区i、j之间的交通阻抗成反比。其基本公式如下：

(7)

式中：βij为交通区i、j之间的出行量；α为调整系数；Zi为交通区i的交通产生量；Qj为交通区j的交通吸引量；Fij为交通区i、j之间的交通阻抗。

2.3 基于改进重力模型的出行矩阵计算

各交通区的到达率与该交通区的特性相关，并满足重力模型思想，即与各交通区之间的交通出行量成正比关系，与交通阻抗成反比关系。而传统重力模型的缺点在于其采用集计模型分析交通出行，其道路交通阻抗、交通产生量、交通吸引量均为恒定不变的，无法针对一天中的不同时段进行动态分析，由此造成与实际情况存在一定的偏差。因此，本文设置随时间变化的交通区出行力与地区吸引力参数，以此替代传统重力模型中的交通区的交通产生量和交通吸引量，从而规避传统重力模型参数为静态的缺点，建模思想如图1所示。

图1 电动汽车出行分布预测建模思想Fig.1 Modelling idea of EV travel distribution prediction

首先根据土地使用情况，将城市进行功能区划分，再根据地理位置划分为不同交通区，由出行起止点所属区域确定出发地的出行力与到达地的吸引力。其次，由两地之间的距离确定出行阻抗函数，代入改进的重力模型函数即可求取电动汽车出行矩阵。具体步骤如下：

电动汽车行驶里程分布满足对数正态分布，地区之间的阻抗由两地之间的距离决定，因此各交通区之间的交通阻抗Fij用式(8)表述：

(8)

式中：f2(·)为概率密度函数；μ2是均值；σ2是标准差；lij为交通区i到交通区j的距离。本文中μ2=2.78，σ2=0.82。

(9)

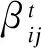
(10)

由式(10)可以计算出待定的调整系数θt的值。

(11)

2.4 充电负荷计算及仿真流程

根据上述理论分析，设计电动汽车充电负荷预测的仿真流程，如图2所示。

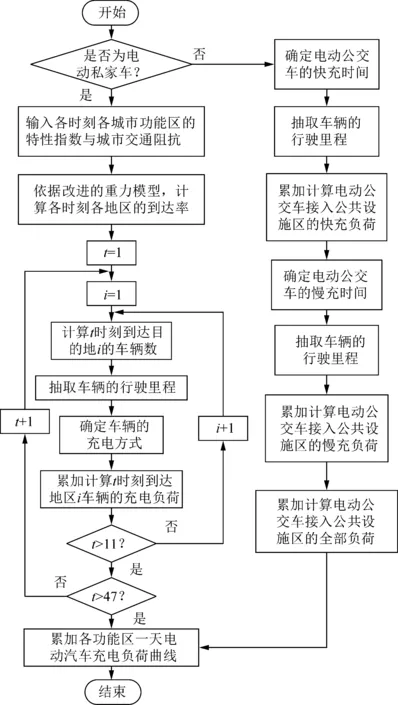
图2 电动汽车充电负荷预测流程图Fig.2 Flow chart of EV charging load prediction

本文将城市分为N个交通区，将一天分为48个时段(每个时段为0.5 h)，并将电动汽车分为电动私家车与电动公交车进行分析计算。电动公交车的出行路径、充电方式、充电时间地点固定，抽取车辆的出行里程，结合车辆的荷电状态模型，即可求出当日的充电负荷曲线。电动私家车的出行矩阵则由各时段各类区域的特性指数(地区出行力与地区吸引力)确定。区域的特性指数由该区域所属的城市功能区的类别决定，是随时间变化的已知量，根据滴滴大数据平台(https://gaia.didichuxing.com)提供的出行数据统计分析得到[18]。由出行矩阵确定该城市t时刻到达目的地的汽车数量Vt，由式(3)抽取该时段每个车辆的日行驶里程以确定该车辆入网的初始SOC，根据t时刻各个区域的出行矩阵确定每个车辆的入网位置，结合式(4)—(8)计算出t时刻的充电负荷时空分布。

3 算例分析

3.1 算例参数

本文以A市作为对象进行研究，该城市区域模型构架以文献[19]中的算例模型作为样本。A市的用地规划如图3所示，共分为6个功能区类别、A1至A12共12个区域。

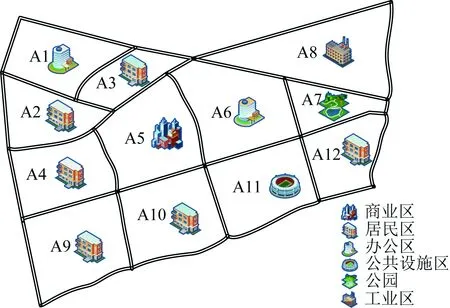
图3 A市的功能区划分Fig.3 The urban functional area division of city A

表1展现了A市各区域编号所对应的类别，能够更为直观地对各区域的类别进行一一对应。

表1 A市各区域所属的城市功能区名称Table 1 Names of the urban functional area of each region in city A

假设A市日均产生10 000条电动私家车上路行程和200条电动公交车上路行程。将一天24 h分为48个时段，每个时段为0.5 h，第一个时段结束时刻为当日00:30，最后一个时段结束时刻为第二日00:00。

A市各地区之间的距离指各个地区地理中心点之间的距离，具体数值见附录表A1。根据各地区之间的距离，代入式(8)，可计算出各地区之间的阻抗Fij，具体数值见附录表A2。阻抗函数可衡量各区域之间市民的出行意愿，两地之间的数值越高，则表示两地市民往来的交通流量越小，阻抗函数分布如图4所示。

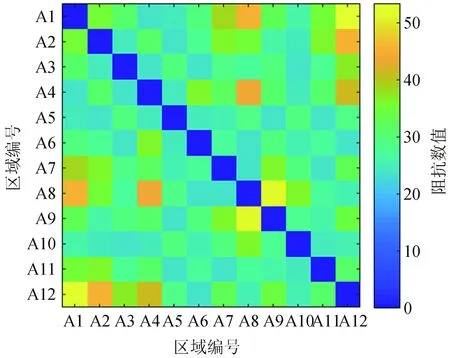
图4 A市的各区域之间的阻抗函数Fig.4 The travel intention between different regions in city A

需要特别说明的是，地区出行力及地区吸引力由各地区的类型特性决定，且随时间动态变化，具体数值如附录图A1与A2所示。

由于电动汽车的型号与类型种类繁多，根据实际情况，本文分别参考比亚迪E6型电动汽车与比亚迪K9型电动公交车的车辆参数[16]，设置A市的电动汽车电池参数均值，如表2所示。

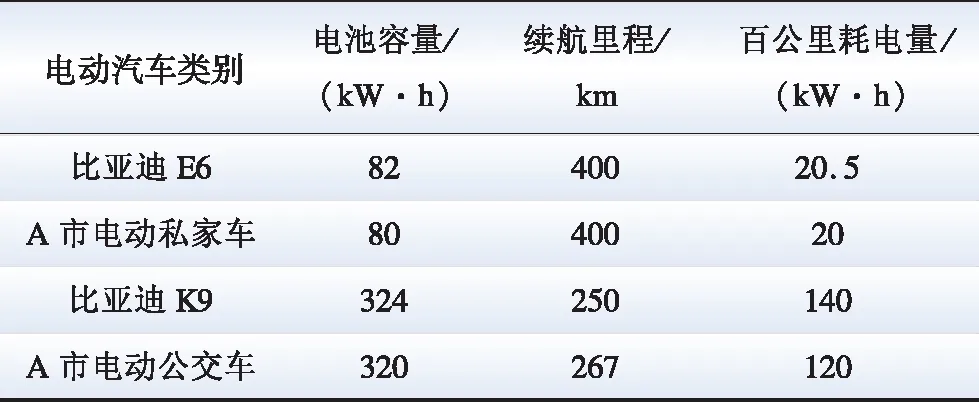
表2 电动汽车的参数Table 2 Parameters of electric vehicles

如式(1)所示，电动汽车的行驶里程呈对数正态分布，选取μ=2.78，σ=0.82。一日内电动公交车的行驶里程呈正态分布，选取均值为100 km。

考虑适用性与普遍性，本文采取锂电池进行充电模式建模。电动汽车的充电模式主要有常规模式、快速充电模式和更换电池模式。结合实际情况，本文电动私家车在到达地点为居民区、办公区、工厂时进行慢充，其余地区则进行快充；电动公交车在10:00至13:00的换班期间进行1 h的快充，在 23:00至次日06:30的夜间进行慢充。锂电池的充电过程具有近似恒功率特性，因此将充电功率P视为常数，在慢充情况下充电功率为8 kW，在快充情况下充电功率为60 kW[20]。由于锂电池具有能量密度大、自放电小等优点，其充电效率通常可达到95%及以上，为方便计算，本文取充电效率η为100%。

3.2 电动私家车负荷的时空分布建模结果

A市各时段入网电动汽车的行驶里程分布如图5所示。由图5可知，在城区内市民的行驶里程基本在30 km以内，大部分车主选择在早晨出发与傍晚结束行程，出行高峰出现在清晨上班与傍晚下班返程这2个时段，符合人们的日常作息习惯。

图5 各时刻入网电动汽车行驶里程分布Fig.5 Distance distribution of EVs integrated into power gird at each moment

本文首先选取同一功能区类别但坐落在不同位置的区域进行横向对比。A市居民区各时刻的充电功率如图6所示。通过对比得知，各区域的充电功率变化趋势大致相同，但数值略有差异。由于所处的空间位置不同，A2、A4、A9、A12地区的充电功率比A3与A10更低。相较于其他居民区，A3与A10的位置更为中心，道路阻抗更小，因此更容易被选为出行终点。

图6 各时刻居民区的充电功率Fig.6 Charging power of different regions of residential areas at each moment

此外，本文将传统重力模型与改进重力模型的充电功率仿真结果进行对比，如图7所示。

图7(a)中各区域的充电功率变化趋势一致，仅有数值大小上的差异，表明传统重力模型不能很好地描述一天中各功能区充电功率的动态特性，仿真结果不准确。图7(b)中改进的重力模型可刻画不同类别的城市功能区之间充电功率曲线的动态差异：工业区与办公区充电功率峰值时段大致相似，均为上午上班时刻，公园与公共设施区充电负荷主要集中在午后及傍晚的休闲时段，商业区在午休及夜间时段迎来充电高峰，居民区的充电负荷主要集中在傍晚至夜晚的返家时段。

3.3 不同场景下仿真结果的对比分析

为进一步验证所提模型的准确性与普遍适用性，本文设置以下3种场景进行对比分析。

场景1：加入电动公交车的城市充电负荷。除电动私家车外，电动公交车由于其噪音小、行驶平稳、无排放等特性，被逐步运用在了各大城市的公共交通上。

由于电动公交车充电地点唯一，为公共设施区下属的公共充电区，因此本文对比加入公交车负荷前后的公共设施区的充电功率，分析结果如8所示。

由图8可以看出，在中午换班前后的快充阶段，电动公交车接入电网的充电负荷较大，易对电网产生较大的冲击。

图8 公共服务区有无电动公交车的充电功率Fig.8 Charging power of public service area with or without the charging power of electric buses

场景2：城市商业区扩建后的充电负荷。近年来，人们外出购物、品尝美食、观看电影等一系列娱乐活动的需求不断增多，原有商业区的规模可能无法满足人们的需求，因此将城市商业区覆盖范围进行扩大。本文分别对比商业区扩建前后城市的商业区与公共设施区的充电功率，分析结果如9所示。

由图9可得，在商业区扩建后，商业区自身的充电功率曲线趋势与未扩建时的大体一致，但充电功率数值有了较大的增长。扩建后的商业区服务设施更加完善，能同时容纳更多市民。由于商业区(A5)与公共设施区(A11)距离较近，扩建后的商业区带动了周边的公共设施区，因此该区的充电功率数值也有了一定的提升。与此同时，居民区充电功率曲线有了一定程度的时延，在商业区扩建后娱乐项目增多的情况下，部分市民返家的时间有所延后。

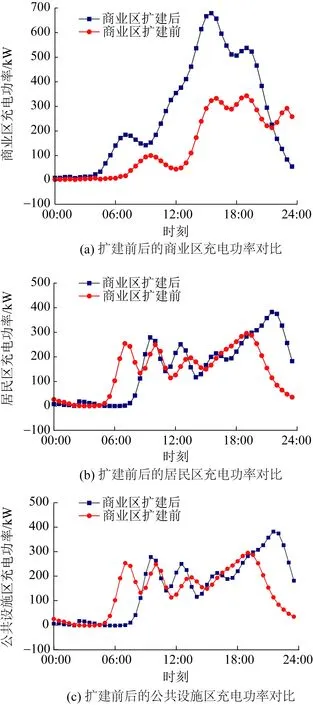
图9 城市商业区扩建前后城市的充电功率Fig.9 Charging power of the city with or without the expansion of urban business district

场景3：市民办公时长增加后的充电负荷。在年底等工作量增加的时段，市民的工作时间可能延长。现将A市市民的上班时间提前、下班时间往后顺延，市民办公时间增加前后的充电功率对比如图10所示。

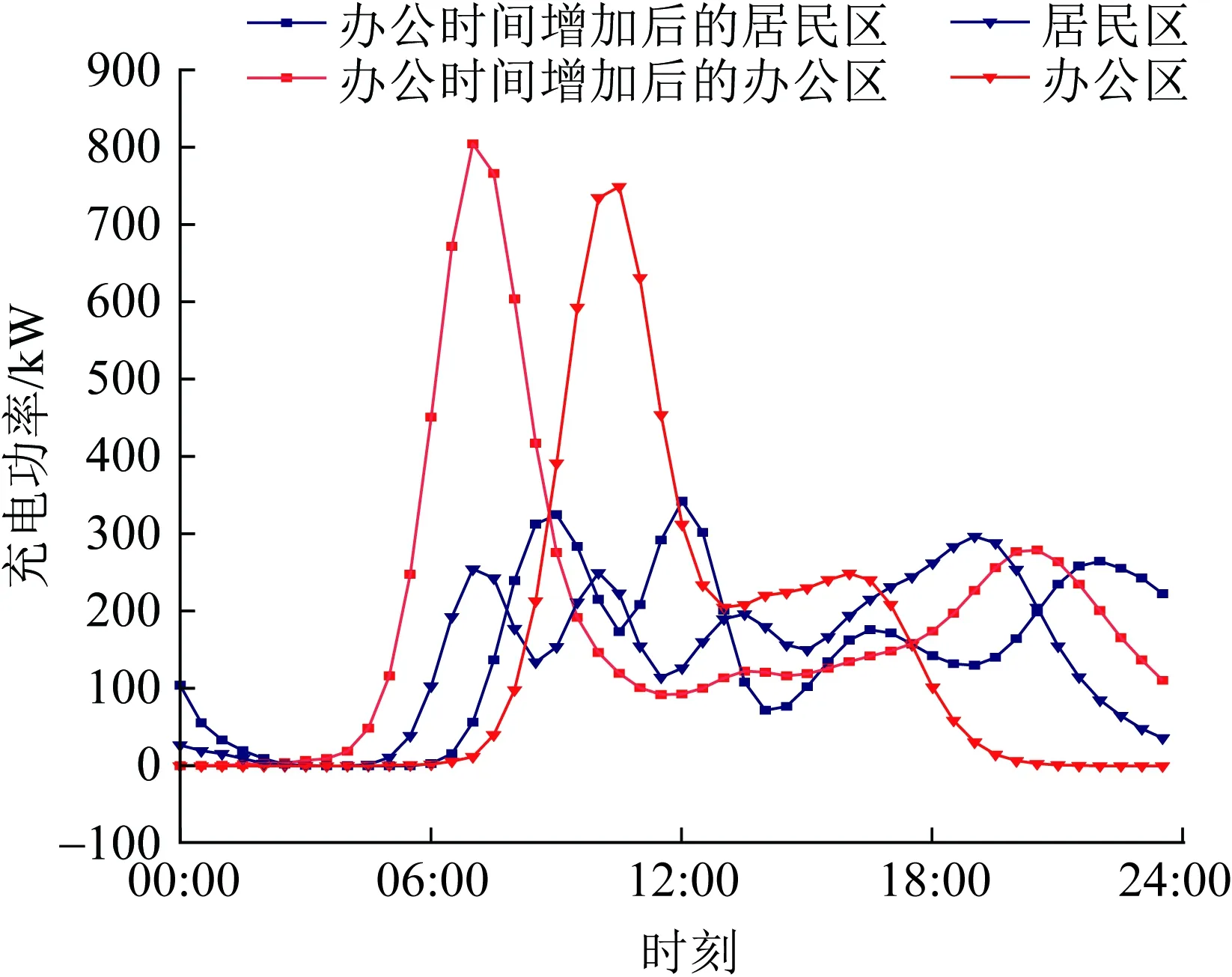
图10 办公时间增加前后城市的充电功率Fig.10 Charging power of the city with or without the increase of working hours

在市民办公时长增加后，早间时段办公区的充电负荷峰值前移，晚间时段充电负荷峰值后移，同时居民区充电功率峰值后移且数值略微下降。在工作时长增加后，选择在办公区进行充电的车主增多，且返家的时间明显后延。

4 结 论

本文依据重力模型思想，考虑了不同城市功能区的特性以及电动汽车的种类与充电方式，对电动汽车负荷时空分布进行了研究。本文提出的方法规避了传统重力模型仅采用静态参数的缺点，地区产生力和地区吸引力不再是一成不变的参数，其数值随着各个时刻动态变化。分析结果表明，不同类别的城市功能区之间负荷分布差异较大且与各区域吸引力相关；属于同一类别但处于不同地理位置的地区之间的负荷分布也略有差异，位于城市中心地区的负荷较高。在城市功能区扩建、市民生活节奏改变后，各地区的功率曲线将发生相应变化。

依据本文算例的结果，可进行换电站的规划、交通规划、电网规划以及运行调度控制的影响等后续研究。有助于电动汽车作为虚拟储能在城区内进行合理调度，从而达到削峰填谷、消纳可再生能源的目的。此外，本文在仿真中忽略了一些影响因素，例如电池使用的损耗、真实路况对耗电量的影响，驾驶员主观行为等，后续可针对以上因素对各地区进行更为精细化的研究。