智能变电站中网络对时的优化设计

朱超， 邓凯， 张海华， 谭风雷， 吴兴泉， 徐刚

(国网江苏省电力有限公司检修分公司，江苏 南京 211102)

0 引 言

随着通信和自动化技术的不断发展，智能变电站取代常规变电站已逐渐成为一种技术趋势[1]。广域信息同步实时采集技术是实现智能变电站各项应用功能的基础，它要求电子式互感器对电网电流和电压的数据一经采样便可被多个智能变电站中各个智能电子设备(intelligent electronic device，IED)共享。然而，无论控制和保护[2-3]，还是监测和计量的计算处理都要求采样数据应在同一个时间点上采集，以免相位和幅值产生误差[4-7]。智能变电站中IEEE 1588(IEC 61588)网络对时信息与采样值共网传输时，由于IEEE 1588对时信息网络传输的往返延时不一致，从而造成同步精度降低。本文通过构建多次对时信息交换的时钟模型，并对本地时钟相偏进行最优推导，显著减小了网络传输延时不对称对智能电子设备的对时影响[8-9]。

1 本地时钟相偏计算方案

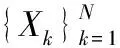
PTP协议单次对时信息交换中跟随信息包与延时测量应答信息包主要是为了让本地时钟获得主时钟精确的发送和接收时间。不考虑本地时钟频偏的影响，PTP协议多次对时信息交换的时钟模型如图1所示。

图1 多次对时信息交换的时钟模型

图1中:实际发送时间T1,N，本地时钟记录信息包的到达时间T2,N，随后在T3,N时刻发送延时请求信息包；主时钟记录延时请求信息包的到达时间为T4,N。由于主时钟与本地时钟之间的信息交换延时不对称，共需要N次对时信息交换来对本地时钟相偏Φ进行数理统计估算，N为统计计算所需样本数。在PTP对时协议中，通过硬件打时标法，上层处理延时可忽略不计；第k次信息交换中，信息由主时钟到本地时钟的网络传输延时设为随机变量Xk，信息由本地时钟到主时钟的网络传输延时设为随机变量Yk。因此，信息包时标T1,k、T2,k、T3,k和T4,k之间关系可表示为：

T2,k=T1,k+d+Φ+Xk

(1)

T4,k=T3,k+d-Φ+Yk

(2)

式中:d为物理层处理延时设定值。在第k次的对时信息交换中，本地时钟与主时钟之间对时信息交换的往返延时Uk及Vk可定义为：

Uk=T2,k-T1,k=d+Φ+Xk

(3)

Vk=T4,k-T3,k=d-Φ+Yk

(4)

因此若直接通过式(2)进行计算，得到本地时钟与主时钟的时钟相位偏移Toffset为：

(5)

可看出由于网络传输延时不对称的影响，其误差分量(Xk-Yk)/2将会直接影响PTP对时协议中对本地时钟相偏Φ的计算。当网络传输往返延时的时间差达到2 μs时，便不能满足采样值计量需要的T5精度等级要求。

通过极大化似然函数可以得到参变量的极大似然估计值[11]。在区间范围{(d,Φ)|d>0,-∞<Φ<﹢∞}内，得出物理层处理延时定值最大似然值dMLE，本地时钟相偏值最大似然值ΦMLE分别为：

(6)

式中:U(1)及V(1)为首次信息交换往返延时值。相偏计算的极大似然估计方法主要在网络传输延时对称性较好的情况下进行推导。因此在网络传输延时不对称性较为严重时，得到的估计值是次优的，无法满足实际网络对时的需要。

当网络传输中背景流量较大时，网络传输延时变大、随机性增加，此时网络传输的往返延时Xk与Yk是不对称的，有网络传输的往返平均延时α≠β。因此，可运用顺序统计的最优线性无偏估计对本地时钟相偏进行推导计算，最优线性无偏估计δ′为：

(7)

2 本地时钟相偏的最优估计

将式(6)极大似然估计、式(7)线性无偏估计值进行均方误差计算，得出两种均方误差值MSE(ΦMLE)及MSE(Φ′)分别为：

(8)

由于四种对时信息包的长度平均为70 Byte，其最佳情况下网络延时为17.6 μs，因此考虑网络传输接收延时β为18 μs时，在不同对时信息包交换次数N与不同网络传输发送延时α下，极大似然估计均方误差MSE(ΦMLE)与线性无偏估计MSE(Φ′)的曲面图如图2所示。从图2可以看出：当N=10时，极大似然估计在取12～28 μs范围内优于线性无偏估计；当N=20时，极大似然估计在α取14～23 μs范围内优于线性无偏估计。因此随着N的增大，极大似然估计的最优范围逐渐缩小，最终只要N足够大，线性无偏估计将恒优于极大似然估计。但在实际计算中，计算量有限，同时观察到图2中网络传输延时不对称性较为严重，当α为50 μs时，若N取值小于等于10，则线性无偏估计的均方误差将大于3 μs，误差较大。同时随着N取值变大，均方误差迅速减小，在N值大于等于16以后，线性无偏估计的均方误差将小于2 μs，且均方误差下降较为平缓，此时即使增大N值，对于减小均方误差效果也不是很明显。因此，本文在综合考虑下取N为16。

图2 相偏估计的均方误差曲面图

通过式(8)可以看出，尽管本地时钟相偏的极大似然估计在网络传输延时不对称情况下进行的相偏估计是有偏的，但在一定条件下它比线性无偏估计有更好的性能。

MSE(ΦMLE)>MSE(Φ′)

(9)

(10)

由上式关系可以看出，当对时信息包的交换次数N一定，即相偏计算所需的样本个数一定时，对于网络传输的往返平均延时α和β，其延时越大且不对称程度|α-β|越小，极大似然估计将比线性无偏估计具有更小的均方误差。当网络传输延时只是轻微的不对称时，在α=β附近，极大似然估计具有更好的估计效果。但当网络传输延时不对称性逐渐增加，|α-β|逐渐偏离0时，线性无偏估计逐渐优于极大似然估计。

当对时信息包交换次数N为16、网络传输接收延时β为18 μs时，网络传输发送延时α在0到50 μs之间变化时，极大似然估计MSE(ΦMLE)、线性无偏估计MSE(Φ′)与PTP协议原始算法[12]的均方误差曲线如图3所示。PTP协议原始算法的相偏估计只针对网络传输的往返延时相等时有效，当网络传输往返延时不对称时，误差迅速增大。同时网络传输发送延时α在34 μs以内变化时，采用优化算法可保证计算误差在1 μs以内，保证采样值计量的T5等级要求。

图3 相偏估计的均方误差曲线

因此为实现相偏计算最优估计，需要根据网络延时进行自适应选择。如图4所示，首先通过式(9)对网络传输延时α和β进行估算，然后将其代入式(10)，检验不等式成立与否。若不等式成立，则选取极大似然估计进行相偏计算，若不等式不成立，则选用线性无偏估计进行相偏计算。

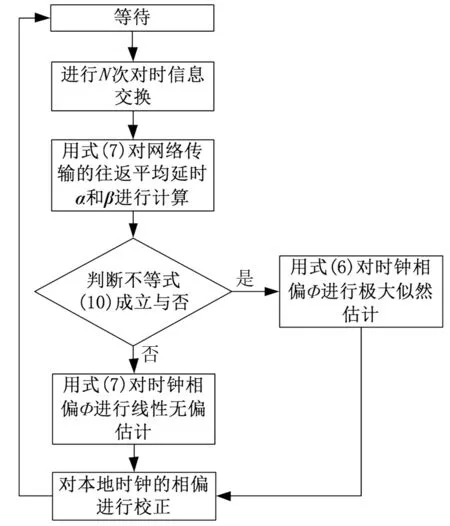
图4 本地时钟相偏计算流程图

3 试验验证

为验证方法有效性，如图5所示，按照IEEE 1588协议采用MATLAB搭建同步仿真模型。对比方法为IEEE 1588方法。试验按照典型变电站级联拓扑搭建端到端仿真试验网络，主从时钟端到端路径包含主时钟到交换机1、交换机1到交换机2和交换机2到从时钟智能组件3段子路径。

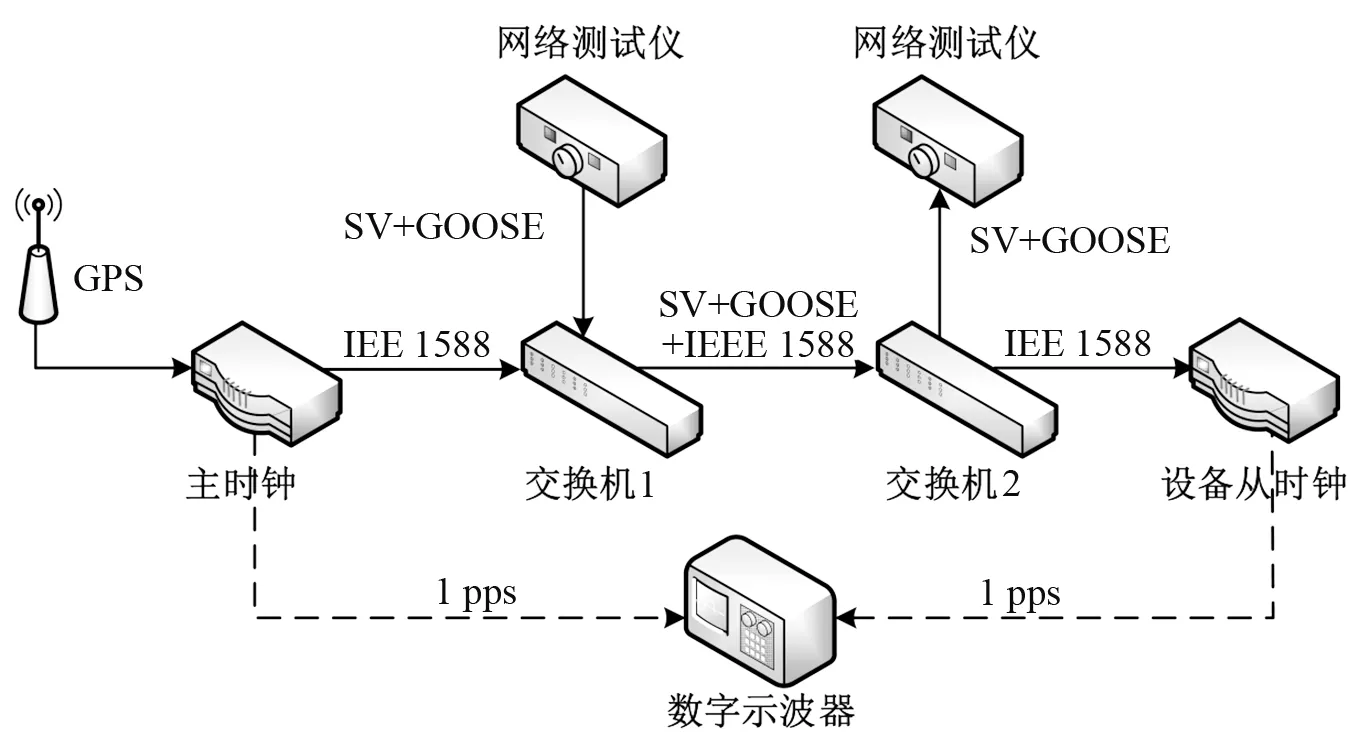
图5 同步时钟测试平台

仿真时间为4 500 ms，统计时间间隔为1 μs；同步周期设为20 ms，每秒由时钟频率偏差造成的误差为25 μs；参考同步时间试验参数典型值，设主从时钟间通信的基础时延为51 μs，每段子路径为17 μs；子路径时延抖动范围为[0,1]μs。

对[500,4 500]ms时间区内从时钟偏差进行统计，从时钟采用IEEE 1588和本文方法的时间偏差变化曲线如图6所示，统计结果如表1所示。

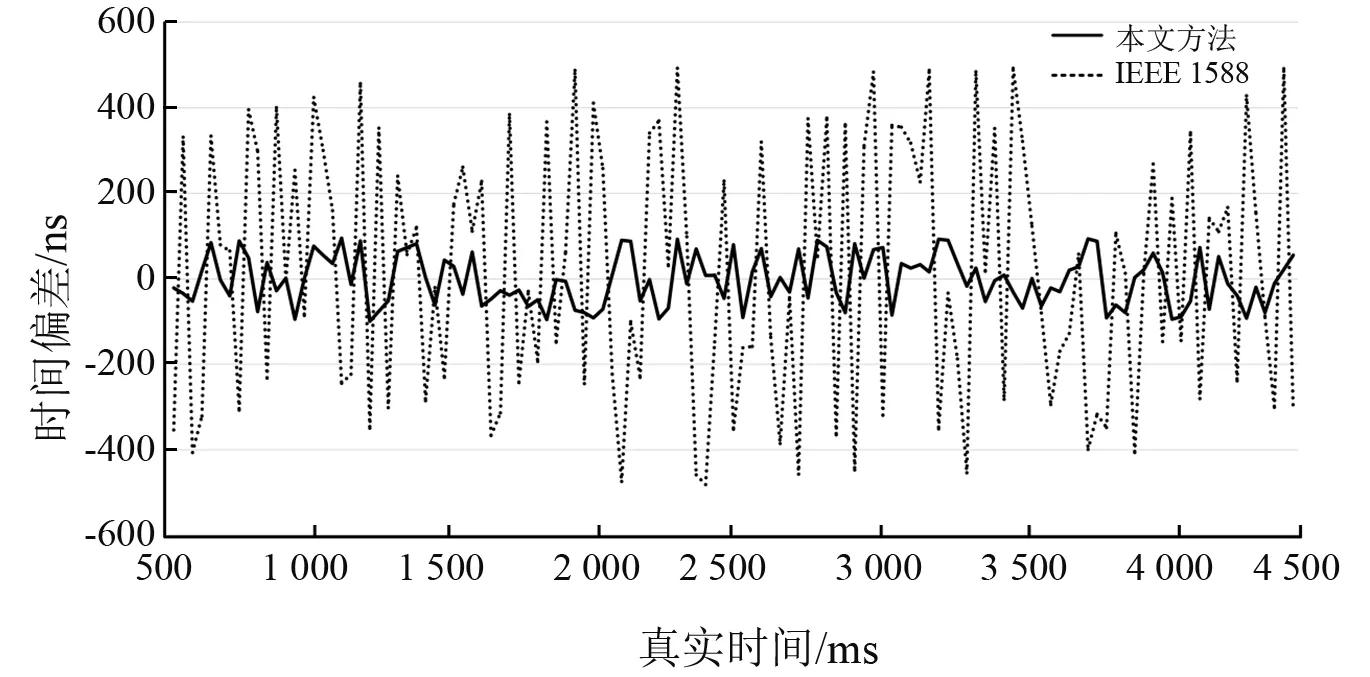
图6 从时钟偏差对比图

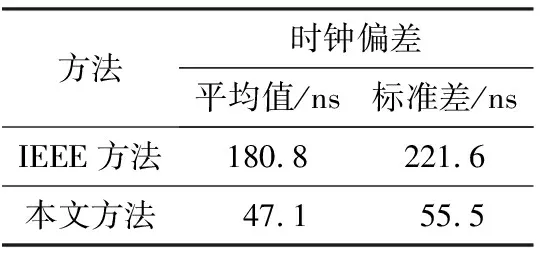
表1 从时钟偏差统计数据

由表1可知本文方法的平均偏差仅为IEEE 1588方法的26.05%，标准差仅为IEEE 1588方法的25.05%。因此针对数据传输往返延时对称的微小抖动，本方法通过计算网络传输延时后，针对微小抖动，采用极大似然估计方法进行计算，能够减小延时抖动对时钟同步的影响，同步性能准确性和稳定性优于IEEE 1588方法。

针对智能变电站中SV、GOOSE、IEEE 1588报文共网传输时，尤其是SV报文要求全站同时采集发送，容易引起三种报文中传输优先级最低的IEEE 1588报文产生网络传输堵塞，造成交换机网络传输延时增加，使得对时数据传输延时产生较大抖动，影响对时精度[13]。对此，仿真模型在第1 500 ms和3 000 ms分别引入不平衡传输延时，得到仿真结果如图7和表2所示。

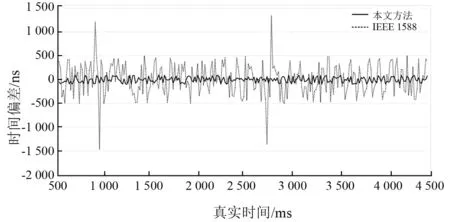
图7 从时钟偏差对比

由表2可知，在1 500 ms和3 000 ms产生网络堵塞时，本文方法对数据传输往返延时进行计算，判断出网络传输延时异常，自动切换采用线性无偏估计对延时进行补偿计算，可以将误差控制在100 ns以内，显著优于IEEE 1588对时方法。

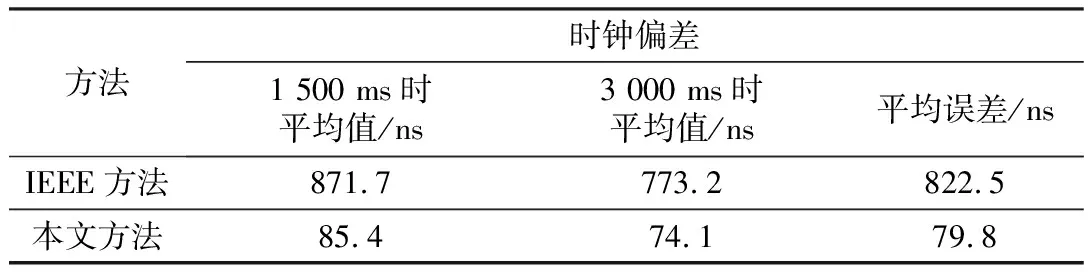
表2 从时钟偏差

4 结束语

同步采样时钟是实现智能变电站过程层采样值站内同步和站间同步的重要时标参考源。本文针对智能变电站中IEEE 1588对时信息与采样值共网传输时，由于IEEE 1588对时信息网络传输的往返延时不一致，从而造成同步精度降低的问题。通过构建多次对时信息交换的时钟模型，并在该模型下基于极大似然估计与最优线性无偏估计，得到了本地时钟相偏的最优计算方法。同时对频偏的极大似然估计算法进行了优化，提出了本地时钟频偏和相偏的联合估计方法，减小了网络传输延时不对称对IEEE 1588网络对时精度的影响，为智能变电站实现广域信息同步实时采集奠定了基础。