正则化与ELM结合用于光伏发电功率预测
李正刚, 王智方, 钟建伟, 张钦惠, 程明亮
(1.国网湖北省电力有限公司巴东县供电公司,湖北 巴东 445000;2.湖北民族大学 信息工程学院,湖北 恩施 445000)
0 引 言
传统化石能源在枯竭,可再生能源进入人们的视线[1]。太阳能是较好的替代能源[2],人们越来越关注光伏发电预测[3]。光伏发电受制于太阳辐射和天气因素[4],影响了电网的运行和调度[5]。
ELM在回归分析、分类和预测领域都有极快的学习速度[6]。该算法还可以降低陷入局部最优的可能性[7]。正则化通过约束最小化经验误差函数来解决逆问题的不适定性,改善用于求解数据的精度[8]。
本文提出一种使用正则化方法优化ELM数据精度的预测方法。引入正则化项改进ELM的泛化能力,避免过拟合,改善用于求解的数据的精度,提高预测的精度。采用DKA太阳能中心的实际数据以验证预测方法提高光伏发电预测精度的能力。
1 正则化理论
正则化理论(regularization theory)在数值分析分析领域应用较多,稳定有效是该理论的特点。正则化方法包括截断奇异值分解(truncated singular value decomposition,TSVD)方法和其他一些改进的算法。
TSVD方法以奇异值展开为基础,k核的平均收敛展开式为:
(1)
式中:ui和vi为正交函数序列,且所有的μi≥0。其解为:
(2)
式中:(ui,g)为内积。只有当系数(ui,g)比ui更快地衰减到零时,解f才能存在。
(3)
这就是著名的皮卡德条件。
2 ELM算法
极限学习机(ELM)算法的目的就是解决基于梯度算法收敛慢和存在局部极小值等相关的问题,该算法是一种单隐层前馈神经网络学习算法。ELM的学习速度非常快。在大多数情况下,ELM在泛化能力方面优于基于梯度的学习。
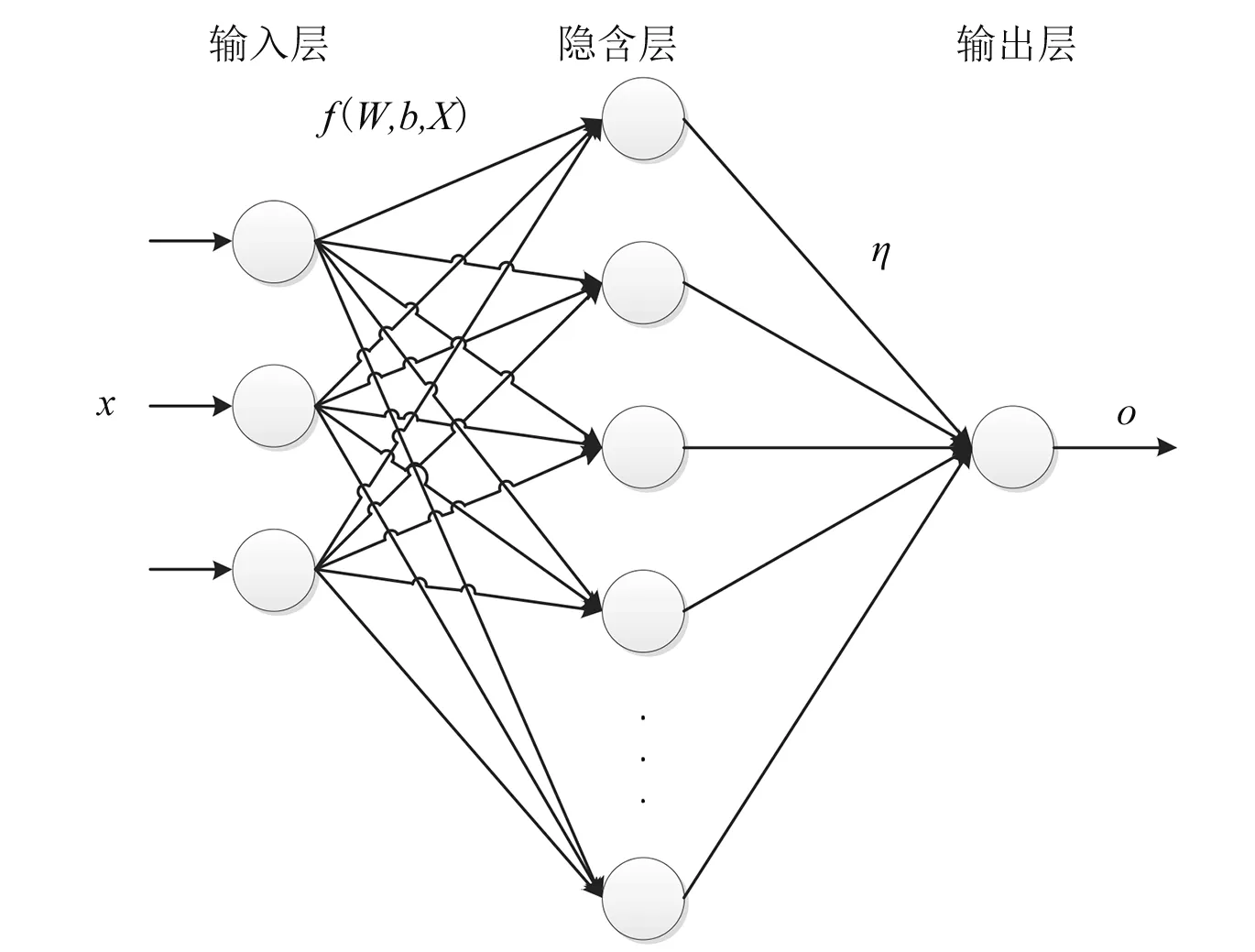
图1 经典ELM结构图
(4)
式中:Wj为第j个隐含层神经元与输入向量Xi间的权值向量;bj为第j个隐含层神经元的阈值;ηj为第j个隐含层神经元与输出层节点间的权值;oi为第i个样本的输出。
3 正则化优化ELM算法的光伏功率预测
3.1 预测流程
如图2所示,首先需要整理辐照量等特征向量的时间序列,对整理出来的数据进行归一化处理,处理后的数据划分为训练集和测试集。训练集决定最优的隐含层节点数、确定正则化参数并进行正则化过程。然后,解出对应的η。最后,把得到的参数使用到测试集中进行预测。

图2 正则化优化ELM算法预测流程图
具体为:①由于天气因素与设备因素均对预测结果产生影响,选定历史发电数据量、总辐射量、直射辐射、散射辐射、环境温度、风向(力)、气压、相对湿度、组件的温度和组件的电流电压等参数为特征向量。整理辐照量等特征向量的时间序列,对整理出来的数据进行归一化处理,把处理过的数据分成训练集和测试集。②先通过训练集决定最优的隐含层节点数,然后确定最优正则化参数,再进行正则化过程,最后将得到的参数使用到测试集,进行预测。③通过相关误差系数评价预测结果的精度。
3.2 误差评价
本文在评价仿真预测结果精度时使用均方误差MSE与决定系数R2。
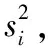
(5)
决定系数,也称为判定系数或者是拟合优度。当R2趋近于1时,说明相关方程越值得参考;相反,趋近于0时,说明相关的方程没有参考的意义。
在多元回归分析中,决定系数是通径系数的平方,其表达式为:
(6)
式中:SST为总平方和;SSR为回归平方和;SSE为残差平方和。SST=SSR+SSE,拟合优度越大,自变量对因变量的解释程度越高,观察点在回归直线附近越密集。
决定系数:为0时,表示模型效果跟瞎猜差不多;为1时,表示模型拟合度较好;在0~1时,表示模型的好坏(针对同一批数据);小于0时,说明数据不存在线性关系。
4 仿真分析与结果
本文数据使用的是澳大利亚DKA太阳能中心提供的某地区光伏发电站2018年1月1日至2018年12月31日的历史数据。选取的时间间隔为5 min,选取的数据共105 230组。由于光伏发电受自然因素影响较大,尤其是辐射量、温度、风向、风力和相对湿度。因此,综合考虑,每组数据选定的特征向量包括:历史发电数据量、总辐射量、直射辐射、散射辐射、环境温度、风向(力)、气压、相对湿度、组件的温度和组件的电流电压等参数。训练集数据为105 000组,测试集数据为230组。利用MATLAB仿真软件进行了光伏发电功率值的仿真预测和相应的评价值计算。
4.1 仿真结果分析
图3为正则化优化ELM预测波形与真实波形图,图4为ELM预测波形与真实波形图。图3、图4中横坐标为测试集样本编号,纵坐标为光伏发电功率。通过计算得到,正则化优化ELM预测波形预测结果均方误差为0.002 58,决定系数为0.999 97。ELM预测波形预测结果均方误差为0.011 18,决定系数为0.999 89。
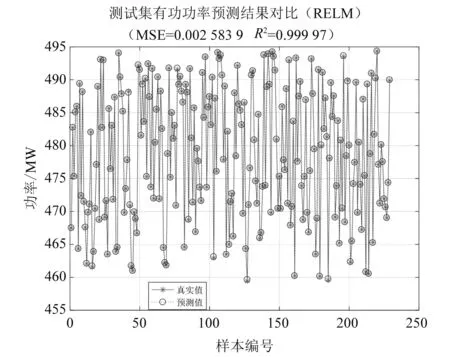
图3 正则化优化ELM预测波形与真实波形
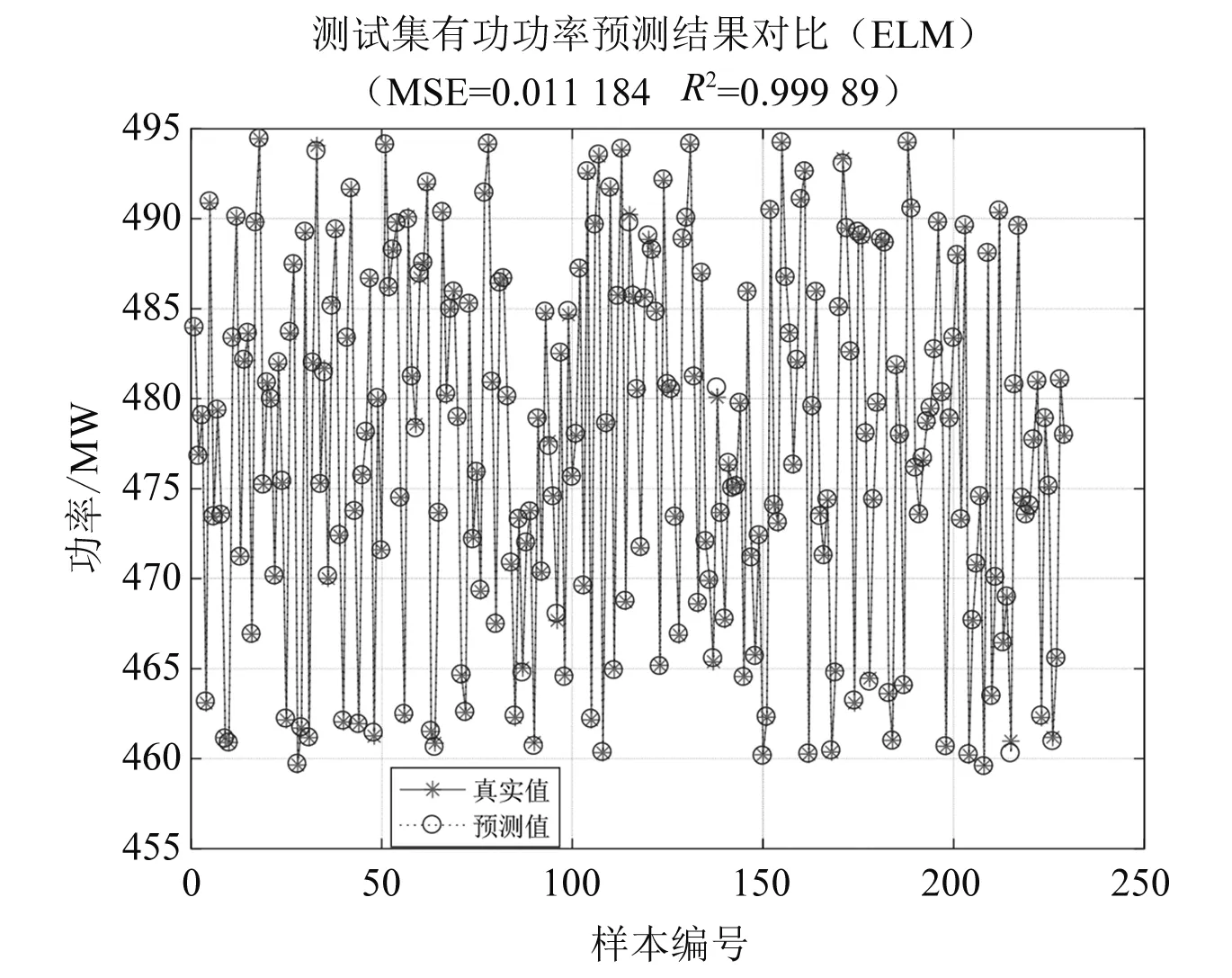
图4 ELM预测波形与真实波形
4.2 仿真对比
对比两种方法预测结果的评价值可知,优化前的预测结果中,均方误差为0.011 18,决定系数为0.999 89,优化后的预测结果中,均方误差为0.002 58,决定系数为0.999 97。均方误差降低了0.008 6,决定系数提高了0.000 05。由仿真波形图可知,预测的精度得到改善。
5 结束语
极限学习机(ELM)是一种前馈神经网络,克服了传统神经网络学习算法(如BP算法)极易陷入局部最优、学习速度慢的缺点。利用正则项化处理数据的特点,对ELM进行优化,最终解不会过拟合,可以提高预测的精度。本文使用实际的历史发电数据以及历史天气数据,以正则化优化ELM算法进行光伏发电功率预测。利用MATLAB仿真软件进行了光伏发电功率值的仿真预测和相应的评价值计算。最后,通过仿真波形图验证,该方法可以改善预测的精度。

