一类带有Robin边界条件的分数阶对流弥散方程的差分方法

尹修草，刘桃花

(湖南科技大学 数学与计算科学学院，湖南 湘潭，411201)

近十多年来，分数阶微分方程在物理、数学、化学、医学、环境科学以及金融等学科中得到了广泛的应用[1-5]，因此，分数阶方程及其应用得到了广泛的关注。分数阶微分方程是整数解微分方程的扩展，它能获取时间和空间上的非局部关系，为描述不同物质的记忆和继承性质提供了强有力的工具。由于分数阶偏微分方程的解析解大多难以得到，或者解析解太复杂导致难以计算，因此，研究者越来越关注分数阶微分方程的数值解法，其中，用有限差分方法求解分数阶微分方程是经典方法之一[6-11]。

本文考虑了一类带有Robin边界条件的分数阶对流弥散方程。XIE等[12]在研究广州市空气污染时，在经典的分数阶对流弥散方程中加了一项耗散项得到了该方程，并讨论了此方程带Dirichelet边界条件的有限差分方法以及此方程在广州市空气污染时的应用。刘桃花和尹修草[13]在研究长株潭PM2.5污染时，考虑了此方程带分数阶边界条件的应用。曾宝思等[14]指出带Robin边界条件可以用来描述介质的反常渗透现象，并给出了带Robin边界条件的经典分数阶对流弥散方程的数值解法。本文考虑带Robin边界条件此类对流弥散方程有限差分方法，建立了有效的数值格式，分析了该格式解的存在性、稳定性以及收敛性，并通过数值试验来验证格式的有效性。

考虑带Robin阶边界条件初边值问题的分数阶对流弥散方程：

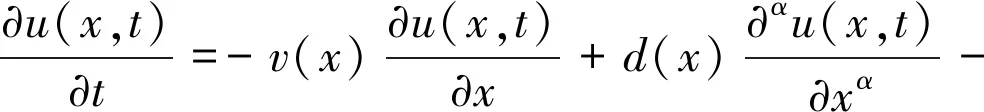
(1)

Robin初边值条件为

(2)

u(x,0)=q(x)，0≤x≤R

(3)

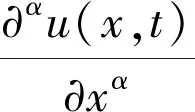
(4)

其中：Γ(·)为Gamma函数。XIE等[12]讨论了式(1)带Dirichelet边界条件的有限差分方法，本文考虑式(1)带Robin边界条件的有限差分方法，且只讨论β>0时的情况。

1 移位的Grünwald-Letnikov分数阶算子近似的差分方法

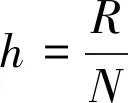
引进移位的Grünwald-Letnikov分数阶算子[15]：

(5)

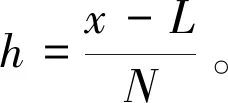
(6)

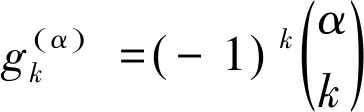
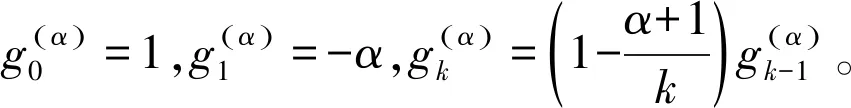
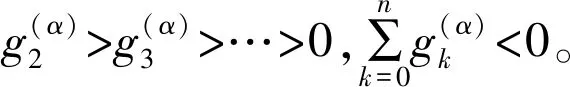
用移位的Grünwald-Letnikov分数阶算子对式(1)中Riemann-Liouville分数阶导数进行离散，一阶向后差分算子对Robin边界条件式(2)中导数进行离散，对式(1)～(3)建立隐性Euler差分格式如下：

(7)

(8)

(9)

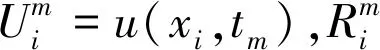
当1≤i≤N-1时，局部截断误差为

(10)

当i=N时，局部截断误差为

(11)

由此可知，所建立隐式差分格式与方程是相容的。

2 含移位的Grünwald-Letnikov分数阶算子近似的差分方法稳定性和收敛性分析

(12)

(13)

进一步将分数阶方程改写成下列矩阵的形式：

AUm=Um-1+Fm,1≤m≤M

(14)

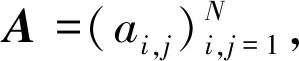
(15)

定理1 含移位的Grünwald-Letnikov分数阶算子近似的差分格式差分格式(7)～(9)的解存在且唯一。

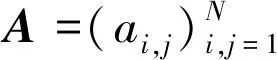
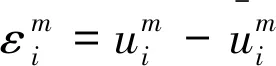
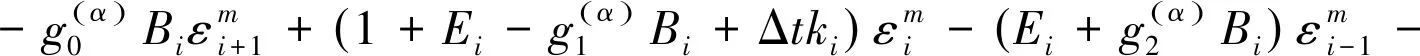
(16)

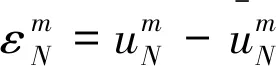
(17)

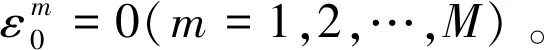
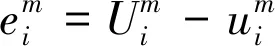
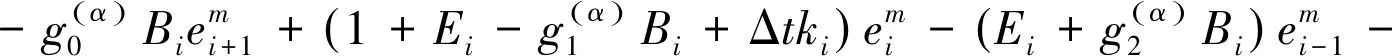
(18)

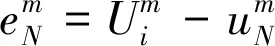
(19)

定理2 含移位的Grünwald-Letnikov分数阶算子近似的差分格式(7)～(9)是无条件稳定的。

证明由式(17)可得

(20)

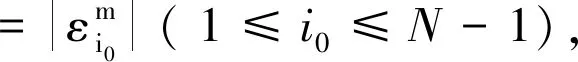
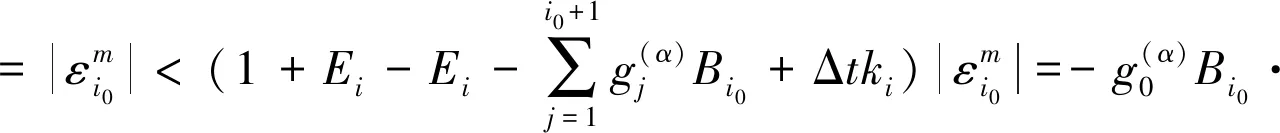
(21)

运用式(21)m-1次，可得

‖εm‖∞<‖ε0‖∞,1≤m≤M

综上所得，含移位的Grünwald-Letnikov分数阶算子近似的差分格式(7)～(9)是无条件稳定的。

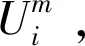
‖em‖∞≤C(Δt+h),1≤m≤M

(22)

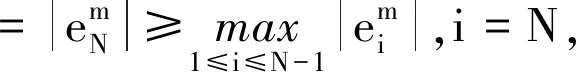
由式(19)可知

因此，存在一个正的常数C1,有

(23)

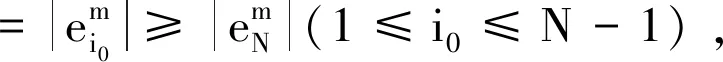
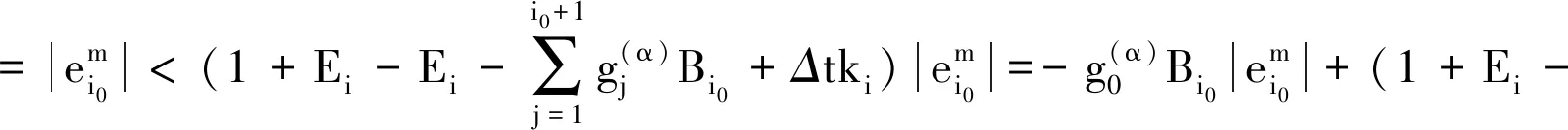
(24)

运用式(24)共m-1次，则有

‖em‖∞≤(m-1)ΔtC2(Δt+h)

又因为(m-1)Δt≤T，T为t的右边界，见式(1)，所以，存在1个常数C3=C2T，使得

‖em‖∞≤C3(Δt+h)

因此，此格式是收敛的，

取C=max{C1,C3}，且存在这样的一个正常数C，使得

‖em‖∞≤C(Δt+h)

3 数值试验

考虑如下的分数阶对流-弥散方程:

(25)

Robin初边值条件为

u(x,0)=5x(1-x)，0≤x≤1

式(25)的精确解为:u(x,t)=5e-t(x-x2)。

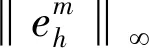
表1 当T=1时隐式差分格式的误差值Table 1 Error behaviors for the implicit finite difference solution under T=1

从表1可以看出，含移位的Grünwald-Letnikov分数阶算子近似差分方法的收敛阶为O(Δt+h)。

4 结论

本文考虑带Robin边界条件此类对流弥散方程有限差分方法，建立了含移位的Grünwald-Letnikov分数阶算子近似的隐性Euler差分格式，分析了该格式解的存在性、稳定性以及收敛性，并通过数值例子来验证了Euler差分格式的有效性。