一类线性回归模型的参数估计

甘胜进，王琼瑾

(1.福建师范大学福清分校电子与信息工程学院，福建 福清 350300；2.台湾政治大学统计学系，台北 11605；3.华东师范大学经济与管理学部统计学院，上海 20062)

经典的多元线性回归模型y=β0+βTX+ε，其中响应变量y是一维，p维解释变量X=(x1，x2，…，xp)T，误差ε的数学期望为0、方差为σ2.为了较方便获取回归系数的样本估计量性质，通常假设X是确定性变量[1-2]，或者假定是随机变量，但未给出其估计量渐近分布[3].本文考虑一类特殊多总体线性回归模型，并且假定解释变量X是随机的，每个子总体上有部分变量的回归系数相同，具体地来讲，在第i个子总体下:

(1)

1 估计量及其渐近性质

在导出估计量渐近分布之前，有必要对一些符号作如下说明.

cov(X2)=Σ22， cov(X1，X2)=Σ12，

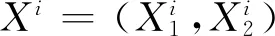
(2)

这里，投影矩阵

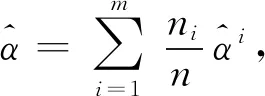
引理1当ni→∞ 时，

依分布收敛．

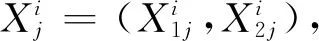
根据引理1，当ni→∞ 时，可得下式：

(3)

(4)

(5)

直观上讲，依据 (3) 式，

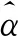
其中，

故

其中，

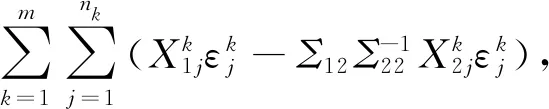
基于以上讨论，根据中心极限定理可得以下定理．

其中，

由定理1可知，

其中，

不难看出，新估计量与原估计量渐近方差差别为一个半正定矩阵，结合 (4) 式和定理1可知，当X1与X2不相关时，新估计量只对α有改进效果，对βi不起作用.事实上，无论X1与X2关系如何，增加样本容量导致方差减小，如果X1与X2不相关，那么X1不能提供有关X2的任何线性信息．

2 随机模拟

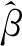
模型1X=(X1，X2，…，X5)T～N(0，Σ)，其中,

ε～N(0，1)，X与ε相互独立.

组1:Y=6X1+8X2+19X3+X4+4X5+ε；

组2:Y=6X1+8X2+26X3+23X4+12X5+ε；

组3:Y=6X1+8X2+25X3+16X4+10X5+ε；

组4:Y=6X1+8X2+15X3+14X4+30X5+ε；

组5:Y=6X1+8X2+2X3+18X4+7X5+ε；

组6:Y=6X1+8X2+5X3+22X4+9X5+ε．

图1表示模型1中100次蒙特卡罗模拟下两种估计方法各组参数的均方误差的箱线图，每次模拟样本容量组1至组6分别为50、55、60、65、70、80.右上标为old表示在各个组内利用最小二乘估计方法，右上标为new表示本文建议的方法，其中每组前四个箱线图分别是共同参数6、8两种方法估计比较，后6个则依次是不同三个系数估计性能比较，通过箱线图可知，本文建议的方法明显好于直接利用组内最小二乘估计方法，而且相同系数估计远优于不同回归系数估计，这是因为相同部分利用了更多样本，估计量方差更小．

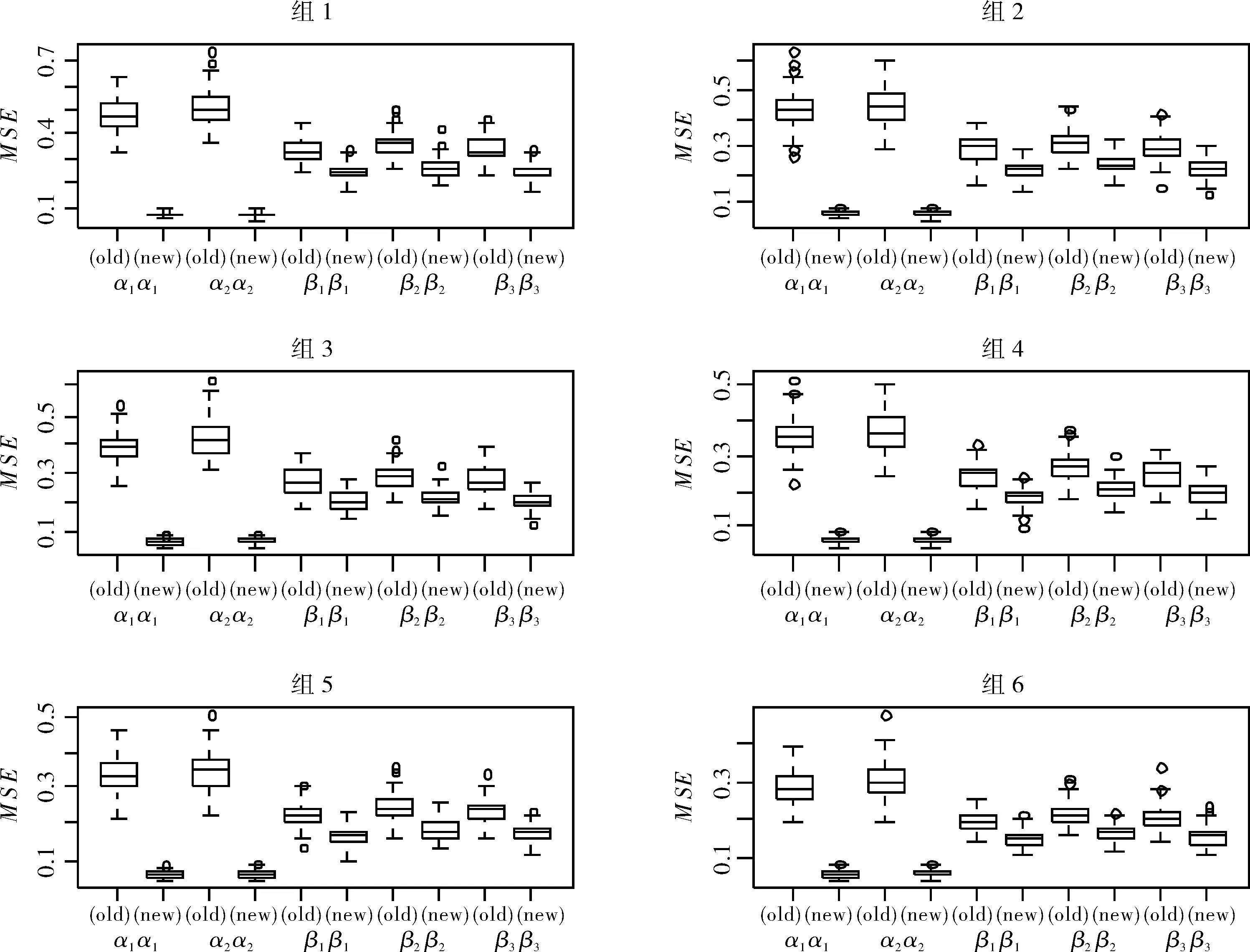
图1 模型1中各组新方法与原方法估计参数的MSE箱线图Fig.1 Boxplots of MSE between new method and old method in parametric estimate under model 1

模型2X=(X1，X2，…，X5)T～N(0，Σ)，其中,

ε～N(0，1)，X与ε相互独立.

组1:Y=-X1+X2+1.98X3+0.42X4+1.76X5+ε；

组2:Y=-X1+X2-1.9X3+X4-1.7X5+ε；

组3:Y=-X1+X2-1.6X3+0.18X4+0.85X5+ε；

组4:Y=-X1+X2-0.93X3+1.28X4+0.92X5+ε；

组5:Y=-X1+X2+0.65X3-1.2X4+1.85X5+ε；

组6:Y=-X1+X2-1.17X3+1.69X4-1.87X5+ε．

图2为模型2下100次蒙特卡罗重复两种方法估计的箱线图，每次模拟组1至组6样本容量分别为100、150、200、250、300、350.从图中可知，当公共回归系数对应回归变量与不同系数对应的回归变量之间无相关性时，本文建议的方法仅对公共回归系数估计有效，不同部分估计效果变化不大，印证了定理1．

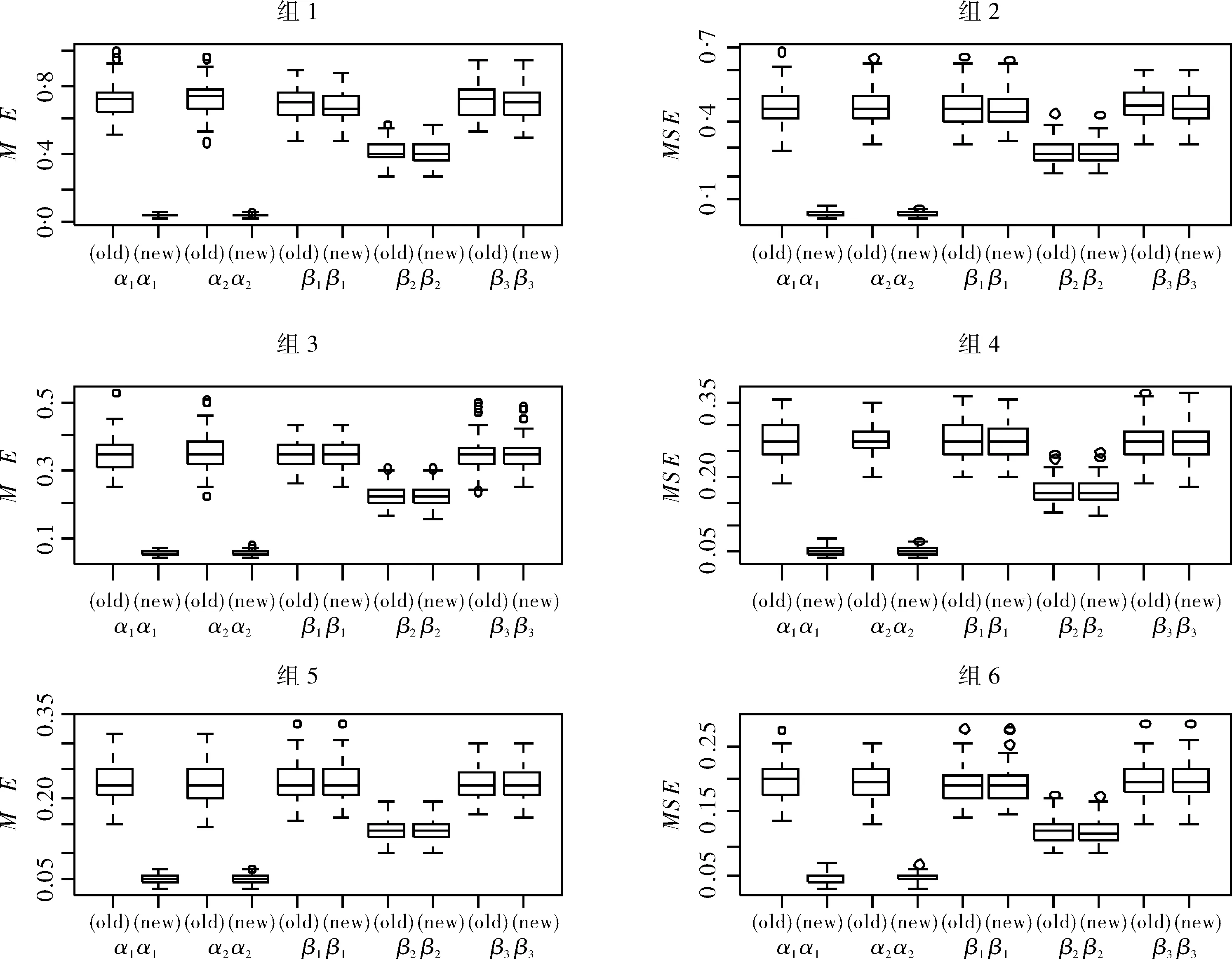
图2 模型2中各组新方法与原方法估计参数的MSE箱线图Fig.2 Boxplots of MSE between new method and old method in parametric estimate under model 2

3 结语

本文给出了多总体部分公共系数线性回归模型估计方法，并给出该方法估计量的大样本性质，其渐近方差小于直接利用最小二乘估计，蒙特卡罗模拟进一步证实了该结论.本文方法在大数据时代意义比较明显，假设每个子总体代表每个相距较远地区，每个地区产生符合该模型的数据量非常大，现在要估计各个子总体模型中参数，本文建议的方法只需要在各个子总体内估计参数，处理后的参数传输到后台，后台通过加权平均估计出公共参数，然后传输到各个子总体估计不同部分参数，整个过程只须传输参数，避免了大数据传输带来的各种问题.其流程图如图3．

图3 算法示意图Fig.3 Diagram of algorithm

算法的另外一个优点是各个子总体内运算是并行的，可以极大地减少计算时间．