具有非线性发生率和Markov切换的随机SIRS传染病模型*
何雪晴,韦煜明
(广西师范大学 数学与统计学院,广西 桂林 541000)
1 引言及预备知识
文献[1]和[2]研究出的传染病仓室模型和阈值理论,是传染病动力学发展的良好开端。于是,许多研究者们纷纷建立了大量的流行病模型,如SIS、SIRS、SIER和SIQR等。[3-6]因为发病率函数对环境波动具有一定的影响,所以为了合理描述疾病的流行动态,文献[5]中就提出了最为典型的具有饱和发生率的SIRS传染病模型

然而它没有考虑外界环境的随机效应,因此如果设疾病的接触率β能在不同环境状态下随机切换,那么模型(1)就可以建立具有Markov切换的SIRS传染病模型,类似于文献[6]。此外,发现由感染者或易感者的相互作用,疾病发生率的非线性形式更符合实际,而在许多传染病模型中,部分病毒存活的时间短,所以在短时间内将疾病的接触率β随机扰动将更具有现实意义。因此,本文将研究具有感染者和易感者相互作用的非线性发生率的传染病模型,它的接触率β不仅可以在不同环境状态之间随机切换,而且还可以在短时间内进行随机扰动。
下面假设在连续时间Markov链r(t),t>0的任意相邻两次跳跃之间,接触率β也会受到短时间内的Gauss白噪声扰动,如果将系统外部环境条件分为E种不同状态,记为Μ={1,2,…,E},并且假设不同环境状态之间的切换与系统的状态相互独立,每个环境状态的停留时间服从指数分布,则在每一个环境状态e∈Μ下,令β=βe+σeξ(t),ξ(t)表示均值为0、方差为1的Gauss白噪声,正常数σe是白噪声在环境状态e下的波动强度,根据文献[7]可知ξ(t)dt=dB(t),B(t)是一维标准的Brown运动。由此,我们建立了一个具有非线性发生率和Markov切换的随机SIRS传染病模型
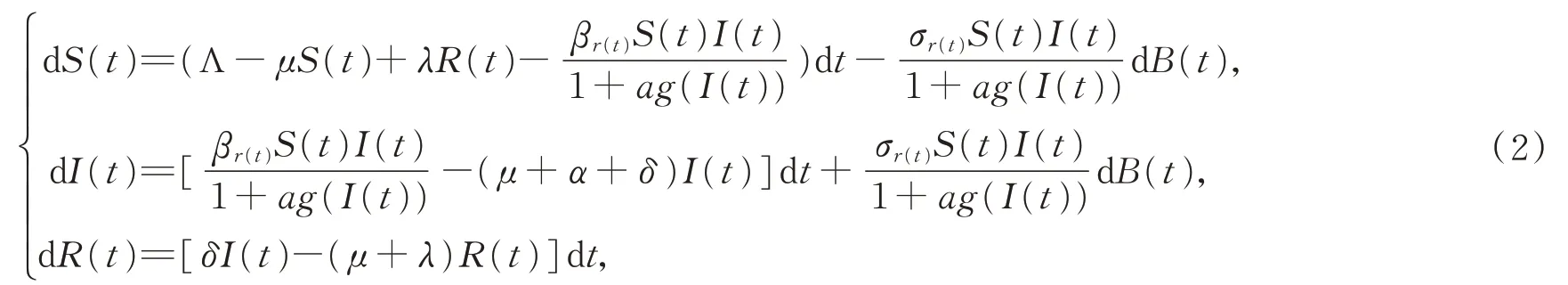
其中,S(t),I(t),R(t)分别代表t时刻的易感者人数、染病者人数和康复者人数。Λ是单位时间内的人口输入常数;μ是自然死亡率;λ是恢复者的免疫丧失率;α是因病死亡率;δ是染病者的恢复率。对于函数g(I(t)),我们做如下假设

(2)g(I(t))在R+上满足Lipschitz条件,并且对任意的I(t)>0,都有0<g(I(t))≤g"(0)I(t)。

2 全局正解的存在唯一性及有界性
定理1对任意给定的初始值(Z0,r(0))∈R+3×Μ,模型(2)在t≥0时,存在唯一的全局解Z(t)=(S(t),I(t),R(t))∈R+3,a.s.。
证明:由模型(2)的系数满足局部Lipschitz条件知,对任意给定的初始值(Z0,r(0))∈R+3×Μ,当t∈[0,τe)时,模型(2)存在唯一的局部解(Z(t),r(t)),其中τe表示爆炸时间。要证随机模型(2)存在唯一的全局解,只需证τe=∞,a.s.。


3 疾病的灭绝性
在讨论疾病的灭绝性之前,我们先给出一个引理,以便于对疾病灭绝所需要的充分条件进行证明。
引理3设Z(t)=(S(t),I(t),R(t),r(t))是模型(2)的解,初值为(S(0),I(0),R(0),r(0))∈Γ,其中Γ={(S(t),I(t),R(t),r(t))∈R+3×Μ:S(t)+I(t)+R(t)≤1}是一个正不变集,则

对(7)式两端从0到t积分并同时除以t,有

4 疾病的持久性

5 数值模拟
根据以上讨论,下面将利用文献[11]中的方法对模型(2)进行数值模拟。
设连续时间Markov链{r(t),t≥0}只有两个环境状态Μ={1,2},如果固定环境状态e∈Μ,则模型(2)的

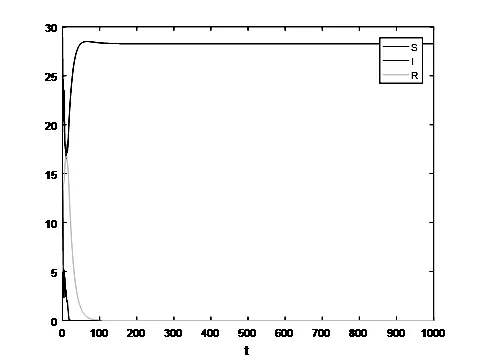
图1 疾病在状态1的情况下几乎必然灭绝

图2 疾病在状态2的情况下保持平均持久性
若取π=(π1,π2)=(0.5,0.5),则R*≈1.3>1,S(t),I(t),R(t)在状态1和状态2之间随时间t的变化如图3所示,疾病随机持久;若取π=(π1,π2)=(0.2,0.8),则R*≈0.9<1,S(t),I(t),R(t)在状态1和状态2之间随时间t的变化如图4所示,疾病随机灭绝。
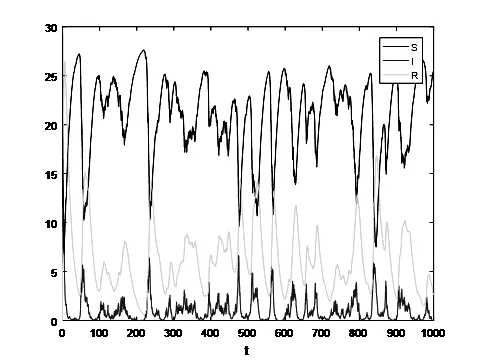
图3 疾病在状态1和状态2之间随机持久

图4 疾病在状态2和状态2之间随机灭绝

