混凝土重力坝深层抗滑稳定模糊体系可靠度研究

张建胜

(赣州市水利电力勘测设计研究院，江西 赣州 341000)

随着社会的不断发展，人们将一些资源的开发与利用向可循环方向发展，例如水资源的利用与开发需要建设一定规模的水电工程，同时还需要防止重力坝产生水患。常见的混凝土重力坝具有结构简单、适应能力强、便于问题解决与管理等优点，但是由于重力坝深层长期受水压力、泥沙摩擦的冲击与负载，重力坝可能会出现基面滑动与失稳现象。近些年来人们对混凝土重力坝深层抗滑稳定的研究越来越成熟，国内外采取大量的先进技术对混凝土重力坝深层抗滑稳定性进行改善。

较为常见的混凝土重力坝深层抗滑稳定设计方法有文献[1]中的刚体极限平衡法，这种方法长期应用在各项工程建设中，具有较成熟的理论、技术标准与建造经验，在此方法中需要将混凝土重力坝视为刚体，不考虑混凝土重力坝在长期水压作用下的形变，刚体极限平衡法能分析出重力坝在不同区段的水流中最佳倾斜角度，能够较准确地实现稳定可靠的混凝土重力坝建设。文献[2]中的改进有限单元法，考虑到混凝土重力坝结构材料的不同，可以模拟出重力坝深层的应力，还能够进一步探索重力坝本体的破坏机理，减少工程建设中存在的偏差。

本文则基于模糊体系对混凝土重力坝深层抗滑稳定可靠度进行研究，验证本文研究方法的有效性与稳定性。

1 混凝土重力坝深层抗滑稳定可靠度理论研究

在设计混凝土重力坝深层抗滑稳定结构时，需要考虑到多种阈值因素的影响，通过对结构中阈值因素的分析，使混凝土重力坝在建设后实现长久稳定工作，因此可靠度理论的形成需要由不同结构的混凝土重力坝极限工作状态组成随机变量，从而以可靠度理论的函数方式表现，设定混凝土重力坝深层抗滑稳定建筑的两侧结构基本变量为X1、X2、X3、…Xn，混凝土重力坝的工作状态函数用Z表示，则混凝土重力坝两侧的可靠度函数可以表示为

(1)

混凝土重力坝结构的工作临界值为Z=0。

在实际的混凝土重力坝建设过程中常常有多种不明因素对工程实施造成影响，这些不确定因素会导致结构设计的参数与设计标准具有模糊性，通过对混凝土重力坝可靠稳定度的极限值分析可知混凝土的建设结构稳定需要依靠较为精准的极限状态值。传统的模糊性分析只需依靠可靠稳定值的临界状态完成划分，但在混凝土重力坝深层抗滑稳定结构的具体建设中通过获取可靠状态与破坏状态的计算值，能够解决模糊范围问题[3-4]。图1为结构状态比较。

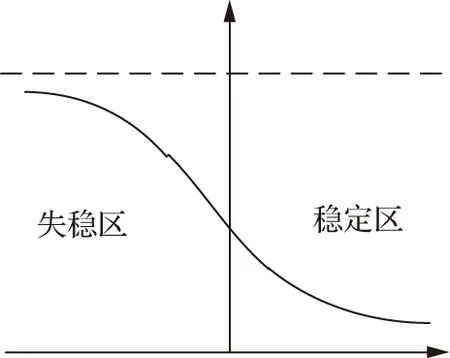
图1 结构状态比较

结构的模糊随机临界状态可以表示为

Z=g(x1,x2,…,xn)=b

(2)

式中g——模糊函数中的随机性功能；

x——模糊范围中的随机变量；

b——临界状态值[5]。

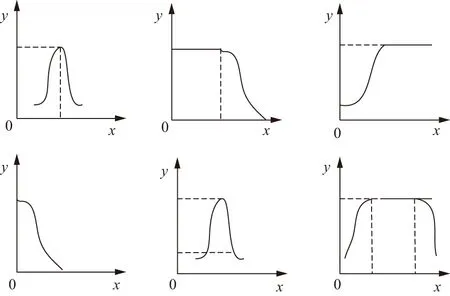
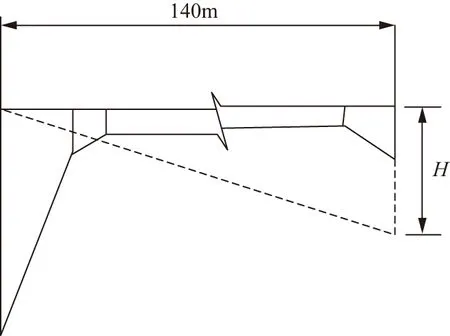
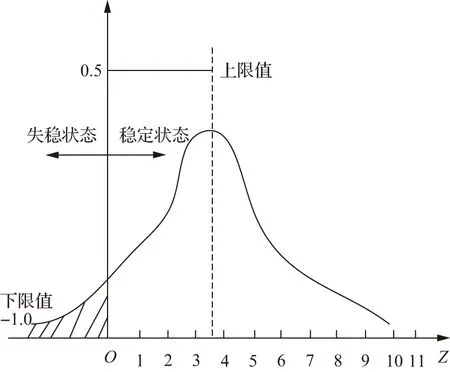
当临界状态值与函数Z不相等时会出现两种可靠性问题，Z>b代表混凝土重力坝结构处于稳定可靠状态，Z

图2 函数的模糊参数具体表现

模糊体系本身是一种模糊概念，对于复杂结构的运算还不能够实现精准化，在混凝土重力坝深层抗滑稳定模糊体系中增加一项重力坝的水平截面算法与实效准则隶属函数的参数将会显著提升符合工程的模糊可靠值[6-7]。

2 混凝土重力坝深层抗滑稳定模糊体系可靠度分析

2.1 混凝土重力坝深层基面模糊可靠度分析

混凝土重力坝深层抗滑稳定模糊性较为复杂，在体系的分析中存在着大量的模糊因素以及技术参数，本文将数学领域的模糊性算法融入混凝土重力坝基面的建设中，并引用失效准则与随机变量体现模糊性在混凝土重力坝深层基面的结构分析效果。我国采用的混凝土重力坝大多数为两侧结构不同的基面结构，但是在实际的结构建设中具体的技术标准范围通常是模糊的，所以可以将混凝土重力坝深层抗滑稳定性视为模糊事件，应用重力坝在工作中具有的失稳概率分析隶属函数中存在的参数与水压的摩擦系数[8-9]。

失效准则法与随机变量法在模糊条件下可以转化为水平截面积算法，利用混凝土重力坝基本计算条件计算模糊状态下的深层基面稳定程度，这种模糊条件运算方法是一种运算方式简单、实用程度高的方法，且能够通过人为经验改变算法中存在的风险，虽然在模糊状态下误差是必然存在的，但是降低算法的风险率能够更精准提升基面建设的参数设计与技术标准设计。本文选择正常状态下的混凝土重力坝深层基面结构进行研究，选取模糊功能函数如下：

Z=R-S-b

(3)

式中R——基面的水压面积；

S——模糊函数在深层中存在的模糊范围；

b——标准技术参数。

函数计算会减少非敏感因素的影响，当模糊变量开始建立独立功能函数时采用截面计算完成失效概率的结果认定。表1为不同水平截面的参数模糊范围。

表1 不同水平截面的参数模糊范围

再使用Matlab软件对模糊范围数据可靠度进行处理(见图3)。

图3 相关数据的重力坝可靠度模糊程度对比结果

根据图3的对比结果可知采用水平截面方法计算失效准则与随机变量模糊程度后所对应的模糊区间能够及时反映混凝土重力坝的失稳情况，与传统的计算方法相比此方法更加符合施工现状。图3中水平截面角度为0°时，混凝土重力坝可靠度两模糊临界值出现极差，在正常的混凝土重力坝深层基面结构中极少存在这种现象；当水平截面角度在45°以下时，模糊区间中的临界点向中间线贴近，此状态下的模糊数值符合重力坝深层基面结构的稳定可靠状态；当水平截面角度大于45°小于90°时，模糊区间的可靠度临界点向失稳状态贴近[10-11]。本文计算4种不同层次的混凝土重力坝水平截面积可靠度数据，比较全面地分析了模糊可靠度正常的模糊工作状态，由表1的计算数据可知水平截面算法下的模糊可靠稳定范围较小，进而能够确定此方法计算的基面分析结果失效概率较小，计算结果向安全稳定方向贴近。

2.2 混凝土重力坝深层整体结构可靠度模糊分析

在实际混凝土重力坝深层整体结构的建设工程中存在着大量的潜在不确定因素，这些不确定因素主要划分为参数随机性模糊和技术设计参数模糊，只有在可靠度模糊计算中给定设计整体结构技术参数与变量才能完整分析具有可靠度模糊计算的方差与均值，在达到可靠度极值计算结果前计算可靠值的标准指标。

本文首先应用模糊事件的普通计算方式作为样本数据的函数表现方式：

(4)

式中w——混凝土重力坝深层整体结构的特征参数；

P——函数中数学期望值。

若确定混凝土重力坝整体结构的模糊数据范围必须解决重力坝深层可靠度模型的基础数据问题，本文应用隶属函数来针对性地解决，隶属函数在模糊体系中的分析结果具有一定的主观性，常见的隶属函数确定方法有模糊统计方法、二元对比排序法以及待定系数法，这些方法在数据的评判方面是具有一定客观性的，一般的客观表现方式由六种曲线图组成，分别为正态曲线图、戒上型曲线图、戒下型曲线图、降半型曲线图、三角函数曲线图、区段型曲线图(见图4)。

图4 六种曲线

混凝土重力坝深层整体结构的可靠度模糊还可以以积分形式表达，整体结构具有失效状态与平衡状态两种，区别两种状态的方式主要为模糊极限状态的积分，分别对平衡状态与失效状态的整体结构可靠度进行积分化与函数化。正常状态下在模糊范围内使用结构的安全状态合集可以认定为确定安全事件的模糊公式，计算结构在水压中的抗性与随机性，应用计算数据描述模糊状态下的安全可靠状态。对于比较复杂的重力坝深层结构，模糊体系中的计算函数不能直接给出精准的参数范围，需要结合传统的理论技术与常规的参数合集对比并关联得到可以进行数据融合的模糊概率关系，将由水平截面积等方法获取的数据归纳至普通时间的模糊范围内，对结构可靠度数据信息处理完成拓展[12]。

2.3 混凝土重力坝深层结构稳定及应力模糊分析

江西省寻乌县黄坑水库地处寻乌县晨光镇黄坑村内，大坝距县城约 45km，大坝为混凝土重力坝，坝址以上集水面积14.1km2，坝顶高程为336.00m，最大坝高为29.5m，水库总库容为309万m3。根据地勘成果描述，左岸坝基约16m坝高段基础基岩倾角较缓(向下游倾角约10°)，倾向右岸，在NE、NW、近EW方向裂隙相互切割作用下对坝基稳定不利，建议进行复核。

混凝土重力坝深层结构的稳定复核需要通过各种运行工况下重力坝的抗滑稳定安全系数及应力来判断，根据《混凝土重力坝设计规范》(SL 319—2018)和《水工建筑物荷载设计规范》(SL 744—2016)，坝体抗滑稳定按抗剪断强度公式计算：

(5)

坝基法向应力按下式计算：

(6)

式中K′——混凝土重力坝在深层结构中受到剪应力表现的抗滑稳定安全系数；

f′、C′——深层结构的摩擦系数和黏结力；

A——抗剪应力面积；

∑W——法向分值；

∑P——切向分值。

混凝土重力坝在正常水位情况下的受力组成为荷载重力、静水压力、泥沙压力、浪冲击力等，计算参数：节理裂隙(岩块岩屑型)结构面抗剪摩擦系数为0.45，黏聚力为0.05MPa，混凝土重度为24kN/m3，基础岩块的重度为24.5kN/m3，水的重度取9.81kN/m3时，并从重力坝两侧计算不同角度下的缓冲力，当坝基角度向上游倾斜10°时，计算简图见图5。

图5 大坝深层抗滑稳定及应力计算断面 (单位：mm)

混凝土重力坝在各种工况下抗滑稳定可靠度数据见表2。

表2 可靠度数据计算结果

根据计算结果，该溢流坝抗滑稳定及地基面应力均能满足规范规定的要求。

3 实验研究

本文参考向家坝水电站中的金沙江混凝土重力坝深层抗滑稳定模糊体系研究成果，在相同的混凝土重力坝深层结构中实现不同技术方法下的可靠度性分析。由于金沙江上最高梯级重力坝高达160m，重力坝的地层构造复杂，重力坝深层构造主要由砂岩、泥岩等组成，深层构造水平截面角度波动较大，计算混凝土重力坝深层基面工况需要对300m高的上游水底下250m处的水压进行加载，通过查询资料，确定金沙江混凝土重力坝的底板浮重度为10kN/m3,江内泥沙摩擦角在15°～20°之间，利用这些地理位置不变的参数条件，完成数据类可靠性初步分析。图6为金沙江混凝土重力坝的水压分布图。

图6 金沙江混凝土重力坝的压力分布

对图中的压力分布进行可靠度的指标分析，应用迭代计算完成，计算步骤如下：

a.选取混凝土重力坝深层结构的水平面积a，计算水平面积在水平截面积函数中的结果。

b.假设混凝土重力坝深层结构的可靠度初始值为0，计算在这种情况下的水平截面积函数结果是否存在差异。

c.假设混凝土重力坝深层基面的可靠度初始值为0，计算这种情况下的水平截面积函数结果是否存在差异。

d.为了避免迭代数据运算过程中出现重复性的误差与可靠标准值，需要在选取约束参数值时确定迭代计算的步骤及进行结果的二次确定。

由于重力坝深层结构倾斜角的变化极大影响着可靠度，从安全角度分析需要从深层重力坝中选取常随作用力方向和滑动面改变的模糊数据，当角度选取为0°、30°、60°时的模糊可靠指标见表3～表5。

表3 0°模糊可靠指标

表4 30°模糊可靠指标

表5 60°模糊可靠指标

本文还对模糊体系分析算法进行了改进，在可靠稳定系数基础上实现新函数的运用如下：

(7)

式中的S、R分别代表混凝土重力坝深层结构的水平截面积与受力状态，应用这种极限状态的函数还需要对模糊参数范围实现区间确认，当函数结果大于模糊参数中的最大值时可以确定在混凝土重力坝深层结构中出现失稳状态，当函数结果在函数模糊体系范围内，便可以确定混凝土重力坝深层结构处于可靠度良好状态，其中具体的失稳状态参数还需要参照工程技术与实际地质状态。改进深层重力坝模糊可靠度范围以便能够完善模糊可靠度分析的数据完整性，实验中以水平截面积算法作为失效准则的基本隶属函数，作为重力坝可靠度的数据处理对象，同时应用文献[1]、文献[2]中的刚体极限平衡法以及有限单元法进行数据分析，为了能够凸显不同方法在分析效果的突出表现，将三种方法的模糊可靠度函数计算值表现在表6中。

表6 三种方法的可靠度分析结果

表6中的数据分析只针对混凝土重力坝深层失效准则隶属函数，取用三种方法相对的计算结果进行对比，能够体现本文方法在模糊程度方面的精准范围，若对模糊可靠度进行具体分析还需要精确到隶属函数中参数的上限值与下限值之间关系，其模糊可靠度分析结果见图7。

图7 模糊可靠度分析结果

从图7中的分析结果可知，本文采用的模糊体系分析方法在计算重力坝深层结构失稳极限值时比传统的方法极限值要高，随着隶属函数的迭代运算次数增加，函数迭代次数在3次至4次之间时可靠度值达到最佳状态，迭代次数达到9次以上时函数结果趋于稳定，模糊可靠稳定度的极限值越来越接近中间稳定值，且稳定值一直控制在0.5上限值与-1.0之间；这种模糊体系下的隶属函数还包括对混凝土重力坝在不同地质条件下的可靠度极限值，由于金沙江地区的河流类型丰富，运用模糊算法恰好能够补偿地质误差等外界干扰分析因素。

本文实验采用的主要为模糊体系中的水平截面积算法，并对算法中的函数进行了一定程度的改进，对模糊可靠度的复杂性与可逆性实现明确性协调。

4 结 语

本文主要对混凝土重力坝深层抗滑模糊体系可靠稳定度进行分析，将模糊体系引用到实际的重力坝深层结构参数分析中，在传统水平截面积算法基础上完成算法方面与极限值方面的改善。本文较全面应用模糊算法体系的可靠度分析理论，总结实际工程中存在的缺点，再结合重力坝在不同地区极限值的区别实现复杂地质条件下的可靠度分析。