基于高分五号DPC氧气A吸收波段的云顶压强反演

乔 瑞,伽丽丽,许 华,李正强∗,朱思峰,谢一凇,洪津,代海山,麻金继

(1中国科学院空天信息创新研究院,国家环境保护卫星遥感重点实验室,北京 100101;2中国科学院大学,北京 100049;3中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院通用光学定标与表征技术重点实验室,安徽 合肥 230031;4上海卫星工程研究所,上海 201109;5安徽师范大学地理与旅游学院,安徽 芜湖 241000)

0 引言

云大约覆盖了海洋面积的71.7%和陆地面积的58.4%[1],是影响全球辐射收支的关键因素,也是气候变化中最大的不确定性源[2]。云顶压强与云顶高度具有较稳定的对应关系,是重要的云物理参数之一。准确获取云顶压强对于天气预报尤其是强对流天气的监测预警有着重要的作用[3]。此外,利用云顶压强对一些较难识别的云(如薄云、高亮地表(包括冰雪)上空的云)有较好的识别效果。云顶压强还可作为一些高度特征明显的云(如卷云、深对流云等)分类的重要判据。

利用卫星数据反演云顶压强,主要有成像几何和通道辐射特性两类方法[4]。成像几何方法主要是利用不同卫星或同一卫星的不同角度对于同一目标的视差和卫星的位置来反演云顶高度,并转化为云顶压强[5]。而通道辐射特性方法主要有单通道或多通道亮温法[6]、分裂窗法[7,8]、CO2切片法[9,10]、偏振反射率法[11,12]和氧气A吸收带法等。

氧气A吸收带位于758～778 nm,此波长范围除氧气外几乎没有其他气体吸收,而氧气在大气中的含量比例稳定,所以该吸收带是一个反演云顶压强的理想通道[13]。利用氧气A吸收带反演云顶压强的想法最早由Yamamoto和Wark提出[14]。Kuze和Chance[15]利用SCIAMACHY的观测值和模拟计算的氧气吸收率通过最小二乘拟合获取了云顶高度。Br´eon等[16]利用POLDER传感器在氧气A吸收带的宽窄两个波段进行了表面压强反演的理论分析,其利用辐射传输模型进行正向模拟,得到两波段比值与压强的经验关系式,在POLDER云顶压强产品中得到了应用[17]。Preusker等[18]利用印度遥感3号卫星MOS传感器761 nm和765 nm波段的辐亮度比值计算了云顶高度。张岩等[19]对SCIAMACHY的两种经典云顶高度算法SACULA和FRESCO+的反演结果进行了比较,并用地基雷达和探空数据进行了验证。

高分五号(GF-5)卫星搭载的多角度偏振探测仪(Directional polarimetric camera,DPC),是中国第一个以气溶胶探测为目标的多角度偏振星载传感器[20]。GF-5位于太阳同步轨道,过境时间为当地时间13:30,重访周期为2天。DPC的波段设置和POLDER[21]相近,包括可见光至近红外的共8个探测波段(443,490,565,670,763,765,865,910 nm),其中490、670、865 nm波段为偏振测量波段,763 nm和765 nm波段位于氧气A吸收带上,带宽分别为10 nm和40 nm。DPC通过在卫星飞行过程中沿轨快速框幅式摄影,实现每个地面像元至少9个角度的观测。

本文在POLDER反演云顶压强[16]方法的基础上,利用DPC的763 nm和765 nm两个氧气A吸收波段,研究DPC云顶压强反演算法。主要考虑了DPC两氧气A吸收波段的仪器光谱响应函数,扩展了辐射传输模拟样本的海拔覆盖范围,改进了两氧气A波段反射率比值与表面压强经验关系的拟合公式,并对云顶压强反演进行了初步验证。文中,首先介绍了氧气A吸收带反演云顶压强的原理;然后,通过辐射传输模拟,得到DPC两个氧气A波段表观辐亮度比值反演云顶压强的拟合公式,校正了拟合误差,并简要分析了影响反演结果的其他误差因素,如大气气溶胶、大气廓线等;进一步,利用晴空地表对反演方法进行了稳定性分析和原理性验证(对比DEM),并比较了DPC云顶压强反演结果与MODIS云顶压强产品的一致性。最终,得到了分辨率和精度均较高的DPC云顶压强反演结果。

1 氧气A吸收带反演云顶压强的原理

氧气A吸收带波长范围为758～778 nm,是氧气吸收最强的一个吸收带,且在该吸收带内几乎没有其他大气吸收,比较“纯净”。GF-5搭载的DPC在氧气A吸收带设置了两个探测波段:一个是中心波长为763 nm的窄波段,覆盖了大部分较强的氧气吸收谱线;另一个是中心波长为765 nm的宽波段,覆盖氧气A吸收带的同时还覆盖了部分非吸收波段。因此,在传感器实际观测中,765 nm波段测得的表观辐亮度高于763 nm波段。图1为两个波段的光谱响应函数以及6S模拟的该波段整层大气氧气吸收透过率。

图1 DPC/GF-5 763 nm和765 nm波段传感器光谱响应函数及6S模拟的整层大气氧气吸收透过率Fig.1 Sensor spectral response and the total atmosphere oxygen transmittance simulated by 6S in DPC/GF-5 763nm and 765nm bands

某一波段氧气的吸收系数可以利用逐线积分法计算得到,假定波段内的每条谱线都是Lorentz型[22],则该波段的吸收系数k的计算公式为

式中:N为该波段范围包含的吸收谱线个数;Si为第i条吸收谱线的线强,是温度T的函数;ai为第i条吸收谱线的半宽,是气压P和温度T的函数;ν和ν0,i分别是该波段中心波数和第i条谱线的中心波数。

单一吸收谱线的线强Si和线宽ai的计算公式为

式中:S0为标准温度T0的线强,E为吸收光谱对应的电子跃迁低能级能量,a0为标准气压P0和标准温度T0下的半宽,这三个参数均为常数,对应的标准气压P0=1013 hPa、标准温度T0=273 K。

从上述公式可以看出,对于特定的波段,氧气的吸收透过率(可以由吸收系数计算得到)可以看作大气压强P和温度T的函数,而对于一个确定的大气温度廓线,氧气的透过率只和大气压强P有关。这样,可以利用氧气吸收影响权重不同的763 nm和765 nm波段观测值之间的对比关系,反演云顶(或晴空地表)大气压强P。

2 云顶压强反演方法

2.1 基于辐射传输模拟确定反演拟合公式

对于不透明的云,大气顶表观反射率可以认为大致由瑞利散射、气溶胶散射和云顶反射三部分构成,即

式中:tatm是云上大气透过率,在DPC的763 nm和765 nm波段内,该透过率主要受氧气吸收影响,其他大气分子的吸收如臭氧、水汽影响非常小(见表1)。

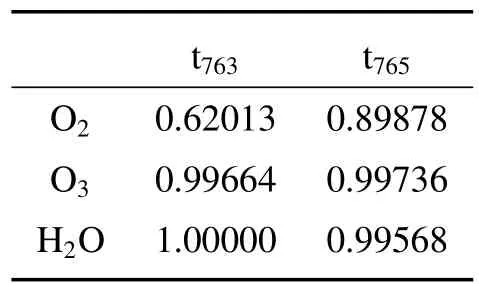
表1 6S模拟的DPC/GF-5 763 nm和765 nm波段吸收气体整层大气吸收透过率t763和t765Table 1 The total atmosphere transmittance t763and t765of absorption gases simulated by 6S in DPC/GF-5 763nm and 765nm bands

瑞利散射贡献Rrayleigh可以精确计算,其大小依赖于高度,在反演前是未知量,但由于这两个波段瑞利散射光学厚度很小(约0.02),该项对RTOA贡献也较小。气溶胶散射贡献Raerosol值依赖于云上气溶胶含量,在云层较高的情况下,该项对于RTOA的影响较小。云顶反射Rcloud难以精确计算,因为计算云层透过及内部多次散射的部分比较困难。对于本研究,由于两个波段非常接近,可以认为Rrayleigh、Raerosol和Rcloud在两个波段是相等的。

利用以上特性,定义比例系数X为763 nm与765 nm波段表观反射率的比值,其表达式为

根据上述分析,X≈tO2(763nm)/tO2(765nm),而不同高度大气中氧气比例恒定约为21%,氧气透过率tO2可以等价于云顶压强P,所以X与P存在函数关系。

辐射传输模拟时还需要考虑光程影响,定义大气光学质量m=1/µs+1/µν表示不同角度入射和反射光路的光程差异,µs为太阳天顶角的余弦,µν为观测天顶角的余弦。

为了得到X与P的函数关系,不考虑云层透过及内部多次散射的影响,利用辐射传输模型对比例系数X进行比较全面的模拟,压强P范围为1013.2～75.6 hPa(对应海拔高度0～18 km,步长1 km);大气光学质量m范围为2～5.84(对应太阳天顶角0～70°,观测天顶角0～70°,步长10°);云顶反射率设置为0.7;气溶胶光学厚度(Aerosol optical depth,AOD)值设置为0.1;大气模式设置为热带大气。

模拟结果如图2所示。由图2(a)可以看出mP与X有趋势上的关系,但比较离散,无法拟合出关系曲线。考虑到一定高度范围的氧气吸收光学厚度与气压存在近似的平方关系[23],故可以拟合mP2与X的关系曲线,如图2(b)所示。为了减少拟合偏差,尝试多种拟合模型后,选择用4次多项式进行拟合。拟合公式为

图2 763 nm和765 nm波段表观反射率比例系数X与大气光学质量m和大气压强P的关系。(a)X与mP关系;(b)X与mP2关系Fig.2 The function between X(ratio of 763 nm and 765 nm TOA)and m(air mass),P(atmospheric pressure).(a)Function of X and mP,(b)function of X and mP2

拟合相关系数R2=0.9995,说明X与mP2有非常强的相关性。拟合参数见表2。

表2 拟合公式(7)各项参数值Table 2 Fitting formula(7)parameters

2.2 拟合误差分析与校正

由于X与mP2的数量级相差较大,拟合误差的影响不可忽视,下面进行拟合误差分析和校正。

以太阳和观测天顶角均为0°、60°、70°为例,对于不同的X,用拟合公式得到mP2,计算压强误差相对值ΔP/P,得到误差趋势图(图3),其他天顶角的误差趋势与图3一致,其值介于0°和70°的样本曲线之间(类似图 3 中 60°样本)。

图3 不同太阳和观测天顶角(0°,60°,70°)压强拟合相对误差Fig.3 Relative error of pressure fitting at different solar zenith angles and view zenith angles(0°,60°,70°)

从图3可以看出,拟合误差主要和两个因素有关,一个是X的大小,另一个是太阳与观测天顶角。对于X,在X<0.9时,压强的拟合误差都较小,在±2%以内;而0.90.95时,误差均为正,且快速增大。对于角度,天顶角较小时拟合误差较大,而天顶角较大时拟合误差显著变小。这主要是因为角度的增大增加了光程,限制了X的增大。对反演来说,由拟合产生的误差主要会对云顶压强较小的情况(小于182 hPa,对应海拔高度约13 km以上)产生影响,而对于云顶压强较大的情形,则对反演结果影响较小。

因此,拟合误差的校正要同时考虑X和太阳、观测角度。对X>0.9的情况进行校正,角度通过大气光学质量m反映。为了减少多次计算引起的误差放大,直接对拟合项f(X)进行校正。定义误差校正量为Ecor,计算公式为

式中,m0和m70分别对应太阳和观测天顶角均为0°或70°时的大气光学质量(其值分别为2和5.8476),中间角度m的值介于m0和m70之间。拟合误差校正后P−X公式为

重新计算得到新的误差趋势图(图4)。可以看出,经过拟合误差校正以后,拟合误差在X>0.9时得到了显著降低,基本都小于1.5%,提高了反演的准确性。

2.3 其他因素误差分析

实际反演时,大气和地表情况各异,与拟合公式的模拟条件有差异,进一步分析由大气气溶胶、大气廓线和地表反射几方面因素带来的反演误差。

1)大气气溶胶

气溶胶主要分布在海拔3 km以下的大气中[24],对于具有一定高度且不透光的云来说,云上气溶胶影响一般很小。气溶胶对表观反射率的影响比较复杂,有散射、吸收、多次散射等效应。考虑到复杂性,利用辐射传输模拟计算其导致误差最大的一种情况,即考虑整层大气的影响。在实际反演中,误差都小于该情况。分析不同AOD时,利用式(11)反演云顶压强的误差,结果如图5所示。

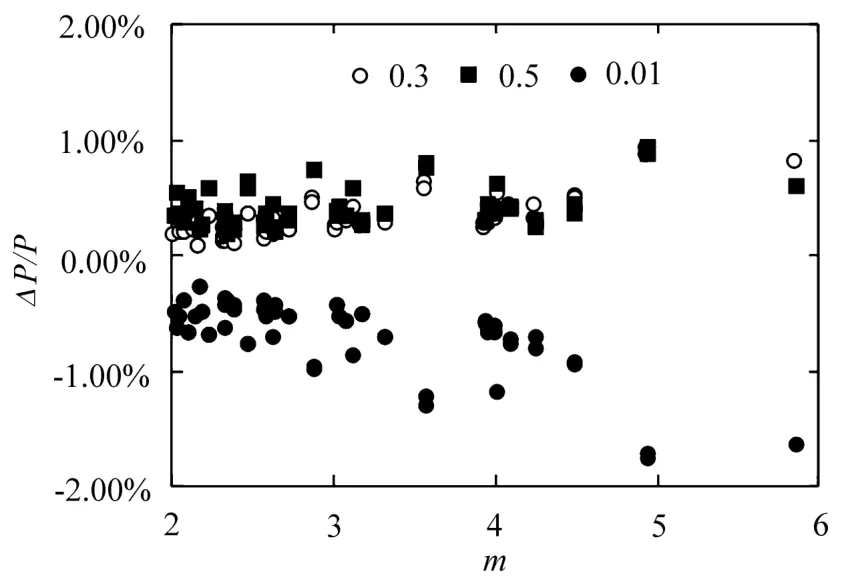
图5 不同AOD(0.01,0.3,0.5)时模拟反演的云顶压强相对误差Fig.5 Relative error of retrieved pressure for different AOD(0.01,0.3,0.5)

图5中,纵坐标为不同AOD值(0.01,0.3,0.5)时,基于拟合公式(11)(AOD值0.1)反演的云顶压强相对误差。可以看出,AOD大于0.1时,云顶压强反演结果偏大;AOD小于0.1时,云顶压强反演结果偏小;且相对误差均不超过±0.2%。因此,气溶胶含量对云顶压强反演结果的影响可以忽略。

2)大气温压廓线

利用拟合公式(11)模拟时选取的大气模式为热带大气,而地球上不同纬度和季节的大气廓线会有一些差异,例如极地附近的对流层高度比热带低的多,冬季的大气一般比夏季干燥等,尤其不同大气模式的温度压强廓线也有一定的差别。本研究采用的763 nm和765 nm波段,除氧气吸收外,其他气体(如臭氧和水汽)的吸收都很小,所以其他气体含量差异不会带来很大的误差。模拟五种不同的标准大气模式:热带大气(Tro)、中纬度夏季(MLS)、中纬度冬季(MLW)、亚北极区夏季(SAS)、亚北极区冬季(SAW)时763 nm和765 nm波段表观反射率,分析不同大气模式导致的云顶压强反演误差。

图6为其它四种大气模式时,基于拟合公式(11)(大气模式为Tro)反演的压强的相对误差。可以看出,大气模式差异会使压强的反演结果偏大或偏小,如大气模式为MLW时,在太阳和观测天顶角都为70°(m=5.8476)时压强的相对误差约为1.25%;大气模式为SAW时,在太阳和观测天顶角都为0°(m=2)时压强的相对误差约为−1.55%。总体来看,不同的大气模式所导致的压强反演误差约在±1.5%以内,影响较小。

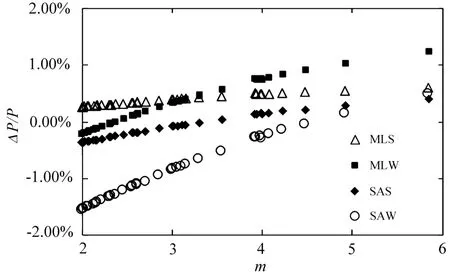
图6 不同大气模式(MLS,MLW,SAS,SAW)时模拟反演的云顶压强相对误差Fig.6 Relative error of retrieved pressure for different atmosphere profiles(MLS,MLW,SAS,SAW)

3)地表反射

对于光学厚度较小的云,一部分光会穿过云层经地表反射再被传感器接收。这样,反演得到的压强会介于云顶压强和地表压强之间,造成结果偏大。一方面地表类型复杂多样,另一方面薄云的性质也难以描述,很难定量研究地表反射对于反演误差的影响。因此,该算法对于不透光的厚云适用性更好。

3 结果与分析

3.1 利用晴空地表验证算法原理

本方法利用氧气A吸收带宽窄两个波段的比值来反演云顶压强(或表面压强),理论上可以用于任何下垫面(包括云顶或晴空地表)压强的反演[16]。因此,本小节采用晴空地表的观测对云顶压强(表面压强)反演算法进行原理性验证。

3.1.1 反演稳定性测试

由于云具有三维结构复杂且变化迅速的特点,为验证本反演算法在不同太阳、观测角度下的稳定性,选择DPC/GF-5同一晴空区域、不同观测日期的多角度观测数据,反演得到晴空地表的表面压强,并评估反演结果的差异大小。选择一个适合进行稳定性测试的区域:苏莱曼山脉东部(纬度范围30°N～31°N,经度范围69°E～70°E,海拔范围933～2352 m)。该区域为山地,地形复杂,能够较好地检验不同角度和日期情况下反演的稳定性。

图7为2018年5月27日和2018年11月29日两个不同日期对应的9个不同观测角度反演结果的差异系数(标准差与样本均值的比值,CV),横坐标表示不同样本。可以看出,大部分样本点不同观测角度反演结果的CV都小于4%。综合两个不同日期的平均CV为3.5%。个别样本点CV稍大,超过5%,最大达7.6%,但样本量较少,仅占总样本数的3.6%。这可能是山地复杂的地形结构导致DPC不同观测角度观测的地面目标有差异而造成的。

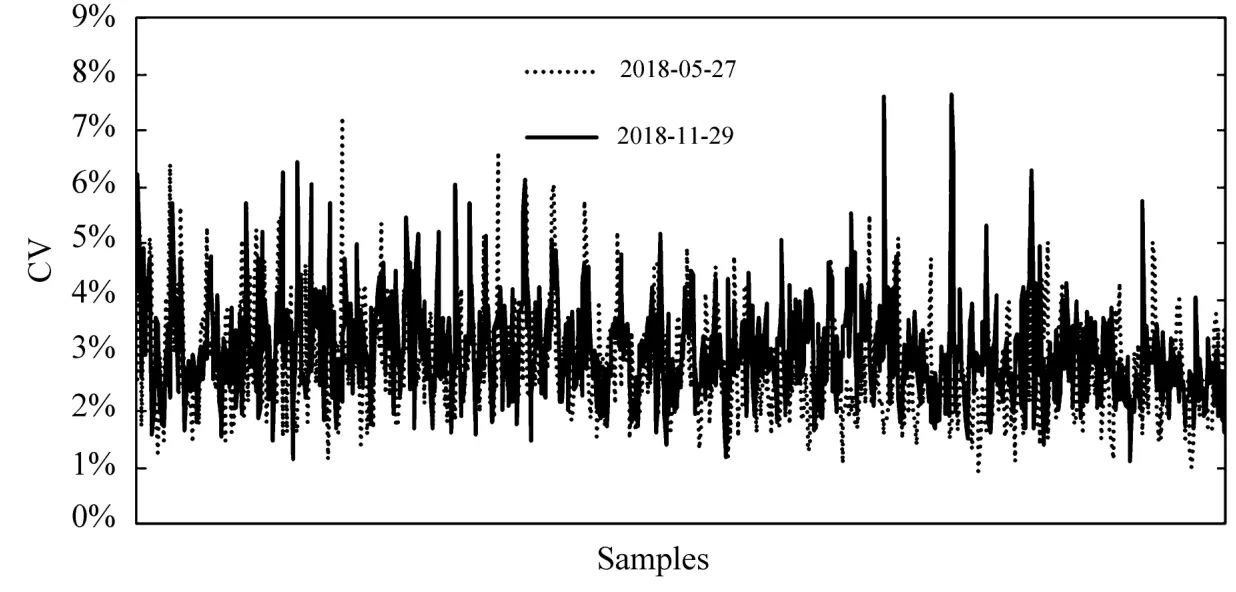
图7 DPC不同日期表面压强反演结果差异系数Fig.7 The coefficient of variation(CV)for DPC retrieved pressure from different dates

3.1.2 基于DEM的表面压强反演验证

忽略不同气压带和气象因素对于气压的影响,海拔高度与大气压强有着稳定的对应关系。因此,可以利用该反演方法得到陆地晴空区域的地表压强,与利用DEM估算的地表压强进行对比,验证算法反演结果的可靠性。其中,DEM数据可以从DPC 1级数据中获取,空间分辨率与DPC观测数据一致。利用DEM数据估算地表压强的公式为

选取一个海拔高度变化范围较大的地理区域(塔里木盆地和青藏高原交界处,纬度范围36°N～37°N,经度范围82°E～83°E,海拔范围1445～6286 m)为验证区域。数据观测日期为2018年5月27日。图8中横坐标为利用DEM通过高度-气压估算公式(公式12)估算的地表压强,纵坐标为DPC氧气A波段反演得到的地表压强。

图8 DPC反演的表面压强与DEM估算压强对比结果Fig.8 The comparison between DPC retrieved atmospheric pressure and DEM estimated atmospheric pressure

两个地表压强的线性拟合斜率k=1.115,截距b=−90.044,相关系数R=0.9421,说明DPC反演的地表压强与DEM估算的地表压强具有很好的一致性。经统计,二者均方根误差(RMSE)约为47.6 hPa,最大偏差不超过100 hPa。该偏差大于氧A波段反演理论误差的原因主要与DPC像元空间分辨率(3.3 km)较低有关,在这个较大范围内地表复杂的地形结构导致氧A带与DEM估算对应性之间存在较大的随机误差。但应该强调,两者结果很好的线性拟合相关系数说明了氧A带方法的有效性。

3.2 全球反演结果

图9展示了DPC/GF-5 2018年5月27日全球云顶压强反演结果。从图中可以看出:云覆盖了地球尤其是海洋的大部分区域,晴空多出现在干旱和内陆地区。低纬度和中纬度的云形状大多较碎;中高纬度的云多呈东西向的条带状,和地球风带有关;高纬度的云多呈块状。云顶压强较低即较高的云一般出现在低纬度的海陆交界区域附近,这是因为低纬度对流层高度较高,而中纬度和高纬度要低的多,限制了云顶高度。

图9 2018年5月27日DPC云顶压强全球反演结果样例。(a)DPC全球图像;(b)云顶压强反演结果Fig.9 The sample of DPC global retrieved cloud top pressure on May 27,2018.(a)DPC global image,(b)retrieved cloud top pressure

3.3 与MODIS云顶压强产品的对比

为了分析DPC云压强(基于氧气A带法)空间分布结果的反演性能,将DPC的云顶压强反演结果与MODIS云顶压强产品(基于CO2切片法)对比,比较二者的差异。

为去除DPC观测数据中的晴空、太阳耀光和冰雪等区域,在反演过程中增加一些简单的约束条件:1)要求海洋区域765 nm波段反射率大于0.08(大于该波段瑞利散射贡献反射率的最大强度);2)要求陆地和海陆交界区域443、565、670 nm反射率差值小于0.01(利用云像元可见光各波段反射率基本相等的特性);3)剔除南半球海洋区域反演压强大于950 hPa的像元(太阳耀光区域);4)剔除PDEM估算-P反演小于100 hPa的像元(冰雪覆盖区域)。考虑云的复杂三维结构,这里选择DPC观测天顶角最小的观测数据用于云顶压强反演。

选取MODIS/Aqua云顶压强产品(MYD06)作为对比数据。MODIS/Aqua与DPC/GF-5过境时间相近,均为当地时间13:30,可以保证云的位置、形状变化较小。MYD06云顶压强产品利用MODIS红外通道中第33～36波段通过CO2切片法反演得到,空间分辨率为5 km,对于卷云和中层水云其误差小于50 hPa,其他云误差小于200 hPa[25]。图10展示了DPC和MODIS在2018年5月27日的云顶压强对比结果。图中从上到下每行依次对应下垫面为:海洋(大西洋北部海域,纬度范围32°N～46°N,经度范围55°W～45°W)、沙漠(阿拉伯半岛附近,纬度范围18°N～32°N,经度范围50°E～60°E)、植被(美国与加拿大交界处,纬度范围40°N～54°N,经度范围110°W～100°W)。从图10可以看出,DPC云顶压强反演结果与MODIS产品的空间分布趋势具有较好的一致性。且DPC的云顶压强结果相比MODIS空间分布更为平滑,像元分辨率更高。此外,发现MODIS产品存在一些晴空像元的误反演现象[如图10(b)黑色方框所示,该区域明显为晴空海面,却反演出了“云顶压强”]和一些条带噪声现象[如图10(b)白色方框所示,这可能是由传感器探测元正反扫描响应差异、传感器机械运动等造成的[26]]。而DPC云顶压强结果则存在一些薄云和云边缘区域的漏反演现象,这是由于氧气A带算法对厚云适用性更好,在数据处理时采用了相对严格的云识别判据。

图10 2018年5月27日DPC和MODIS的云顶压强对比结果。(a)海洋区域;(b)沙漠区域;(c)植被区域Fig.10 Comparison of cloud top pressure between DPC and MODIS on May 27,2018.(a)Ocean region,(b)desert region,(c)vegetation region

进一步将DPC云顶压强反演结果与MODIS/Aqua云顶压强产品(MYD06)进行定量对比。由于MODIS云顶压强产品的空间分辨率为5 km,而DPC的空间分辨率3 km,为了尽量降低尺度因素的影响,同时避免边缘效应,选取大面积云目标的中间部分为样本区域,并对DPC与MODIS数据进行像元匹配。同时,选取的样本覆盖高云、中云和低云,以增加对比结果的代表性。

对比结果如图11所示,图中横坐标为MODIS产品的云顶压强,纵坐标为利用DPC氧气A波段观测反演得到的云顶压强。从图中样本横坐标可以看出,MODIS产品的压强值不连续,这是因为MODIS产品对压强做了近似处理(最小单位为5 hPa)。DPC和MODIS的云顶压强线性拟合斜率k=1.040,截距b=39.556,相关系数R=0.9567。这说明DPC反演结果与MODIS产品有很好的一致性。二者均方根误差(RMSE)约为98.6 hPa,其中大部分的DPC反演结果较MODIS偏高。此外,在云顶压强较低即云层较高时,二者偏差较大。可能是由不同算法(氧气A带算法和CO2切片算法)在低压强时敏感性不同,反演误差增大造成的。

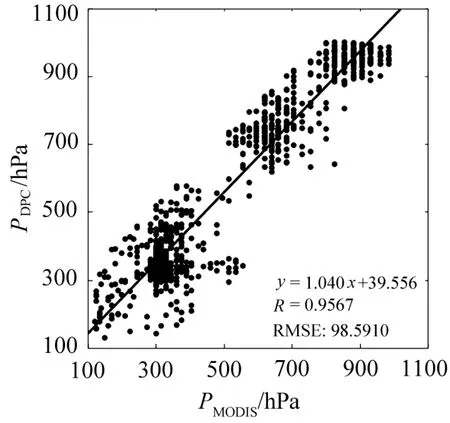
图11 DPC反演的云顶压强与MODIS云顶压强产品逐像元对比结果Fig.11 Pixel-by-pixel comparison between DPC retrieved cloud top pressure and MODIS cloud top pressure product

4 结论

基于DPC/GF-5的两个氧气A吸收波段(763 nm和765 nm,带宽分别为10 nm和40 nm),研究了云顶压强反演算法。首先,通过辐射传输模拟和多项式拟合得到了云顶压强和两波段表观反射率比值的经验关系,并对拟合公式进行了误差分析和校正,拟合公式整体误差小于1.5%。然后,分析了大气气溶胶、大气温压廓线等地气条件对反演结果的影响,结果表明这些因素对云顶压强反演结果影响均较小,可忽略。进一步利用DPC晴空地表观测数据,对反演方法进行了稳定性测试和原理性验证。稳定性测试结果表明该算法在不同太阳、观测角度条件下,反演结果差异在5%以内,具有较好的稳定性。晴空地表DPC反演的表面压强与DEM估算的压强对比的平均偏差约为47.6 hPa。最后,将DPC反演的云顶压强与MODIS云顶压强产品(MYD06)对比,结果表明二者有很好的一致性,云顶压强平均偏差约为98.6 hPa。

本反演方法理论上对于云和晴空地表均适用,云顶压强结果不但可用于云高估计,还可用于云识别和云分类。由于忽略云三维形状、云的透过及云层间多次散射的影响,本反演对于不透光且充满整个像元的厚云误差较小,约为几十hPa;而对于薄云或未充满整个像元的云边缘区和碎云则误差较大,反演结果相对真实值偏大。未来可通过增加氧A带光谱分辨率、传感器像元空间分辨率等途径进一步改进云顶压强产品的精度和适用性。