致密岩心带压渗吸规律实验研究

江 昀，许国庆，石 阳，余 玥，王天一，曾星航，郑 伟

(1.中国石油勘探开发研究院，北京 100083；2.中国石化 石油工程技术研究院，北京 100101；3 中国石油 西南油气田分公司，成都 610056)

鄂尔多斯盆地致密油藏孔隙度低(一般小于10%)、渗透率低(一般小于1×10-3μm2)、渗流通道小(发育大量微—纳米孔隙)、地层压力系数低(0.6～0.8)，目前虽已取得一定开发效果，但仍面临产量低、递减快和采收率低等难题[1]。目前，这类油藏提高开发效果的途径主要有2种：一是提高改造规模，采取大规模水平井分段压裂改造技术，将“万方水”注入后“打碎储层”，形成复杂缝网，缩短裂缝与基质渗流距离，达到增产改造的效果；二是压后闷井[2-5]，通过渗吸置换，提高驱油效率。尤其是渗吸置换作用，已被部分学者证实是一种有效提高页岩气藏/致密油藏采收率的方式[6-10]。

压后闷井过程中，大量压裂液通过滤失作用由裂缝进入基质，形成两相渗流区(图1)，分别是滤失作用(压差作用)主导且伴随渗吸作用(毛管力作用)的两相渗流区和渗吸作用主导的两相渗流区。

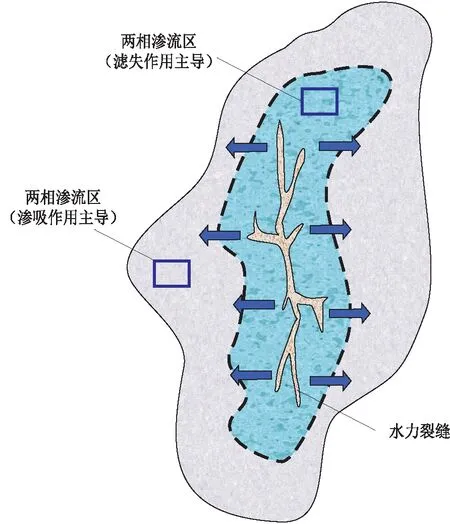
图1 压后闷井过程中两相渗流区域示意

渗吸作用主导的两相渗流区内，基质周围流体压力普遍高于孔隙压力，基质处于四周受压状态。取一微元(图2)进行分析，该微元在压差(ΔP，基质外部流体压力与孔隙压力的差值)作用下孔隙体积减小，并且在毛管力作用下发生渗吸置换(以逆向渗吸为例，Qw、Qo分别代表水相和油相流速)。

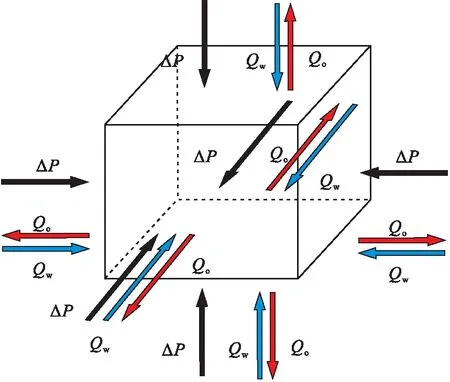
图2 渗吸作用主导的两相渗流区内压差作用下逆向渗吸示意

目前，致密岩心渗吸置换规律的实验研究主要集中于常压下渗吸置换(即自发渗吸)，并未考虑外部流体压力影响下的渗吸置换(即带压渗吸)。

对于致密岩心带压渗吸规律实验研究，存在以下几个问题：第一，岩心尺度的渗吸置换量少，且物理模拟实验在加压条件下进行，常规的体积法[11-12]和质量法[13-14]难以实现精确计量；第二，致密岩心在覆压条件下存在明显的应力敏感特征[15-17]，孔隙结构的变化是否会影响渗吸置换作用；第三，带压渗吸过程影响因素众多，实验结果能否进行归一化处理[18-22]，即能否建立带压渗吸无因次时间模型。

本文针对上述问题，首先，建立基于低场核磁共振测试技术的带压渗吸实验评价方法[23-26]，模拟压差作用下的渗吸置换过程；其次，测试致密岩心样品在覆压条件下孔径变化规律，结合自发/带压渗吸实验结果，分析二者异同点；最后，提出考虑压差作用影响的带压渗吸无因次时间模型，为确定压后闷井时间提供了新思路。

1 实验样品

1.1 岩心样品

致密砂岩样品取自鄂尔多斯盆地三叠系延长组主力开发层系长632小层，该井段为三角洲前缘—前三角洲沉积，以细粒长石岩屑砂岩和粗粉砂岩为主，全岩矿物包括长石(42.0%～53.3%)、石英(28.1%～33.9%)、白云石(11.0%～15.0%)以及黏土矿物(10.8%～17.2%)。黏土矿物主要由伊利石(9.2%～18.5%)、绿泥石(42.1%～60.6%)以及伊/蒙混层(25.2%～48.7%)组成。

岩心样品经过洗油(溶剂抽提法，30 d)，烘干(105 ℃密闭烘箱，48 h)处理后，测定其孔隙度(氦气孔隙度仪法)和渗透率(脉冲衰减法)。岩心样品分为3组(表1)。其中，第一组样品截取一段(A11-A15)用于高压压汞测试，其余部分(A21-A25)用于自发/带压渗吸测试，预先使用真空加压饱和装置对渗吸测试样品进行处理，即抽真空48 h后，在20 MPa压力下使用航空煤油饱和5 d之后，静置48 h，用于渗吸测试；第二组样品同样切为两段，分别用于接触角测试(B11-B13)和孔隙含油量标定测试(B21-B23)，用于孔隙油量标定的样品使用的饱和油方法与带压渗吸测试样品相同；第三组样品用于脉冲衰减测试(C1-C4)，确定不同有效应力下平均孔隙半径。

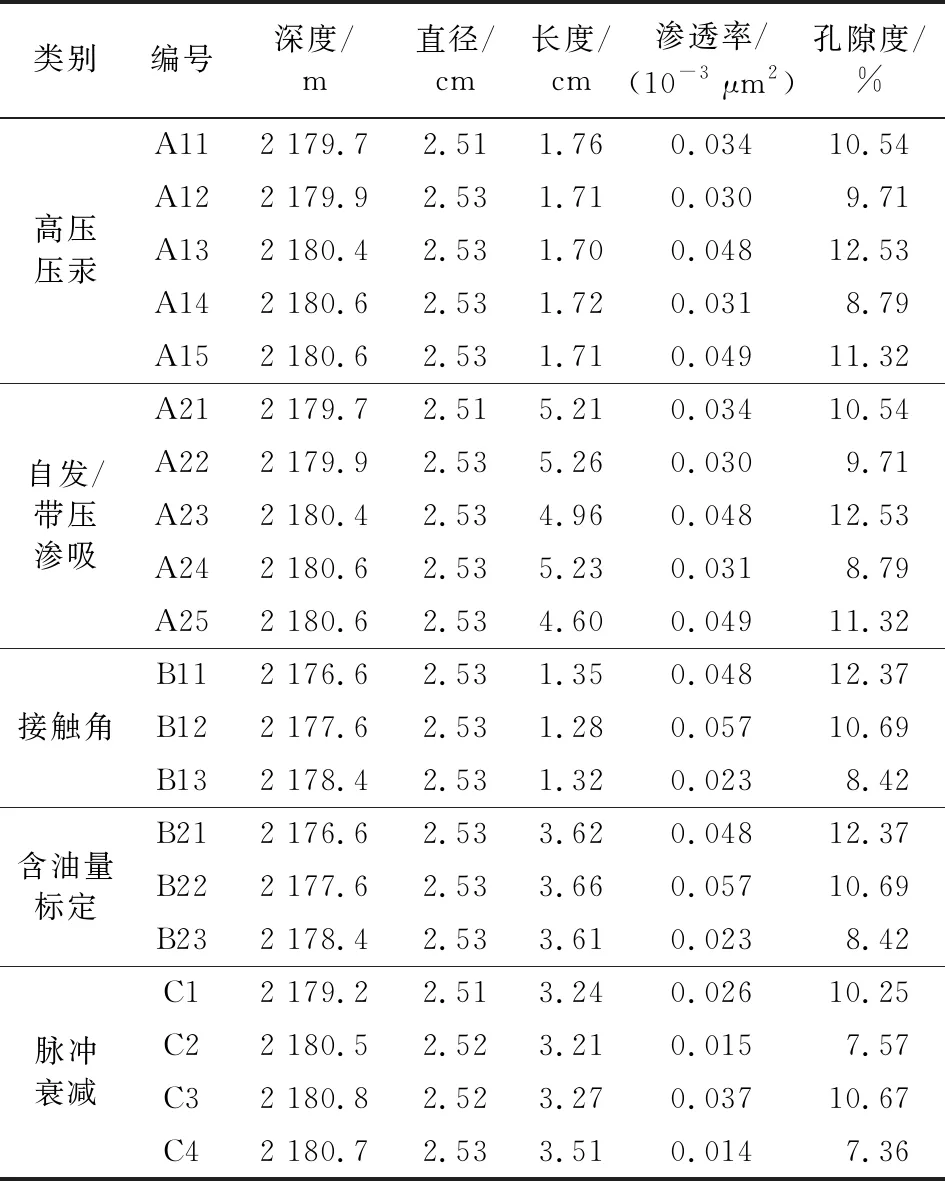
表1 带压渗吸实验岩心样品物性参数

1.2 流体样品

选用质量分数为2%～10%的氯化钾氘水溶液和3号航空煤油。其中，氘水(纯度99.9%)和航空煤油均购自实验材料供应商Cambridge Isotope Laboratories(表2)，氯化钾(纯度99.8%)购自国药集团化学试剂有限公司。

表2 带压渗吸实验流体样品物性参数(20 ℃, 1 atm)

2 实验方法

2.1 高压压汞

使用AutoPore IV 9520高压压汞仪测定岩心孔径分布信息，岩心测试前放置于200 ℃密闭烘箱中，持续24 h。孔隙直径根据Washburn方程[27]计算。

2.2 低场核磁共振

使用MesoMR-060H-HTHP-I低场核磁共振分析仪(磁场强度0.5 T)测定岩心核磁信号，测试采用CPMG(Carr，Purcell，Meiboom和Gill)脉冲序列，主要参数包括：回波时间0.3 ms，间隔时间3 000 ms，回波个数8 000，使用SIRT(联合迭代重建技术)反演算法得到T2谱。

在均匀分布磁场中，不考虑扩散弛豫和自由弛豫的影响(相比于表面弛豫的影响可忽略)，弛豫时间T2与孔隙半径可建立以下关系：

(1)

式中：T2为弛豫时间，ms；ρ为表面弛豫率，μm/s；S为岩心表面积，cm2；V为孔隙体积，cm3；R为孔隙半径，cm；C为常数，C=1，2，3，分别用于平板模型、毛细管束模型和球状模型，文中选用毛细管束模型，即C=2。

结合低场核磁与氮气吸附或者高压压汞测试结果，在相同条件下选取T2值与比表面或孔隙半径，可确定表面弛豫率。对于致密岩心，最常用的方法(平均值法)[28]是选取压汞法测试得到的平均孔隙半径和低场核磁测试得到的平均弛豫时间，按下式计算：

(2)

(3)

(4)

式中：T2LM为弛豫时间平均对数值，ms；Rp为平均孔隙半径，μm；T2i为第i点T2值，ms；Ai为第i点低场核磁共振信号幅值，a.u.；rj为第j点孔隙半径，μm；sj为第j点汞饱和度，%。

2.3 润湿性

使用DSA-100接触角测定仪，测试岩心接触角，确定其润湿性。实验步骤严格参照石油行业标准《油藏岩石润湿性测定方法：SY/T 5153—2017》。

2.4 孔隙含油量标定

建立T2谱累积积分面积(即累积信号幅值)与孔隙含油量换算关系，实验步骤如下：

(1)测试三块岩心(B21-B23)饱和油状态下T2谱；(2)将岩心置于CSC-12(S)超级岩心高速冷冻离心机中，分别在转速3 000～9 000 rpm下离心60 min(转速增幅1 000 rpm/次)，测试离心前后T2谱，并使用精密天平A&D GF-1000称量岩心样品质量；(3)计算给定转速下岩心样品离心前后T2谱累积信号量差值与离心前后质量差(即孔隙含油量)，构建孔隙含油量与T2谱累积信号幅值换算关系式。

2.5 自发/带压渗吸

开展自发/带压渗吸实验，模拟压差作用下的渗吸置换过程，实验步骤如下：

(1)测试岩心饱和油状态下T2谱；(2)将岩心与100 mL，2%KCl氘水溶液置于活塞式中间容器(图3)，打开中间容器上、下游的二通阀；(3)使用ISCO高压高精度泵以10 mL/min的恒定流速向中间容器底部持续注入蒸馏水，直到上游二通阀出液，将其关闭；(4)ISCO高压高精度泵切换至恒压模式，保持5个中间容器内压力分别为0，2.5，5，10，15 MPa(认为孔隙压力为0，中间容器内流体压力即为压差)；(5)每隔一段时间，取出岩心，使用棉纱擦干表面后，测定其T2谱；(6)重复步骤2～5，持续25天，直到实验结束；(7)将不同时间测试的T2谱累积信号幅值与岩心孔隙含油量进行换算，并按下式计算渗吸置换效率：

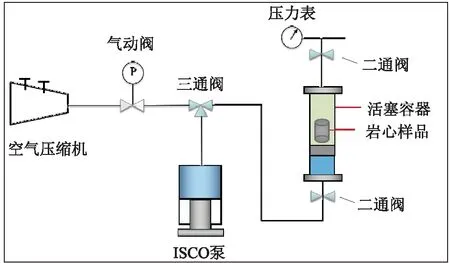
图3 自发/带压渗吸实验装置示意

(5)

式中：Roil为渗吸置换效率，%；m0为渗吸实验前岩心样品孔隙含油量，g；mi为第i次测试的岩心样品孔隙含油量，g。

2.6 脉冲衰减

使用PDP-200型脉冲衰减气体渗透率测量仪，测定岩心在不同有效应力(围压与上、下游压力平均值的差值，分别为0，2.5，5，10，15 MPa)下克氏渗透率(公式6)。

(6)

式中：ka为气测渗透率，10-3μm2；α为压力衰减半对数曲线斜率，MPa/s；μg为气体黏度，mPa·s；L为岩心长度，cm；cg为气体压缩系数，MPa-1；A为岩心截面积，cm2；Vu，Vd分别为上、下游腔体体积，mL；

参照KLINKENBERG[29]实验步骤，绘制气测渗透率和平均压力倒数关系曲线，根据拟合曲线的斜率和截距，并结合公式(7)～(9)计算克氏渗透率，以及相应的气体滑脱因子和平均孔隙半径。

(7)

(8)

(9)

式中：k∞为克氏渗透率，10-3μm2；b为气体滑脱因子，MPa；Pp为上、下游压力平均值，MPa；λ为气体分子平均自由程，μm；c为比例常数，等于1；r为平均孔隙半径，μm；Rg为气体常数，8.314 J/(K·mol)；T为绝对温度，K；M为气体分子摩尔质量，mol-1。

3 实验结果

3.1 孔径分布

高压压汞测试结果(图4a)显示，孔径分布主要集中在以下4个区间：1～10 nm，10～100 nm，100～1 000 nm，>1 000 nm。参照LOUCKS等[30]提出的孔隙尺寸分类方法，即孔隙类型分为纳米孔(小于1.0 μm)、微孔(1.0～62.5 μm)和中孔(62.5 μm～4.0 mm)三大类。可以看出，致密岩心孔隙类型主要为纳米孔(平均86.76%)和微孔(平均13.24%)。相应地，T2谱测试结果显示(图4b)，按T2值大小，孔径分布集中在以下4个区间：<0.1 ms，0.1～10 ms，10～100 ms，>100 ms。

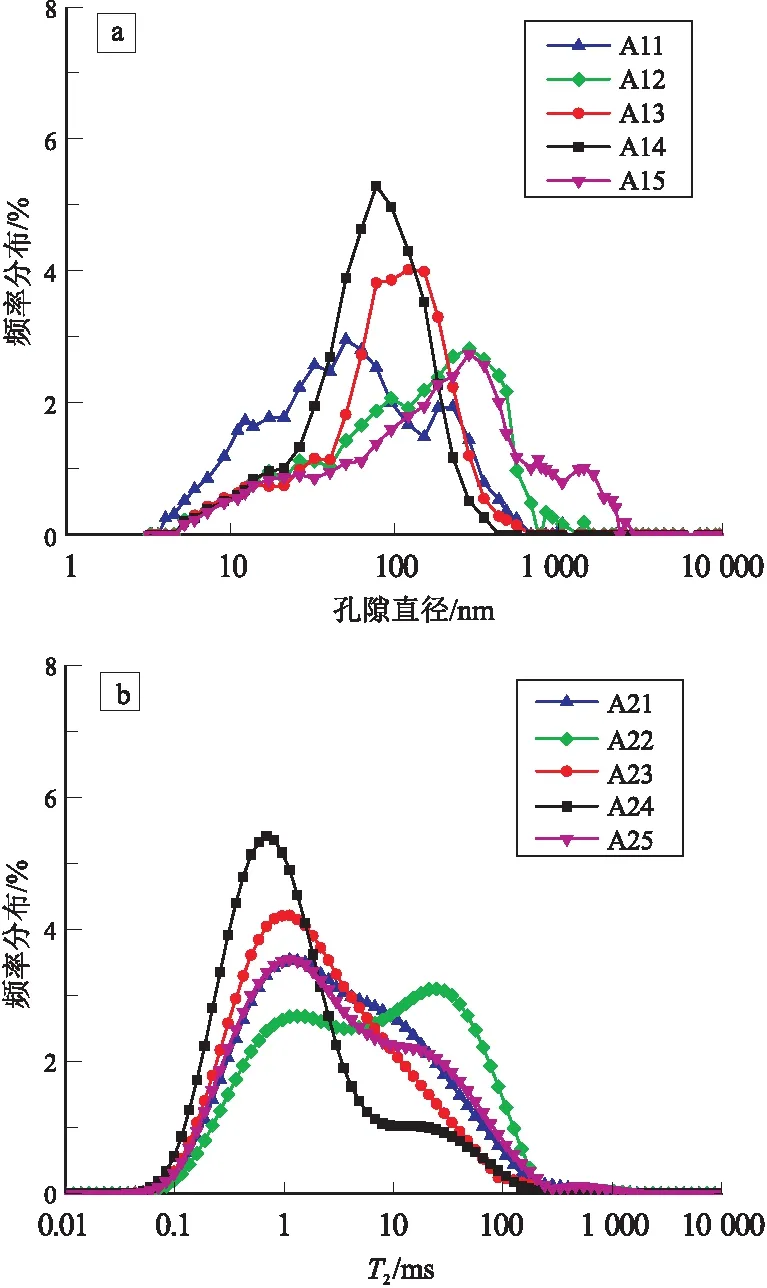
图4 高压压汞测试中孔隙直径分布结果 (a)

根据平均值法计算表面弛豫率(表3)，确定T2值与孔隙直径换算系数，并结合LOUCKS等提出的孔隙尺寸划分方法[30]，可以根据T2值大小，将孔隙类型进行分类(表4)。

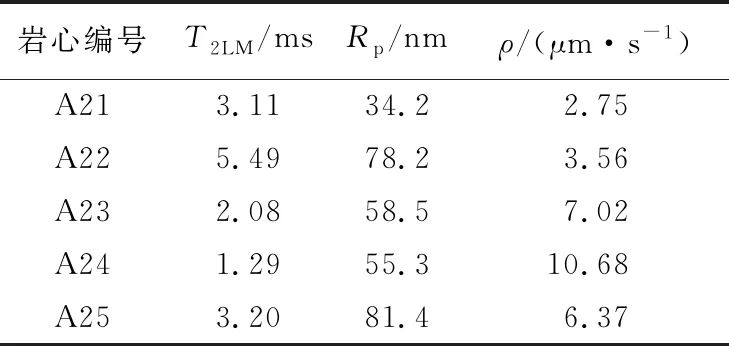
表3 平均值法表面弛豫率计算结果

表4 基于低场核磁T2值的孔隙类型分类

3.2 润湿性

根据TIAB等[31]提出的润湿性划分方法，接触角在0°至约60°～75°，系统为水湿；接触角在约105°～120°至180°，系统为油湿；接触角为75°至105°，系统为中性润湿。结果显示，岩心接触角分别为22.7°，27.7°和25.8°，表现为水湿。

3.3 孔隙含油量标定

T2谱累积信号幅值与孔隙含油量换算关系如下：

m=0.125∑Ai-0.301R2=0.954

(9)

式中：m为致密岩心孔隙含油量，g；ΣAi为T2谱累积信号幅值，a.u.。

3.4 自发/带压渗吸置换效率

自发/带压渗吸置换效率随时间变化关系曲线(图5a)分为2个阶段(分别用2条虚线表示)。渗吸初期，吸水量迅速增加，渗吸置换量及相应的渗吸置换效率均快速上升；之后，吸水量逐渐饱和，渗吸置换过程逐渐达到平衡状态，渗吸置换效率趋于稳定。随着压力的增加，渗吸置换效率随时间变化关系曲线中两条虚线交点(即快速上升阶段进入稳定阶段的转折点)处对应时间分别为15，10，7，5，3 d。类似地，渗吸置换效率随时间平方根变化关系曲线(图5b)也可分为2个阶段。第一阶段，带压渗吸置换效率与时间平方根呈幂指数关系，而自发渗吸置换效率则与时间平方根呈线性关系；第二阶段，自发/带压渗吸置换效率与时间平方根均呈线性关系。

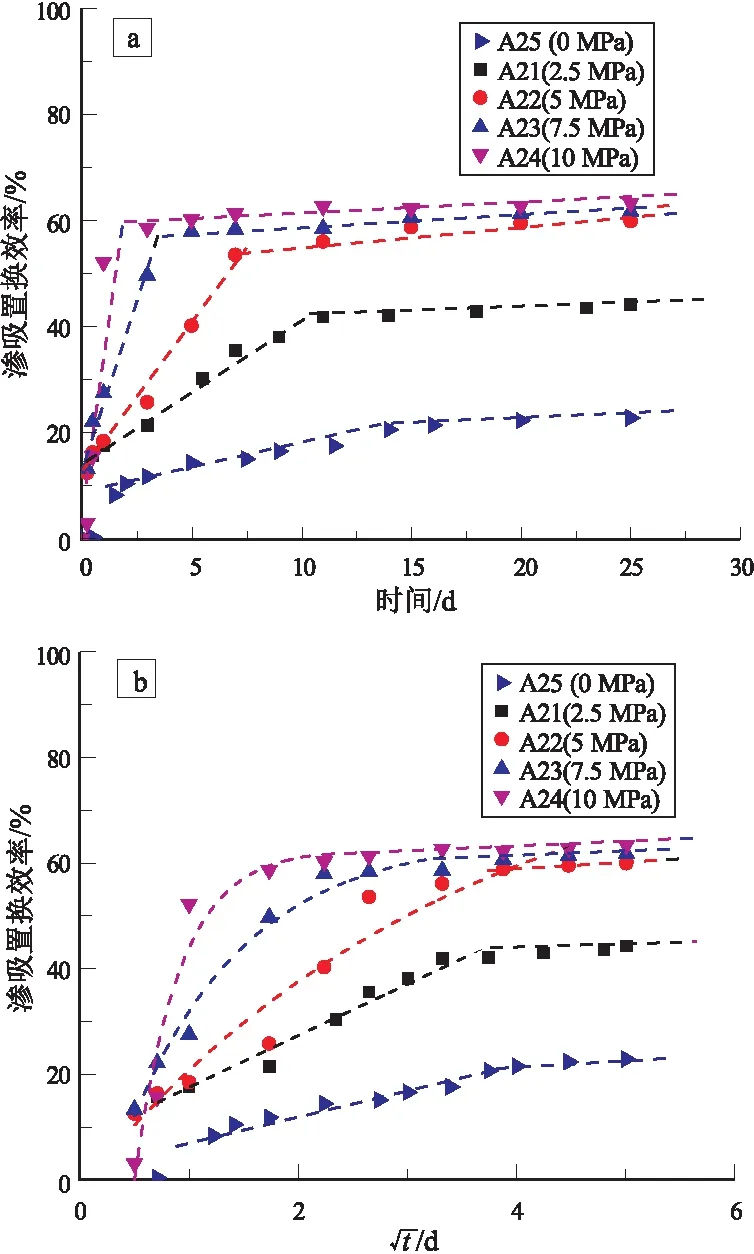
图5 自发/带压渗吸置换效率随时间(a)

同时，随着压力增加，最终渗吸置换效率分别为22.41%，44.41%，57.27%，61.84%，62.82%。并且，临界压力为5 MPa。

3.5 平均孔隙半径

根据脉冲衰减法确定气测渗透率，并计算相应的气体滑脱因子和平均孔隙半径(表5)。

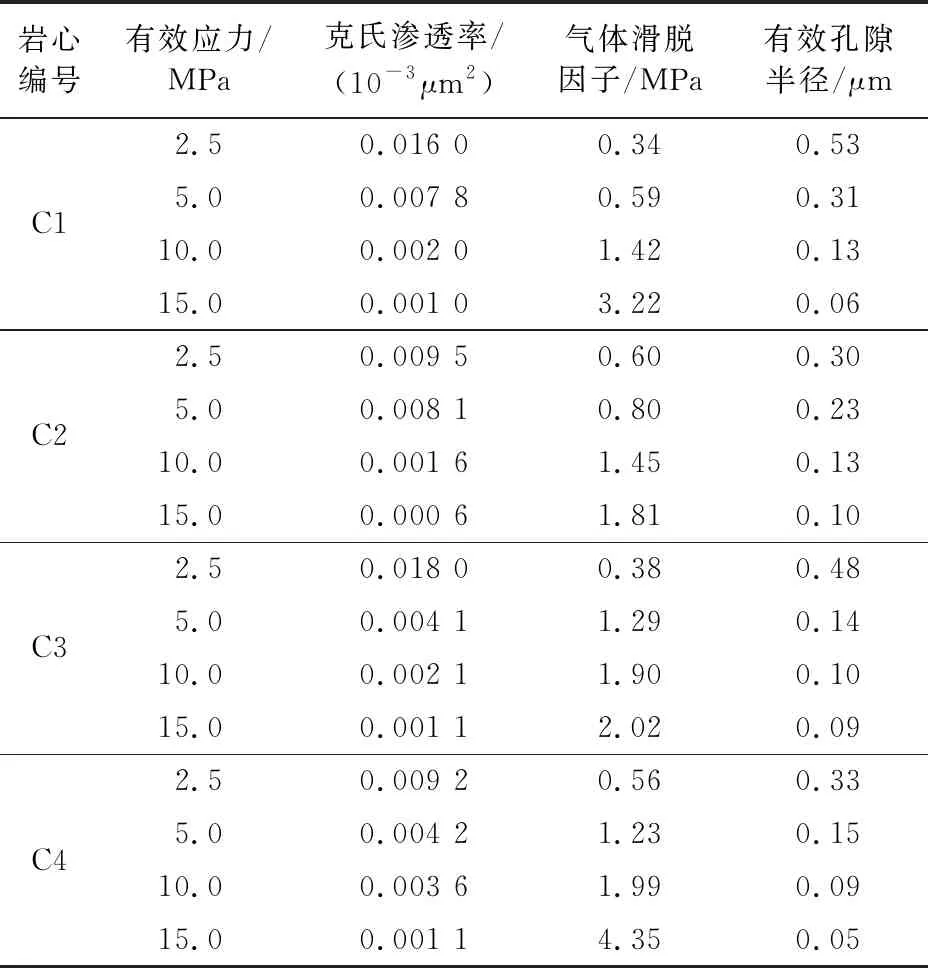
表5 气体滑脱因子与平均孔隙半径计算结果

结合平均孔隙半径计算结果，拟合得到平均孔隙半径随有效应力变化关系曲线(图6)。可知，有效应力小于5 MPa时，孔隙半径快速下降；有效应力大于5 MPa时，有效半径缓慢降低并逐渐趋于稳定。平均孔隙半径随有效应力变化关系由下式表达：

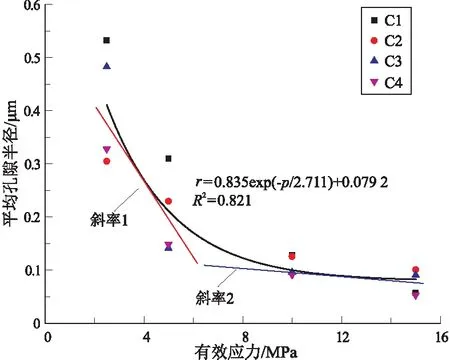
图6 有效孔隙半径随有效应力变化关系曲线

(10)

式中：r为平均孔隙半径，μm；P为有效应力，MPa。

4 结果讨论

4.1 微—纳米尺度孔隙内油相分布规律

T2谱反映了孔隙流体分布，根据饱和油岩心T2谱测试结果(图4b)可确定孔隙内油相分布规律。结果显示，质量分数为96.76%～97.25%的油集中分布于纳米孔(0.1 ms≤T2≤100 ms)内。为便于讨论，将纳米孔进一步划分为纳米微孔(0.1 ms≤T2<1 ms)，纳米中孔(1 ms≤T2<10 ms)和纳米大孔(10 ms ≤T2≤ 100 ms)。可知，这三类孔隙空间中，含油质量分数平均值分别为38.60%，37.64%，20.73%。

4.2 自发/带压渗吸对比

从以下三方面讨论自发/带压渗吸差异，即渗吸置换效率随渗吸时间变化规律、渗吸置换效率随时间平方根变化规律和微—纳米尺度孔隙内渗吸置换规律。

首先，自发/带压渗吸置换效率随时间变化关系曲线(图5a)均呈现两段线性增加的特征，存在临界压力，即当高于该压力时，最终渗吸置换效率趋于稳定。这一变化规律与致密岩心样品应力敏感特征(图6)一致。由毛管力计算公式(Pc=2σcosθ/r)可知，在界面张力和接触角不变条件下，孔隙半径随有效应力变化规律直接决定毛管力变化规律。因此，对于水湿岩心而言，带压渗吸过程的主要驱动力(毛管力)相比于自发渗吸过程会显著增加，提高吸水速率，可增加渗吸置换效率。这其中最重要原因就是平均孔隙半径减小引起毛管力显著增加，产生了强化的渗吸作用。

其次，自发/带压渗吸置换效率随渗吸时间平方根变化关系曲线(图5b)也可分为2个阶段。第一阶段，自发渗吸置换效率与时间平方根线性相关，但带压渗吸置换效率则与时间平方根呈幂指数关系，不再满足Washburn方程[27]；第二阶段，自发/带压渗吸置换效率与时间平方根均呈线性关系。可以推测，强化的渗吸作用并不是引起带压渗吸置换效率提高的唯一原因，压实作用同样发挥了重要作用，即在不同有效应力的作用下，由于孔隙体积压缩造成孔隙内部分油被挤出。但是，难以定量化表征强化的渗吸作用与压实作用分别对于带压渗吸置换效率的贡献，这是由于实验中只监测到油相信号，而非水相信号。后期研究中将考虑监测水相信号，进行定量化表征。因为渗吸作用会引起含水饱和度极大增加，而压实作用则不会引起含水饱和度的增加。

最后，根据T2谱特征，可分析渗吸置换过程中致密岩心孔隙内油相分布规律。图7a中5条曲线分别代表自发渗吸过程中测定的T2谱，2条曲线之间积分面积的差值反映了这段时间内渗吸置换量。图7b反映了自发渗吸前后纳米孔内油相分布比例。可知，自发渗吸在初期进行很快，并且主要发生在纳米孔(T2≤100 ms)内，当渗吸时间超过15 d后，渗吸过程进行缓慢，T2谱几乎不变(积分面积减少量小于3%)，即时间节点为15 d时测定的T2谱为临界曲线。自发渗吸实验前后，致密岩心样品中油相主要分布在纳米孔内，渗吸置换过程主要发生在纳米孔内，其中纳米中孔和纳米大孔内渗吸置换效率分别为6.88%和7.50%，而纳米微孔内渗吸置换效率较低，仅为3.07%。

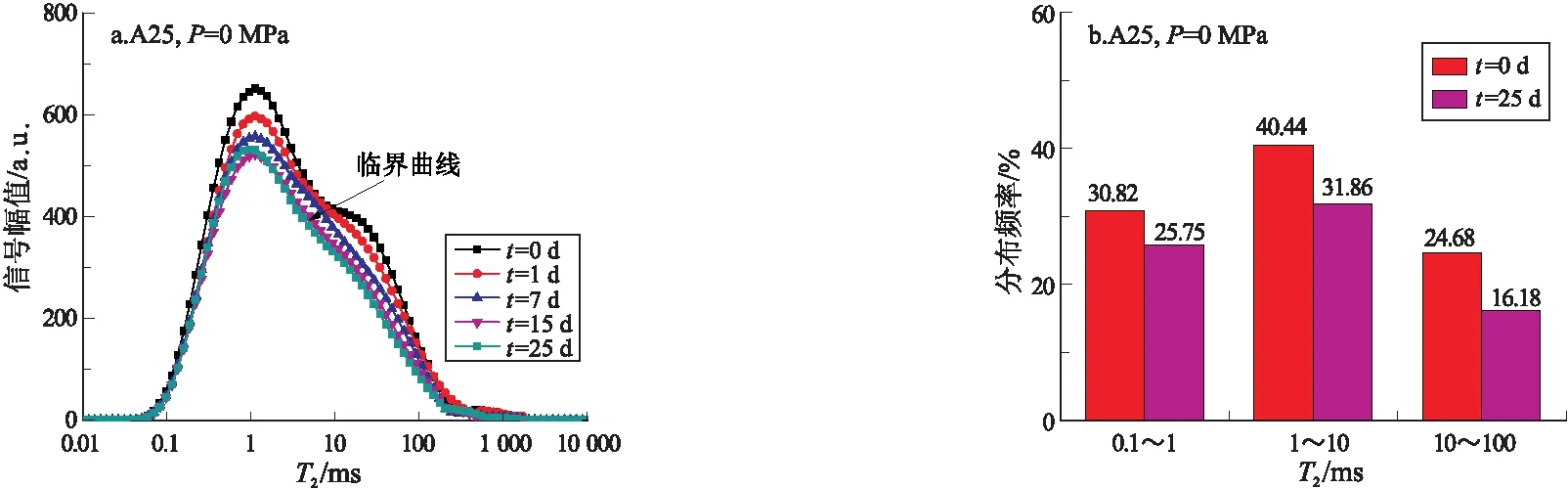
图7 自发渗吸T2谱及孔隙油相分布 (a) 和选定时间节点测定的T2谱渗吸实验前后纳米孔隙内油相分布(b)

相比之下，致密岩心带压渗吸置换过程进行更快(图8)，T2谱变化幅度更大，纳米孔内渗吸置换效率更高。当压力由2.5 MPa逐渐增加至15 MPa时，渗吸置换过程临界点处对应渗吸时间分别为10，7，5，3 d(图8a-d)；并且，带压渗吸过程中，纳米微孔、纳米中孔和纳米大孔内渗吸置换效率(图8e-h)平均值分别为20.54%，19.89%和14.46%。相比之下，自发渗吸过程中，这3类孔隙空间中渗吸置换效率分别为3.07%，6.88%和7.50%。因此，带压渗吸更易使得较小孔隙内发挥渗吸置换作用。

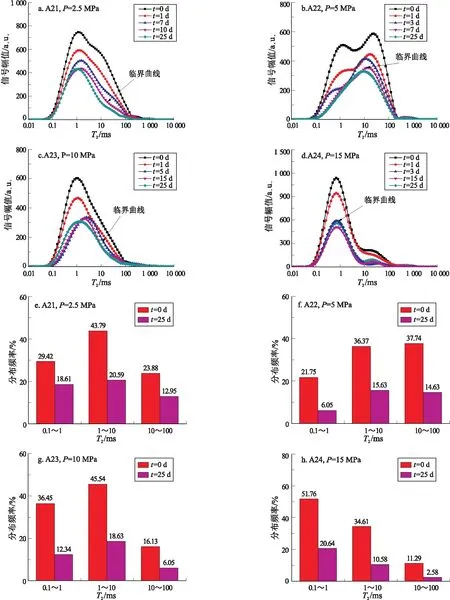
图8 带压渗吸T2谱及孔隙油相分布 (a-d) 和选定时间节点测定的T2谱渗吸实验前后纳米孔隙内油相分布(e-h)

相比于自发渗吸过程，带压渗吸过程的渗吸置换效率均大幅提升，纳米微孔、纳米中孔和纳米大孔内渗吸置换效率均有提升，尤其以纳米微孔和纳米中孔效果最显著。

4.3 带压渗吸无因次时间模型

影响渗吸作用参数较多(包括岩心样品形状、边界条件、润湿性和流体黏度等)，为了将带压渗吸实验结果进行归一化处理，便于将岩心尺度实验结果应用到油藏尺度，需建立归一化模型，有效对比不同岩心之间渗吸置换效率，间接预测油藏尺度开发指标，使得室内实验更具有应用价值，也为计算油藏尺度压后闷井时间提供参考。

将LEVERETT等[32]提出的毛细管束模型引入MASON等[21]提出的自发渗吸无因次时间模型，结合平均孔隙半径随有效应力变化规律，构建考虑压力影响的带压渗吸无因次时间模型，步骤如下：

(1)将毛细管束模型(公式11)引入自发渗吸无因次时间模型(公式12)

(11)

(12)

式中：tD为无因次时间；t为渗吸时间，s；ka为气测渗透率，10-3μm2；σ为油水两相间界面张力，mN/m2；φ为岩心孔隙度，%；μw为润湿性黏度，mPa·s；μo为非润湿性黏度，mPa·s；LC为特征长度，cm；

特征长度LC与岩心尺寸和边界条件有关，按下式计算：

(13)

式中：Vb为岩心基质体积，cm3；Ai为第i方向上渗吸接触面的面积，cm2；lAi为渗吸前缘沿开启面到封闭边界距离，cm；

(2)构建孔隙半径与有效应力函数关系式:

r=r(P)

(14)

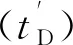
(15)

(16)

分别使用未考虑压力影响的MASON无因次时间模型和考虑压力影响的修正模型，得到不同压力下岩心渗吸置换效率随无因次时间变化关系曲线(图9)。

可知，渗吸置换效率随无因次时间变化关系曲线可分为2个阶段：(1)压力小于5 MPa，使用MASON模型和修正模型均能有效地将渗吸置换效率与无因次时间进行较好地拟合；(2)压力大于5 MPa，当无因次时间小于2 000时，使用MASON模型进行拟合则会产生较大误差，图9a中虚线区域各数据点发散，难以拟合。然而，使用修正模型进行拟合时，图9b中拟合曲线3能较好地将数据点拟合成功。因此，考虑压力影响后，修正的无因次时间模型是有效的。

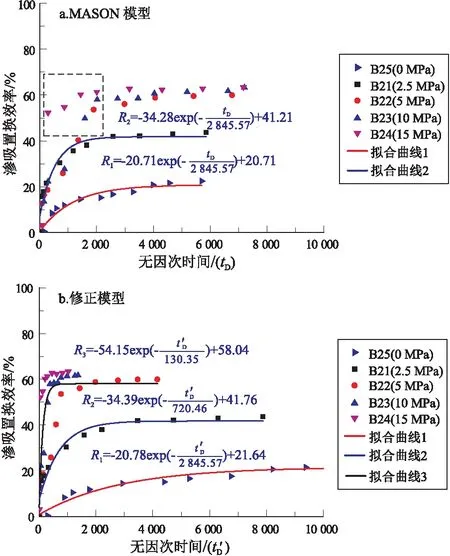
图9 渗吸置换效率随无因次时间变化关系曲线

借鉴LAN等[33]提出的自发渗吸数据归一化处理方法，基于岩心尺度建立的带压渗吸无因次模型，以渗吸置换效率达到最高为目标，提出了油藏尺度压后闷井时间计算思路，即根据岩心尺度和油藏尺度无因次时间相等原则，得到下式：

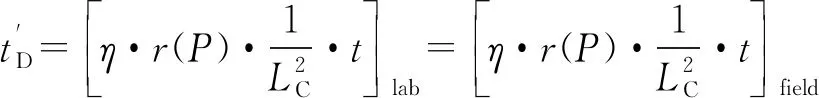
(17)

化简后，得到油藏尺度带压渗吸阶段持续时间(即闷井时间)计算公式：

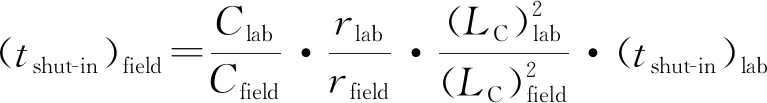
(18)

式中：Clab、Cfield分别为室内实验和油藏条件下特征系数；(LC)lab、(LC)field分别为室内实验和油藏条件下的特征长度；rlab、rfield分别为室内实验和油藏条件下的孔隙半径，依据室内岩心实验条件下有效应力(围压与进出口压力平均值的差值)与油藏条件下有效应力(上覆岩层压力与孔隙压力的差值)；(tshut-in)lab表示带压渗吸实验中，渗吸置换效率由快速上升阶段进入稳定阶段的时间。

5 结论

(1)纳米孔是致密岩心样品主要储集空间，质量分数为96.76%～97.25%的油分布在纳米孔内，其中，纳米微孔(0.1 ms≤T2<1 ms)、纳米中孔(1 ms≤T2<10 ms)和纳米大孔(10 ms≤T2≤100 ms)内含油质量分数分别为38.60%，37.64%和20.73%。

(2)压力由0 MPa逐渐增加至2.5，5，10，15 MPa，最终渗吸置换效率分别为22.41%，44.41%，57.27%，61.84%，62.82%。带压置换效率大幅提升是由强化的渗吸作用和压实作用共同造成的。

(3)考虑外部流体压力影响的带压渗吸无因次时间模型是行之有效的，这为确定油藏尺度压后闷井时间提供了思路。