基于极值copula和上尾copula的极端事件巨额损失统计推理研究

孟宜成

(淮南师范学院 金融与数学学院，安徽 淮南 232001)

0 引言

随着copula理论的发展，其应用范围已经扩展至经济领域，如信用风险分析、信用风险评级、资产组合风险、金融风险等[1].研究者利用copula理论与波动率相结合的方法总结出最小风险套期保值评估方法，并应用在部分现货或期货数据分析中[2].在金融保险业务中出现极端事件时，对于高额损失变量相关性的量化研究至关重要[3].然而，实际应用过程中往往会出现极端事件，虽然发生的概率较低，但也成为了金融保险风险管控中不可忽略的事件[4].例如，洪水、地震等自然灾害的发生对保险行业的考验是巨大的，这就需要引入极值理论对保险公司的损失进行数据拟合，即对一维随机变量的统计分析[5].如果将极值理论推广至多维随机变量的分析中，则可利用极值copula和上尾copula的极端事件巨额损失进行统计.本文基于copula函数拟合多维随机向量的联合分布，采用极值理论建立损失模型并对极值copula和上尾copula函数的随机向量进行统计分析.利用半参数预估方法对一般copula函数的参数进行预估并构建C-M(Cramer-Von Mises)统计量实现拟合优度的检验.

1 极值函数的定义

假定一个同分布独立d维随机向量Xi=(Xi1，…，Xid)′，将它的联合分布函数记为F，以CF表示其copula函数.

定义1假定C为一个任意的copula函数，在(u1，…，ud)′∈[0，1]d的条件下，如果有

那么C可定义为极值copula函数，CF即可定义为其吸收范围.相同条件下，如果

C(u1，…，ud)=(u1/n1，…u1/nd)n，

(1)

那么认为C处于最大稳定状态，同时可以断定，处于最大稳定状态的copula函数C必然在CF中.这种情况下，C为极值copula函数，且具有最大稳定性是必然的[4-5].

定义2若将式(1)视为一个渐进过程，则可将上尾copula函数定义为

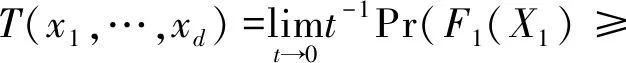
(2)

如果该式的极限值存在，则有(x1，…，xd)′∈(0，+∞)d.

上尾copula本质上并非copula函数，但其具有表达极限值的形式，在处理极端事件时，上尾copula相较于其它copula函数具有更好的稳定性.

定义3假设存在两个连续的随机变量X1、X2，F1、F2分别为其分布函数，则(X1，X2)的上尾相依系数表达式为

(3)

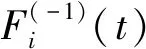
按照此定义，上尾相依系数描述了当随机变量大于某个分位数时，另一个随机变量也大于相应分位数的渐进概率.若设C为两个随机变量的copula函数，则(X1，X2)的上尾相依系数仅与C(t，t)有关，而C(t，t)作为[0，1]→[0，1]上的一个函数，可通过copula函数中的对角截面来描述.

定义4对于任意二维copula函数C，若

δC(t)=C(t，t)，则称δC：[0，1]→[0，1]为C的对角截面.

由此，可用δC(t)替代C(t，t)来表示上尾相依系数.不同copula函数具有不同的对角截面，所以在估计copula函数时可以通过对角截面的对比进行最优copula函数的选取.

2 一般copula函数的统计推断

实际应用中最常见的copula函数类包括Normal-copula、Student-copula、Clayton-copula、Frank-copula、Gumbel-copula、Plackett-copula等.对于这些一般copula函数，在确定参数θ后即可得到其具体表达形式，而函数的点预估可通过参数法、半参数法、非参数法三种方式进行.现有研究结果表明，半参数法不受限于边际分布，稳定性最强，因此本文采用半参数法进行点估计[6-8].

假设一个包含于参数族C(·;θ)的copula函数C，其连续密度函数为C(·;θ)，θ∈Θ⊂RP，采用半参数法进行函数拟合无需考虑边际分布，所以可以基于极大化的方式拟合对数似然函数，即

(4)

式中，

由此可获得函数的半参数预估结果

通过这一过程，能够实现相关数据的拟合，进而选出最优的copula函数,用以明确变量之间的相依关系.

利用半参数法得到参数的预估结果后，为了验证结果的准确性，本文基于拟合优度检验来证明copula函数C包含在参数族C(·;θ)之中，为此，提出如下假设检验.

H0:C(·)∈{C(·;θ):θ∈Θ}vsH1:C(·)∉{C(·;θ):θ∈Θ}.

(5)

通过构建C-M统计量，即能获得拟合优度结果：

式中，

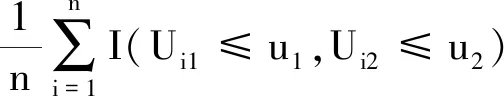
为二维似然copula.

3 极值copula函数的统计推断

3.1 常规的极值copula

二维极值copula的另外一种表达形式为

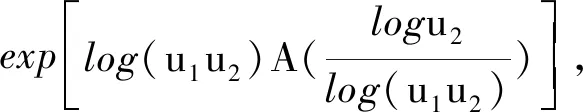
(6)

式中，A为[0，1]→[1/2，1]上的凸函数，即为Pickands相依函数.对于任意t∈[0，1]，max(t，1-t)≤A(t)≤1均成立.对于极值A(t)=1，则C(u，v)=uv，说明u与v是相互独立的；若A(t)=max(t，1-t)，则C(u，v)=min{u，v}，说明u与v是同单调增减的.

由此，只要设定相依函数A的具体形式，那么极值copula函数也会得以确定.应用最为广泛的极值copula函数主要包括：t-EV copula、Tawn-copula、 husler-copula、 calambos-copula、Gumber-copula[2].与一般copula函数相同，极值copula函数仍可利用极大似然法的半参数法进行点估计，而对于拟合优度的假设检验，则首先应结合经验数据对copula函数进行预估，再通过式(5)构建C-M统计量以计算似然copula与极值copula的差异.

3.2 上尾copula

依据定义2和定义3能够总结出上尾copula与其相依系数的关系.各种copule均具有其各自对应的上尾相依系数,应用较为广泛的几种copula函数的上尾相依系数如表1所列.

表1 常用copula函数的上尾相依系数

极值copula函数的上尾相依系数通过2(1-A(0.5))计算，即取决于其相依函数.

若设定(x1，x2)′∈(0，∞)2，由式(2)可以推导出上尾copula的似然函数为

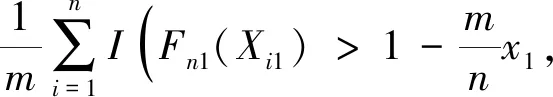
(7)

式中，m=m(n)→∞，且在n→∞的条件下m/n→0.根据前文所述，λU=T(1，1)，所以由式(7)可见Tn(1，1；m)可作为λU的一个预估值.

4 实例验证

选取国外某保险公司数据库中1980～1990年间自然灾害保险理赔的2167组案例数据作为研究对象，将其中losstobuilding和losstocontents两项作为本次研究的对象，将其分别记为两个损失随机变量X1(losstobuilding)、X2(losstotocontents)，其各自对应的分布函数分别记为F1、F2.本次研究以R软件为数据分析平台[8].

4.1 随机变量相关性

为了重点突出对极端事件下的高额损失的统计，本次研究选取赔偿额度在百万级以上的数据进行分析，共得到数据样本301组，其数值统计分析如表2所列.

表2 样本集数值统计分析

按照设定的数据分析目标，应对以下条件函数进行研究，

Pr(F1|≥1(X1)≤u1,F2|≥1(X2)≤u2).

上式中的(u1，u2)∈[0，1]2，Fi|>1(xi)=Pr(Xi≤xi|Xi≥1),i=1,2.

从理赔数据集中可以直接读取损失数据，这些数据及取其对数后的散点图如图1所示.

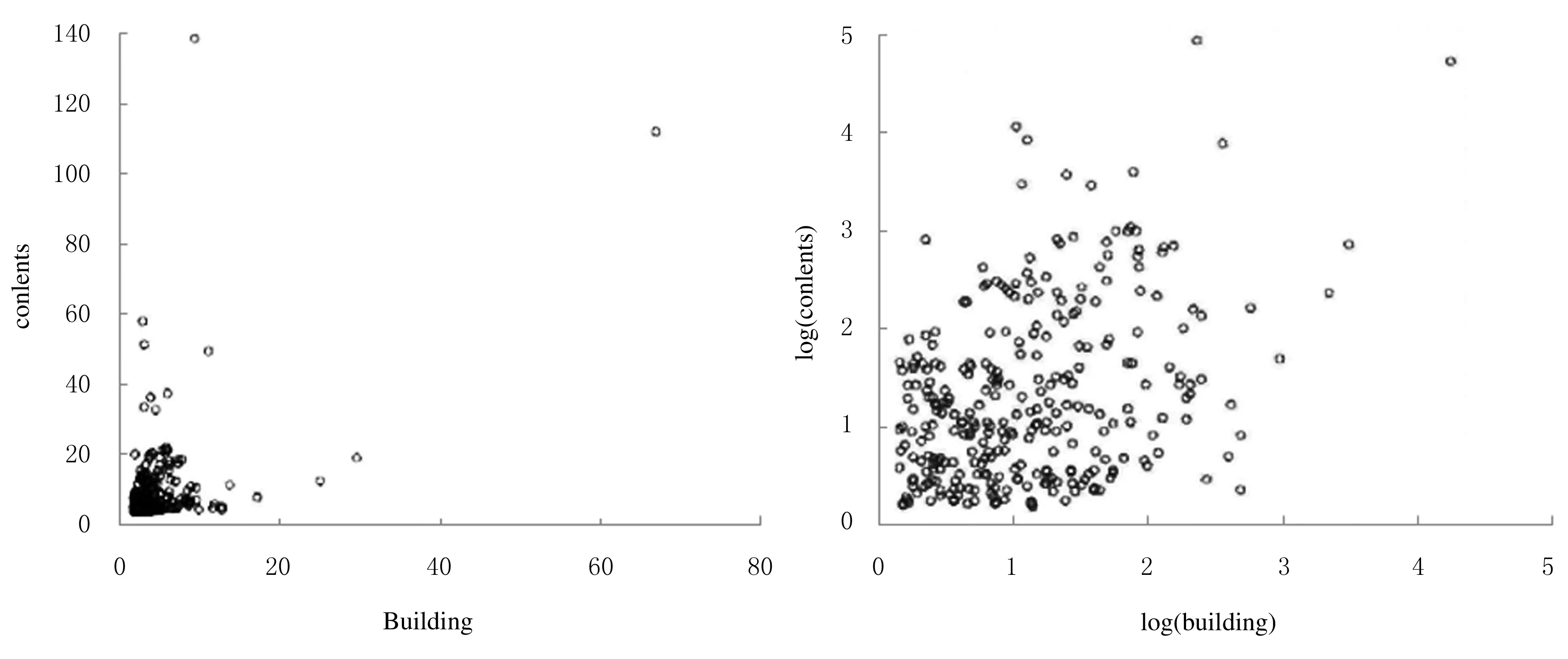
图1 损失数据及其对数化的散点图

由图1可见，X1与X2成正相关性关系.计算后可得到两个随机变量的Kendall秩相关系数值为0.211，Pearson相关系数值为0.512，由此验证了以上结论.

4.2 一般copula函数下的数据统计推断

由表3中的数据可见，对于p-值的计算，在设定置信水平为0.05的条件下，仅Normal-copula和Gumbel-copula接受了假设条件，但Gumbel-

表3 一般copula函数的半参数预估和假设检验结果

copula所得到的p-值更大.同时，用以描述似然copula与待选copula之间差异的C-M统计量值，Gumbel-copula所得到的结果最小.综合以上两点可以确定Gumbel-copula为所有待选函数中的最优函数.为了验证这一结论，分别绘制了似然copula、Gumbel-copula与Normal-copula的等高线对比图和对角截面对比图，具体如图2所示.

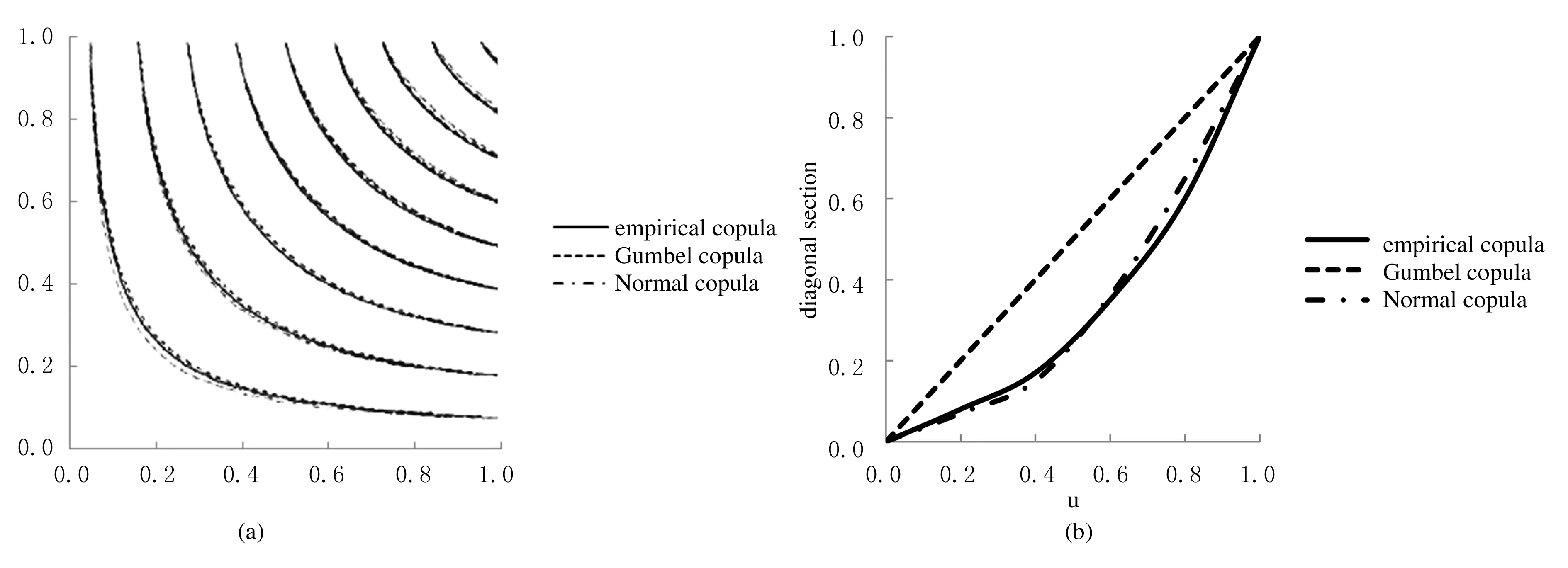
图2 3种copula的等高线与对角截面对比图

由图2可见，Gumbel-copula的等高线(左)和对角截面(右)与似然copula的对应曲线更为接近，从而验证了Gumbel-copula的最优性.

4.3 极值copula函数下的数据统计推断

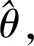
表4 极值copula函数的半参数预估和假设检验结果

由表4中的数据可见，对于p-值的计算，在设定置信水平为0.05的条件下进行拟合优度检验，除Tawn-copula外其它copula均接受了假设条件，而相比之下Gumbelcopula与Husler-Reisscopula所得到的p-值最大，进一步比较C-M统计量值，得出Gumbelcopula应为最优函数.

似然copula、Gumbel-copula与Husler-Reiss-copula的等高线对比图和对角截面对比图分别如图3(a)、(b)图所示.仅从图形上看，3种copula的等高线与对角截面都非常接近，难以准确验证Gumbel-copula与Husler-Reiss-copula哪个具有最优性，因此，需要确定式(7)中最合适的m值，以对上尾相依系数进行预估.不同m值对应的Tn(1，1；m)的函数图形如图4所示.

图3 3种极值copula的等高线与对角截面对比图

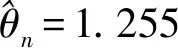
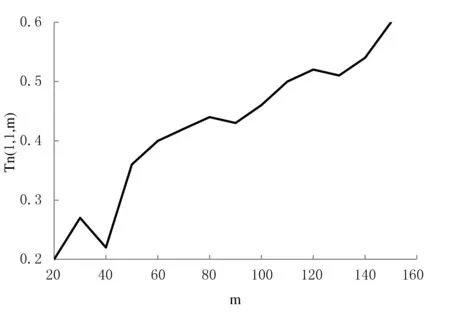
图4 不同m值所对应的Tn(1，1；m)

5 结语

为了明确极端事件发生时高额损失中各随机变量之间的相依关系，本文对极值copula与上尾copula进行了深度分析.首先介绍了copula函数的定义，然后将统计推断的方法由一般copula函数延伸至极值copula与上尾copula函数，最后通过实际案例对所研究的方法进行了验证，验证结果表明本文所提出的方法对于多维随机变量的相关性研究具有重要意义.