退化抛物型方程源项系数识别反问题
任如霞
(兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
一直以来,大家对经典抛物型方程的研究比较深入,而对退化模型的研究比较少.但是,由于实际问题的需要,特别是现代金融的发展,偏微分方程的退化越来越受到关注.例如,著名的Black-Scholes方程:
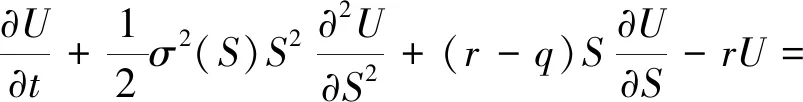
(1)
是期权定价的基本工具(见[1-4]),其中:U为期权价格;S为标的资产的价值;r为无风险利率;q为股票股利收益率;σ是波动函数.
可以看出,当S=0时,式(1)退化为常微分方程.
在一般的热传导方程中,系数识别问题已经被许多学者用不同的方法研究过.然而,很少有人考虑过退化的热传导方程.在这篇文章中,主要讨论了一个退化热传导方程的源项反演问题,即利用最终测量数据识别退化热传导方程中的源系数.这个问题可以用以下形式来表述.
问题P考虑以下二阶抛物型方程:
(2)
其中:a(x)、b(x)、c(x)和g(x)是已知的光滑函数,并且a(x)满足
a>0,a(0)=0,x∈(0,l);
方程(2)中的源项f(x)是未知的.
假设给出终端观测值作为附加条件,即
v|t=T=ψ(x),x∈(0,l),
(3)
其中T(T>0),ψ(x)是可以通过测量或者实验得到的已知函数.下面讨论如何根据(2)和(3)确定函数v(x,t)和f(x).
经典偏微分方程与退化偏微分方程的主要区别在于退化偏微分方程可能缺少边界条件,这也是退化逆问题的主要难点.对于方程(2),当x=0时,退化为一阶方程:
vt+b(0)vx+c(0)v=f(0).
事实上,根据著名的Fichera理论[5],可以很容易地得到在x=0的退化边界处,不应该给出边界条件.于是这里可以通过简单的计算看出抛物问题(2)是定义良好的函数.
首先将方程(2)第一个式子左右两边同时乘以-1,使得vxx的系数为正,即
-vt+a(x)vxx-b(x)vx-c(x)v=-f(x),(x,t)∈Q.
(4)
记x1=x,x2=t,有
a11=a(x),a12=a21=a22=0,b1=-b(x),b2=-1.
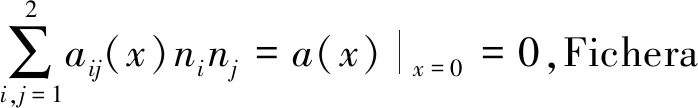
-b(x)-a′(x),
因此,要使左边界x=0处不必给出条件,由Fichera定理,只有Fichera函数的符号在该点处非负,即
(-b(x)-a′(x))|x=0≥0.
在文献[6]中,作者用变分迭代法研究了具有初边界条件的类似问题.在文献[2]中,作者采用Tikhonov正则化方法从终端测量数据中求解恢复方程
vt-∇·(a(x)∇v)=f(x,t),(x,t)∈Q
扩散系数a(x)的反演问题.
在文献[7-8]中,作者针对与时间和空间相关的q=q(x,t)进行研究,即确定下式中的未知系数q(x,t),
vt-Δv+q(x,t)v=0,(x,t)∈Q.
文献[9]主要研究了一个恢复退化抛物方程一阶系数的反问题,

其中k(x)满足以下退化条件:
k(x)>0,x∈(0,l),k(0)=k(l)=0.
最后,下列扩散方程中确定源项p(t)的反问题,

已经被许多学者所研究[10-14].
本文使用最优控制框架理论讨论问题P.证明了最优控制问题的整体适定性,这也是这篇文章的主要贡献.在第1部分中,进行了能量估计,以此来证明定解问题解的唯一性和稳定性.在第2部分中,将反问题P转化为最优控制问题P1,并构造了代价泛函最小值的存在性.第3部分给出了控制函数最小值的存在性和必要条件.第4部分证明了该极小化量的唯一性和稳定性.
1 能量估计
在文献[15]中,利用波动方程的能量模估计,得到定解问题解的唯一性与稳定性,这也同样适用于抛物型方程.
记QT={(x,t)|0 引理1[15](Gronwall不等式)若非负函数G(t)在[0,T]上连续可微,G(0)=0,且对于τ∈[0,T],有 其中:C>0为常数;F(τ)为[0,T]上不减的非负可积函数,则 G(τ)≤C-1(eCτ-1)F(τ). (5) 其中C是依赖于t的常数. 证明在(2)的抛物方程两边同乘v,并在Qt上积分,得 (6) 把式(6)左端第一部分的被积函数写成散度形式以便计算,得 (7) 式(6)左端第二部分采用同样的方法,有 (8) 根据已知条件有 由式(6)~(8),有 (9) 注意到 (10) 得到 (11) 对式(11)第二部分进行分部积分,有 (12) 根据a,b的光滑性,记 则式(12)可以写成 (13) 由Fichera条件,(a′+b)|x=0≤0,因此有 (14) 结合式(11)、(13)和(14)以及Gronwall不等式,有 定理证毕. 由于反问题P是不适定的,转而考虑以下最优控制问题P1: (15) 这里 (16) Α={f(x)|0<α≤f≤β,∇f∈L2(0,l)}. (17) 其中v(x,t;f)是方程(2)对应于给定系数f(x)∈Α的解,N是正则化参数,α,β是两个给定的正常数. 这里需要最终的观测结果ψ(x)满足: ψ(x)∈C[0,l]. (18) 假设c(x)的下界为c0,且c0为正常数.首先介绍两个基本定义和一些引理. 说明:在本文中,如果没有特别说明,C表示与T无关的不同常数. (19) v(x,0)=g(x),x∈(0,l), (20) 那么对于任意t∈(0,T],存在如下微分方程: (21) 引理2对于任何子序列{fn}∈Α,当n→∞,‖fn-f‖L1(0,l)→0,有 (22) 由于引理2的证明类似于文献[16],所以这里就不再作详细证明. 注意到J(fn)≤C,可以推断 ‖∇fn‖L2(0,l)≤C, (23) 这里C与n无关. 根据{fn}与式(23)的边界,得到 ‖fn‖H1(0,l)≤C. (24) 因此,选取一个{fn}的子序列,同样表示为{fn},使得 (25) 利用Sobolev嵌入定理,得 易看出{fn(x)}∈Α.因此,当n→∞时,在L1(0,l)中有 (26) 此外,根据式(25)有 (27) 由引理2和{fn}的收敛性知,存在一个{fn}的子序列,仍记为{fn},且满足 (28) 由式(26)~(28),有 (29) 因此, 定理得证. 定理3设f为最优控制问题(15)的解,对于任何h∈Α,存在一个三元函数(v,ξ;f)满足以下系统: (30) (31) 以及 (32) 证明对于任何h∈Α,δ∈[0,1],设 fδ≡(1-δ)f+hδ∈Α. 有 (33) 令vδ为方程(2)中f=fδ时的解,因为f是一个最优解,则 (34) (35) (36) 联立式(19)、(21),得到 (37) 定理1得证. 注1通过抛物型方程的共轭理论,可以得到该必要条件的另一种形式. 令Lξ=ξt-aξxx+bξx+cξ,且假设η是下面问题的解, (38) 其中L*是算子L的共轭算子. 根据式(37)、(38)得到 (39) 由式(39)和式(37),易得 (40) 与必要条件(37)相比,新得出的(40)不利于推导最小值的全局唯一性和稳定性.因此,本文在下一步讨论中仍将使用条件(37). 定理4假设ψ1(x)和ψ2(x)是两个给定的满足(18)的函数.设f1(x)和f2(x)分别为ψ1(x)与ψ2(x)对应的最优控制问题P1的最小值.如果存在一点x0∈[0,l],使得 f1(x0)=f2(x0), 有估计: 其中常数C仅与l和N有关. 证明在式(37)中,当f=f1时,令h=f2;当f=f2时,令h=f1,有 (41) 和 (42) 其中{vi,ξi}(i=1,2)分别为系统(30)与(31)的解,且f=fi(i=1,2). 设 V=v1-v2,Ξ=ξ1+ξ2, 则V,Ξ满足 (43) (44) 根据极值原理,知道式(44)只有零解,因此 ξ1(x,t)=-ξ2(x,t), (45) 且ξ1满足下式, (46) 注意到(43)、(46),有 V(x,t)=-ξ1(x,t). (47) 根据式(41)、(42)、(45)和(47),得到 (48) 由定理4的假设,以及Hölder不等式,对于0 (49) 从而得出 (50) 联立式(48)和(50),得到 (51) 定理4得证. 注2需要指出的是,正则化参数在不适定问题的数值模拟中发挥着重要的作用.由定理4可知,如果存在一个常数δ,使得 则 ‖f1-f2‖C(0,l)→0, 这说明重构的最优控制解是唯一且稳定的,与已有的结果一致[17].在实际计算中正则化参数N一般都取很小值,因此得到的是最优解的局部唯一性和稳定性.一般来说,对于不适定问题,正则化参数适当地依赖于数据误差趋近于零时,可以得到收敛结果.此外,在一些附加的假设下,也可以推导出收敛速度. 基于最优控制的框架,解决了下列退化热方程中重构源系数f(x)的逆问题P: vt-a(x)vxx+b(x)vx+c(x)v=f(x) 以及最小值的存在性、唯一性和稳定性也得以证明. 对于多维情况,本文提出的方法也同样适用.然而,由于多维域的几何复杂性及边界附近相应的简并,讨论过程可能比一维情况要困难得多,这也将是同仁今后的研究工作.
2 代价泛函的最小值存在性

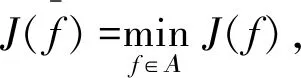

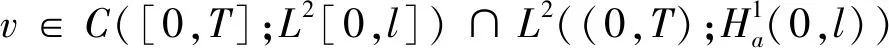




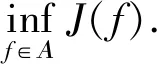
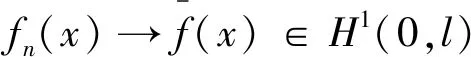

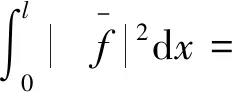



3 必要条件

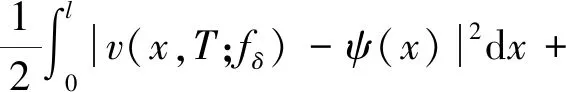
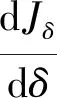
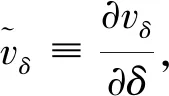
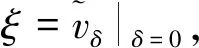

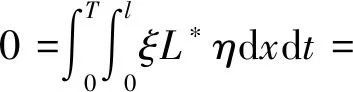
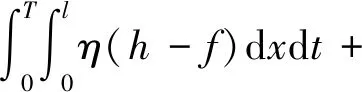
4 唯一性和稳定性




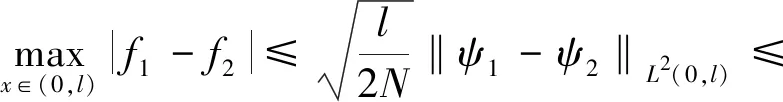
5 结语

