等差数列前n项和的一个递推关系式的丰富内涵
乌鲁木齐市高级中学(830011) 芦志新
定理设{an}是等差数列,Sn表示前n项和,则有递推关系式:
这个关系式定理具有丰富的内涵,主要表现在两个“推”上,即此定理递推关系式的多种“推导”方法所表现的深刻内涵和定理的多个“推论”之间的内在高度统一所展现的丰富性,使我们感到这个关系式定理的价值存在及其重要应用,下面就来一一说明.
一、定理推导方法多样性所表征的深刻内涵
推导方法一不妨设m > n,则有Sm −Sn=an+1+an+2+···+am=am+n),且因{an}是等差数列,则有an+1+am=a1+am+n.
(1)当a1+am+n=0 时,明显地有Sm −Sn=Sm+n=0,即
(2) 当a1+am+n ̸= 0 时,Sm −Sn=am)̸= 0,则有由对称性,当m 这个推导方法本身就是一种很好的证明方法,它融入了等差数列性质:若p+q=m+n,则ap+aq=am+an及当m > n时,有趣片段和关系式为Sm −Sn=an+1+an+2+···+am= 推导方法二由于{an}是等差数列,设其公差为d,则Sn=na1+· d,这说明数列 即证. 此推导方法用到了由{an}诱导出的另一个等差数列它的公差恰是等差数列{an}公差的一半. 推导方法三因{an}是等差数列,不妨设m ̸=n,则公差则 这个推导方法表征的意义为:两个等差数列{an}与之间有一致的递推关系,am+n=n)⇔ 推导方法四设等差数列{an}的前n项和为Sn,及m ̸=n,根据{an}前n项和Sn式子特点又可设为Sn=An2+Bn,则Sm=Am2+Bm,于是Sn −Sm=An2+Bn −(Am2+Bm) = (n −m)[A(m+n)+B],又m ̸=n,则A(m+n)+B=故有 这个推导方法用到了Sn的结构式Sn=An2+Bn及因式A(m+n)+B的整体结果,运算量小,是一种好的证明方法,体现了局部里的整体思想. 推导方法五(方程法)设m ̸=n,联立Sn=An2+Bn与Sm=Am2+Bm,解得:A=代入Sm+n=A(m+n)2+B(m+n) =(m+n)[A(m+n)+B]中有 此推导方法明显运算量较大,因为它是先利用方程组解参A、B,再回代A、B,可见推导方法四中利用先求因式A(m+n)+B的整体结果再回代,比推导方法五中解参再回代要好得多. 推导方法六设Sn=An2+Bn,则=An+B,等差数列的图像是一条直线上的点列,即有即证之. 推导方法七设Sn=An2+Bn,=An+B,设m ̸=n,有 此推导方法很直接,运用了Sn=An2+Bn和=An+B结构特点,且运算量很小. 推论一设{an}是等差数列,Sn表示前n项和,且Sm=Sn(m ̸=n),则Sm+n=0. 证明事实上,因Sm=Sn(m ̸=n),由定理知:=0(m ̸=n)得Sm+n=0. 推论一还有一种二次函数证法,可设二次函数f(x)=Ax2+Bx,若f(m)=f(n)(m ̸=n,即Sm=Sn),则其图象对称轴为x=故知f(m+n)=f(0)=0,有Sm+n=f(m+n)=0,即证之. 作为流行的练习题有:设Sn是等差数列{an}的前n项和,且Sp=Sq(p 推论二设{an}是等差数列,Sn表示前n项和,且Sn=m,Sm=n,则Sm+n=−(m+n). 证明事实上由定理知:即Sm+n=−(m+n). 作为流行的练习题有:(1)设Sn是等差数列{an}的前n项和,且S10=100,S100=10,则S110=____. (2) 设Sn是等差数列{an}的前n项和,且Sp=q,Sq=p(p ̸=q),则Sp+q=____. 推论三设{an}是等差数列,Sn表示前n项和,则S2n−1=(2n −1)an. 证明令m=n −1,由定理知:=an,即S2n−1=(2n −1)an. 推论三的内涵很丰富,an是a1,a2,…,a2n−1这2n −1个项的平均数,自然有S2n−1= (2n −1)an.此推论在平常的练习题和高考试题中应用较广,是一个很有价值的结论. 推论四设{an}是等差数列,Sn表示前n项和,则S3n=3(S2n −Sn)或S3n −S2n+Sn=2(S2n −Sn). 证明令m= 2n,由定理得即S3n=3(S2n −Sn)或S3n −S2n+Sn=2(S2n −Sn). 它的意义在于:等差数列的等距等长片段和还构成等差数列,即S(k+1)n −Skn=Sn+k(S2n −2Sn).这也是一个有价值的结论. 对于这四个推论,在以前我们没有发现它们之间有什么紧密的联系,但有了这个等差数列前n项和的递推关系定理,我们就知道了它们是高度统一的,这是自然赋予我们的一个多么神奇的事情啊. 推论五(进一步拓展)设{an}是等差数列,Sn表示前n项和,若p+q=m+n,则m ̸=n). 证明由定理得即证. 这是一个挺有意思的二级结论. 例1(2011年高考湖南卷理科第12 题)设Sn是等差数列{an}(n ∈N∗) 的前n项和,且a1= 1,a4= 7,则S9=____. 解析依题意,S1=a1= 1,S4== 16,由定理知(S4−S1) = 25,又得S9=9(S5−S4)=81. 注解S1=a1,当我们知道a1与am或a1+am的具体值时,就得到Sm(因Sm=),于是就可以多次用前述的等差数列前n项和递推关系式定理了. 例2(2013年高考全国课标Ⅰ卷理科第7 题)设等差数列{an}的前n项和为Sn,Sm−1=−2,Sm=0,Sm+1=3,则m=( ) A.3 B.4 C.5 D.6 解析由定理知0 =得S1=Sm−1=−2,于是得m=5,选C. 例3(2019年高考全国Ⅲ卷理科第14 题)记Sn为等差数列{an}的前n项和,a1̸=0,a2=3a1,则 解析依题意S1̸= 0,S2=a1+a2= 4a1= 4S1,由定理得S5= 25S1,同理得S8= 4(S5−S3) = 64S1.S10= 注解不论是给出等差数列两个项关系式、两个前几项和关系式还是一个项关系式与一个前几项和关系式,都可以列成关于a1(首项)与d(公差)的二元一次方程组形式,然后解之,再回代a1与d去求具体的第几项、通项、前几项和或前n项和等等,这是解决此类问题的通法.但通法有时计算量大、比较繁琐,必要时可看一下是否有符合前述定理的递推关系呢,如果有,那么在解题策略上就可选用上述例1∼例3 的方法了. 例4(2011年高考江西卷文科第5 题)设{an}为等差数列,公差d=−2,Sn为其前n项和,若S11=S10,则a1=( ) A.18 B.20 C.23 D.24 解析因S11=S10,由定理推论一知S21=0,又是等差数列,于是=a1+10d,则有a1=−10d=20,故选B. 例5(2018年高考上海卷第6 题)记等差数列{an}的前n项和为Sn,若a3=0,a6+a7=14,则S7=____. 解析由定理推论三知,S5= 5a3= 0,S12=a12) = 6(a6+a7) = 84,再由定理知:得+S5=14+0=14. 例6(2007年高考辽宁卷理科第4 题)设等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a7+a8+a9=( ) A.63 B.45 C.36 D.27 解析由定理推论四知,S9=3(S6−S3)=3·27=81,于是a7+a8+a9=S9−S6=45,故选B. 通过等差数列前n项和递推关系式定理及推论在高考试题中的应用,我们发现,解题方法是多样的,不断总结解题规律,找出问题间的联系,是通向深层次学习数学的必由之路,也是现今倡导提升数学素养的一种体现.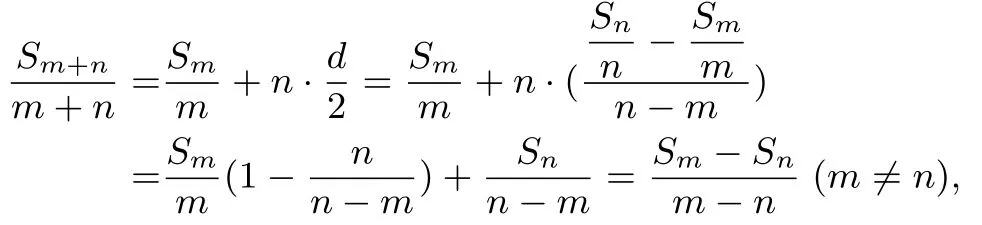



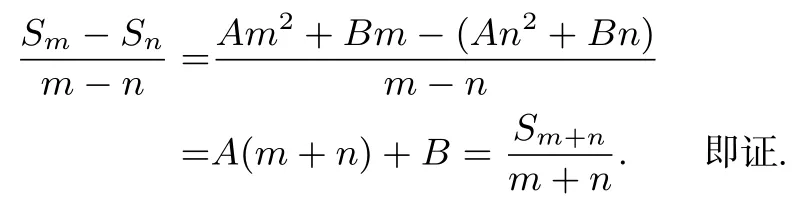
二、定理的丰富内涵
三、定理及其推论在解高考题中的运用

