在轨激励作用下低温推进剂动力学行为仿真研究

严 天 ，王 磊 ，2*，王娇娇 ，黄晓宁 ，马 原 ，2，厉彦忠 ，2

（1.西安交通大学制冷与低温工程系，西安 710049；2.航天低温推进剂技术国家重点实验室，北京 100028）

0 引言

在我国未来航天战略布局中，月球探测及其他深空探测将成为主要攻关方向[1]。深空探测任务的顺利开展要求火箭具备长时间在轨运行及变轨能力。低温液氢、液氧推进剂具有高比冲、无毒无污染等优点，将在探测中扮演重要角色。已有研究指出[2]，低温推进剂长期在轨存储与管理技术是未来航天任务发展的重要支撑技术之一。与常重力不同，在轨重力影响变弱时涉及多种弱力的综合作用，如气液黏性力、液体表面相对增强的张力等。因此在推进剂管理中，必须考虑低温推进剂在轨时的运行特性及规律。在轨期间，飞行器须完成的多次变轨、姿态调整和气液分离过程，表征为多种激励形式，包括轴向变过载、侧向激励、慢旋等。如不对推进剂行为加以控制，将导致贮箱底部管路口暴露，气体进入发动机，对飞行器的稳定产生不利影响。同时箱内液体晃动和气液相分布紊乱也不利于姿轨控制。因此，有必要对在轨状态下推进剂受激励后的动力学特性进行分析研究，掌握其规律，从而为推进剂管理设计及安全防护提供理论支撑。

对于推进剂晃动问题，国内外已有学者采用理论分析、数值模拟和实验测量等不同方法开展了相关研究。理论研究领域，Abramson[3]和Dodge[4]提出了用单摆和弹簧振子两种等效力学模型来分析容器内的流体晃动特征，并通过数学方法分析预测了流体动力学行为。在动力学数值分析方面，Himeno等[5]、Aoki等[6]、Yang等[7]和Beckman等[8]通过仿真方法证实了常重力下挡板对流体晃动具有抑制作用。Godderidge等[9]比较了实验和模拟结果的压力峰值，建议采用非均匀模型模拟剧烈晃动。Cheng等[10]提供了一种简化方法用于计算含挡板贮箱的动压特性。Shekari等[11]通过有限元分析发现，挡板高度、隔振基础的刚度等参数对最大流体动压和液体振动受力等有显著影响。Kargbo等[12]通过数值建模研究了分层晃动波特性，并按时间序列分别对界面下层和上层自由表面的液体晃动进行了快速傅里叶变换光谱分析，获得了流体层的能量和频率。Weidman[13]通过二维晃动特性模拟，研究了晃动频率随液体深度的变化规律。对推进剂晃动的热力学行为，也有学者开展了相关研究，Zuo等[14]关注了晃动过程中挡板对低温流体自增压及热分层的影响。Liu等[15-16]建立了一种非绝热氧箱模型，使用动网格捕捉气液界面运动，研究了液体初始温度、振荡幅度对贮箱压力分布、振荡力矩和界面动态响应的影响。实验研究方面，Konopka等[17]通过实验对比验证了一种与挡板等效的主动控制算法的有效性。Vairamani等[18]实验研究了磁场作用下半刚性结构膜对晃动的抑制效果。Pérez 等[19]、Himeno 等[5]、Aoki等[6]、Stephens 等[20]和Pridgen等[21]也开展了涉及推进剂晃动的实验研究，揭示了常重力下激励、液位高度及挡板参数对晃动过程的影响。目前对流体在外加激励下的研究主要针对常重力或大过载环境开展，对空间微重力下流体在外加激励下行为的实验研究相对不足。在实验研究方面，难以获得同时具备较长时间和较低加速度的微重力环境[22]，对激励发生时液面失稳乃至倾覆的事故，也鲜有实验数据作为支撑。

本文采用计算流体力学（CFD）软件FLOW-3D，以某型全尺寸Cassini等[23]低温贮箱为对象，构建可预测低温贮箱空间多种激励条件下流体行为的仿真模型。数值仿真空间微重力下初始倾斜界面、侧向正弦波、慢旋激励下箱内两相流体的运动特性，系统揭示微重力条件对流体行为演化规律的影响，并考核箱内设置防晃隔板对流体达到新平衡的作用效果。本文研究有助于理解空间低重力下低温贮箱内的流体运动规律，为低温上面级控制方案的设置、时序的优化提供理论指导。

1 模型建立

1.1 物理模型

图1展示的贮箱由一个直径为D，半径为R0，高度为h2的圆柱以及分别位于圆柱顶部和底部，高度为h1的椭球形封头组成。具体参数如表1所列。图1坐标系原点取为贮箱底部最低一点O，xyz轴向如图所示。液体充灌率为0.95，对应液位高度为H。箱内装有6组环形挡板，间隙为d。挡板用于抑制上升阶段液体的过量防晃。取挡板宽度为0.1D[5-6]。贮箱封头底部设有十字交叉挡板，用于防止底部液体塌陷。此外，图1展示了自由界面倾斜所产生的晃动，径向激励（文中将其简化为正弦函数），沿轴向的慢旋激励（文中将其简化为恒定角速度）的作用方向。图中标星号的位置坐标为（1.9 m，1.9 m，3.4 m），用于监测压力的变化。

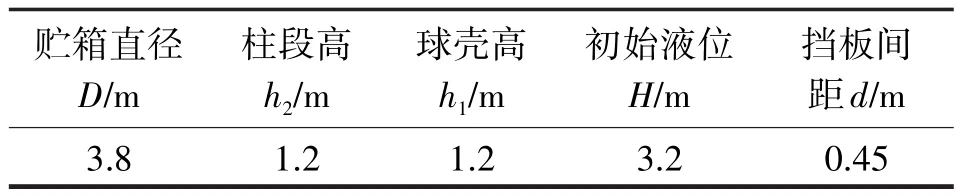
表1 贮箱参数Tab.1 The parameters of tank

图1 贮箱结构示意图Fig.1 The structure of tank

1.2 CFD模型

贮箱模型及网格如图2所示。在FLOW-3D中，先建立方形固体框架，再在中间挖出与贮箱等体积的空槽，通过对空槽的不同区域设置气液相，并导入挡板等固体结构实现建模。贮箱内所有的流体区域均被划分为尺寸一致的结构化网格。图中，深蓝色区域代表贮箱，内含流体区和挡板，由于两部分固体结构相互内切，图2（a）中模型只显示外侧箱壁，具体结构如图2（b）、（c）所示。

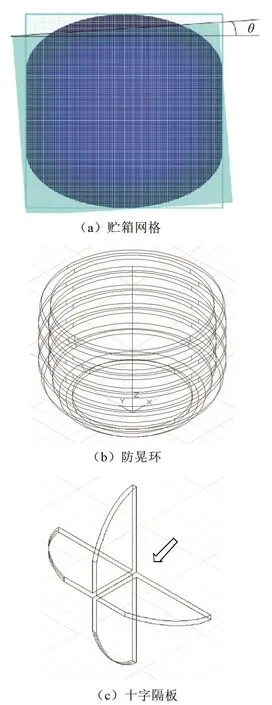
图2 网格模型及内部结构图Fig.2 The model of mesh and the internal structure

模型设置如表2所列。其中，采用RNG k-ε湍流模型，以准确描述近壁区的强剪切效应。在轨期间，为了实现气液相分离，满足供液与排气的需求，通常采用正推沉底发动机提供小过载正推，所产生的加速度约为10-3g0。火箭升空期间，不可避免地存在振动而引起箱内气液相晃动，当火箭入轨由大过载瞬变为微重力后，升空阶段的界面晃动可能对后期的两相演化产生影响。为此，本文将其简化为界面初始倾角机制，设置相界面与水平面夹角为θ，当不考虑该扰动作用时，θ=0°。空间低温贮箱常采用多层绝热（MLI）作为绝热手段，对应的壁面漏热在1 W/m2量级，在该漏热条件下，本文研究对象所产生的流体温升仅有3.3×10-6K，故可忽略壁面漏热影响。

2 模型校验

2.1 网格无关性校验

依照表2中参数设置，以液面倾斜4°为初始条件，对模型进行网格无关性验证，结果如图3所示。将网格数由5万逐渐增加至45万，对应网格尺寸从0.1 m减小至0.045 m，并与达平衡后气枕中监测点的压力进行比较。由图可见，网格数到30万后计算结果达到稳定。为了确保计算精度，以41万网格数模型开展后续的仿真计算。

表2 模型及初始参数设置Tab.2 The set of model and initial parameters

图3 网格数对仿真结果的影响曲线Tab.3 The effect of mesh on the simulation results

2.2 CFD模型校验

采用文献[5]报道的晃动实验校核本文所构建的CFD模型。该实验以水为工质，在常重力下展开，施加激励如图4所示。贮箱沿轴线（Z方向）受常重力加速度作用，沿径向（X方向）受外部正弦波激励作用，初始相位角为-180°，最大振幅为12 m；频率为1.47 Hz，振幅为5.32 m。过载加速度a与振幅A、频率ω的关系如式（1）所示：

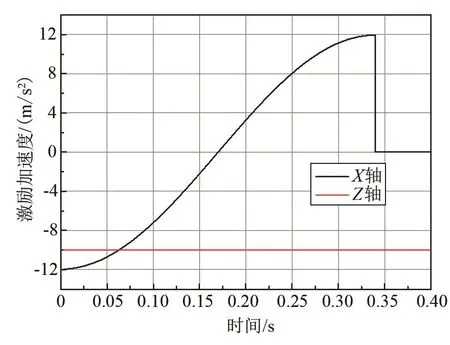
图4 施加激励的参数曲线Fig.4 The parameters of excitation

式中：t为时间；φ为相位角。

仿真结果与实验结果的对比如图5所示。可以看出，受激励后，实验贮箱和模拟贮箱内流体呈现相似行为，晃动的幅度和流体翻转、破碎等行为均相近，证实本文所构建的模型能够较精确地捕捉气液相界面的分布及动态规律，证明了该模型对激励工况下流体运动仿真的准确性。

图5 仿真结果与实验结果对比图Fig.5 Comparison of simulation results and experimental results

3 仿真结果与分析

3.1 倾斜液位下的晃动特性

为衡量晃动的剧烈程度，本文取Z轴质心位移开展特性研究，质心由式（2）得到。定义液氧全部位于贮箱顶部与液氧全部位于底部对应的质心差为所允许的最大晃动幅度，为15.0 cm。本文以实际的质心变化范围相较于最大幅值的比值进行分析。

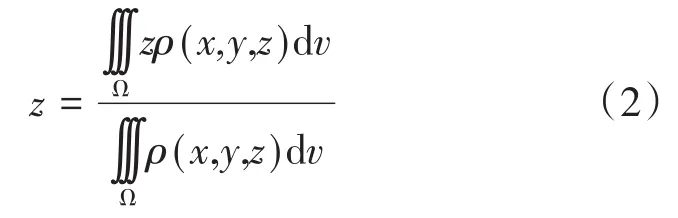
式中：z为质心垂直方向坐标，m；Ω为体积，m3；ρ为流体密度，kg·m-3。

图6（a）、（b）、（c）分别展示了10-3g0下液氧初始倾斜角度θ分别为1°、3°、5°时的质心位移演化曲线。其中，横坐标为计算时间100 s，纵坐标为有无挡板时质心晃动幅度占最大值的百分比。结果表明，在液位恢复稳定的过程中，质心做振幅衰减的周期性波动，并逐渐接近平衡。这是因为在微重力下，晃动时产生的湍流黏性耗散发挥作用，在分子黏性作用下动能转化为热能，液面逐渐静止，趋于水平。

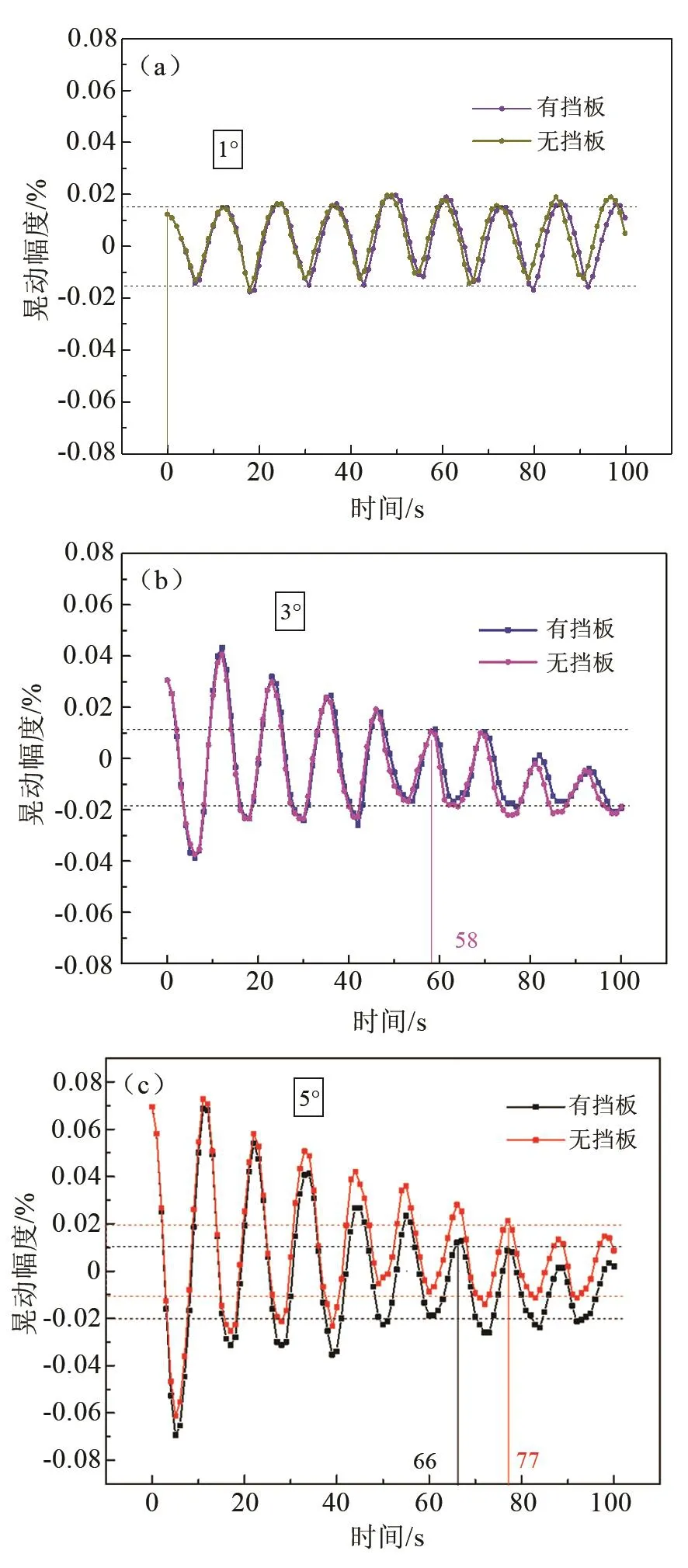
图6 10-3g0下不同液面倾角下防晃效果对比曲线Fig.6 Comparison of anti-slosh effects under different liquid inclinations under 10-3g0

实际过程中，气液界面晃动自初始状态到完全稳定耗时较长。为便于分析，本文以质心晃动幅值5×10-3cm（约占最大幅值的0.033%）作为达到稳定的评判标准。取达到该标准的第一个波峰对应时间作为稳定的时间。对比发现，当初始液位倾角较小时（θ=1°与θ=3°），箱内挡板对相界面晃动的抑制作用可忽略，而当θ=5°时，挡板在微重力下会加速液面从倾斜到水平的过渡速度，达到平衡的时间从77 s降到66 s，缩短了14.3%。此外，θ=1°工况下气液界面的晃动处于较低水平，质心近似呈现等幅振荡；θ=3°工况下晃动幅值可见明显的衰减；而在θ=5°工况下晃动幅度大幅降低的同时，防晃隔板的作用凸显。对比结果表明，箱内气液相分布可在流体黏性耗散与防晃隔板两种作用下达到新平衡。当初始气液界面倾角较大时，晃动引起的惯性冲击也相对较大，防晃隔板可有效抑制晃动幅值，加速其平复速率；而当初始倾角较小时，惯性冲击力作用微弱，流体主要在黏性力作用下达到新的平衡，故防晃隔板作用微弱。

取液面初始倾角 5°，分别计算 10-3g0、10-4g0、10-5g0微重力工况下有挡板贮箱内的晃动特性，结果如图7所示。可以看出，随着重力水平的降低，箱内流体晃动周期显著延长，且所能达到的最大质心波动幅值也有所降低。重力越小，晃动周期越长，黏性耗散作用对晃动的抑制效果相应减小，故达到新的平衡位置需要更长时间。

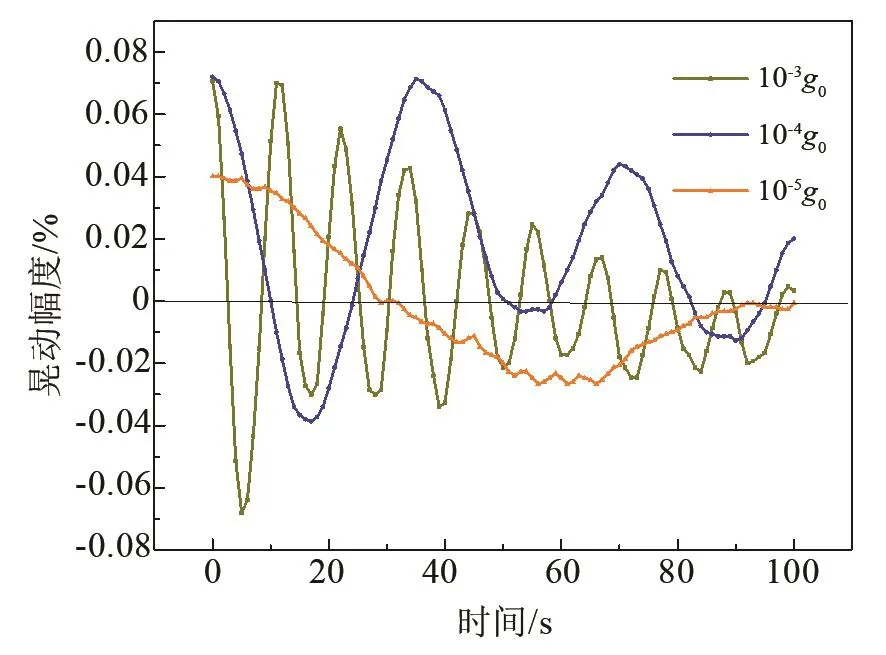
图7 不同重力环境下液位倾斜后质心演化曲线Fig.7 Evolution curve of centroid with liquid inclinations under different gravity environments

3.2 小过载侧向激励下的防晃特性

上面级运行时，燃料系统可能受到来自贮箱侧向的激励，对箱内的流体行为产生影响。为研究该激励的特性，设激励为作用于Y轴方向，频率为0.144 Hz的径向简谐波。参考以往研究[24-26]，简谐激励的振幅一般取贮箱直径的0.05～0.4倍。分别研究振幅为0.1 m、0.2 m、0.3 m的对应情况。10-3g0环境下，2.6 m、3.2 m液氧液位工况对应的质心演化规律如图8（a）、（b）所示。

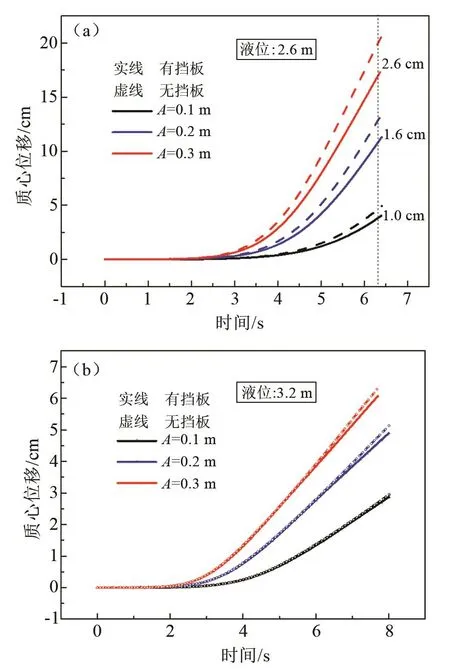
图8 微重力下不同液位不同径向正弦激励防晃效果对比曲线Fig.8 Comparison of anti-slosh effects of different liquid levels and different lateral sinusoidal excitations under microgravity

由图8可知：（1）激励振幅越大，质心向上偏移的量越大，晃动越剧烈。图中展示的时长约为一个周期，按设想质心曲线应呈往复趋势，但由于液体质量很大，惯性也很大，受激励后将立即向初始方向运动，不易向反方向运动，因此质心持续升高。而且激励波的能量与振幅的平方成正比。振幅越大，波的能量越高，传递给推进剂的能量越高，转化的位势能越大，质心位置也越高。（2）比较图8（a）、（b），发现挡板效果随液位不同呈明显差异。这是因为，当液位低于挡板时，液体的速度可分为两部分，一部分平行于挡板表面，使其沿激励作用方向运动，但不引起Z轴质心变化；另一部分垂直于挡板表面，使其做轴向运动。结合无挡板时液体质心运动趋势，垂直方向的速度分量所占比例较大。在发生向上的位移过程中，流体运动被防晃板阻挡，故图（a）中挡板效果显著。当振幅为0.3 m时，可抑制质心偏移量达到2.6 cm；当液位高于挡板时，上部的液体不受挡板约束，运动随意性较大，挡板对该部分流体几乎不起作用，故图（b）中抑制效果微弱，振幅为0.3 m时，质心偏移最大仅为0.3 cm。

为衡量挡板防晃效率，定义挡板效率为η，该值越大，表明挡板防晃效果越好。

挡板效率随液位变化如图9所示，该图表明，当液位低于挡板最高位置时，挡板能发挥良好效果，效率较高。防晃效率与高度呈近似线性关系，重力越大，下降速率越快。10-3g0微重力下挡板效率曲线的降低速率比常重力更平缓，这意味着在半满箱或更高液位时，挡板在轨阶段仍能发挥一定的防晃作用。

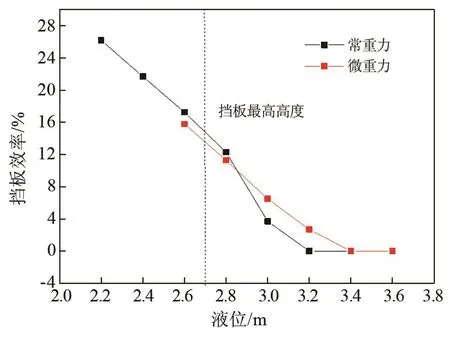
图9 不同重力环境下挡板防晃作用效果随液位变化对比曲线Fig.9 Comparison curve of the baffle anti-slosh effect of different liquid levels under variablet gravity

图10展示了图8（b）计算周期内贮箱压力及气液相分布。贮箱内空白空间为气枕区。液体颜色代表压力水平，液体压力由蓝至红递增。由图可知，在小过载下，贮箱内先出现压力分层，压力与液位深度成正比，底部液压最大；之后，激励传来，气枕沿着壁被传送。不难推测，若以此趋势继续晃动，或振幅加大，气枕将被传送至底部输液管口，造成输液管含气，再被输至发动机将产生不利影响。因此在实际微重力工况下，应避免径向激励所产生的过量气液位置偏移。

图10 振幅为0.2 m时不同时刻贮箱压力的分布对比图Fig.10 Comparison of the distribution of tank pressure at different times when the amplitude is 0.2 m

3.3 空间慢旋下的防晃特性

为研究挡板对液体慢旋状态的影响，将自旋角速度分别设置为0.1 rad/s、0.3 rad/s、0.5 rad/s，获得10-3g0时液氧达到稳态的气液相界面分布，如图11所示。随着角速度的增大，液面内凹程度加深，压力分布趋于均匀，中央气体区呈近锥形，锥的高度逐渐增大，底圆直径减小。这是由于气液两相间存在较大的密度差，旋转时液相受惯性离心力更大，会被甩离轴心更远，但受贮箱壁阻挡，表现为液位上升。当角速度大到一定程度，不难想象，气锥将与底部相接。

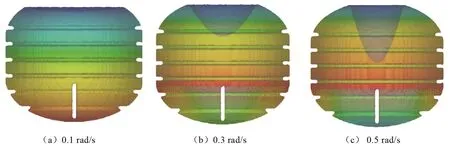
图11 贮箱轴向慢旋时的气液相分布对比图Fig.11 Comparison of gas and liquid phase distribution of tank during slow axial rotation

质心演变曲线如图12所示。图（a）中注明了贮箱内质心平衡位置。0.1 rad/s、0.3 rad/s工况的平衡位置相差0.65 cm，0.3 rad/s、0.5 rad/s工况的平衡位置相差1 cm。从达到平衡的时间上看，角速度越大，质心波动越大，达到平衡的时间越长。0.5 rad/s时挡板的效果对比如图12（b）所示，从质心波动幅度判断，有无挡板差异很小，即挡板使贮箱液体被抬高，质心位置更高。但挡板存在与否几乎不影响流场达到稳定建立平衡的时间。这是因为挡板主要对流体沿Z方向的位移起抑制作用，而该情况下流体受径向的离心力为主，速度方向也与挡板作用平面平行，故防晃作用微弱。

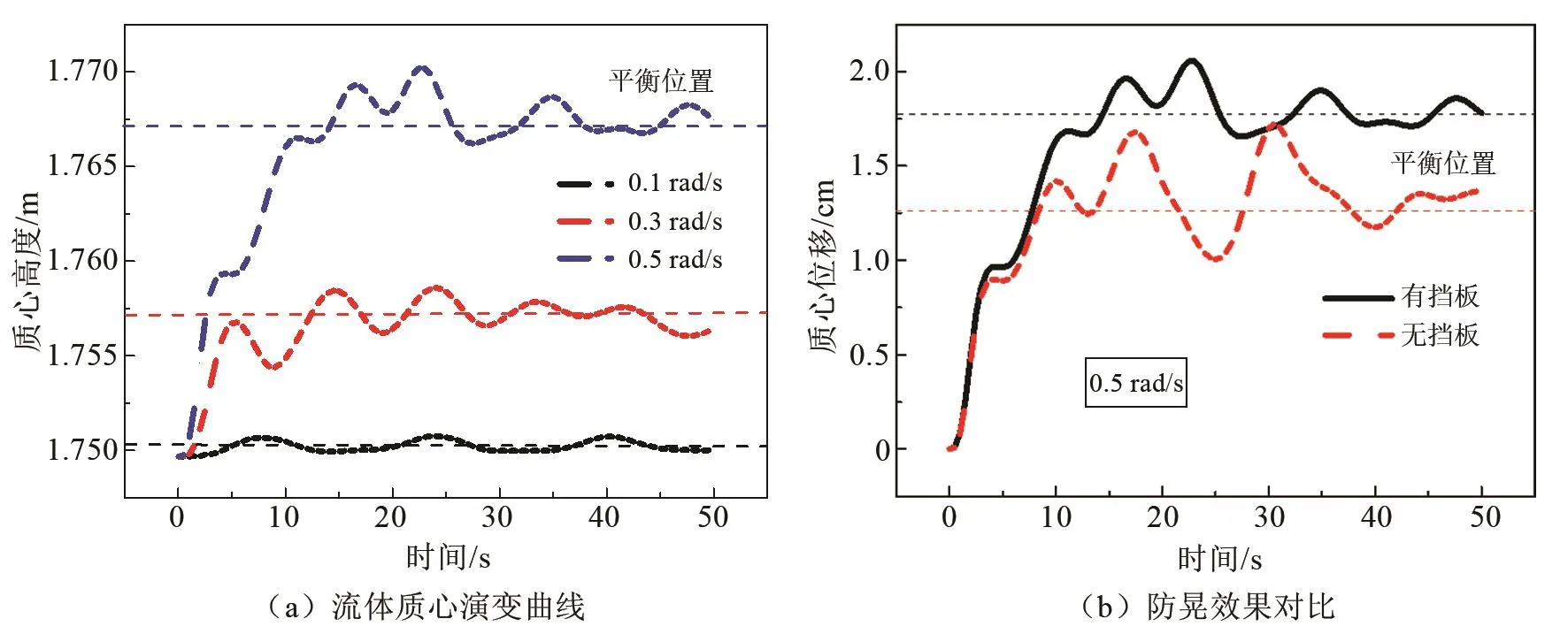
图12 流体质心演变曲线及防晃效果对比曲线Fig.12 Evolution curve of fluid centroid and comparison of anti-slosh effect

综上，沿轴线的角速度有利于贮箱内实现快速气液分离，而旋转引起的尖细气锥有可能接触箱底，对气体进入输液管造成不利影响。因此有必要根据贮箱含气率、分离完成要求等指标设计相应角速度。

3.4 防晃挡板对不同推进剂贮箱流体晃动的影响

上述结果基于液氧工质开展。而实际应用中，液氢/液氧往往成对出现。氢的密度、黏性力均比氧更小，因此，在地面激励下，氢比氧需要更长的稳定时间。在微重力下，重力的影响被削弱，为研究氢氧行为的差异性，用液氢替代液氧开展仿真研究，并比较两种工质在不同激励下的规律差异。

当液位倾斜时，3.1节结果已表明，工质自由振荡具有明显的周期性。本文Cassini贮箱内液体自由振荡的周期由式（4）[19]计算：

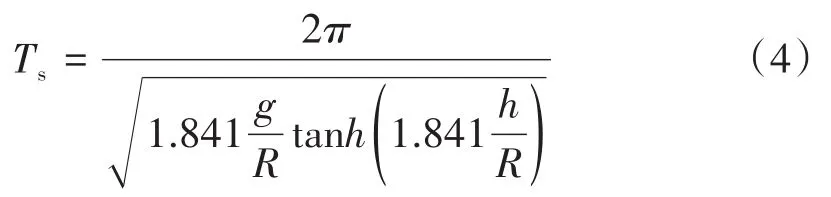
式中各符号意义见1.1节，R为贮箱半径。设θ=4°，计算氢氧工质的振荡周期，为直观观察规律，取周期对数值为纵坐标，重力对数值为横坐标，作图如图13所示，红色虚线为氢氧振荡趋势线。

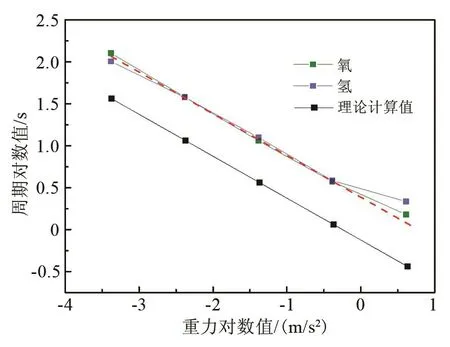
图13 液位倾斜时氢、氧晃动周期对比曲线Fig.13 Comparison of hydrogen and oxygen slosh periods with liquid inclination

由图可知，在本文考虑的重力范围内，氢氧周期十分相近，但与理论计算值有一定差距。这是由于理论计算公式中未考虑挡板的存在，故当把理论公式应用于文中贮箱时，应加以修正。由图中红色虚线可得到重力范围[10-5g0，10-1g0]内的简化关系式如下：

经校验，该式误差不超过3.38%。

径向激励下流体类型对有挡板贮箱的影响如图14所示，贮箱初始液位为3.2 m。图中氢氧行为呈现较大差异。氢的振荡幅度为6.5 cm，占最大允许值的43.3%，氧为4.0 cm，占最大允许值的16.0%。前面结果已表明，液位高于挡板时，液体晃动抑制效果较弱，结果表明，由于物性差异，氢的运动范围远大于氧。因此，对于径向激励工况，防晃效果与推进剂类型相关，应优先关注液氢的防晃，如加高氢箱内的挡板高度等。

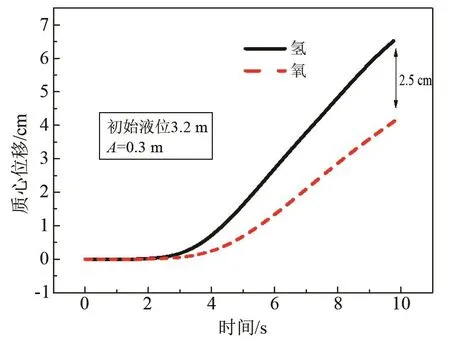
图14 径向正弦激励下氢、氧质心演化对比曲线Fig.14 Comparison of the evolution of hydrogen and oxygen centroids under lateral sinusoidal excitation

在有挡板贮箱慢旋情况下，氢、氧两流体行为如图15所示。从质心演化曲线看，氢氧平衡位置几乎等高，相较于贮箱尺寸，差异可忽略不计。因此对于慢旋工况，可不考虑氢氧箱内流体行为的差异。

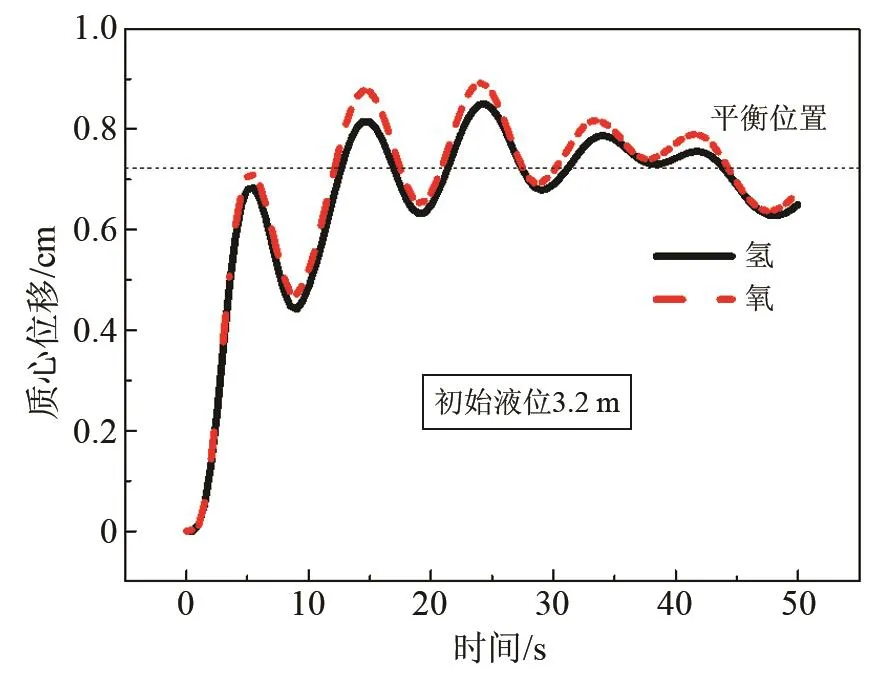
图15 慢旋下氢、氧质心演化对比曲线Fig.15 Comparison of the evolution of hydrogen and oxygen centroids under slow rotation

4 结论

本文采用CFD方法，就贮箱在空间中受多种激励后的低温推进剂流体运动特性开展了仿真研究，包括初始液位倾斜、径正弦波、慢旋激励等工况，并讨论了防晃挡板的作用，结论如下：

（1）防晃挡板的作用效果受初始液位倾角大小影响，当倾角较小时，由于流体晃动的惯性冲击较低，防晃挡板未见明显的作用；而当初始倾角较高时，挡板可使相界面加速恢复稳定。当过载从常重力瞬变为微重力后，倾斜液面达到动力平衡耗时约80 s。

（2）本文用有无挡板时流体质心变化量的比值来描述流体的晃动演化规律。贮箱经历径向激励后，若液位处于挡板附近高度，则常、微重力下防晃挡板均能抑制晃动，且效果与液位近似成线性关系。液位越低，防晃效果越佳。同一激励作用下，2.6 m液位工况时抑制的幅度约为2.6 cm，而3.2 m液位仅对应0.3 cm。

（3）箱内流体在径向激励作用后的晃动特性与其类型相关。同一激励下，氢的质心晃动范围可达6.5 cm，占最大允许值的43.3%，而氧的范围为4.0 cm，仅占16.0%。对初始液位倾斜与慢旋激励，流体类型对晃动演化的影响可忽略。

（4）微重力下，液体晃动幅度较大、慢旋速度较高均有可能造成贮箱底部暴露于气枕，因此必须有效控制。应根据贮箱含气率、分离完成要求等指标设计相应角速度。