人工神经网络理论及其在机器人运动与动力控制中的应用*

孙 涛

(安徽粮食工程职业学院 安徽合肥 230011)

生物的神经功能一般包括学习和记忆，学习是神经元间建立与修改连接的过程，记忆则是经过了一定学习或训练后的信息存储在神经元间的连接中。神经网络始于19世纪后期，人工神经网络的第一个应用为感知机及其学习算法。20世纪70年代，Teuvo Kohonen和James Anderson发明了具有记忆功能的新型神经网络，对神经网络的发展起到了极大的推动作用。20世纪80年代，反向传播算法公开发表，该算法可用于多层感知机的学习与训练中。神经网络已广泛应用于众多领域，人们对神经网络的研究依然在不断进行。王田苗[6]等分析了国内外工业机器人发展现状，对机器人在灵巧操作、自主导航、环境感知、人机交互与安全性等前沿技术的研究做了综述，提出我国工业机器人产业发展的若干思考和建议。叶壮[7]等为了解决单通道图像信号输入不能全面表达故障特征的问题，提出基于multi-channel one-dimensional convolutional neural network(MC-1DCNN)的故障特征学习方法，并对某型号齿轮箱故障诊断进行了方法验证。可见，神经网络的理论研究及其应用广泛而深入。机器人运动及其动力控制系统十分复杂且存在多种的非线性，因此采用人工神经网络对机器人进行控制是解决其动力控制问题的较为有效方法，并随着研究的深入而不断发展。

1人工神经网络基本理论

1.1人工神经网络的生物学原理

人脑含有大量的高度连接的神经元细胞，其基本结构包括胞体、树突、轴突和突触，树突用于接受电信号并将信号传给胞体，胞体对所接收的信号进行叠加后用阈值控制电信号由轴突输出。轴突是一条长的神经纤维，用于将信息传递给其他神经元，神经元的轴突和胞体、树突的连接点为突触，神经结构的改变主要表现在加强或减弱突触的连接，众多的神经元连接则构成了大规模的并行计算系统。

1.2 Hebb学习规则

Hebb学习的思想是由Donald O.Heeb于1949年在他的专著《The Organization of Behavior》提出，其基本思想是：当神经细胞A的轴突足够接近到能够激发神经细胞B，且反复而持续地刺激细胞B，那么细胞A或B中的一个或两个细胞将会产生某种增长过程或代谢变化，从而增强细胞A对细胞B的刺激效果。对与一个单层单神网络组织系统，其第i个神经元的网络输出为：

(1)

式(1)中：ωij为第i个神经元的输入p的第j个输入权值；pj为输入p的第j个输入；bi为第i个神经元的偏置值。

根据Hebb学习的思想，可得到网络权值的更新公式为：

(2)

式中，pjq为输入向量p的第q个输入向量的第j个元素；g为关于输入向量的函数；α为学习率；f为关于输出向量的函数。

式(2)为无监督的Hebb学习规则，因为式中没有考虑期望输出的效应，为了将期望输出反馈到网络系统，可将无监督的Hebb学习规则变换为有监督的Hebb学习规则：

(3)

式(3)中，t为关于网络输出的期望输出。

Hebb学习规则常用于联想记忆模型中，进行数据的聚类、模式识别等功能中，但网络的层数一般为单层，对多层神经网络的计算往往比较吃力，需考虑使用基于最小均方误差理论及进行网络方向传播机制。

1.3最小均方误差LMS算法与反向传播

考虑网络的期望输出为t，网络的输入向量为z，权值向量为x，则可得均方误差表达式为：

E[e2]=E[(t-xTz)2]

(4)

式(4)分别对网络的权值和偏执值进行求偏导，可得：

(5)

从而得到基于LMS算法的网络权值与偏执值的更新公式为：

(6)

基于最小均方误差LMS算法，设网络第m层的第i个神经元的敏感度为：

(7)

第m层的输出关于其净输出的导数为：

(8)

根据链式求导法则，可得敏感度的递归关系为：

(9)

网络权值和偏置值的更新公式为：

(10)

最小均方误差LMS算法和反向传播机制为神经网络的发展起到的极大的推动作用，随着理论研究的深入，发现径向基函数具有无限的函数逼近功能，因此可应用于许多非线性的控制系统中。

1.4径向基网路与机器人控制系统

径向基网络可用来解决多维空间的精确差值问题，具有无限的逼近特性，使用径向基网路逼近一个函数f(x)的算法为：

(11)

式(11)中x为网络的输入；j为网络隐含层的第j个节点；h为高斯计函数输出；为网络的逼近误差。

其逼近函数为：

(12)

式(12)中，f和W分别为逼近函数值和逼近权值矩阵值。

对于一个人n关节的机械手来说，其动力学方程可表示为：

(13)

式(13)中，M为正定惯性矩阵；C为惯性矩阵；G为重力项；F为摩擦力；τd为未知干扰项；τ为控制输入；q为系统变量。

设期望变量值为qd，则定义跟踪误差为：

e=qd-q

(14)

采用径向基网路对机器人控制系统中的不确定项进行逼近，得到基于径向基网络的机器人控制系统的控制律为：

(15)

式(15)中，Kv为误差的增益矩阵；r为关于误差的函数；v为用于克服神经网络逼近误差的鲁棒项。

对机械手动力学方程的各项进行逼近，可得：

(16)

可知，根据径向基网络的无限逼近功能，可对机器人动力学系统的各种确定及不确定项进行逼近，如对方程中的干扰项进行逼近，从而得到逼近函数，通过反馈发送到控制端或输入端，通过差分的方式即可将干扰消除。

2基于径向基网络的二连杆机械手控制

2.1二连杆机械手的动力学方程

采用径向基网路对2R型的二连杆机械手进行控制，首先建立二连杆机械手的动力学方程，根据公式，二连杆机械手的各项表达式为：

(17)

为了便于仿真，取某型号二连杆机械手的p=[p1p2p3p4p5]=[2.9 0.76 0.87 3.04 0.87]；取bj=0.2；系统的初始状态为[0.09 0 -0.09 0]；控制参数Kv为diag{20，20}。在MATLAB&Simulink中搭建上述控制模型，进行系统仿真。

2.2二连杆机械手控制系统的Simulink仿真

采用MATLAB的Simulink环境搭建基于径向基网络的二连杆机械手仿真模型，如图1所示。图中INPUT为系统的输入；CONTEOL为基于径向基网络的控制模块；PLANT为二连杆机械手的动力学方程模块。设置系统仿真参数包括连续时间系统仿真、ode45计算方法、仿真时间设置为20s。

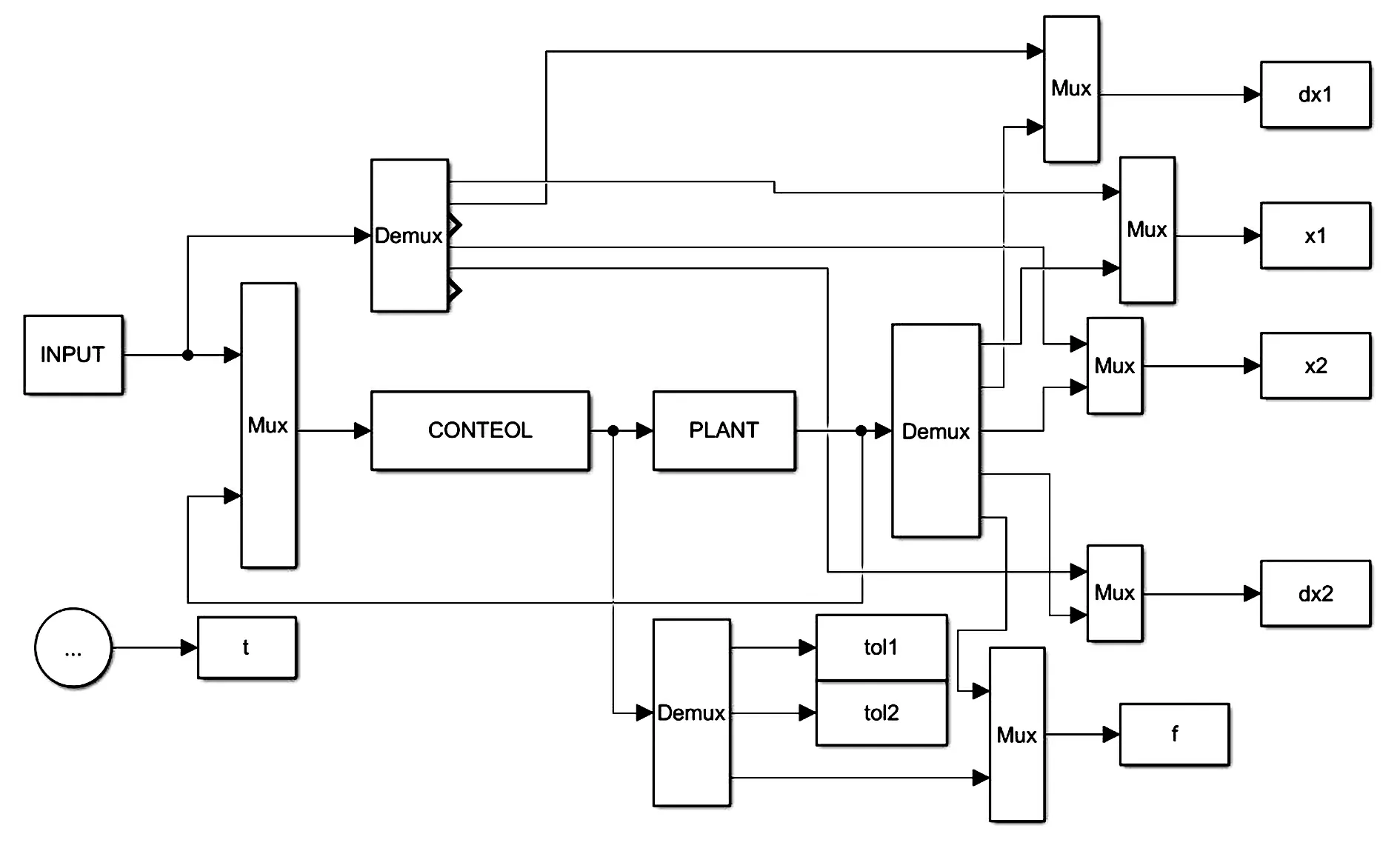
图1 基于径向基网络的二连杆机械手仿真模型

得到系统的连杆1和连杆2的位置跟踪情况、速度跟踪情况、控制输入情况和函数逼近情况，如图2-图5所示。根据图2的位置跟踪情况可知连杆1和连杆2随在起始时与期望位置不同，但随着时间的推移，其位置变化逐渐逼近于期望变化，在稳态阶段与期望输出几乎重合，达到了较高的控制精度。

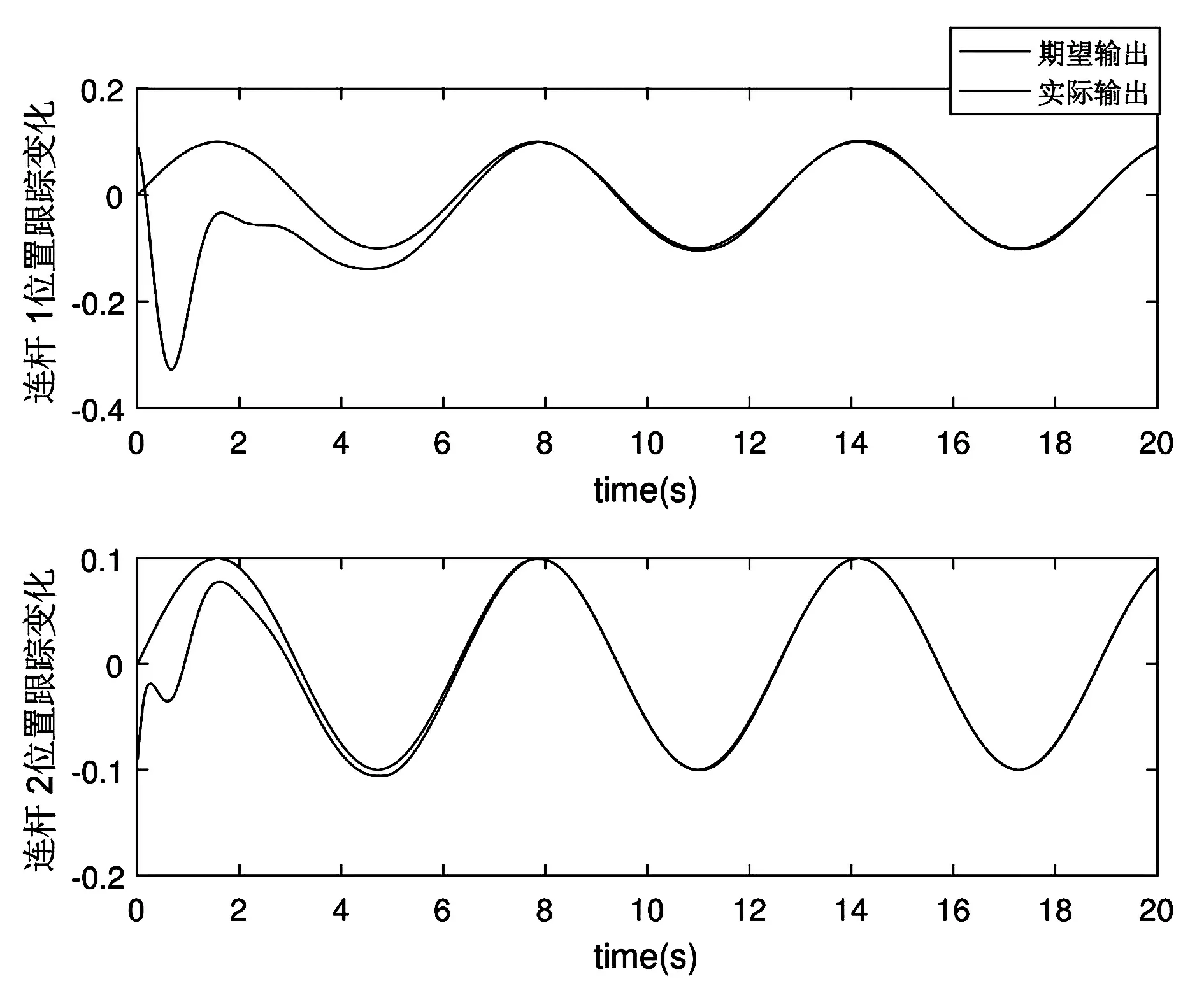
图2 连杆的位置跟踪情况

根据图3所示的速度跟踪情况可知，连杆1和连杆2的速度变化逐渐趋向于期望的速度变化，在初始一段时间内速度度有较明显的振动变化，但随着时间的推移，实际速度输出逐渐逼近于期望速度输出，并在稳态阶段时与期望速度输出几乎重合，这与连杆的位置跟踪情况是相对应的。

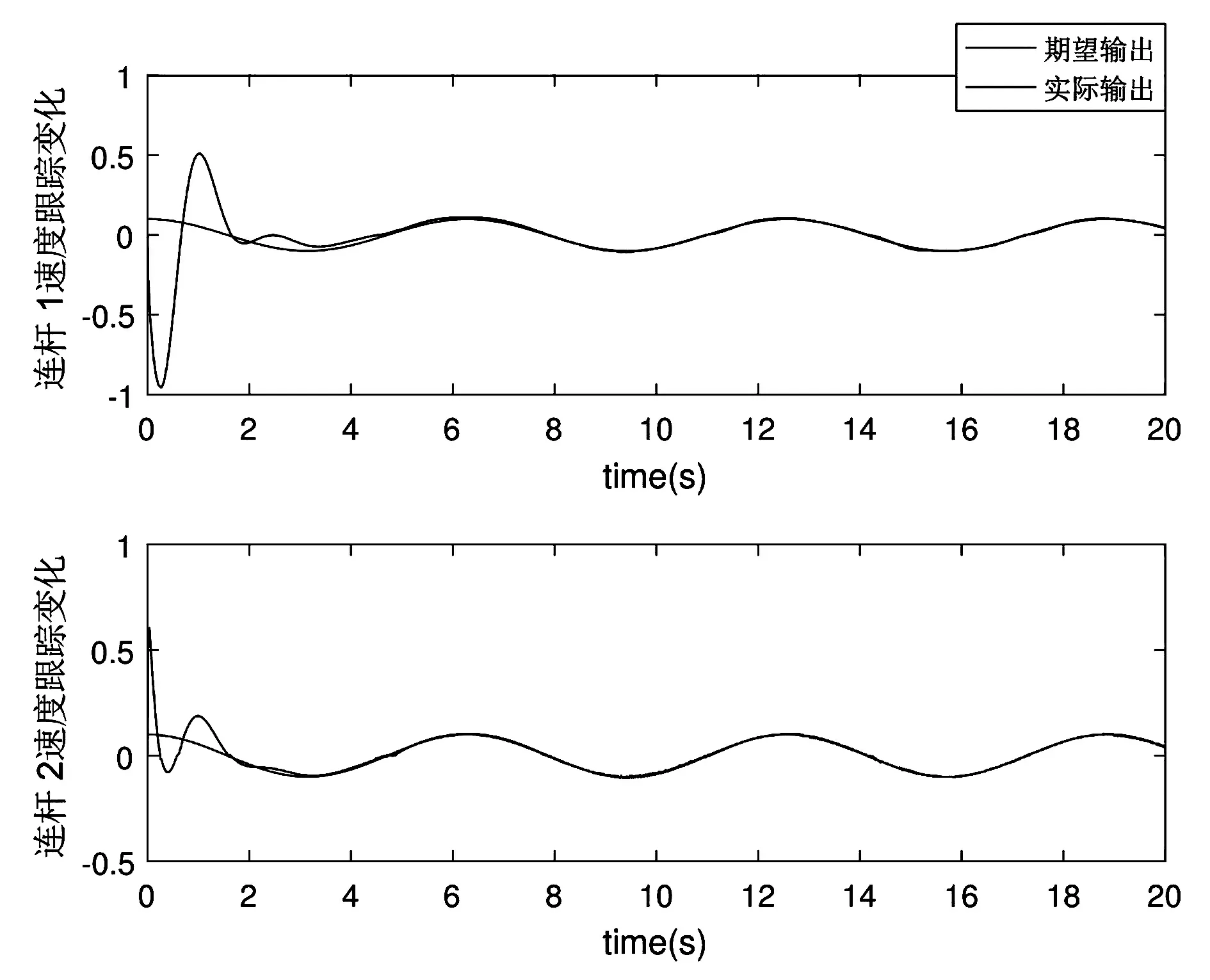
图3 连杆的速度跟踪情况

根据图4所示的连杆的控制输入变化情况可知，两连杆的控制输入在初始一段时间内有振荡变化，与连杆的位置和速度跟踪情况是相对应的，随着时间的推移，控制输入逐渐趋于稳定，连杆1的控制输入稳定在40左右，连杆2的控制输入逐渐稳定在8左右。可见控制输入稳态时表明控制系统已进入稳态阶段。

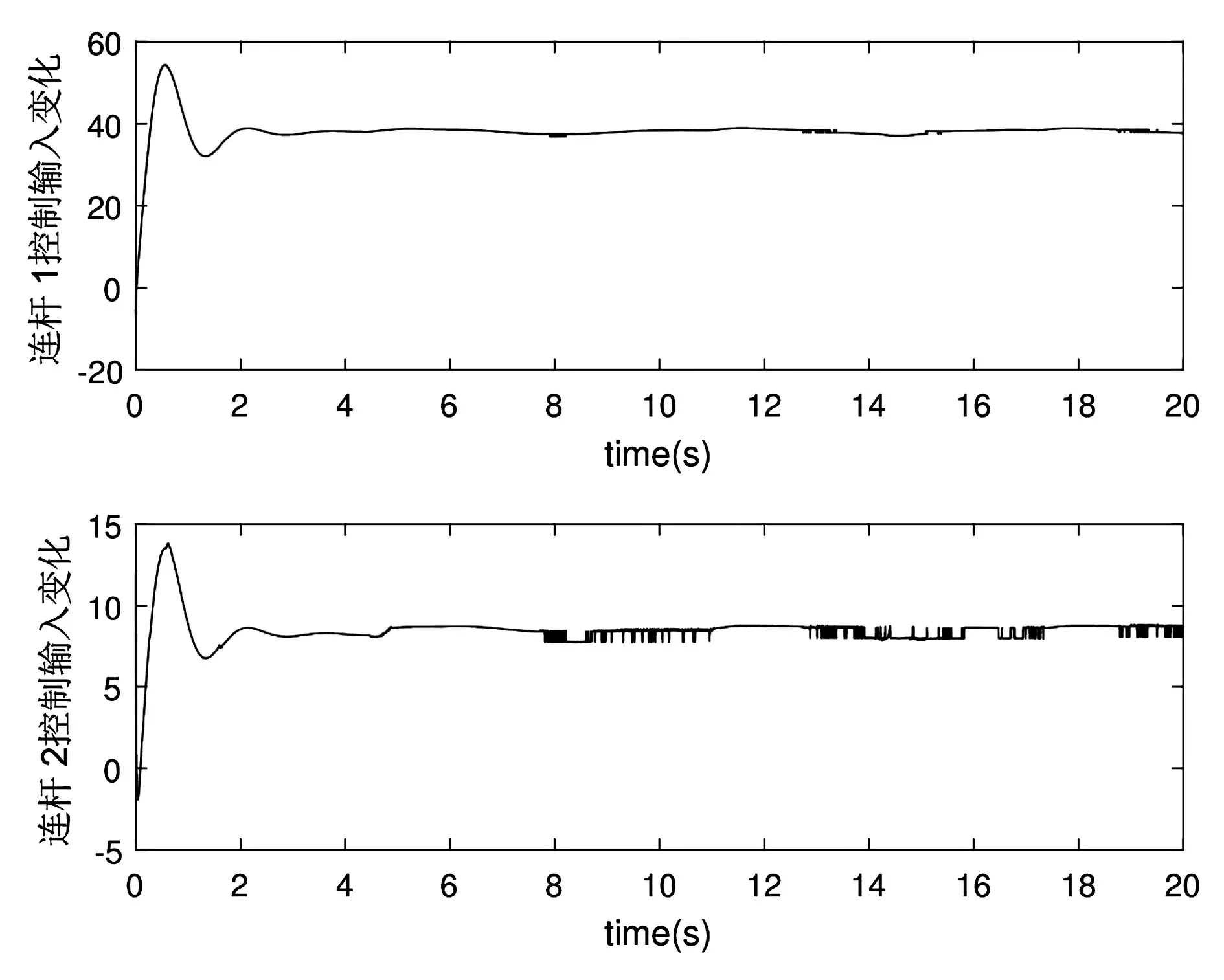
图4 连杆的控制输入变化情况

根据图5的函数逼近情况可知，在初始阶段实际逼近情况与期望逼近相差较大，在时间为6 s时，实际输出与期望输出进入稳态阶段。此时虽然仍有逼近误差，但误差已越来越小，表明基于径向基神经网络的逼近效果良好，达到了高精度控制的需求。

图5 函数逼近情况

3结论

研究表明，基于神经网络的控制系统达到了优良的控制效果，函数逼近效果良好，为基于神经网络的机器人运动与动力控制提供参考。文章对更高层次的神经网络模型未进行探讨，采用集成大规模的高层次神经网络的控制系统是高精度和高可靠性控制系统研究的一项重点内容。