虚力做功求解“猎犬追上狐狸的时间”

彭定辉

（江西省南丰县第一中学，江西 抚州 344500）

1 问题

“猎犬追上狐狸的时间”问题是一道经典的中学物理竞赛题，不仅可以用微元法或微积分方法求解，还可用MATLAB等专业软件进行数值模拟分析.［1-3］本文将另辟蹊径，用假想虚力做功的新方法来求解猎犬追上狐狸的时间.现将原题陈述如下：

例题.有一只狐狸以不变的速率v沿直线AB奔跑，猎犬以不变的速率u追击，其运动方向始终对准狐狸.如图1所示，某时刻狐狸在F处，猎犬在D处，FD⊥AB，且FD=L，设u＞v，问猎犬追上狐狸需多长时间？

图1

图1 题目图片

2 分析

为简化问题，选择狐狸为参考系，并借助矢量描述猎犬的运动情况.如图2所示，可知在运动过程中猎犬除了有始终指向狐狸的分速度u，还有相对狐狸由B指向A的分速度 ，即猎犬合运动的速度为u+.

图2 猎犬相对狐狸运动的两个分速度图

假设猎犬在运动中受到某个虚构的作用力——虚力δf，若此虚力做功的功率恒定，且又能知道其做功的大小，则无需计算猎犬的具体位置变化，可直接用公式W=Pt求时间.

3 求解

由于猎犬的速度为u+ ，故构造一个虚力

其中k为比例常量，则其做功功率为定值，即

如图3所示，该虚力由两个分虚力δf1=k u和δf2=-k组成.其中分虚力δf1与分速度u成正比，为一大小恒定的有心力，其方向始终沿矢径指向F点，力场如图4中实线所示.易知此力做功与路径无关，仅与径向位移有关.［4］因此在猎犬从D运动到F的全过程中，分虚力δf1做功为

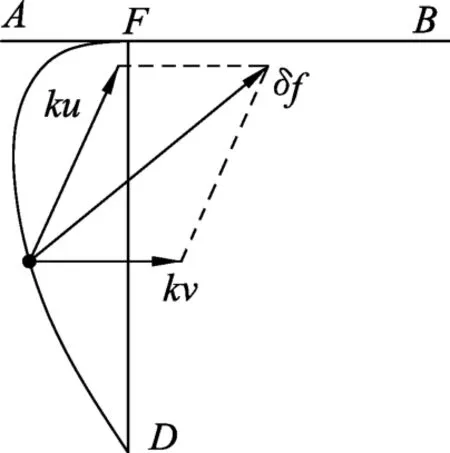
图3 猎犬所受虚力图

另一分虚力δf2与分速度 成正比，为水平向右的恒力，力场如图4中虚线所示.由于猎犬运动的总位移DF与该分力垂直，故分虚力δf2做功为0，即

图4 两个分虚力力场的分布图

因此虚力δf做的总功为

猎犬追上狐狸的时间为

这个解与其他方法计算的结果是一致的.

结束语：与微元法、微积分方法等相比，这种假想虚力做功的方法直接避开了对猎犬运动的细节处理，计算过程十分简洁.它作为“猎犬追上狐狸时间”问题的一种补充解法，对此类物理问题的视角选择和模型构建有一定的参考价值.