博弈论视域下高校体育竞赛的共赢分析
曾庆为 李彦龙
(湖北大学体育学院,湖北 武汉 430062)
在教育强国的新时代语境下,全国高校的教学改革不断推进,全面发展观深入人心,高校亦逐步从注重学生学习成绩的提高聚焦到学生综合素质的发展上,高校体育竞赛作为促进学生全面发展的重要手段备受关注。然而,在高校体育竞赛中,各种冲突层出不穷,如辱骂、斗殴,甚至发生群殴事件,这些不良事件对体育竞赛的良性发展和和谐社会的构建造成了严重影响。为此,本文通过分析发生冲突的原因,提出应对策略,为促进高校体育竞赛的健康可持续发展提供参考。
1 博弈论概述
1.1 博弈论的基本思想
博弈论又称“对策论”,属于应用数学的学科范畴,因此可以认为博弈论是研究社会现象的数学理论,但博弈不等同于竞争,它是用于研究竞争与合作的理论。“博”“弈”二字本代表两种棋类游戏,分别为六博棋和围棋,现今已知最早将“博”“弈”二字连用的人是孔子,他在《论语·阳货》中说的博弈是指用心地玩棋类游戏。
从游戏的角度来分析博弈论,不难发现博弈论的基本要素有主体(局中人)、策略、胜负(得失),需要有两个或多个局中人加入固定规则的空间内,通过单个或多个策略获得收益,完成博弈得到结果。因此,可认为博弈论是两人(双方)或多人(多方)决策的理论,其中任意主体的策略都会影响其他主体的收益,而任意一方也会在使用策略的过程中考虑他方的策略。
1.2 博弈论和高校体育竞赛活动的关系
首先,博弈论是分析多主体参与竞争的一种有效工具,从整体出发探讨各主体间的相互作用,突破了单一主体视野下孤立分析的局限性。体育竞赛活动的开展离不开竞争,高校体育竞赛活动也不例外。其次,从博弈论的角度看待高校、活动主办方和活动参与者之间的相互作用,能够更加明确地展现不同决策主体的个体利益最大化,以及整体利益最大化的产生方式。从个体最优与整体最优两种策略的差异和利益矛盾入手,探讨高校体育竞赛活动中存在的利益冲突,更易寻求使高校体育竞赛活动的开展趋于稳定的方法。
1.3 有关模型的假设
博弈决策的多主体均为完全理性,均为最大化自己的利益;完全理性是共同知识,每个参与人均对所处环境及其他参与者的行为形成正确信念与预期。
2 高校内体育竞赛活动开展的多重博弈
2.1 学校—活动主办方
2.1.1 学校—活动主办方博弈模型的建立
从多次体育竞赛活动的实践得出,学校和活动的组织者双方在决定己方策略的过程是相互依赖、相互影响的,因此可认为双方间存在动态博弈。由于双方都无法预测对方选择怎样的策略,现用字母p表示学校选择支持的可能性,用1-p表示中立的可能性;用字母q表示活动主办方选择开展的可能性,用1-q表示不开展的可能性。根据动态博弈理论可以得出学校—活动主办方博弈树(见图1)
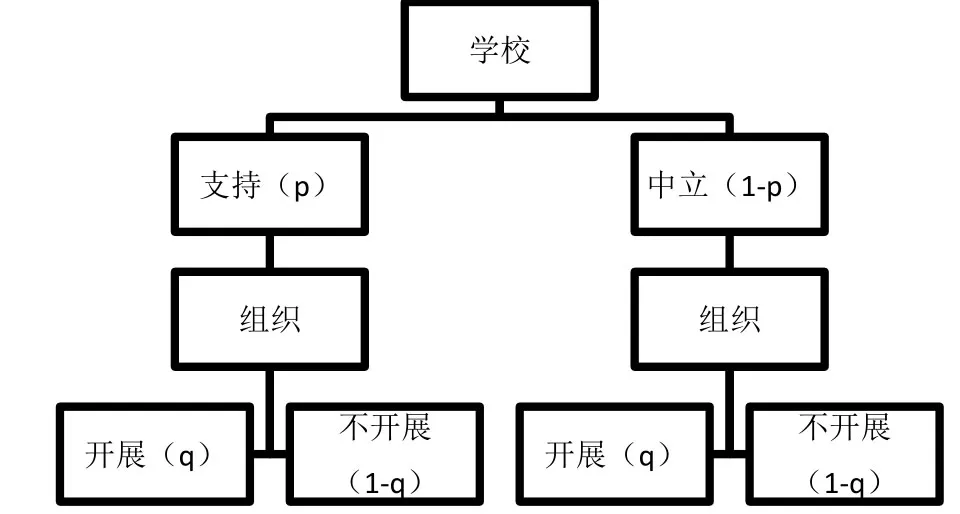
图1 学校—活动主办方博弈树
假设:学校支持需支付成本为C1,则中立成本为0;组织开展活动需投入成本为C2,则不开展成本为-C1;学校支持且组织开展活动的收益为U,同时存在额外收益E;学校中立且组织开展活动的收益仅为U,不存在额外收益。于是得到学校—活动主办方的博弈支付矩阵(见表1)。

表1 学校—活动主办方的博弈支付矩阵
从以上模型可知,学校支持且活动主办方开展活动策略构成此博弈的子博弈精炼纳什均衡,此时博弈双方的收益最大,分别为U+E-C2、U+E-C1。
通过学校—活动主办方的博弈支付矩阵可知:
学校支持的预期收益为:q(U+E-C1)+(1-q)(-C1)=q(U+E)-C1
学校中立的预期收益为:qU+(1-q)×0=qU
组织开展的预期收益为:p(U+E-C2)+(1-p)(U-C2)=pE+U-C2
组织不开展的预期收益为:0
因此,当学校支持的预期收益大于学校中立的预期收益,组织开展的预期收益大于组织不开展的预期收益时,即qE>C1,pE+U>C2时,博弈双方才会选择学校支持且活动主办方开展的策略。
2.1.2 学校—活动主办方博弈模型分析
通过学校—活动主办方博弈模型,从单次活动举办的角度来看,此博弈为有限博弈,但是学校和活动主办方双方的博弈是长期存在的,是一种利益均衡化的过程,单纯考虑某一阶段收益不能满足博弈双方的发展需求。将该博弈带入高校背景,不难发现活动主办方在博弈中一直处于劣势,因为学校存在多重选择,而活动主办方为了自身发展,更多时候只能选择举办活动。因此,活动主办方应该从长远出发,无论现阶段学校是否支持都应该积极参与、主动争取,从而获得学校的重视,赢得学校的支持。同时,博弈主体存在个体差异,抛开“博弈决策的主体是理性的”的假设,决策主体的个人偏好也应成为决策双方决定策略的影响因素。
2.2 活动主办方—活动参与者
2.2.1 活动主办方—活动参与者博弈模型的建立
竞赛活动能否顺利举办,通常情况下受到两方面影响,一方面活动主办方决定是否举办该竞赛活动;另一方面,竞赛活动需根据活动参与者的报名情况最终确定是否举行。在这一过程中,活动主办方和活动参与者二者所采取的策略相互影响、相互依存。根据动态博弈理论可得出活动主办方——活动参与者博弈树(见图2)。

图2 活动主办方——活动参与者博弈树
假设:第一主办方举办需花费成本为C1,获得效益为U1;第二参与者参与活动所需成本为C2(包括时间、精力等),获得收益为U2(包括荣誉、社交等)。
可得到主办方以及参与者参加博弈的效用函数为:
举办且参与:主办方U1(X1)=U1-C1;参与者U2(Y1)=U2-C2
举办且不参与:主办方U1(X2)=-C1;参与者U2(Y2)=0
不举办:主办方以及参与者U1(X3)=U2(Y3)=0
从以上模型可知,主办方举办且参与方参与策略构成此博弈的子博弈精炼纳什均衡,此时博弈双方的收益最大,分别为U1-C1、U2-C2。
2.2.2 活动主办方—活动参与者博弈模型分析
活动主办方—参与者的博弈存在很明显的“先动”特点,博弈开始时行动存在先后顺序,即主办方先决定活动是否举办。先动者的策略会对后动者的策略选择产生影响,而后动者则可以通过观察先动者的策略决定己方策略,这时就存在先动优势、先动劣势两种可能。
在活动主办方—参与者的博弈中,主办方也并非完全随机地对举办和不举办进行选择,因为在活动的前期策划阶段主办方可通过调查等形式广泛征集意见。由于此博弈双方都能获得不少于开始时的收益,因此将其看作双赢对局进行分析。在博弈具备帕累托改进性质的基础上,博弈开始前调查结果的信度较高就可用作策略参考,博弈先行方在很大程度上能够通过完备的前期准备来减少先动劣势(举办且不参与)的可能性,进而减少损失。同时,观察博弈参与者(后动方)的效用函数可知,其不受损的概率较大,唯一利益受损的条件为“U2-C2<0”。从多次体育竞赛活动的实践中可知,造成“U2-C2<0”的原因主要源自活动主办方(先动方),如竞赛赛程安排不合理、竞赛分组不科学、临场人员工作存在问题等。而这些对竞赛活动造成的影响可以通过前期完备的准备工作去减少。
从实际情况出发,该博弈的主体双方并不了解对方准确的策略空间以及支付函数,因此在此博弈的过程中,博弈双方的信息需及时交换,如通过问卷调查进行意向分析,达成帕累托优化。
2.3 体育竞赛活动—其他同类竞赛活动
2.3.1 体育竞赛活动—其他同类竞赛活动博弈模型的建立
假设存在一个体育竞赛活动和另一个其他同类竞赛活动,且两者的面向人群基本一致,由于高校内学生活动时间有限,两者在赛程安排上基本一致,致使有意向参赛人群仅能报名一项竞赛活动。这时博弈双方都存在更改时间、计划不变两种策略。
假设:双方更改时间造成的损失为E,双方保持计划不变获得的净利润为U;当一方更改时间而另一方保持计划不变时,计划不变的一方能够获得的额外收益为Δe(更改时间方的部分前期投入),则另一方会损失Δe;双方时间冲突,造成的双方利益受损均为P,且P>E,P<E+Δe。于是得到体育竞赛活动—其他同类竞赛活动博弈支付矩阵(见表2)。

表2 体育竞赛活动—其他同类竞赛活动博弈支付矩阵
从以上模型可知,博弈双方最好的策略是双方均更改时间,但由于博弈双方并不知道对方的选择,则存在以下推理:若对方选择计划不变,己方选择更改时间或计划不变,对方收益均不低于己方:U+Δe>U-P>U-E-Δe,因此在这一假设中,己方选择计划不变所获收益更大;若对方选择更改时间,己方选择更改时间或计划不变,则己方收益均不低于对方:U+Δe>U-P>U-E-Δe,因此在这一假设中,己方选择计划不变所获收益依然更大。综上所述,无论对方选择哪一种策略,己方都会选择计划不变,同理对方亦会得出相同结论。所以,此博弈最终结果是非帕累托最优的纳什均衡,这就是典型的“囚徒困境”问题。
2.3.2 体育竞赛活动—其他同类竞赛活动博弈模型分析
在同类型竞赛活动的竞争关系中,博弈是不可避免的。“囚徒困境”问题中,博弈双方通过个体最优策略无法达成整体最优策略组,这时就需要外界介入辅助沟通或制定策略。但从竞赛活动的长期发展来看,阶段性的“囚徒困境”问题并不可怕,活动质量才是竞赛活动长远发展的核心竞争力,是决定活动能否长期开展的重要依据。而活动参与人数、参与体验则是活动质量评价的两个重要指标。从另一角度来看,活动参与人数越多,参与体验就越难达到一个高的水平,这就需要活动主办方从自身实力考量,决定活动预期规模。由于高校的学生活动经费有限,提高活动质量在下一阶段的经费申请、活动等级审批等方面都存在明显优势,从而产生良性循环,这是这场博弈中所获的额外收益。
3 探索高校体育竞赛活动开展博弈中的多主体共赢策略
3.1 能力适合是实现共赢的前提
能力一词在这里笔者将它解释为影响力,联系的普遍性告诉我们,一个人的能力能够对周围的一切人和事物带来这样或那样的影响。在博弈中,他人试图与你合作是因为你的能力会对他的策略产生不可忽视的影响,而这一影响又可分为两个方面:第一,你的能力能够使他人变好,对他人存在利用价值,这时他人就会努力去讨好你,从而得到利益交换,甚至有直接获取利益的可能性。第二,你的能力能够使他人变差,对他人构成威胁。在这种情况下,当他人自身的策略函数无法消除你对他的威胁时,便会选择与你合作,试图避免伤害。
因此,能力是合作的前提,当自身能力对他人没有影响或者影响较小时,他人就会选择无视你,合作更是无从谈起。体育竞赛活动组织应该面对自身,从提高活动质量出发,正确看待其竞争优势。一方面,充分发挥活动本身灵活性、多样性的特点,创新活动形式,提高竞赛活动的趣味性和娱乐性;另一方面,多关注国内外相关资讯,了解行业发展趋势及走向,提高竞赛活动的专业性,从而吸引不同需求参赛者加入该体育竞赛活动中。
3.2 合理竞争是实现共赢的保障
高校体育竞赛活动开展的博弈是无法避免的,上述模型中都或多或少存在利益冲突,但也并非是“零和博弈”和“常和博弈”。我们必须明白构建单次博弈模型是分析多次博弈的基础,分析多次、无限次博弈是构建单次博弈模型的目的。由于体育竞赛活动开展的博弈长期存在,我们必须放弃看似理性的“逆向归纳法”(如蜈蚣博弈),从正向出发,思考如何利益最大化。恶性竞争中博弈主体常常通过非常手段试图取得垄断地位,但这一行为并不利于主体本身甚至行业的长期发展,因为它是以驱逐竞争对手为目标的一种竞争方式。而合理竞争则是一种承认对手、承认差别的竞争,竞争各方在博弈过程中相互学习从而构成合作。在高校体育竞赛活动开展的博弈里,竞争各方都应是相互依存的关系,不同活动主办方都对校园文化的发展有所贡献,任何活动在高校内的消失对于校方和其他活动主办方来说都会造成损失,而活动主办方为活动参与者提供平台,参与者为主办方提供反馈,二者缺一不可。
体育活动主办方与其他各方是一种相互有利的关系,利用奖品、学分等附加因素获利是合作中的竞争,但举办大规模、多项目积分赛便是竞争中的合作。从这个角度出发,合理竞争就是一种合作性的关系,寻求合作是高校体育竞赛活动长期开展的必然之路。面对外界体育竞赛活动组织应努力寻求多方合作,实现优势互补,拓宽资金渠道,使资金来源多样化,同时主动学习高校内相关政策,合理利用规则,努力把握政策福利,增强活动稳定性,为体育竞赛活动长期发展做好铺垫。
3.3 构建利益共同体
人是理性的,但人的理性选择是基于已知条件,在博弈中由博弈的公共知识产生。在可以达成博弈更优解帕累托最优的情况下,选择个人最优解,其实双方在一定程度上都损失了部分收益。为了使个人、集体利益最大化,我们必须明白一个概念——“未来理性”。博弈所带来的任何后果都是会在未来发生的,仅仅基于现有公共知识的理性不是“未来理性”,我们需要以最优解为基础,努力形成新的公共知识,这才是“未来理性”背景下我们应该做的事情。为了构建更多的公共知识体系,博弈主体需要进行相互间的沟通,体育竞赛活动组织需要与校方沟通,表明己方开展活动的意愿,积极了解校方的选择条件以及支持力度,利用活动策划等方式构成“体育竞赛活动组织—学校”间的新的公共知识。体育竞赛活动组织还需利用校方与其他活动组织方之间的联系,促使校方在时间、场地等方面做出统计与协调,从而减少博弈双方(多方)的冲突,尽可能提高资源利用率,提高投入回报比率,并且要制定完备的活动评价机制,对各活动进行评定,遵循办事原则,将体制、机制落到实处。通过校方与参与者之间的必然联系,体育竞赛活动组织、其他活动组织与参与者之间的偶然联系,加深各活动组织的影响力,共建校园文化,最终构成利益联盟,将“我”变成“我们”。
然而,利益联盟是一个不稳定的共同体,因为利益因素集聚,当利益联盟不能给联盟中的个体带来好处时,个体往往会选择违背约定,因此在博弈里的联盟必须建立反反悔机制。在上述联盟中体育活动组织方应当积极地给校方反馈合作效果,同时建立自己的考核机制,有选择性地选择合作方。
3.4 各取所需实现共赢
没有明确归属的任何资源都可能成为争夺的对象,在高校体育竞赛活动开展的博弈中,我们可以采取两种分配方式的混合方式,以期达成各得其所的目的。首先是收益与期望贡献成正比的分配方式,由于任何分配都需要提前制定分配规则才能尽可能地减少冲突,采用夏普利值衡量分配标准是一种可行的方式。夏普利值是指在各种可能存在的联盟次序下,成员对联盟的边际贡献之和除以次序和。这种分配方式适用于需求近似相同的联盟成员,可以用于体育竞赛活动组织以及其他活动组织的利益分配。还有一种适用度更广的分配方式,即纽约大学教授伯拉姆兹提出的一种双赢的分配方式,将资源客观地划分为等价的n个部分(n=参与分配成员数量的倍数),由成员独立为每个部分估值,最终按成员对各部分的需求度决定分配结果,这样的分配方式更适用于需求不同的联盟成员,使之各取所需,实现共赢。

