2.5D有限元建模关键问题
王瑞 胡志平 任翔 李芳涛 温馨
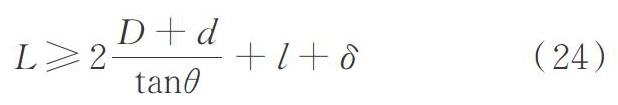
摘要: 为了提高2.5D有限元数值计算的求解精度及建模效率,分析了移动荷载作用下地基系统的动力响应特点,确定了计算域选取及网格划分的基本规则,评价了地基分层对波场的影响及边界的波动吸收效果,提出了可以规避边界影响的建模思路。分析结果表明:当计算域尺寸满足低频振动要求(约60 m)时,反射波对计算结果的影响可以忽略;建模时可以采用辐射状网格划分,最小网格尺寸需满足高频振动要求(约0.5?1.0 m)。荷载运行速度小于地基瑞利波速时没有波动传播现象,建议直接采用固定边界;荷载运行速度大于地基瑞利波速时可以通过切取局部计算域的方式规避反射波的影响,此时计算域半宽和纵向空间范围的选取需要遵循与马赫锥锥角和列车全长相关的几何关系。荷载影响深度内的地基分层会扰乱地基波场,当地基上覆软弱土层或软弱夹层时,波动会在软土层聚集并在加载点后形成多个马赫锥。
关键词: 分层地基; 建模; 2.5D有限元; 网格划分; 吸收邊界
中图分类号: TU472; TU311.3 文献标志码: A 文章编号: 1004-4523(2021)01-0080-09
DOI:10.16385/j.cnki.issn.1004-4523.2021.01.009
引 言
随着铁路交通运量及速度的不断提高,列车运行引发的环境振动问题逐步凸显。针对列车荷载作用下路基内部动应力的分布规律对路基长期沉降及稳定性影响规律的研究也日益增多。现有研究方法主要有现场实测、室内模型试验及数值模拟三种,其中数值模拟方法被广泛采用,计算结果的精度及可靠性也在逐步提高[1?7]。为了兼顾计算效率,以往常采用二维平面问题研究列车荷载作用下地基系统的动力响应规律[8]。在地震工程领域,研究P波和SV波入射引发的场地动力响应规律时可以基于场地特点将三维问题简化为平面应变问题[9]。研究列车荷载引发的地基动力响应时,虽然地基断面大多沿荷载移动方向保持不变,但在移动荷载作用下地基系统的响应特点并不符合二维平面问题的相关假定。Yang等[10]分析了移动荷载作用下二维和三维地基的动力响应规律,指出当三维问题中荷载移动速度无限大时地基的动力响应规律与二维问题一致。也就是说,简化的二维平面模型不足以揭示列车移动荷载下地基系统的动力响应规律。
2.5D有限元方法是计算移动荷载作用下地基系统三维动力响应规律的高效方法之一,其基本原理是假设路基断面沿列车运行方向保持不变,通过在列车运行方向上的波数变换避免了该方向上的有限元离散,大大缩减了模型的自由度[7]。影响有限元计算精度的因素主要体现在网格划分、边界条件选取、地基材料参数及收敛判据等方面。由于地表作用移动荷载情况下地基的响应问题属于典型的內源问题(即波源在计算域里面),其波动激发特点及传播规律具有很强的特异性[5?7]。地震工程问题数值建模过程中采用的网格划分、计算域选取及吸收边界条件设置等规则无法直接引入。
关于2.5D有限元建模过程中的边界处理及网格划分问题,周彪等[11]以瑞利波速为基准探讨了不同边界条件下的计算域选取和网格尺寸对计算结果的影响,指出计算域半宽以大于1.5倍瑞利波速为宜。然而,笔者分析路基系统动力响应问题时发现上述规律尚不足以揭示2.5D数值模型特点和网格尺寸确定、计算域选取及吸收边界设置时的基本规则。采用有限元方法研究交通荷载作用下地基动力响应问题时大多学者并未对网格划分、计算域选取及人工边界的设置情况进行深入探讨。有鉴于此,本文从內源移动荷载作用下地基系统的动力响应特点及相关科学问题入手,论述了网格及计算域尺寸选取基本原则,评价了地基分层对波场的影响及人工边界的波动吸收效果,给出了可以规避边界影响的建模建议。
1 算法验证
本文以MATLAB软件平台编制2.5D有限元程序,有限元的网格划分和单元、节点位置等信息通过ANSYS有限元软件实现并导出,理论基础及建模过程详见文献[7,10?11]。
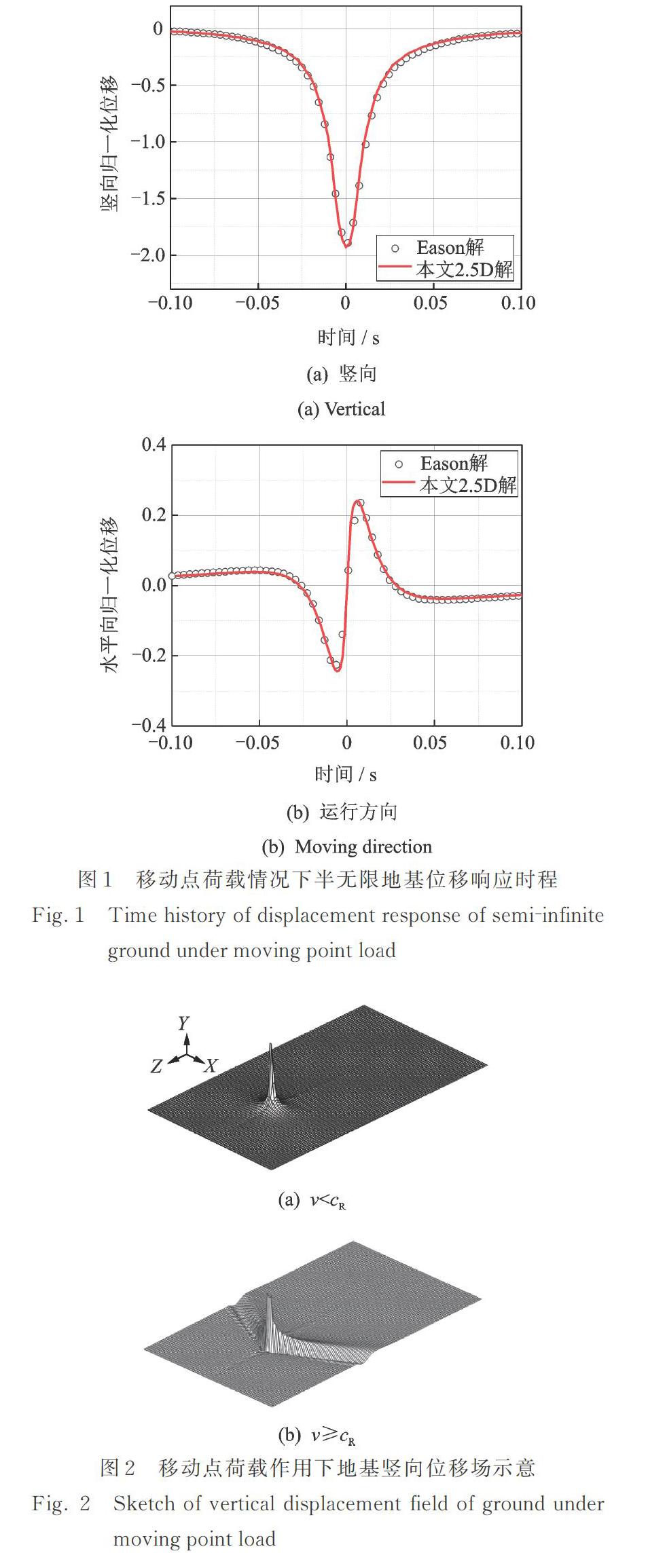
为了验证计算程序的可靠性,计算了均匀半空间表面作用移动点荷载时的地基动力响应规律,采用Eason经典解为对照组。计算域深度及底部边界情况按要求设置,模型半宽统一设置为30 m,网格采用四节点等参单元划分,尺寸介于0.4?1.0 m之间。侧边界暂统一设置为固定边界。移动点荷载采用狄拉克函数模拟,移动速度70 m/s,地基参数参照文献[7]。选择加载点下深度1 m处观察点的位移响应进行验证,将响应数值乘以2πρcs2/P进行归一化,其中P为荷载大小,cs为剪切波波速,ρ为介质密度。观察点竖向及沿荷载运行方向的归一化位移响应如图1所示。对比可以看出本文提出的2.5D有限元程序可以用来计算移动荷载作用下的地基响应问题。
2 內源移动荷载下地基响应的特点
2.1 运行速度的影响
以半无限地基表面作用一点荷载为例,当荷载移动速度为0时为静力问题,地基变形可以通过弹性力学计算得到;当荷载移动速度无限大时,三维地基响应符合平面问题基本规律,即此时可以等效为沿运动方向的线荷载[10]。当荷载移动速度介于两者之间时,地基响应随荷载移动速度的提高呈现两种不同的特点。当运行速度低于地基瑞利波速时(v<cR),荷载的移动会引发土体主应力轴的旋转,但无波动传播现象,如图2(a)所示;当运行速度不低于地基瑞利波速时(v≥cR),马赫效应出现,土体主应力轴旋转的同时有波动向外传播,此时环境振动的影响范围显著增大,如图2(b)所示(图2由本文2.5D有限元程序计算得到)。上述移动荷载引发地基响应的特点是决定数值建模过程中网格划分、计算域确定及边界条件选取的重要依据。
2.2 边界条件
为了模拟无限域对外行波的吸收效果,研究人员基于工程波动及有限元相关理论提出了多种行之有效的人工边界条件。由于研究內源移动荷载问题时无需像地震工程问题一样在满足波动吸收效果的同时实现边界处的荷载施加[12],吸收边界的选择较为自由。研究人员往往根据自身研究背景选取不同的人工边界条件,目前常见的有黏弹性边界、无限元边界、多层黏性边界、薄层单元及固定边界等[5,10,13?15]。
2.3 研究范围选取
移动荷载作用于地基时,无论研究地基内部的动应力分布規律还是地基表面的环境振动规律,其影响范围都是重要指标之一。已有研究表明,地基内部动应力的衰减深度一般不超过20 m,地基表面环境振动的衰减距离一般不超过40 m。研究环境振动时,地表振动强度衰减规律十分重要,一味选择较小的计算域(以至于地表波动在域内无法充分衰减)在一定程度上与研究目标相悖。在慎重选择人工边界条件的情况下,适当扩大研究区范围很有必要,分析时切取的有限域应该适当包络移动荷载的影响范围。此外,由于边界上的动应力较小而不致产生明显的波动反射,部分研究者建议直接采用固定边界研究列车荷载在地基内部的传播规律[5]。
3 计算域选取及网格划分原则
为满足波动数值模拟的精度要求,在有意义的最短波长内需要包含足够数目的空间步距才能避免由于对连续介质的有限元离散引起的“低通效应”对结果的影响[15]。Yang等根据2.5D频域计算方法特点系统地总结了计算频率对网格划分和计算域尺寸的要求,指出不考虑荷载自振时特定计算频率ω时,对网格尺寸r及计算域半宽R的要求如下式所示[16]
式中λs和ks分别表示考虑荷载移动速度时S波在计算频率ω情况下的波长和波数。对于P波和表面R波(瑞利波),只需将其中剪切波波速cs改为相应波速即可。网格尺寸和计算域半宽为地基材料参数、车速和计算频率的函数,高频分量限制网格尺寸,低频分量则决定了计算域范围。为了兼顾软、硬两种地基材料,本文分别在cs为50和100 m/s情况下绘制了网格尺寸随车速及计算频率的变化规律(如图3所示),可以看出最大网格尺寸并非随加载频率和列车速度单调变化。考虑到有限元网格划分及计算域的选取需要同时兼顾计算效率及精度要求,结合实际列车荷载作用下地基响应的频谱特征[7],建议考虑高频分量时(15?30 Hz)最大网格尺寸在0.5?1.0 m,模型半宽大于1.5?3.0 m即可满足要求;低频时(0.5 Hz)最大网格尺寸要求可以适当放宽至约20 m,半宽大于60 m即满足要求。为了兼顾高低频分量,目前常用的方法是在建模时采用辐射状网格划分,以加载点为基准网格尺寸逐渐增大,最小网格尺寸满足高频要求,计算域尺寸满足低频要求。需要注意的是每次向外扩展网格时满足“当前计算域尺寸>3倍当前网格尺寸”即可。
4 移动点荷载下的地基波场及边界吸收效果
4.1 模型情况
4.1.1 网格划分及基本计算参数
切取计算域的半宽为75 m、深度为36 m,网格尺寸按0.5,1.0,2.0 m三级辐射划分,如图4所示。地基土体为单一土层,参数取密度ρ=1600 kg/m3,剪切波速cs=90 m/s,泊松比υ=0.3,阻尼系数β=0.04。荷载移动速度v=100 m/s,荷载大小为100 kN。
4.1.2 积分变换参数
由于2.5D有限元是在频率?波数域内完成系统动力方程的求解,之后通过傅里叶反变换获取时间?空间域的动力响应,时程响应满足Z=vt的变换规律。本文坐标轴方向如图2(a)所示。由于列车长度是恒定的,一般在特定的纵向(Z向)空间范围L内展开计算。根据采样定律,当车速为v、采样点为N时,计算时长T为
由于并未在Z向进行网格划分,时程曲线精度取决于积分变换的精度,当采用的频率分辨率包含较为全面的频谱信息时即可获得准确结果。积分变换的关键参数由L,N和v共同确定,需根据具体工况谨慎选取。建议可以通过空间步长?L来界定上述参数,其数值不宜超过0.5 m,否则可能会遗漏时程响应的关键信息。本文取L=150 m,N=600。
4.2 边界条件的影响
4.2.1 黏弹性人工边界
考虑到以往黏弹性边界参数推导过程中忽略了介质阻尼对波动传播的影响,理论上不甚完备。本文首先基于三维黏弹性本构参数下的波动传播理论推导柱面波传播时的黏弹性边界参数取值。关于2.5D数值分析中的复阻尼及波动在黏弹性介质中的传播情况介绍详见文献[7,17]。
关于2.5D有限元人工边界的波动吸收效果,以往多用观察点的时程曲线进行考量,鲜少通过波场直接观察列车荷载激发的应力波在边界处的反射情况。与时程曲线对比,波场快照可以更加直观且全面地展现波动在边界处的传播细节。黏弹性边界情况下地表面位移场如图5所示。从三维云图和波场快照可以看出,在采用黏弹性边界时边界依然有轻微波动反射出现,根本原因是其在理论上不能完全满足严格的波动吸收条件。
4.2.2 无限元边界
为了验证上述论述,结合本文等参数四节点单元构造如图6所示的四节点无限元单元[19?20]。
采用无限元边界时地表面竖向位移的波场快照如图7所示。可以看出此时边界处有轻微波动反射现象,其原因依然是衰减函数的形式及衰减因子等的取值只满足近似意义上的波动传播条件,并不完全严谨。因此在采用人工边界时追求完全意义上的波动吸收效果还不够现实。
4.3 地基分层对波场的影响
实际工程中上述单一地层情况较为少见,更多时候地基呈现明显分层特征,波动在地层分界面上的透反射会导致波场变得较为复杂。因此有必要揭示分层地基情况下地表移动荷载激发的波动传播规律。在图4所示网格划分基础上,分别设置上硬下软、上软下硬和软弱夹层三种分层地基讨论波动传播规律,地基分层及土层参数如图8所示。设荷载移动速度为100 m/s,采用黏弹性人工边界,其余加载参数与上文一致。
三种典型分层地基情况下场地竖向位移波场如图9所示。与图5对比可以看出,地基分层对场地波场影响显著,地表出现多个马赫锥,且马赫锥的位置与中断面上波场分布有明显的对应关系。在软、硬土层分界面上可以看到波动反射现象。对比图9(a)与(b),(c)可以看出,当地基上覆软弱土层或者软弱夹层时,波动会在软土层聚集并且在加载点后形成多个马赫锥,拉长波场范围。
另外,在图9(c)中马赫锥前方的三角区域可以观察到轻微的波场扰动。通过图10中并列的两张波场图片可以看出,经傅里叶反变换得到的场地响应表现出明显的周期性,该扰动是由傅里叶变换的周期延拓性质带来的虚假反射。
为了避免虚假反射的影响,在计算时需要保证纵向影响区域被全部包括在计算范围L内。基于上述认知,在扩大L至300 m情况下(N=1200),分别获取上覆软土层厚度分别为4.5,10.5和36 m情况下地基波场如图11所示。
此时由于选取的空间范围较大,虚假反射消失。另外,随着上覆软土层厚度的增加,分界面上波动的透反射对底边波场的影响逐渐减小,加载点后部的马赫锥渐趋于消失,马赫锥锥角也渐趋一致。当地层分界面在列车荷载影响深度以下时可以忽略地基分层对波场的扰动。由于实际工程地质条件各不相同,本文仅针对三种典型地基做了趋势性分析,以期为后续针对具体工程的定量研究提供参考。
4.4 吸收效果評价
以图5,9及11所示工况为例获取不同地基情况下波动幅值在横向(X向)上的衰减规律如图12所示。虽然从波场快照上可以看到波动反射现象且反射情况随着地层条件变化各不相同,但在模型边界处幅值衰减率均不超过2%。因此从工程角度分析场地动力响应规律时可以忽略反射波的影响。上述认识是在计算域半宽为75 m情况下获得的,模型半宽不同时波动的反射情况会有所变化。
5 建 议
研究移动列车荷载作用下地基响应规律时,虽然常用的人工边界不能满足严格的波动吸收条件,但是可以通过计算域的合理选取获得良好的计算效果。本节在上文分析基础上,结合荷载速度变化时地基响应的基本特点和网格尺寸及计算域选取的基本规则,探讨可以获取无反射波扰动波场响应的建模思路。
5.1 工况一,v<cR
当荷载移动速度小于地基材料瑞利波速时没有波动现象产生,且荷载影响范围有限,如图2(a)所示。此时吸收边界条件对结果没有影响,设置边界条件时需要注意的是不要选择不具备弹性恢复能力的人工边界(如黏性边界),建议可直接采用固定边界。
5.2 工况二,v≥cR
5.2.1 模型半宽
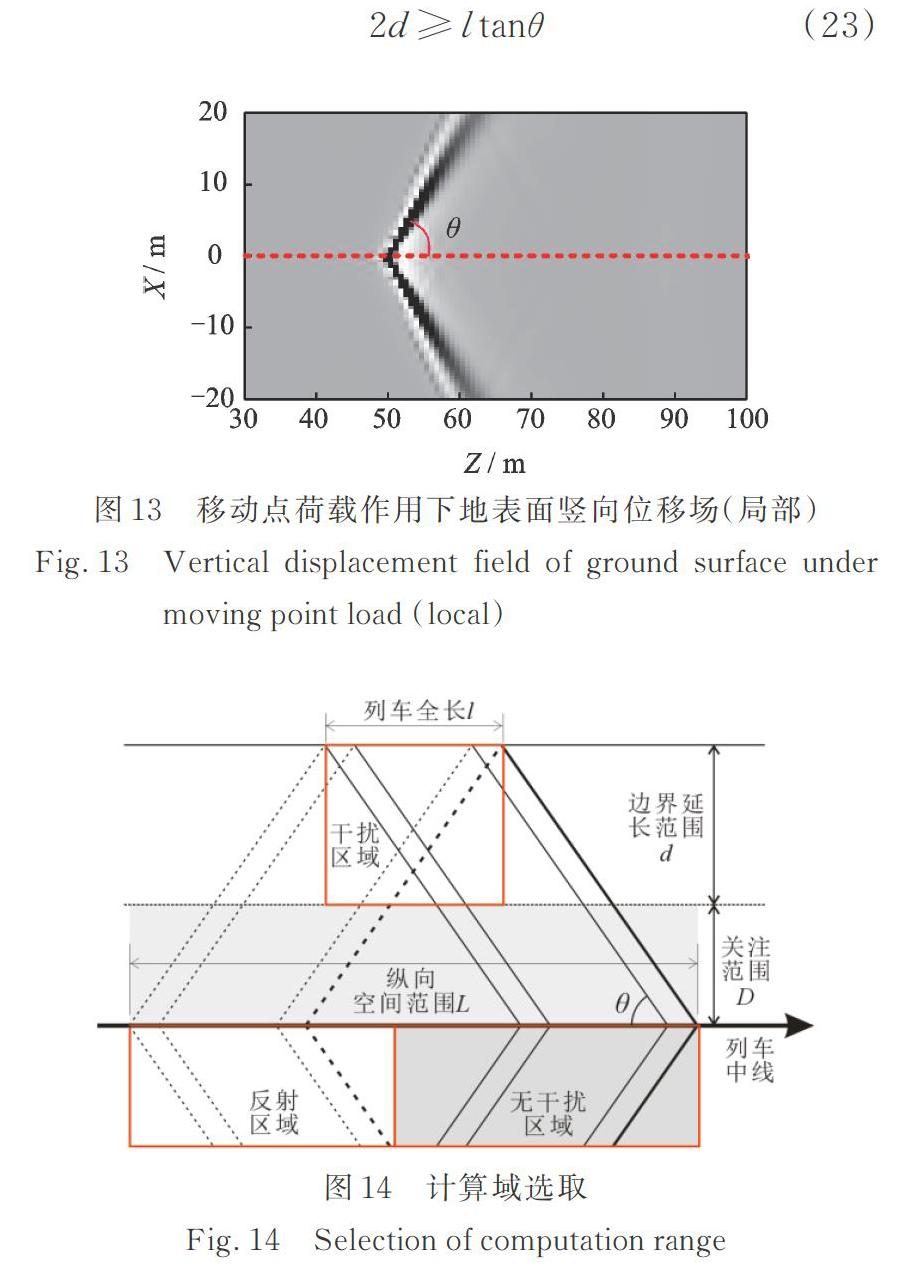
当荷载移动速度不小于地基材料瑞利波速时需要按照动力问题处理。若需要获得完美的计算效果,可以通过切取局部场地实现。图13为切取图5中局部场地响应得到的地表竖向位移场。波场较为完美的原因是移动点荷载激发的地表波动会以“马赫锥”的形式向远处传播,锥角θ与地基参数及列车速度之间的关系为:θ=arcsin(cR/v)。根据Snell定理,界面上发生波动反射时同一种波形的入射角和反射角是一致的,在入射波和反射波夹角范围内的场地响应不受影响。因此,在计算精度要求特别高时可以采用附加计算范围的形式规避反射波对波场的影响,如图14所示。边界延长范围d满足下式即可
同时,根据上文介绍的关于单元尺寸的相关要求,延长范围内的单元网格可以划分得足够大。范围内网格尺寸只要小于(D+d)/3即满足理论要求。因此采用此方法并不会过多增加网格数,从而保证了计算效率。考虑地基分层情况下的波场较为复杂,马赫锥锥角θ与土层分布相关,难以通过简单的数学计算获得准确结果,建议在建模过程中通过试算确定。确定d时需要注意由于地基分层引发的多重马赫锥现象。
另外,当运行速度等于瑞利波速时延伸范围接近无限大,式(23)不再适用。由于动应力在地基内部衰减很快,深度方向一般根据地层条件适当选取即可,尽量延伸至基岩面。
5.2.2 纵向空间范围
为了避免由傅里叶变换周期延拓性质带来的虚假反射(如图10所示)对波场的扰动,需要进一步界定纵向空间范围的选取规则,即保证纵向影响区域被全部包括在计算范围L内。如图14所示,其数学表达可以写为
式中δ为由多重马赫锥现象造成的波场纵向延伸距离。
6 结 论
本文论述了內源移动荷载作用下地基响应的基本特点,在此基础上总结了采用2.5D数值模拟技术时计算域选取及网格划分的原则,评价了地基分层对波场的影响及人工边界的波动吸收效果,建议了可以获得无反射波扰动波场响应的建模方法。得到以下几点结论:
(1)考虑高频分量时(15?30 Hz)最大网格尺寸在0.5?1.0 m,模型半宽大于1.5?3.0 m即可满足要求;低频时(0.5 Hz)最大网格尺寸要求可以适当放宽至约20 m,半宽大于60 m即满足要求。建模时可以采用辐射状网格划分,最大网格尺寸满足高频要求,计算域尺寸满足低频要求,同时注意每次向外扩展网格时需要满足“当前计算域尺寸>3倍当前网格尺寸”。
(2)由于现有的人工边界大多在理论上不能满足严格的波动吸收条件,在边界处依然有波动反射现象。当计算域的选择满足低频要求时反射波对计算结果的影响很小。
(3)荷载运行速度小于地基瑞利波速时(v<cR)没有波动传播现象,吸收边界条件对结果没有影响,建议可直接采用固定边界;荷载运行速度大于地基瑞利波速时(v>cR)可以通过切取局部计算域的方式完全规避反射波的影响,此时计算域半宽和纵向空间范围的选取需要遵循与马赫锥锥角和列车全长相关的几何关系。
(4)荷载影响深度内的地基分层会扰乱地基波场,当地基上覆软弱土层或软弱夹层时,波动会在软土层聚集并在加载点后形成多个马赫锥,拉长波场范围。
参考文献:
[1] 陈云敏,边学成.高速铁路路基动力学研究进展[J].土木工程学报,2018,51(06):1-13.
CHEN Yunmin, BIAN Xuecheng. The review of high-speed railway track foundation dynamics[J]. China Civil Engineering Journal,2018,51(06):1-13.
[2] Ling X Z, Chen S J, Zhu Z Y, et al. Field monitoring on the train-induced vibration response of track structure in the Beiluhe permafrost region along Qinghai?Tibet Railway in China[J]. Cold Regions Science and Technology, 2010, 60(1): 75-83.
[3] 蒋红光. 高速铁路板式轨道结构-路基动力相互作用及累积沉降研究[D].杭州:浙江大学,2014.
Jiang Hongguang. Dynamic interaction of slab track structure-subgrade system and accumulative settlement in high-speed railways[D]. Hangzhou:Zhejiang University,2014.
[4] Hu P, Zhang C, Chen S J, et al. Dynamic responses of bridge-embankment transitions in high speed railway: Field tests and data analyses[J]. Engineering Structures, 2018: 565-576.
[5] Shih J Y, Thompson D J, Zervos A. The effect of boundary conditions, model size and damping models in the finite element modelling of a moving load on a track/ground system[J]. Soil Dynamics and Earthquake Engineering, 2016, 89: 12-27.
[6] 巴振宁,王靖雅,梁建文.层状地基中隔振沟对移动列车荷载隔振研究-2.5维IBEM方法[J].振动工程学报,2016,29(5):860-873.
BA Zhenning, WANG Jingya, LIANG Jianwen. Reduction of train-induced vibrations by using a trench in a layered foundation[J]. Journal of Vibration Engineering, 2016,29(5):860-873.
[7] 边学成, 陈云敏, 胡 婷. 基于2.5维有限元方法模拟高速列车产生的地基振动[J]. 中国科学(物理学 力学 天文学),2008,38(5):600-617.
BIAN Xuecheng, CHEN Yunmin, HU Ting. Numerical simulation of high-speed train induced ground vibrations using 2.5D finite element approach[J]. Scientia Sinica Physicsa, Mechanica & Astronomica, 2008, 38(5): 600-617.
[8] Zhu Z, Ling X, Chen S, et al. Analysis of dynamic compressive stress induced by passing trains in permafrost subgrade along Qinghai-Tibet Railway[J]. Cold Regions Science and Technology,2011,65(3): 465-473.
[9] 庄海洋,任佳伟,王 瑞,等.两层三跨框架式地铁地下车站结构弹塑性工作状态与抗震性能水平研究[J].岩土工程学报,2019,41(01):131-138.
ZHUANG Haiyang, REN Jiawei, WANG Rui, et al. Elasto-plastic working states and seismic performance levels of frame-type subway underground station with two layers and three spans[J]. Chinese Journal of Geotechnical Engineering,2019,41(01):131-138.
[10] Yang Y B, Liang X, Hung H H, et al. Comparative study of 2D and 2.5 D responses of long underground tunnels to moving train loads[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 86-100.
[11] 周 彪,谢雄耀,李永盛.基于2.5维有限元算法的边界处理及网格划分[J].同济大学学报(自然科学版),2012,40(10):1463-1468.
ZHOU Biao, XIE Xiongyao, LI Yongsheng. Analysis of boundary treatment and meshing method for 2.5D finite element method[J]. Journal of Tongji University (Natural Science),2012,40(10):1463-1468.
[12] 禹海涛,杨喻声,袁 勇,等.地下结构抗震分析的振动法与波动法对比研究[J].地震工程学报,2019,41(04):845-852.
YU Haitao, YANG Yusheng, YUAN Yong, et al. A comparison between vibration and wave methods in seismic analysis of underground structures[J]. China Earthquake Engineering Journal,2019,41(04):845-852.
[13] 高广运,陈功奇,李 佳.高速列车荷载作用下横观各向同性饱和地基动力特性的数值分析[J].岩石力学与工程学报,2014,33(01):189-198.
GAO Guangyun, CHEN Gongqi, LI Jia. Numerical analysis of dynamic characteristic of transversely isotropic saturated soil foundation subjected to high-speed train load[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(01):189-198.
[14] Liu G R, Jerry S S Q. A non-reflecting boundary for analyzing wave propagation using the finite element method[J]. Finite Elements in Analysis and Design, 2003, 39(5-6): 403-417.
[15] 丁 智,李丹薇,魏新江.基于2.5維有限元方法的列车振动及隔振研究与展望[J].现代隧道技术,2016,53(06):1-11.
DING Zhi, LI Danwei, WEI Xinjiang. Studies and prospects of train vibration and vibration isolation based on 2.5D finite-element method[J]. Modern Tunnelling Technology,2016,53(06):1-11.
[16] Yang Y B, Kuo S R, Hung H H. Frequency-independent infinite elements for analysing semi-infinite problems[J]. International Journal for Numerical Methods in Engineering, 1996, 39(20): 3553-3569.
[17] 王 瑞,胡志平,张亚国,等.黏弹性介质中平、柱面波动传播的应力场及应用探讨[J].岩土力学,2018,39(12):4665-4672.
WANG Rui, HU Zhiping, ZHANG Yaguo, et al. Stress field in viscoelastic medium with propagation of plane and cylindrical waves and the discussion of its application[J]. Rock and Soil Mechanics,2018,39(12):4665-4672.
[18] 谷 音,刘晶波,杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元[J].工程力学,2007,(12):31-37.
GU Yin, LIU Jingbo, DU Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics,2007,(12):31-37.
[19] 宿金成,王幼清.等效动力无限元及其在无限土体模拟中的应用[J].土木工程学报,2013,46(02):131-135.
SU Jincheng, WANG Youqing. Equivalent dynamic infinite element and its application in infinite soil simulation[J]. China Civil Engineering Journal,2013,46(02):131-135.
[20] 孙 莹. 弹性半空间地基无限元动力特性分析[D].西安:西安建筑科技大学,2007.
Sun Ying. Infinite element dynamic property analysis of elastic half-space foundation[D].Xi'an:Xi'an University of Architecture and Technology,2007.
[21] 马龙祥. 基于无限-周期结构理论的车轨耦合及隧道?地层振动响应分析模型研究[D].北京:北京交通大学,2014.
Ma Longxiang. Study on the model of coupled vehicle & track and the analysis model for tunnel-ground vibration response based on the periodi-infinite structure[D].Beijing:Beijing Jiaotong University,2014.
Abstract: In order to improve the solution accuracy and modeling efficiency of 2.5D finite element numerical method, the dynamic response characteristics of ground system under moving load are addressed. The basic rules in selecting computing range and meshing are established. Moreover, the effects of ground stratification on the wave field and wave absorption capacity of boundaries are evaluated. Finally, the modeling approach which can avoid the effect of boundary strictly is suggested. The results indicate that the effect of reflection wave on the results can be overlooked once the computing range fits the requirement of low frequency vibration (about 60 m), and radial mesh can be used in modeling and the minimum mesh size should meet the requirement of high frequency vibration (about 0.5-1.0 m). There is no wave propagation when the moving speed of load is lower than the Rayleigh wave velocity of ground and the fixed boundary is suggested. In addition, the influence of reflected wave can be completely avoided by cutting the local computation range when the moving speed of load is higher than the Rayleigh wave velocity of ground. In that condition, the half-width and longitudinal space range of model should be confirmed following the geometric relation related to the Mach cone angle and the full length of the train. Furthermore, the layered interface at the load influence depth will disturb the wave filed of ground. Wave will accumulate in the soft soil and multiple Mach cones will occur after the loading point when the ground is covered with soft soil or soft interlayer.
Key words: layered ground; modeling; 2.5D finite element method; meshing; absorbing boundary
作者簡介: 王 瑞(1992-),男,博士后,讲师。电话:(029)82337331;E-mail:wr2801100103@163.com
通讯作者: 胡志平(1973-),男,博士,教授。电话:(029)82337356;E-mail:huzhping@chd.edu.cn

