基于改进层次分析法-可拓理论的采空区稳定性评估模型研究*

李强 ，张海云

(1.长沙矿山研究院有限责任公司，湖南 长沙 4101012；2.国家金属采矿工程技术研究中心，湖南 长沙 410012)

0 引言

地下金属矿山在开采矿石的过程中，会遗留大量的采空区，若没有及时充填空区，随着时间的延长，采空区会发生冒落、垮塌等现象，严重威胁矿山的安全生产[1−2]。因此，对采空区稳定性进行评估，对于矿山企业安全生产至关重要。众多学者在采空区稳定性评估方面做了大量研究[3−5]。但由于采空区失稳具有随机性和模糊性特点，且采空区稳定性影响因素较多，因素之间具有不相容性，为评估工作带来难度，采用常规的数学评估模型难以进行准确评估。可拓理论为处理不相容性问题提供理论基础，在风险评估方面应用越来越广泛，取得了较为满意的效果[6−7]。在进行风险评估时，首先需要构建完善的综合评价指标体系，并计算指标权重。当前权重计算主要采用层次分析法，在计算指标权重时评价者对事物认知程度的影响较大，指标权重偏于主观，导致最终评估结果可能与实际情况不符[8]。因此，本文将可拓理论引入到采空区稳定性评估中，采用改进层次分析法确定指标权重，建立基于改进层次分析法-可拓理论的采空区稳定性综合评价模型，并应用到某采空区稳定性评价中，验证模型的有效性。

1 物元可拓计算模型

1.1 确定经典域、节域和评价物元

蔡文提出的物元可拓理论模型为分析处理具有不相容性问题提供了理论依据。该理论以N、C、V三个基本量来表征事物特征，其中N代表事物名称，C为事物特征，V为事物关于特征的量值。其中经典域表示为Rj：

式中，Rj为经典域；Nj代表风险等级；Ci为指标Vji表示第i个指标第j个分级取值范围；aji、bji分别表示各等级取值的上限值和下限值。节域表示为Rp：

式中，Rp为节域；api、bpi分别代表各等级指标取值阈值。

待评对象可以组成物元R：

式中，vi为待评对象各指标取值。

1.2 关联函数的计算

单指标关联度K计算公式为：

式中，Kj(vi)代表各指标关联度；p(vi，Vji)、p(vi，Vpi)分别代表vi与有限区间Vji、Vpi的距离。

1.3 等级判断

在进行综合风险评估时，需要计算综合关联度，即用单指标关联度与权重相乘，得到综合关联度，根据综合关联度计算结果，基于最大隶属度原则，进行风险等级评估。其中，综合关联度计算公式为：

式中，Kj(q)代表综合关联度；wi为指标权重；采用改进层次分析法确定，具体计算过程见文献[9]。

2 模型应用

2.1 构建综合评价指标体系

采空区稳定性受到岩体质量、空区参数、环境等多方面因素的共同影响，因此，采空区稳定性评估是一个多层次复杂的评估过程。在文献[5]和咨询现场技术人员的基础上，选取了岩石抗压强度等14个指标构建了采空区稳定性综合评价指标体系。将采空区稳定性划分为4个等级，即Ⅰ级至Ⅳ级，分别代表稳定性好、极好、一般和差。指标选取情况和等级划分标准见表1。

以文献[5]中所述的某地下铜矿采空区为研究对象，进行稳定性评估，以验证模型的适用性。其中，P1和P2两个采空区的指标取值见表2。

表1 指标风险等级划分情况

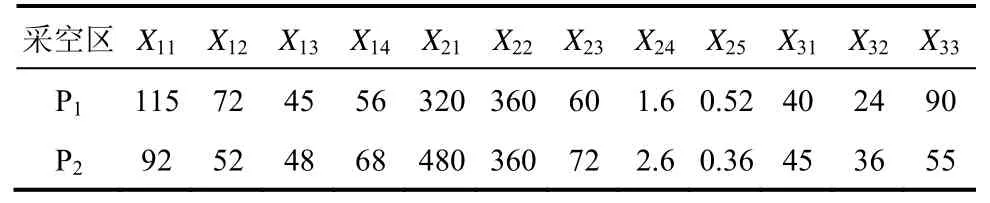
表2 指标参数取值

2.2 指标权重计算

本文采用改进层次分析法确定指标权重。

（1）构建比较矩阵。分别构建准则层O和指标层比较矩阵X1、X2、X3为：

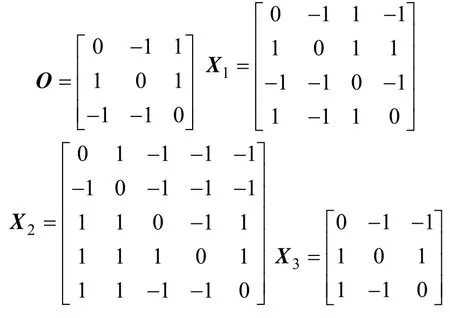
根据改进层次分析法计算方法，分别计算最优传递矩阵和综合判断矩阵，可以得到各层指标权重，计算结果见表3。

表3 指标权重计算结果

2.3 采空区稳定性评估模型计算结果

根据式（4）～式（6），可以计算各采空区各指标的单指标关联度，根据关联度计算结果，可以判断各指标风险等级情况，2个采空区P1和P2的单指标关联度具体计算结果见表4和表5。

根据表4和表5单指标关联度计算结果，可以得到准则层指标关联度，以P1为例，其中X1的指标关联度为：

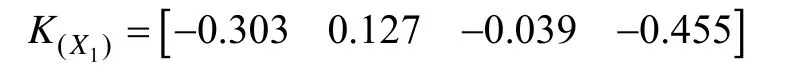
同理，可以得到各采空区准则层指标关联度，计算结果见表6。

根据式（7），可以得到综合关联度，基于最大隶属度原则，判断采空区稳定性等级。为进一步验证所建立的基于改进层次分析法-可拓理论模型的采空区稳定性评估结果的可靠性，与云物元模型[5]和未确知测度计算模型[10]评估结果进行对比，计算结果见表7。

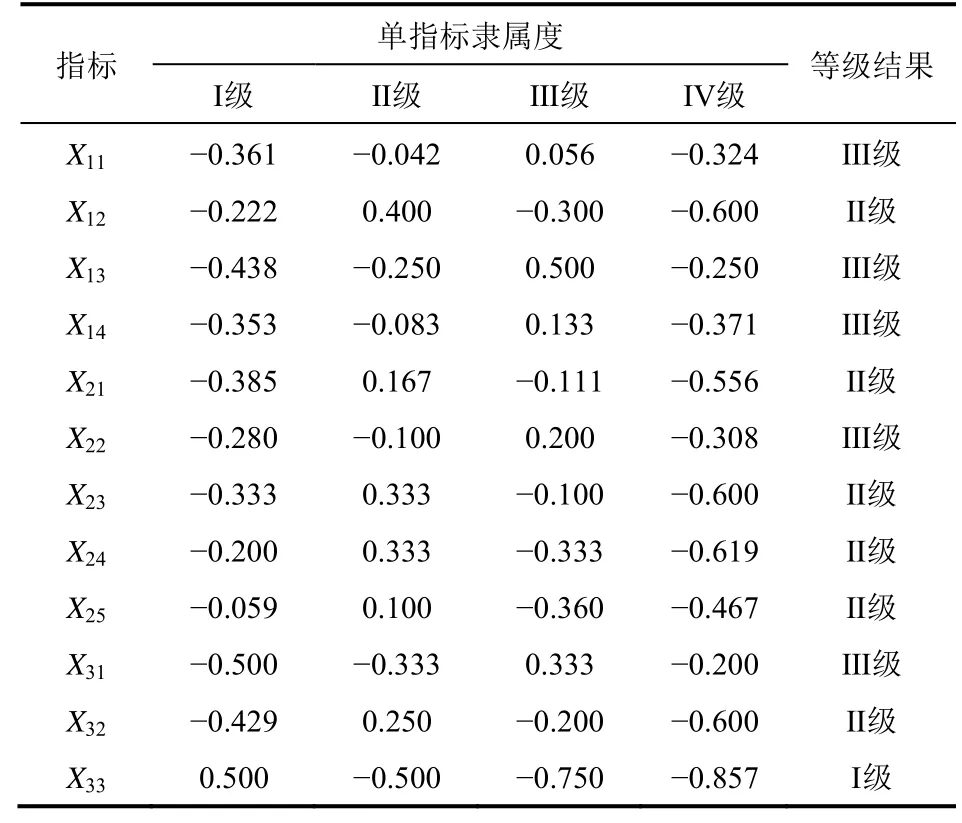
表4 P1单指标关联度计算结果

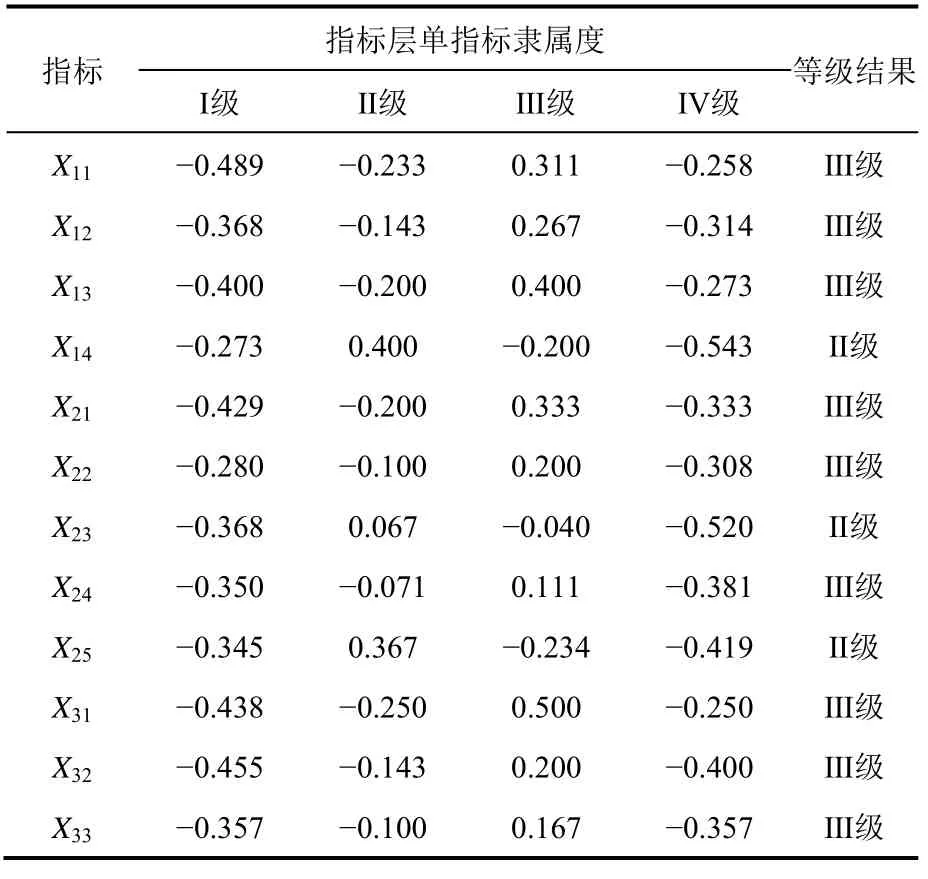
表5 P2单指标关联度计算结果

表6 准则层指标关联度计算结果

根据表7可知，采空区P1和P2的稳定性分别为Ⅱ级和Ⅲ级，即属于极好和一般，与实际情况相符合，暂未发生失稳现象。与云物元模型和未确知测度理论计算模型一致，表明本文所建立的改进层次分析法-可拓理论在采空区稳定性评估方面具有适用性，计算结果合理可靠。

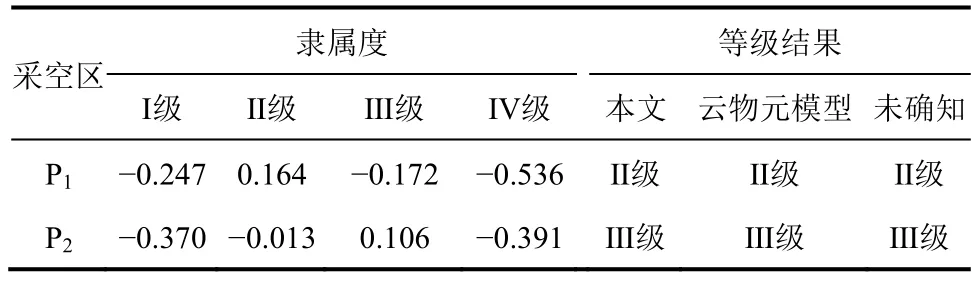
表7 评估结果

3 结论

（1）为克服传统层次分析法在计算指标权重时偏于主观导致评估计算不合理的弊端，采用改进层次分析法确定指标权重，可以提高评估结果的可靠性。

（2）考虑到采空区稳定性评估具有随机性和模糊性特点，且影响因素具有不相容性的特点，将可拓理论引入到采空区稳定性评估中，采用改进的层次分析法-可拓理论评估某采空区稳定性，计算结果合理准确。

（3）采空区稳定性影响因素较多，在今后的研究中，需要进一步完善指标体系，以提高模型评估的可靠性。