页岩气水平井全井筒临界携液流量模型

周朝 何祖清 付道明 罗璇 刘欢乐 孙志扬

1. 中国石化石油工程技术研究院；2. 页岩油气富集机理与有效开发国家重点实验室；3. 中国石化江汉油田石油工程技术研究院

0 引言

多段压裂页岩气水平井在生产早期有大量的压裂液返排到井筒，造成页岩气井长期带液生产，井筒积液问题不容忽视［1］。临界携液流量法是现场普遍采用的积液预测方法，然而，以Turner 模型、Coleman 模型为代表的球状液滴模型对于国内气井的积液预测精度并不理想，考虑液滴变形的李闽模型对于垂直井筒的积液预测精度较高，但是并未考虑井斜变化和产液量对井筒积液的影响［2］。之后，王志彬等［3］、潘杰等［4］考虑液滴变形和产液量，建立了垂直井筒临界携液流量模型，Belfroid等［5］、李丽等［6］、Chen 等［7］考虑井斜角变化，建立了倾斜(水平) 井筒临界携液流量模型。Wang 等［8］根据室内实验数据修正Belfroid 模型，得到考虑井斜和液相流速的连续油管临界携液相关式，但应用条件受限。综合分析，目前的临界携液流量模型均未完整反映页岩气井的复杂井身结构和返排液量变化特征，为此，以液滴模型为基础，综合考虑井筒产液量、液滴变形和造斜率变化，根据变形液滴能量平衡关系，建立了页岩气井全井筒临界携液流量模型。

1 模型建立

1.1 物理模型

以椭球形变形液滴为基础(图1)，推导建立了临界携液流量新模型。液滴从球形变形为椭球形，以单个变形液滴为研究对象，主要进行如下假设：

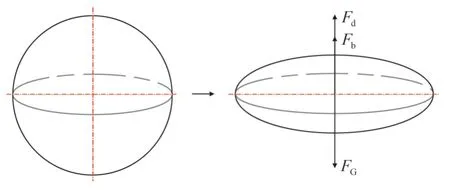
图 1 液滴变形示意图Fig. 1 Schematic droplet deformation

(1)球形液滴以球心所在平面发生对称变形；

(2)球形液滴变形后为光滑的标准椭球体，椭球体的两个长轴长度相等；

(3)气流方向垂直于椭球形液滴两个长轴所在平面；

(4)忽略液滴与气流之间的质量交换和热量交换。

1.2 临界携液流量模型

根据液滴动力学理论，当液滴在气流中保持滞止状态时，作用在液滴上的作用力相互平衡，在垂直井筒中，液滴所受重力等于液滴所受浮力与气体曳力之和，即

代入各个力的表达式，有

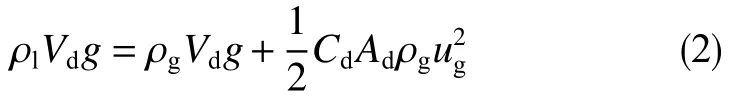
式中，FG为液滴重力，N；Fb为液滴所受浮力，N；Fd为气体曳力，N；ρl为液相密度，kg/m3；Vd为液滴体积，m3；g为重力加速度，m/s2；ρg为气相密度，kg/m3；Cd为曳力系数，无因次；Ad为液滴迎风面积，m2；ug为气相流速，m/s。

液滴从球形变形为椭球形后，式(2)可改写为

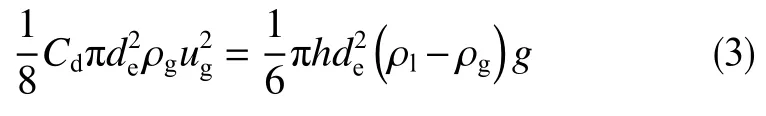
式中，de为椭球形液滴长轴长度，m；h为椭球形液滴短轴长度，m。

根据液滴携液理论，如果气流能将井筒中的最大液滴携带到井口，则气井能够连续携液，此时的气体流速称为临界携液流速［9］。定义椭球形液滴的轴比α为h/de，并考虑临界携液时的最大稳定椭球形液滴长轴长度为dec，则有

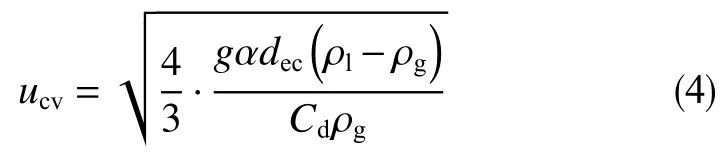
式中，ucv为垂直井筒临界携液流速，m/s；α为椭球形液滴的轴比，小数；dec为最大稳定椭球形液滴长轴长度，m。

根据椭球形液滴轴比实验拟合得到的相关式为［10］

将式(5)代入式(4)整理，得到垂直井筒临界携液流速

在井筒倾斜段和水平段，由于造斜率和井身结构的变化，会影响井筒流体的流动。在造斜率发生变化的地方，液滴与井筒碰撞并反弹，气体及其夹带的液滴的流动方向发生改变，以匹配新的造斜率和井身结构。考虑倾斜段和水平段中液滴与管壁碰撞和反弹造成的能量损失，对垂直井筒临界携液流速进行修正［11］，得到全井筒临界携液流速

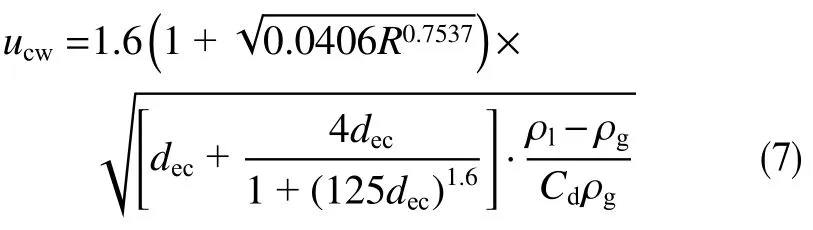
式中，ucw为全井筒临界携液流速，m/s；R为最大造斜率(最大全角变化率)，(°)/30 m。

全井筒临界携液流量为

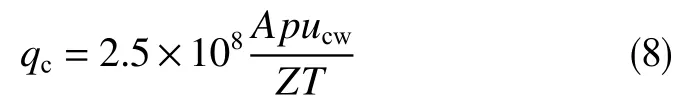
式中，qc为临界携液流量(标况)，m3/d；A为管道横截面积，m2；p为压力，MPa；Z为气相偏差系数，无因次；T为温度，K。

为求取临界携液流量，需首先确定关键参数dec、Cd和表面张力σ，并选取适合的井筒两相流模型。根据式(8)计算出页岩气井井筒各个深度处的临界携液流量后，取各临界携液流量的最大值作为井筒积液判断标准。

2 关键参数确定和模型求解

2.1 最大稳定椭球形液滴尺寸

在环雾流中，液滴在气相湍流作用下向上运动，或者下降形成积液。湍流动能表征了湍流的剧烈程度［12］，气相湍流动能与液滴表面自由能间的平衡关系决定了最大稳定椭球形液滴尺寸。最大稳定椭球形液滴的总表面自由能最小，达到临界积液状态。

2.1.1 最大稳定椭球形液滴总表面自由能

单个最大稳定椭球形液滴的表面积为

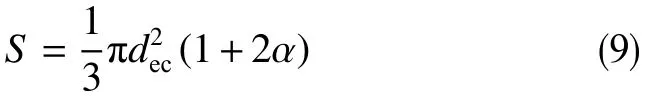
式中，S为最大稳定椭球形液滴的表面积，m2。

表面自由能等于产生表面面积所做的功［13］，则最大稳定椭球形液滴的总表面自由能为

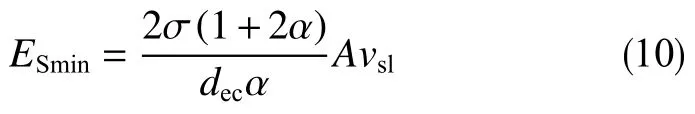
式中，ESmin为最大稳定椭球形液滴总表面自由能，W；σ为气液表面张力，N/m；vsl为液相表观流速，m/s。

2.1.2 气相湍流动能

井筒中单位体积气相湍流动能为

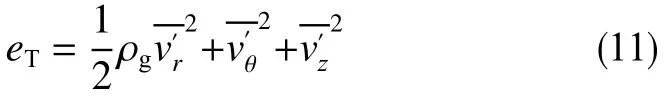
式中，eT为单位体积气相湍流动能，W/m3；v′r为气相湍流平均径向速度脉动，m/s；v′θ为气相湍流平均切向速度脉动，m/s；v′z为气相湍流平均轴向速度脉动，m/s。

由于平均径向速度脉动的均方根近似等于摩擦速度，则有［14］

式中，vsg为气相表观流速，m/s；fsg为以气相表观流速流经光滑管道的气相摩阻系数，无因次。

在环雾流中通常为充分发展的气相湍流流动，可假设气相湍流为各向同性，有v′r=v′θ=v′z，将式(12)代入式(11)，则井筒中气相总湍流动能为［15］

式中，ET为气相总湍流动能，W。

2.1.3 最大稳定椭球形液滴长轴长度

当井筒处于积液的临界状态时，最大稳定椭球形液滴总表面自由能与气相湍流动能相互平衡，并且成正比［15］

其中

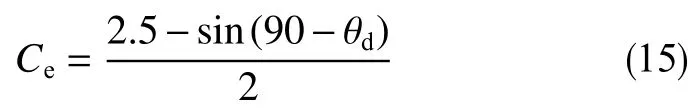
式中，Ce为比例系数，无因次；θd为井斜角，°。

将式(10)和式(13)代入式(14)，可得最大稳定椭球形液滴长轴长度

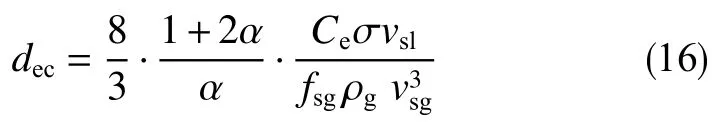
气相摩阻系数可用Blasius 公式计算［16］，对于充分发展的气相湍流流动，雷诺数Re＞2 100，则有

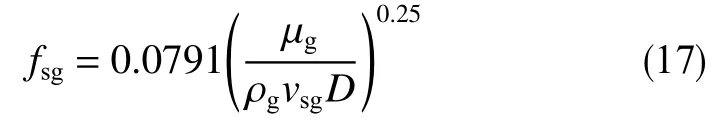
式中，μg为气相黏度，Pa·s；D为管道内径，m。

对于垂直井筒，有Ce=0.75，并考虑到达到最大稳定椭球形液滴时有vsg=ucv，将式(17)代入式(16)整理得

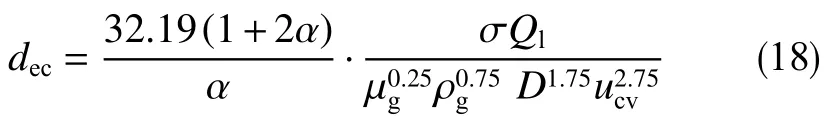
式中，Ql为液相流量，m3/s。

2.2 曳力系数

曳力系数的计算比较复杂，对于球形液滴的曳力系数，可采用Stokes 定律、Newton 公式和标准阻力曲线近似计算［17］。但是，对于椭球形变形液滴来说，其迎风面积与球形液滴相比发生变化，液滴显著变形的情况下，变形液滴的曳力能达到相同条件下刚性球体曳力的两倍以上［18］，因此，球形液滴的曳力系数计算方法对于椭球形液滴不再适用［19］。在井筒高雷诺数条件下，考虑液滴内部流动，对刚性椭球体的曳力系数进行修正，得到椭球形液滴的曳力系数［3］

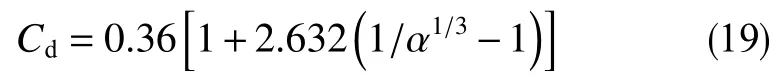
2.3 表面张力

目前的临界携液流量模型中，常取表面张力为常数，但是，表面张力的取值受到液相含量、温度和压力的影响，沿井深是差异分布的，如果取表面张力为常数，会造成临界携液流量计算结果出现偏差，最大偏差可达40%［20］。页岩气井中的液相为返排压裂液，Sutton 公式［21］适用于天然气-盐水体系，能够反映页岩气井产出页岩气和返排压裂液的生产特点，因此选用Sutton 公式计算气-液表面张力

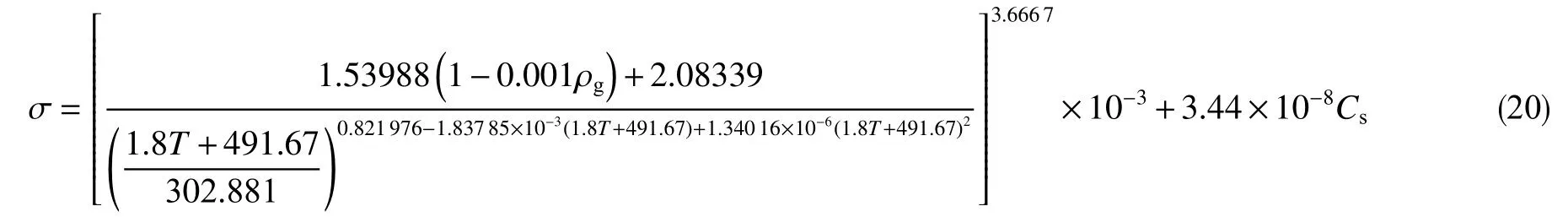
式中，Cs为矿化度，mg/L。

2.4 临界携液流量模型求解

式(7)、式(8)构成了页岩气井全井筒临界携液流量模型，模型中的关键参数dec、Cd和σ分别由式(18)、式(19)、式(20)确定，其中dec和Cd反映了井筒产液量与液滴变形的影响。由于临界携液流速ucw、椭球形液滴轴比α和曳力系数Cd均与最大稳定椭球形液滴长轴长度dec相关，可消去ucw，采用Newton-Raphson 迭代法求解

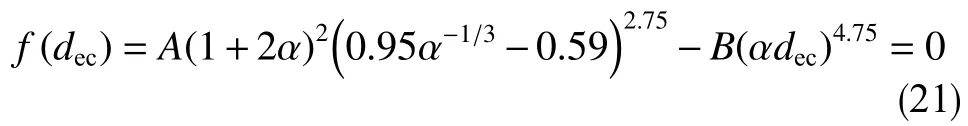
其中

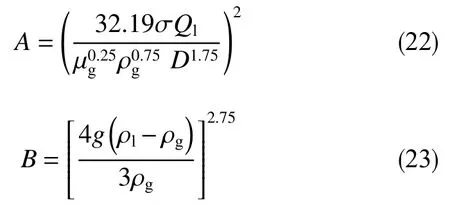
根据式(21)求解出dec后，即可求解出ucw和qc。

2.5 井筒两相流模型优选

临界携液流量受到井筒温压分布的影响，为了准确计算临界携液流量，需要优选适合的两相流模型。由于页岩气水平井井斜角变化较大，因此选取可以计算水平和倾斜井筒压降的两相流模型：Beggs-Brill 模 型［22］、Baker Jardine 模 型［23］、Dulker-Flanigan 模型［24-25］和Mukherjee-Brill 模型［26］。根据涪陵现场39 口页岩气井的实测油(套)压数据和生产数据，分别利用4 种两相流模型计算井底流压，并与实测井底流压结果比较。4 种两相流模型的计算结果如图2 所示，误差分析如表1 所示。可以看出，Mukherjee-Brill 模型的平均相对误差的绝对值和均方根误差均最小，压力计算精度最高，可用于计算页岩气水平井的井筒压力分布，满足现场压力计算精度要求。

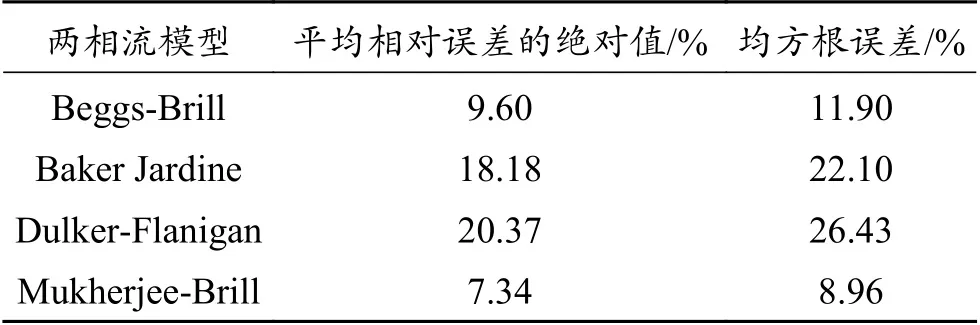
表 1 两相流模型误差分析Table 1 Error analysis of two-phase flow models

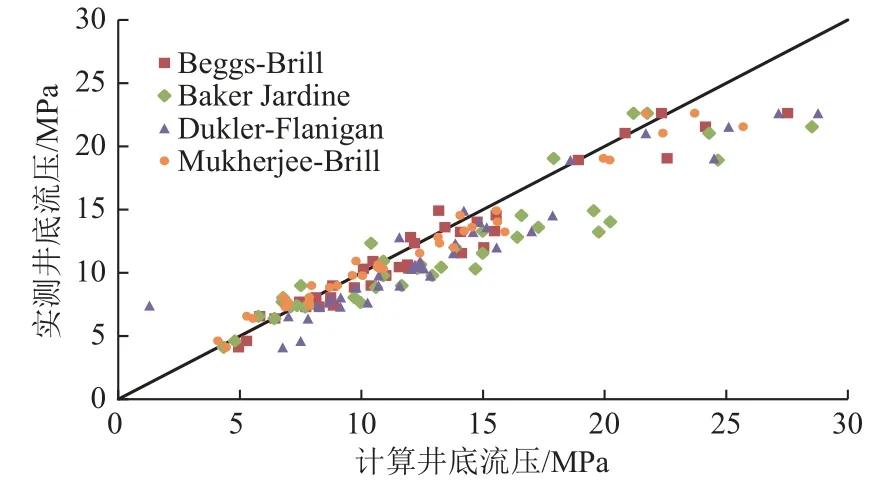
图 2 两相流模型压力计算结果Fig. 2 Pressure calculation result of two-phase flow model

3 应用实例

3.1 现场参数

根据涪陵现场39 口页岩气井的井筒温压测试数据(以最大井筒流压梯度0.45 MPa/100 m 作为积液界限参考［27］)和生产动态数据，得到气井实际积液状态，并选用Belfroid 模型［5］、修正李闽模型［2］、李丽模型［6］、Chen 模型［7］、Wang 模型［8］和本文新模型分别计算现场气井的临界携液流量，根据积液预测精度对新模型进行验证。其中的修正李闽模型是指应用Fiedler 形状函数修正［28］，使模型可应用于倾斜(水平)井筒的积液预测。

Belfroid 模型和修正李闽模型具有类似的表达式

式中，uc为临界携液流速，m/s；C为系数，Belfroid 模型中C取6.6，修正李闽模型中C取2.5；fw为壁面摩阻系数，无因次；NB为Bond 数，无因次。

39 口页岩气井生产数据和实际积液状态如表2所示。天然气相对密度0.56~0.57，返排液密度1.01~1.05 g/cm3，油管内径为62 mm 或50.6 mm，套管内径为115 mm。采用Yarborough-Hall 方法［29］计算气相偏差系数。

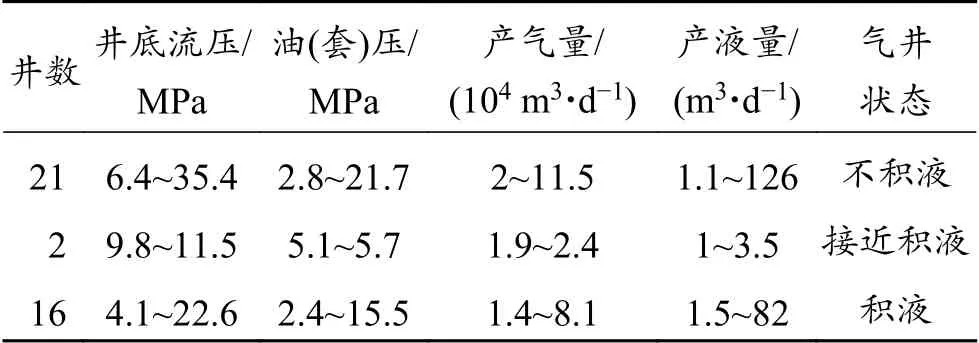
表 2 页岩气井生产数据和积液状态Table 2 Field parameters of shale gas wells

3.2 积液预测结果分析

根据表2 的页岩气井现场参数，以及各井的井筒温压分布数据，分别用6 种临界携液流量模型计算全井筒临界携液流量，并取所有临界携液流量中的最大值与实际产气量进行比较，判断井筒积液状态。6 种模型的积液预测精度和预测结果如表3 和图3 所示，图3 中的对角线左上方区域表示气井不积液，右下方区域表示气井积液，而处于接近积液状态的气井，其数据点应位于对角线±15% 偏差范围内［4］(两条虚线之间的区域)。将6 种临界携液流量模型的积液预测结果与井筒实际积液状态比较，得到各模型的积液预测精度。

由表3 和图3 可知，对于页岩气水平井的积液预测，Belfroid 模型的预测结果偏差最大，Belfroid 模型和Wang 模型均高估了临界携液流量，因此这两种模型可以准确预测积液井，但是对不积液井的预测误差较大；修正李闽模型低估了临界携液流量，因此可以准确预测不积液井，但是对积液井的预测误差较大；李丽模型和Chen 模型对于各种积液状态井的预测结果均有偏差；新模型的积液预测结果与实际积液情况的符合率最高，总体积液预测精度达92.3%，新模型可以准确预测积液井和接近积液井，只是对3 口不积液井的预测结果出现偏差，尽管如此，新模型对不积液井的预测精度仍然能够满足现场应用需求。综合来看，新模型对于页岩气水平井的积液预测精度最高，可以有效指导现场积液判断与排采工艺选择。

4 结论

(1)依据液滴动力学分析和能量分析，综合考虑井筒产液量、液滴变形和造斜率变化引起的液滴能量损失，根据变形液滴能量平衡关系，建立了页岩气井全井筒临界携液流量模型，弥补了现有模型没有同时考虑页岩气水平井复杂井身结构和返排液量变化的缺陷。

(2)根据变形液滴能量平衡关系，确定了最大稳定变形液滴长轴长度；选取了适用于页岩气水平井的曳力系数公式和表面张力公式；优选Mukherjee-Brill 两相流模型用于计算页岩气水平井的井筒压力分布，均方根误差为8.96%，能满足现场压力计算精度要求。

(3) 39 口页岩气井的实例分析表明，与现有临界携液流量模型相比，新模型对于页岩气水平井的积液预测符合率最高，积液预测精度达92.3%，新模型可以有效指导页岩气水平井积液判断。