基于Fluent 的水下采油树本体流动与传热特性分析

王莹莹 刘书杰 王名春 杨进 程子云 杨红飞

1. 中国石油大学(北京)安全与海洋工程学院；2. 中海石油(中国)有限公司海南分公司；3. 中海油研究总院有限责任公司

0 引言

随着深水油气资源不断发现［1］，水下生产系统因能够避免海面恶劣环境的影响，后期操作灵活，相较浮式平台造价较低、受政策影响小等优点，已经成为海洋油气开采中的关键开发模式。水下采油树是水下生产系统的核心装备之一，对水下油气开采起着关键的控制作用。目前，水下采油树的关键技术 仍 大 部 分被FMC Technologies、One Subsea、GE、Dril-Quip、Aker Solutions 等国外知名油气公司垄断。我国针对水下采油树的研究起步较晚，但随着中国海洋石油集团有限公司在浅水和深水采油树国产化关键技术领域的持续研究攻关和创新引领，一系列具有自主知识产权的核心技术实现突破，以威飞、重庆前卫、江钻、宝鸡、美钻等为代表的国内知名海洋装备公司，初步具备了水下采油树国产化的加工和制造能力，我国水下采油树国产化工程有望在渤海和南海率先推进。

水下采油树在正常的生产工况下，内部流体的温度很高，而外部海水的温度很低，热量在不断向外散失。同时，节流阀处不同的入口速度和入口压力都会对油气的流动产生影响。在停产后，内部油气停止流动，随着时间的延长，当内部流体温度下降到临界温度时，在流道内可能会生成天然气水合物，从而阻碍管线内部流体的流动，严重时会发生堵塞，造成安全事故。因此，研究水下采油树本体在正常生产状态和停机状态的流动与传热特性，对于提高水下采油树安全可靠性具有重要的意义。国内外针对水下采油树流动和传热的研究较少［2-3］。2012 年丁矿等［4］对水下采油树连接器进行热分析和隔热计算，得出需要对连接器进行保温设计；2015 年秦蕊等［5］对水下采油树流道进行热应力分析，得出在正常生产中应采取隔热措施降低水下采油树的热应力；2015 年B. HU 等［6］通过CFD 方法对水平海底采油树组件的稳态传热特性进行了分析，研究了海底采油树组件的对流传热和海底树周围的流动特性，最终获得了流经海底采油树的冷海水的特性，以及海底采油树与环境冷水之间的对流换热特性，证明了这些热点具有较高的对流换热系数(CHTC)，并产生大量的热损失；2016 年B. HU 等［7］对水下闸阀进行传热分析，得出在受流场影响的迎风表面和背风表面上，温度和对流传热系数的分布都不同；2020 年P. LIU［8］提出了一种基于动态贝叶斯网络(DBN)的海底XT 故障诊断方法，并研究了海底XT 系统的3 个故障诊断案例，最终得出结论：3 个故障诊断案例验证了该方法的准确性和有效性，且该方法适用于向工程师提供维护说明；2013 年刘昌领等［9］对1 500 m 水深、温度等级U 级、设计压力69 MPa 的采油树输油管道单层保温和双层保温的保温效果和保温材料单位体积总费用进行对比计算，结果发现双层保温设计更经济合理；2014 年吕欢欢等［10］对水下卧式采油树传热特性进行分析，得出采油树温度分布以及出油管内壁温度随时间的变化规律，和不同原油温度、海水温度条件下保温层厚度和冷却时间的关系；2015 年张鹏举等［11］对水下采油树进行流场分析,得出水下采油树本体内部流体压力和速度变化较均匀，只是在变径处或直角弯管处会出现湍流现象，温度变化比较均匀；2015年赵旭东等［12］对水下采油树系统内部管道进行传热数值模拟，最终得出结论：原油须以一定速度流经管道才可以避免温度下降过快，并将边缘将要成核或已经成核但尚未成团的水合物带走。

笔者针对1 500 m 水深水下采油树的本体传热特性进行了分析，通过建立水下采油树与内部流体耦合流动和传热模型，分析计算稳态状态下不同压力和入口流速下流道流体的流动情况，同时通过改变流道的尺寸，计算盲管段长度对流动的影响，得出了不同流道结构及输入参数下流体的流动规律，计算结果对水下采油树流道结构设计和流体入口参数的控制具有一定的指导意义。同时，针对关井8 h油气停输工况进行耦合模型的非稳态工况模拟分析，探寻不同海水温度、流体入口温度条件下的流道温降情况，分析水下采油树本体流道是否能够达到水合物生成的临界状态。同时，对水下采油树本体进行了保温计算，得出了不同保温层厚度下流体的冷却曲线，确定了水下采油树是否需要添加保温层的判定方法，为实际水下采油树本体保温层的设计提供参考。

1 水下采油树与海水对流换热系数的确定

水下采油树主要由水下采油树本体、井口连接器、导向基座、油管悬挂器、采油树内帽、顶部阻塞器、岩屑帽、SCM 水下控制单元、采油树框架、配重阳极块、操作面板以及相关阀门管道等部分组成，结构示意图见图1。

图 1 水下采油树结构Fig. 1 Structure of subsea christmas tree

该水下采油树主要应用于南海某气田，在生产工况下，由于流体高速流动，热量散失的天然气由流入的天然气补充，内部流道流体温度几乎不变，传热过程为高温流体与油管挂对流换热、油管挂与采油树本体热传导、本体与外部海水对流换热。当生产系统处于停修井工况时，采油树内部天然气停止流动。此时采油树内部充满一定压力的天然气，流道入口和出口都关闭，外部海水温度恒定。随着采油树温度的降低，采油树内部流道逐渐冷却，压力不变的情况下，当温度降到水合物临界温度时，极易形成天然气水合物。水合物的生成会导致井下油管、油管挂、输油管线内压降增大，严重时堵塞井筒、管线、阀门和其他设备，影响水下采油树的正常生产。

为了简化计算模型，将水下采油树与海水接触的外表面设置成对流换热边界条件，可以省略海水域模型。通过Fluent 对比理论得出水下采油树本体外表面与海水之间的对流换热系数，计算公式可表示为［10］

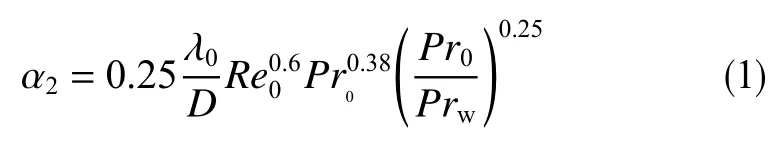
式中，λ0为海水导热系数，W/(m·K)；D为管路外径，m；Re0为海水流动雷诺数；Pr0、Prw分别为远离管壁和靠近管壁海水的普朗特数。根据文献［10］，原油温度50~120 ℃范围内，海水温度分别为5、10、15、20 ℃时，采油树本体外部与海水对流换热系数可近似按489、471、452、445 W/(m2·K)计算。

外部对流换热系数主要受到水下采油树外形结构的影响。笔者分别建立了水下采油树和外部海水模型，如图2 所示将各个接触面分别设置成耦合接触面。定义海水温度4 ℃，流体温度57 ℃。为了更准确地计算出水下采油树外壁面的换热系数，细化与外部海水接触的采油树外壁面的网格。

图 2 外壁面换热系数计算模型Fig. 2 Calculation model of external wall heat transfer coefficient

提取中性面上的速度和压力分布，如图3 所示。可以看出，上下区域不与水下采油树接触的流体速度始终保持为0.3 m/s，中间与水下采油树接触的流体在冲击采油树后速度降低，产生一个背压区，并且在采油树背面的流体速度减小，从而得到水下采油树本体与海水流固耦合壁面的对流换热系数440 W/(m2·K)，与文献［10］相符。

图 3 流域内速度和压力分布Fig. 3 Velocity and pressure distribution in the field

2 本体稳态耦合传热分析

2.1 本体传热模型

水下采油树本体传热系统模型主要包括海水层、采油树本体、油管悬挂器和内部流体，计算中海水域必须足够大才能获得准确的结果，大大增加了计算的复杂性。为方便分析，对模型进行简化，如图4 所示，实际计算中忽略海水域的模型，将采油树本体外表面与海水接触部分设置成对流换热边界条件，可大大简化模型计算复杂性。

2.2 参数确定

以我国南部某气田为例进行分析，该气田天然气组分摩尔分数如表1 所示。根据该天然气组分计算天然气的热导率、密度、定压比热容和黏度等热物性参数。

表 1 天然气组分Table 1 Natural gas composition %

2.2.1 热导率

热导率计算参考文献［13］，加压下纯态气体的热导率计算公式为

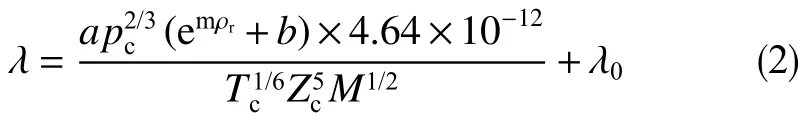
式中，pc为气体临界压力，Pa；ρr、Zc分别为纯态气体的相对密度和临界压缩因子；a、b、m为气体常数，数值见表2；Tc为气体临界温度，K；Mi为气体摩尔质量，g/mol；λ、λ0分别为加压和常压下气体的热导率，W/(cm·K)。

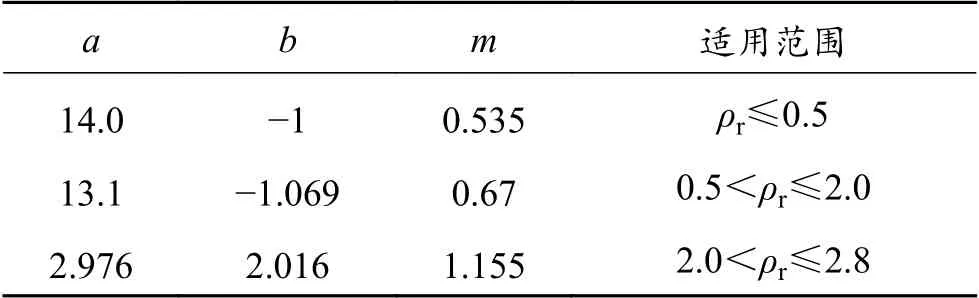
表 2 气体常数数值Table 2 Gas constant values

加压下混合气体热导率的计算，先按纯气体求出每一组分的热导率，再按相应摩尔比例的线性组合叠加法求得混合气体的热导率。

2.2.2 密度

根据混合态流体的热物理性质，首先计算理想状态气体混合物的平均摩尔质量，高压下混合气体相对密度近似按照理想气体状态方程进行估算。

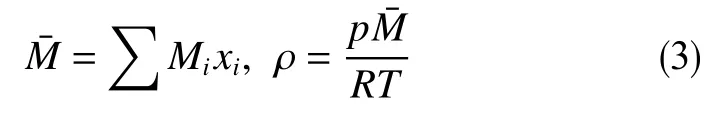
式中，xi为i组分的摩尔分数；为混合气体的摩尔质量，g/mol；p为混合气体压力，Pa；R为气体常数；T为混合气体温度，K；ρ为混合气体密度，g/cm3。

2.2.3 比热容

根据文献［14-15］，混合态气体的定压比热容可由以下拟合公式(4)计算。

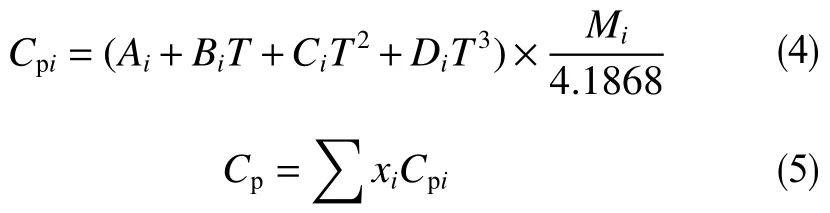
式中，Cpi为i组分气体定压摩尔比热容，J/(mol·K)；Ai、Bi、Ci、Di分别为纯态气体比热容方程常数，具体数值可以查阅文献［11］附录B；Cp为混合气体定压摩尔比热容，J/(mol·K)。

2.2.4 黏度

黏度计算参考文献［16］，采用Thodos 法计算带压混合气体的黏度。首先计算加压状态下纯态气体黏度，计算公式为

式中，μi为加压下i组分气体的黏度，mPa·s；μ0i为同温度、常压下i气体的黏度，mPa·s；c、d、n为气体常数，数值见表3，表中Tr为相对温度，是实际温度与绝对温度的比值。

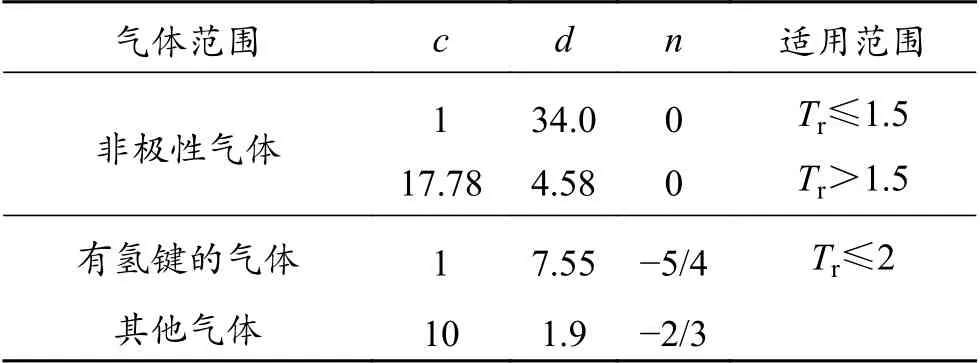
表 3 Thodos 法气体常数值Table 3 Gas constant values by Thodos method

如果已知各组分加压下的黏度，可用式(7)计算加压下气体混合物的黏度，但各组分的压力应取系统总压，而不是各组分的分压。式(7)第1 项为常压下混合气体的黏度。

其中

式中，μi、μj分别为组分i、j的带压气体黏度，mPa·s；Bij为i、j组分相互作用系数；μp为带压混合气体黏度修正参数，mPa·s；pcm为混合气体虚拟临界压力，Pa；Tcm为混合气体虚拟临界温度，K；ρrm为混合气体相对密度。

本体和油管悬挂器材料为2 1/4Cr-1Mo，根据计算确定的天然气和本体及油管悬挂器热物性参数如表4 所示。

表 4 天然气及本体-悬挂器热物性参数Table 4 Thermophysical parameters of natural gas and body hanger

2.3 传热分析

从外至内分别建立的采油树本体-油管悬挂器-内部天然气流体相互耦合的热流计算模型，包括2 个固体域(采油树本体、油管悬挂器)和1 个流体域(内部天然气气体)。实际内部天然气、海水的热物性参数是随温度变化的，这里忽略热物性参数随温度和压力的变化。

水下采油树为非对称模型，所以实际计算中直接建立了三维实体模型进行分析，简化倒角、小孔等非必要实体特征，整体划分为四面体结构网格，分析模型如图5 所示。

图 5 Fluent 计算网格模型Fig. 5 Fluent computing grid model

各计算域的网格单元均采用QUADS 类型，在GAMBIT 里完成结构化网格的创建。在计算过程中采用网格自适应技术，通过温度梯度和速度梯度对网格进行调整，完成对局部网格的细化，优化计算结果。对计算区域采用有限容积法在同位网格上进行控制方程的离散，采用SIMPLE 算法处理速度和压力的耦合，对流项采用二阶迎风格式，扩散项采用中心差分。计算中采用整场离散、整场求解的方法，把固体和流体中的传热问题统一处理；同时，考虑到在流固耦合界面流动变化剧烈并存在黏性底层，选用标准壁面函数处理流动边界层和传热边界层。为保证计算结果的网格独立性，进行了网格独立性的考核，其标准为相邻2 个计算中最高温度的相对比值不超过1%。在这个条件下保证计算精度和计算量的平衡。选取相邻2 个迭代步之间的最大动量和能量的残差相对变化率小于10-5为计算的收敛条件。

定义初始参数：天然气流道入口流速为4.2 m/s，入口温度57 ℃，入口压力8 MPa，外部海水4 ℃时，通过Fluent 计算得到流体在本体流道内的流动和传热情况如图6 所示，可以看出，流道内的压力几乎没有变化；采油树本体在与流体接触的部分温度较高，其余大部分区域都是接近海水温度4 ℃；在盲管段由于气体集聚速度几乎为0，在T 型通道拐角处上端速度达到最大值，下端速度减小，入口速度为4.2 m/s，拐角上端最大速度达到7.2 m/s。

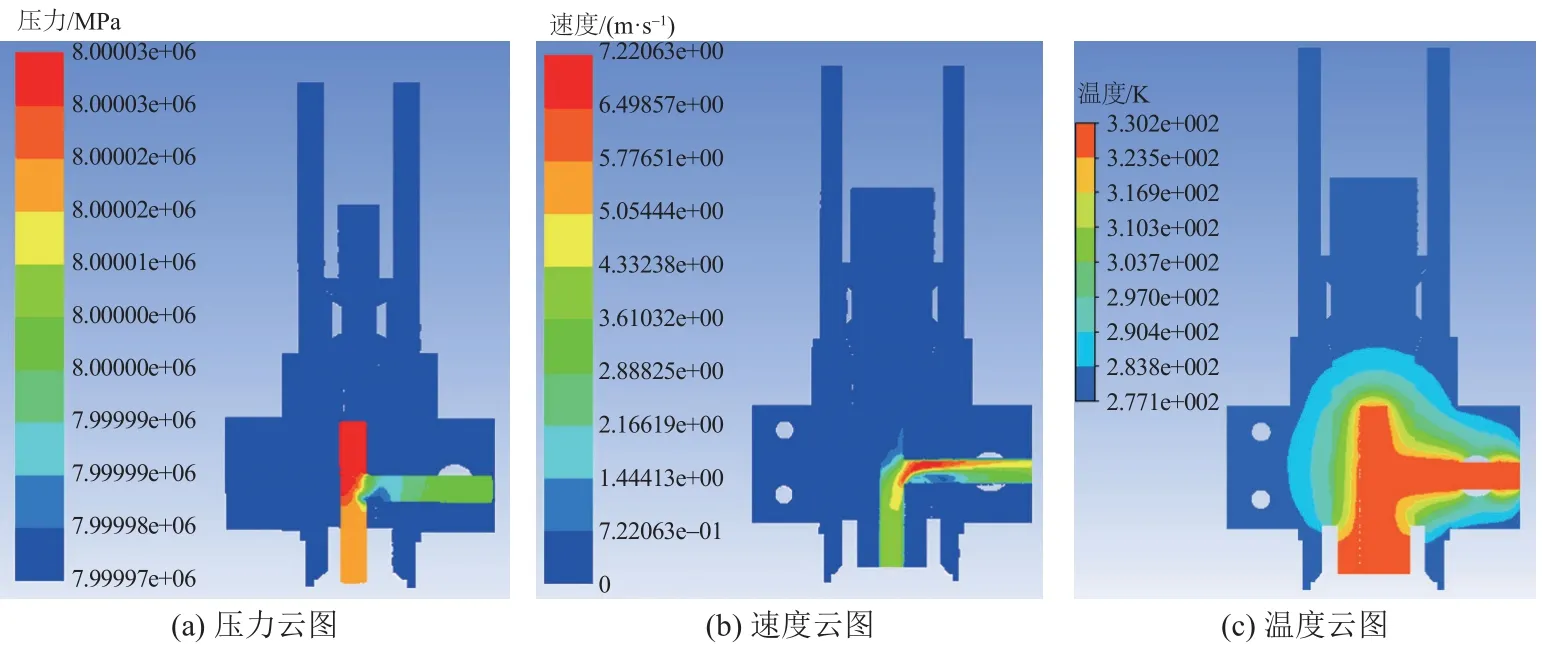
图 6 本体流道内流体流动特性云图Fig. 6 Cloud diagram of fluid flow characteristics in body channel

2.4 参数分析

保持入口流速、入口压力和流道结构尺寸不变，在稳态分析条件下，通过改变海水温度，入口天然气温度，分析其对天然气流动和传热的影响。分别取海水温度4、10、15、21 ℃，流体入口温度57 、70 、85、100 、121 ℃，得到不同海水温度和入口温度下流道内天然气的流速和温度情况。从图7 可以看出，当天然气在采油树本体流道内流动时，天然气的入口温度和外界海水温度对流体的流动速度几乎没有影响；天然气在流道内的温度受入口温度和外界海水温度的影响较大，且几乎呈线性影响；当天然气与海水温度差较大时，天然气入口温度每升高15 ℃，流道内天然气平均温度能升高9 ℃；海水温度每升高5 ℃，流道内天然气平均温度能升高2.5 ℃。

图 7 不同海水温度下流体流动特性与流体入口温度关系Fig. 7 Relationship between fluid flow characteristics and fluid inlet temperature at different seawater temperatures

本体内流道如图8 所示，原始尺寸为L1=534 mm，L2=318 mm，L3=670 mm，R=135 mm，保持入口温度为57 ℃，海水温度4 ℃，入口压力8 MPa，控制入口流速4.2 m/s 不变，改变盲管段L2的长度，长度分别设计为208 、268、318 mm(原始长度)，368 mm，得出流体流动特性与盲管长度的关系。从图9 可以看出，盲管L2越长，内部天然气的平均流速和最大流速都越小，说明盲管不利于流体流动；盲管长度对天然气平均温度几乎没有影响。

控制盲管长度318 mm 不变，改变入口流速4.2、3.2、2.2、5.2、6.2 m/s，得到内部流体流动特性随入口速度的变化规律。从图10 可看出，天然气在流道内流动的平均速度和最大速度都随入口速度增大而增大，几乎是正比关系；入口速度每增大1 m/s，平均速度增大0.45 m/s，最大速度增大1.7 m/s；流体平均温度随入口速度增加而增大，但是增大幅度很小，速度每增加1 m/s，平均温度增加大约0.5 ℃。

图 8 采油树内部流道示意图Fig. 8 Schematic diagram of internal flow channel of christmas tree

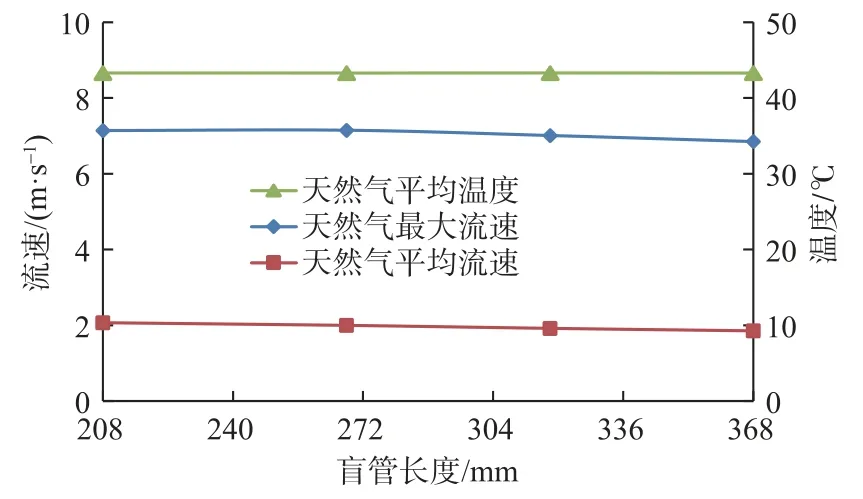
图 9 盲管长度对流体流动特性的影响Fig. 9 Influence of blind pipe length on fluid flow characteristics

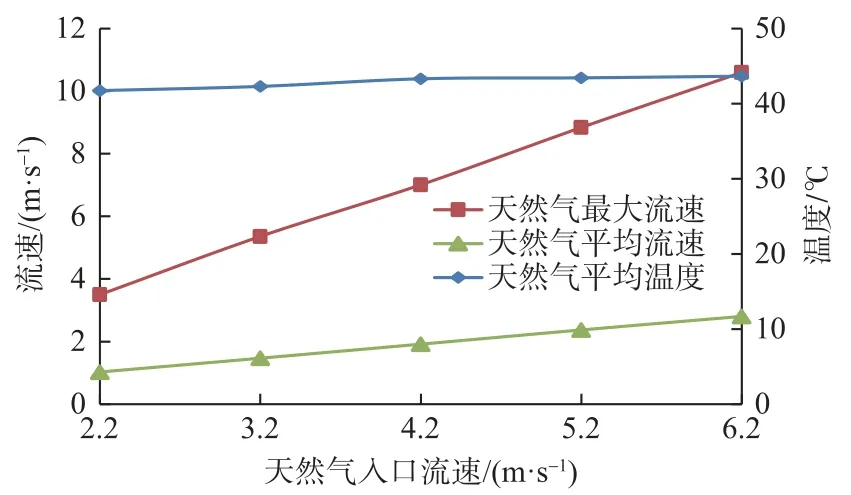
图 10 流体流动特性与流体入口流速的关系Fig. 10 Relationship between fluid flow characteristics and fluid inlet velocity

3 非稳态耦合传热

稳态传热主要是针对油气在流道内的高速流动状态进行分析，得到不同参数下的流动状态。而非稳态传热以稳态传热的最终状态为起始，主要研究在油气流体停止流动状态下，由于结构热传递导致的温降规律，并通过温降规律对水下采油树进行保温设计，防止温度过低形成水合物。

适用于深水水下结构物的保温材料主要有Trelleborg Offshore、FMC、BOE 开发的固体聚氨酯、弹性体及聚氨酯、环氧树脂、硅树脂等为基体的复合泡沫保温材料。选用环氧树脂复合泡沫作为采油树保温材料［17］，该材料密度700~800 kg/m3，热导率0.12~0.17 W/(m·K)，比热容1 500~1 800 J/(kg·K)，最大湿式服务温度60~115 ℃，最大服务水深300 m。

在停机工况下，流道流体停止流动，由于内部高温流体与外部低温海水之间的换热导致内部流体温度急剧下降，同时由于流道内天然气压力为8 MPa，达到了天然气水合物形成的临界条件，因此必须对水下采油树进行防止形成天然气水合物设计。基于稳态计算结果，将天然气流道的入口和出口关闭，对模型进行非稳态耦合传热分析，模拟在停止流动过程中天然气流体平均温度随时间下降的规律，模拟停机时间为8 h，计算工况为天然气入口温度57 ℃，入口速度4.2 m/s，入口压力8 MPa，外部海水温度4 ℃。水下采油树外表面全覆盖保温层模型如图11 所示，分别取保温层厚度为5 、10 、15、20 mm 进行对比分析，得到内部流体平均温度随时间变化曲线。从图12 可看出，停机初始阶段流道内天然气的温度急剧下降，500~10 000 s 时段下降趋势开始放缓，10 000 s 之后温度下降速率逐渐稳定。

图 11 保温层计算模型Fig. 11 Calculation model of insulation layer

图 12 不同保温层厚度时流体非稳态温降Fig. 12 Unsteady temperature drop of fluid with different insulation layer thickness

图13 为不同厚度保温层下采油树流道内天然气在停机开始(流动状态时)和停机最终(停止流动8 h)的平均温度情况，可以看出，当天然气处于流动状态时，保温层越厚，天然气平均温度越高，而且是近乎于线性关系。当停机8 h 后，保温层越厚，天然气最终温度越高，无保温层时天然气最终温度降低到接近4 ℃，保温层厚度为20 mm 时最终温度可以保持在14 ℃。在8 MPa 压力条件下，目标气田形成水合物的临界温度为284 K［18］，所以在进行保温设计时，必须保证天然气温度大于284 K，图中11℃对应的最优的保温层厚度为16 mm。

4 结论

(1)水下采油树本体流道内气体的压力与入口压力一致，无明显压降，内部流体温度分布均匀。采油树本体在与流体接触的部分温度较高，其余大部分区域都接近海水温度。在盲管段由于气体集聚速度几乎为0，在T 型通道拐角处上端速度达到最大值，下端速度减小，拐角一定程度上不利于流体流动。

(2)入口温度和外界海水温度对流体的流速没有影响，对流体的温度影响呈线性规律。盲管长度越大，流道内天然气的平均流速和最大流速越小，盲管长度对流道内天然气的平均温度没有影响。天然气在流道内流动的平均速度和最大速度都随入口速度增大而增大。为保证流体流动效率、入口流速大，入口温度高，设计时盲管长度应适当减小。

(3)水下采油树本体非稳态传热时，停机初始阶段流道内天然气的温度急剧下降，后下降趋势开始缓和，最终变缓。在本文计算工况下，水下采油树停机8 h 达到水合物生成的临界条件。研究形成了水下采油树保温层计算的一般方法，得到了水下采油树最优的保温层厚度。