具有修正策略的改进NSGA－II 三维路径规划

封建湖，郑宝娟，封 硕，张婷宇

（1.长安大学理学院，陕西 西安 710064；2.长安大学工程机械学院，陕西 西安 710064）

1 引言

路径规划是机器人定位与导航领域研究的热点问题之一，目前的路径规划方法如蚁群算法，粒子群算法，蜂群算法，萤火虫算法及混合算法等[1-3]多用于二维平面空间规划。在复杂环境下三维空间的机器人路径避障问题越来越受到学者们的关注。例如，文献[4]提出了一种结合人工势场思想的改进蚁群算法并用于三维路径规划，并将路径的长度作为优化准则，但是只优化了路径长度，实用性不高。文献[5]提出在偏微分高程建模下蚁群算法的三维路径规划方法，但计算结果容易陷入局部最优。

遗传算法根据生物进化过程的自然遗传理论构造的随机搜索算法，其优点是并行计算能力强，鲁棒性和全局收敛性好，已经成功地应用于机器人的路径规划问题。对多目标的遗传算法，文献[6]改进了非支配排序遗传算法（NSGA），提出了复杂度更低，更能保持种群多样性，具有Pareto 占优的NSGA-II 算法。文献[7]考虑路径长度和难度，加入修正算子减少冗余路径，从而改进NSGA-II 算法并成功应用于二维路径规划，取得了很好的效果。文献[8]在二维空间中优化了路径长度、路径安全性和路径平滑度，在NSGA-II 算法的基础上加入辅助选择算子，并证明了辅助选择算子使算法得到的Pareto 解更优，但对冗余路径情况和路径能耗未做考虑。

针对以上算法的优势和不足，尝试基于NSGA-II 算法研究三维多目标路径规划，首先，构造复杂的三维曲面空间并栅格化；其次考虑路径长度，能耗，路径起伏等优化因子，建立多目标优化函数；最后基于文献[7-8]的改进成果，对NSGA-II 算法进行改进，在选择算子中加入辅助选择算子，得到更优的Pareto 前沿解集，设计多种路径优化的遗传算子，加快搜索能力，使其更好地应用到路径规划问题上。

2 规划空间的构造

2.1 地形构建及栅格化处理

使用栅格表示的方法，根据机器人的尺寸，将三维曲面空间离散成若干的栅格，建立笛卡尔坐标系，每个栅格都对应一个点坐标（xi，yi，zi），如图1（a）所示。xy 代表水平地理坐标位置，z 代表地形地貌的高度（在栅格化的过程中对z 进行取整），实际应用中如果细化网格，将能逼近三维地形地貌。采取降维的思想，将三维地形表面分解为二维平面和高度变化的集合，从而简化三维空间的搜索难度，加快搜索能力。灰色代表有高度信息的自由栅格，黑色代表障碍栅格，障碍物数目，位置，大小已知，离散化后将高度信息z 标注于相应栅格上，反应机器人在经过不同栅格时的高度变化，如图1（b）所示。

图1 建立的三维规划空间Fig.1 The Established Three-Dimensional Planning Space

2.2 适应度函数的建立

文献[9]用栅格高度值代表能耗，对上下坡能耗变化不同未分类讨论，有一定缺陷。在三维路径规划中实现的目标有：在环境静态、地图有界、障碍物已知、起点和终点已知的条件下，机器人行走路径长度最短，上下坡总能耗最小，减少上下坡的起伏，且每条路径都规避障碍物。

其中，gi路径中第i 段相邻两点的能耗值，为了更加贴近真实设备上下坡所耗能量不同的状况，将上坡和下坡进行差异化分析，简单起见，文中只对上坡动作和下坡动作乘以不同的权重系数，考虑到下坡省力，上坡费力，对上坡和下坡分段处理：

（4）障碍物的规避采用约束条件来表达，将障碍物点的集合记为O=（o1，o2，…ok）则规划的路径点pi不能取集合O 中的点，且线段pipi+1不能穿过点集O。

3 改进NSGA-II 的多目标路径规划

3.1 传统多目标遗传算法

针对以上规划空间及优化目标函数，选择NSGA-II 算法来解决多目标函数路径优化问题，对多目标函数的优化，传统的遗传算法是将多目标函数加权组合成单目标函数来处理，需要不断调整权重参数来得到近似最优解，往往不能很好地解决实际问题。智能的多目标优化算法是找到Pareto 占优解，NSGA-II 算法是目前解决多目标遗传算法影响大，应用范围广的优化算法之一[10]，突出优点是快速非支配排序的方法，且得到的解具有多样性和均匀性。文献[7-8]将NSGA-II 算法成功地应用到了二维路径规划问题上，然而对三维栅格路径规划问题的应用比较少。基于文献[7-8]的研究成果，考虑路径规划结果的连续性，快速收敛性和Pareto 最优，对NSGA-II 算法进行改进，改进的遗传算法包括以下编码方式和遗传算子的设计，其中在具有非支配排序的选择算子中加入辅助决策算子及修正算子的设计颇为关键。

3.2 改进NSGA-II 算法

3.2.1 编码及初始种群的产生

m×m×m 规格地图下，采用栅格序号编码，并与坐标法相结合。每一个栅格降维后分解为（xi，yi）和高度zi的集合。对降维后的空间从左到右，从下到上为每个栅格编号，每个坐标（xi，yi）对应一个编号N。

在初始种群生成时，对当前栅格，有8 种可选择的方向，当栅格位于四顶角或者边界时，可选择的栅格分别为3 个和5 个。根据当前点和目标点的位置关系，对可供选择的栅格，以概率随机选择一个自由栅格作为下个路径点，以此直到到达路径终点。用这种方式产生的初始种群保持了有效性，连续性和多样性，而且避免了路径反复出现和原地转圈。

3.2.2 选择算子

NSGA-II 算法的选择算子采用精英策略，能很好地保持种群的多样性，但存在如文献[8]所证明的缺陷。当有三个优化目标时，若第三个目标函数不是绝对重要，将其中两个目标作为优化函数，第三个目标作为辅助选择算子，所得到的优化结果更能保持种群的多样性，比三个目标所得到的Pareto 前沿分布更优[8]。建立的第二个目标函数能耗最小可间接反映路径的起伏，所以路径起伏的优化不是绝对重要的，对NSGA-II 选择策略进行了一定的修改：对于在选择算子中比较的两条路径的优先级时，先检查相同级别的路径对应的高度值f3，其次再比较拥挤距离值。这样得到的路径既能保持路径最短，又能减少爬坡起伏及控制爬坡高度。具体选择关键过程为：

（1）种群Rt进行非支配排序，求解出一系列非支配集Zi，计算个体拥挤度及适应度f3；

（2）经过非支配排序后的非支配集Z1所包含的个体是整个Rt中最好的个体，将Z1放到新的父代种群Pt+1中；

（3）判断种群Pt+1的规模是否小于N，若是，则继续向Pt+1中添加下一级的非支配集Z2，直到添加到非支配集Zn时，种群规模超出N，则对Zn中每个个体比较f3，使f3值小的优先选择，如果f3相等，再对Zn中每个个体比较拥挤度距离，使拥挤度距离高的种群获胜，取前｛num（Zn）-（num（Pt+1）-N）｝个个体，使种群Pt+1规模达到N。

3.2.3 交叉、变异、删除算子

选择一点交叉方法，随机选择一个交叉点，交换掉两个父代交叉点之后的路径结点，产生新的子代。

在移动机器人的路径规划中，产生的路径均为连续路径，出于防止高变异概率造成个体优越性破坏和种群退化的目的，选择很小的突变概率进行扰动，取pm=0.01。变异的过程为：随机选择一个变异位置，随机产生一个无障碍栅格的编号，代替原来位置的编号。

删除算子的作用是用来判断所产生的路径是否有环路，如果路径产生的序号有重复的点，则删除两个重复点之间的所有路径段及一个重复点。

3.2.4 修正算子

在NSGA-II 算法的基础上，提出对路径中对角，水平，垂直方向的修正算子，考虑生成的路径产生如图2 圈黑的非环路冗余，为了避免机器人绕路和能量的消耗，可用箭头所指的两个对角路径点来代替。现仅对对角修正算子作出说明。

图2 对角冗余的修正算子示例Fig.2 An Example of a Modified Operator for Diagonal Redundancy

（1）路径中随机选择一个状态点pi；

（2）将pi的所有斜对角点记为Dpi；

（3）遍历路径中的点S；

（4）若S 在Dpi中，则移除S 和pii中所有的路径点。

整个进化过程，如图3 所示。

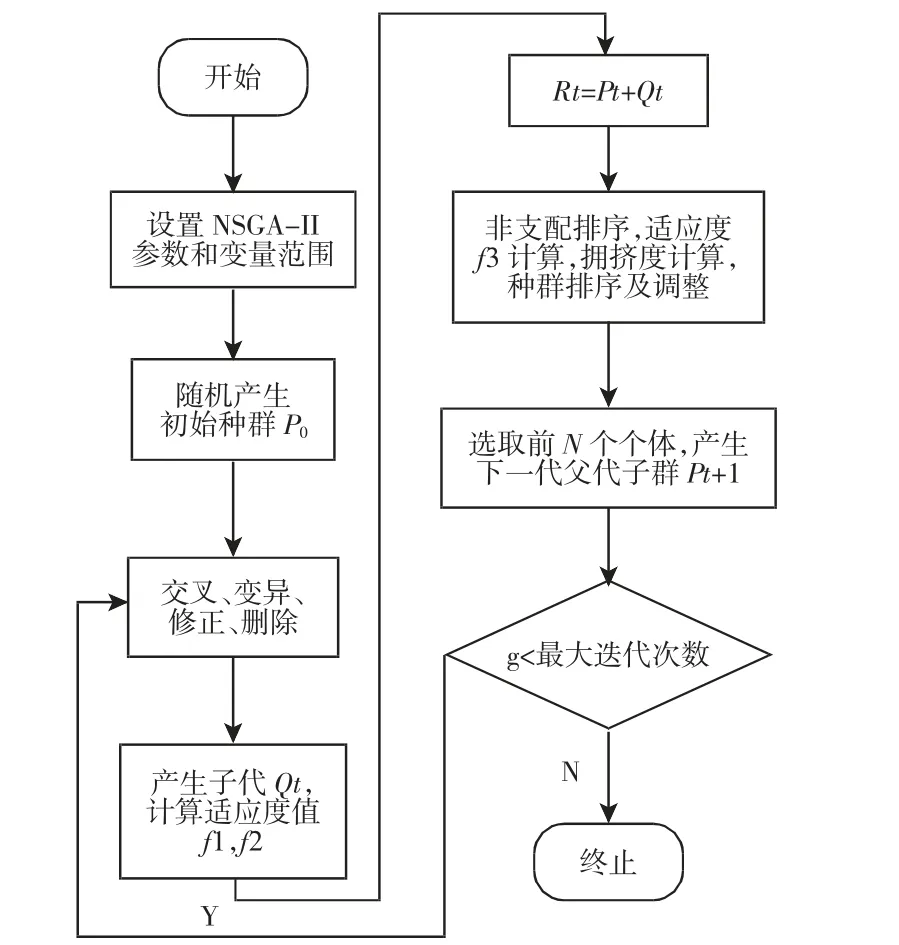
图3 算法流程图Fig.3 The Flowchart of Algorithm

4 仿真分析

采用MATLAB 对上述算法进行仿真测试，实验分别在栅格（10×10）规格，（20×20）规格环境测试，各个参数设定，如表1 所示。

表1 参数设置Tab.1 Preferences

4.1 修正算子有效性验证

实验在10×10 规格栅格环境下，忽略高度信息，只考虑路径最短，建立二维路径规划问题来验证修正算子的有效性，参数设置如表1 中10×10 规格环境。两种算法最优路径的收敛曲线对比，如图4（a）所示。图4（b）为两种算法寻得的最优路径结果，不加入修正算子时在进化第27 代达到收敛，而加入修正算子使算法在进化第10 代达到了收敛，相比之下修正算子使迭代次数减少了约63%，加入修正算子能明显提高算法的收敛性，验证了修正算子的有效性。

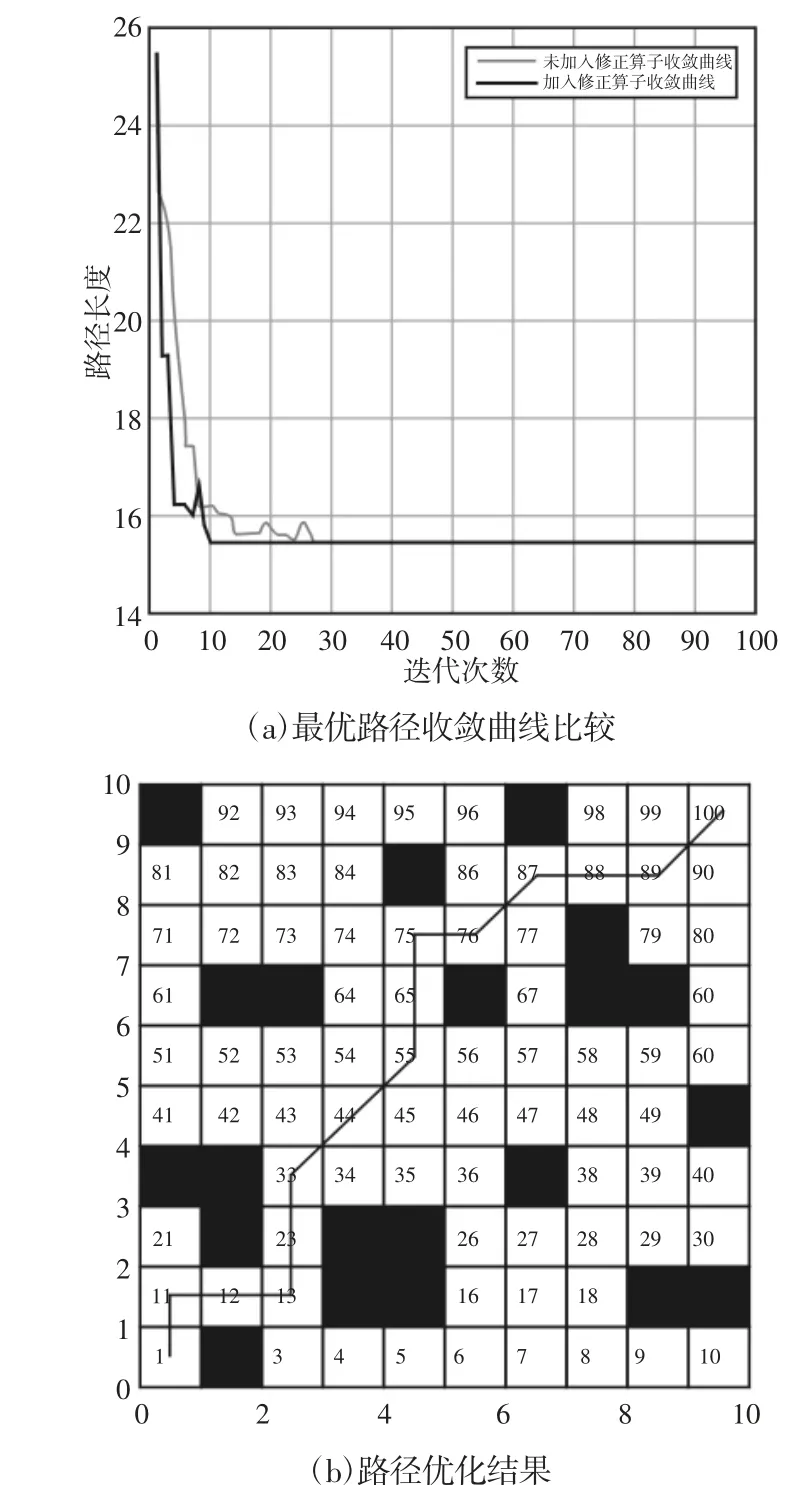
图4 修正算子验证结果Fig.4 Results of Modify Operator Validation

4.2 10×10 规格地图

加入高度信息，为了验证所提出改进遗传算法的有效性，与文献[9]选择相同的机器人工作环境。用提出的改进的NSGA-II 算法来解决文献[9]所构造的规划问题，参数设置如表1 中10×10 规格环境。改进算法所得到的Pareto 前沿分布集，如图5 所示。可以看出，改进算法具有不同的Pareto 前沿解集。前沿集中的一个路径和文献[9]所得的最优路径结果对比，如图6 所示。两种算法所得到的最优路径信息对比，如表2 所示。两种算法所得到的路径长度值相等时路径所消耗的能量明显低于文献[9]，且得到的前沿路径所有的能耗值均低于文献[9]的最优路径能耗，如图6 所示。可见将多目标加权处理成单目标所得到的结果往往不能Pareto 占优，且无法衡量结果是否最好。通过表2 发现得到的Pareto 前沿路径在权衡能耗最小和路径最短的条件下做出了很好的折中。

图5 Pareto 前沿分布1Fig.5 Pareto Optimal Fronts Distribution 1

图6 路径结果对比Fig.6 Comparison of Routs

表2 两种算法最优解对比Tab.2 Comparison of Optimal Solutions Between Two Algorithms

4.3 20×20 规格地图

在（2）的基础上加大栅格环境和障碍物个数进行仿真测试，参数设置如表1 中20×20 规格环境。结果显示当加大栅格数目时，算法依然能找到Pareto 最优路径，而且具有多个Pareto 前沿分布解，如图7 所示。具有很好的实际应用价值。前沿解集中的其中一个路径结果，如图8 所示。

图7 Pareto 前沿分布2Fig.7 Pareto Optimal Fronts Distribution 2

图8 路径寻优结果Fig.8 Result of Path Optimization

5 结论

针对有障碍的三维空间机器人路径规划问题考虑路径最短，能耗最小，起伏最少，构建了多目标优化函数，提出了一种改进的NSGA-II 算法，对算例进行优化分析，结果表明：（1）修正算子的加入能有效提高最优路径的收敛代数，使迭代次数减少了约63%。（2）多目标加权处理成单目标得到的结果往往不能Pareto 占优，且需要人为不断调整权重，实用性不高。改进的NSGA-II 算法具有多个Pareto 前沿分布解，且分布均匀，比传统算法结果更占优。（3）加大规划空间规模和障碍物时改进的算法依然能找到多个Pareto 最优路径，验证了算法在不同复杂度的环境均具有较好的适应能力。