Halbach 方形阵列吸附机构优化设计

方海峰，陈 锦，范纪华，许侃文

（江苏科技大学机械工程学院，江苏 镇江 212003）

1 引言

目前在石化工业、建筑工业和造船业等行业[1-3]，磁吸附式爬壁机器人作为一种可在恶劣、危险、极限、复杂工况下作业的特种机器人，逐渐引起了大众的重视。永磁吸附具有吸附稳定可靠、负载能力强[4-5]等优点，能够在一定高度和倾角的导磁壁面上进行作业，是众多爬壁机器人理想的吸附方式之一，然而卸载困难、易磨损等缺点，一直是制约爬壁机器人发展的重要因素之一[6]。在文献[7]中，设计了一种基于Halbach 直线型磁吸附装置，利用Halbach 阵列的单侧增强性，通过翻转磁吸附单元，可实现机器人的吸附和卸载两种状态，从一定程度上解决了上述矛盾，文献[8]中提出了一种基于Halbach 环形阵列的磁轮，通过调节磁轮的磁化方向来调节磁力。

上述研究均有一缺陷，即吸附单元只有吸附和卸载两种状态，不能实现实时调节吸附力。设计一种基于Halbach 方形永磁阵列的吸附单元，可通过调节磁吸附单元与铁磁壁面之间的空气间隙来实时改变机器人与壁面之间的吸附力。为进一步研究不同因素对吸附力的影响，采用有限元分析方法进行分析，多岛遗传算法用于优化结构，最后通过搭建实验平台来验证结果的正确性。

2 可调磁力吸附单元结构与理论

2.1 爬壁机器人基本结构

爬壁机器人具有的两个必要功能：移动功能和吸附功能。机器人采用轮式作为移动方式，通过差速实现转向功能，如图1所示。机器人在不同倾角的铁磁壁面上，通过自身陀螺仪的监测，传递信号至控制系统，控制滚珠丝杠伸缩作业，来实时调节磁吸附单元与铁磁壁面的吸附间距，进而获得较优的可靠吸附力。将永磁吸附单元装配于吸附结构中，外面由磁轭包裹，有效固定及保护易碎的永磁单元。

图1 机器人结构示意Fig.1 Schematic Diagram of the Robot Structure

2.2 吸附单元基本结构

磁吸附单元内部结构，如图2（a）所示。通过将不同磁化方向的永磁单元按一定的规律排列成正四边形，且侧面和顶部紧贴磁轭，既能有效的按预定方向导磁，又可以方便磁钢的装配。

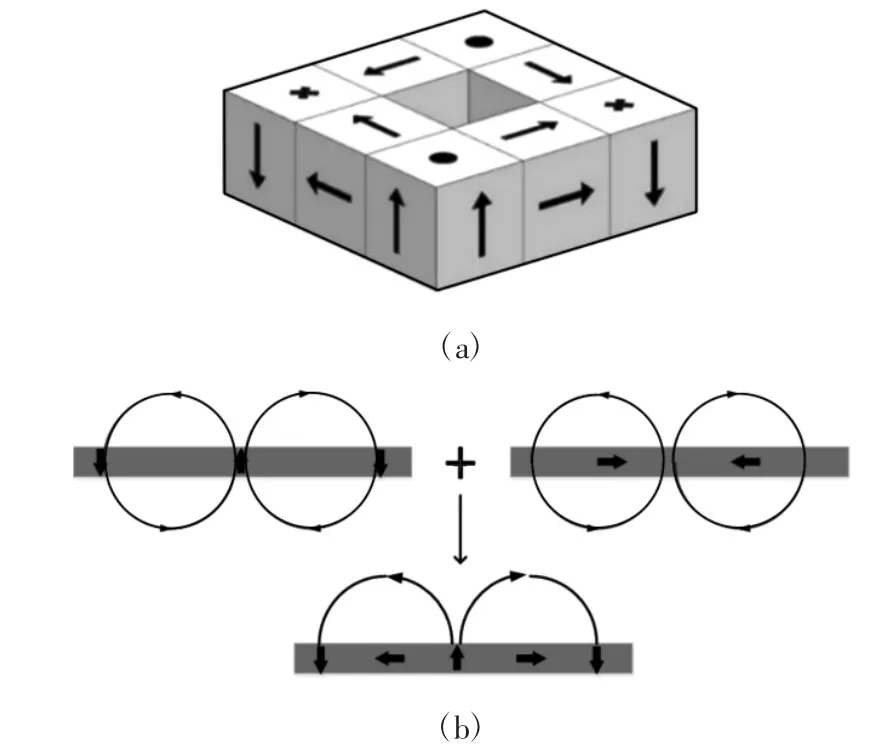
图2 Halbach 磁铁阵列示意图Fig.2 Schematic Diagram of Halbach Magnet Array

Halbach 阵列即指将不同磁化方向的永磁单元按一定顺序排列，形成的阵列磁场具有明显的单侧增强性，如图2（b）所示。此特性可以明显提高磁吸附单元的聚磁效应。

所描述的Halbach 方形阵列基于充磁角度90°磁单元拼接而成，每一边均可形成Halbach 阵列，使得聚磁效应明显。

3 吸附单元影响因素

3.1 吸附单元特性研究

式中：Se—单个网格的面积；

Be—单个网格的磁通量密度；

μ—相对磁导率。

除了本身磁钢的材质上和几何尺寸外，影响磁吸附力的其它因素还有磁向单元的排列方式，磁轭的厚度等。

采用钕铁硼N35 作为永磁材料，其性能参数，如表1 所示。

采用Q235 作为软磁材料，具有低成本，相对磁导率高等优点。将磁吸附力与磁吸附单元体积的比值定义为吸附力体积比λ，即：

式中：Fm—空气间隙下的磁吸附力；n—磁铁拼接个数；V—单个磁吸附单元的体积。

表1 N35 性能参数表Tab.1 N35 Performance Parameter Table

为了比较Halbach 阵列的聚磁效应，根据图2（a）的结构组合，使用传统的对向磁化方式[9]作为比较，为了便于分析，下文均采用磁铁长宽高为20mm*20mm*20mm，铁磁壁面厚度10mm 作为对象，通过有限元方法分析，得出两者的吸附力体积比。

Halbach 阵列单元的吸附力体积比λ 在不同的空气间隙d下，约为传统对向阵列的1.3 倍，即Halbach 阵列单元的永磁利用率优于传统对向充磁单元，如图3 所示。

图3 Halbach 阵列和传统对向的磁吸附性能对比Fig.3 Comparison of Magnetic Adsorption Performance between Halbach Array and Conventional Alignment

3.2 阵列周期之间的影响

定义图2（b）为一个阵列周期，为研究不同阵列周期对磁吸附单元的影响，建立有限元模型进行分析，结果如图4 所示。

图4 不同阵列周期的磁吸附性能对比Fig.4 Comparison of Magnetic Adsorption Performance of Different Array Periods

偶数阵列周期磁吸附性能优于奇数阵列周期，原因在于奇数阵列周期在磁吸附单元的正向和侧向接触处的磁向并没有形成Halbach 阵列磁向，所以体现出来的磁吸附性能略差于形成Halbach 阵列磁向的偶数阵列周期。图4 中2 阵列周期、4 阵列周期和6 阵列周期的比值λ 几乎一致，出于对磁吸附单元结构紧凑以及后期装配的难易度的考虑，选用具有2 个阵列周期的磁吸附单元的结构作为研究对象。

3.3 磁铁尺寸对吸附力的影响

在空气间隙为1mm，其他尺寸条件不变，通过有限元法对磁铁进行分析，结果如图5 所示。随着单块磁铁长和宽的增加，磁吸附力也大大增加，并且存在加速的趋势，且磁吸附力与磁吸附单元体积比λ 随着磁铁长宽的增加先增大后降低；随着磁铁高度的增加，尽管磁吸附力有增加趋势，但趋势趋于平缓，且比值λ 一直处于下降趋势，这是因为前者在磁铁长宽的增加上，其磁通量密度和吸附面积都在增加，而后者只在吸附面积上有增加，也验证了式（7）的正确性。

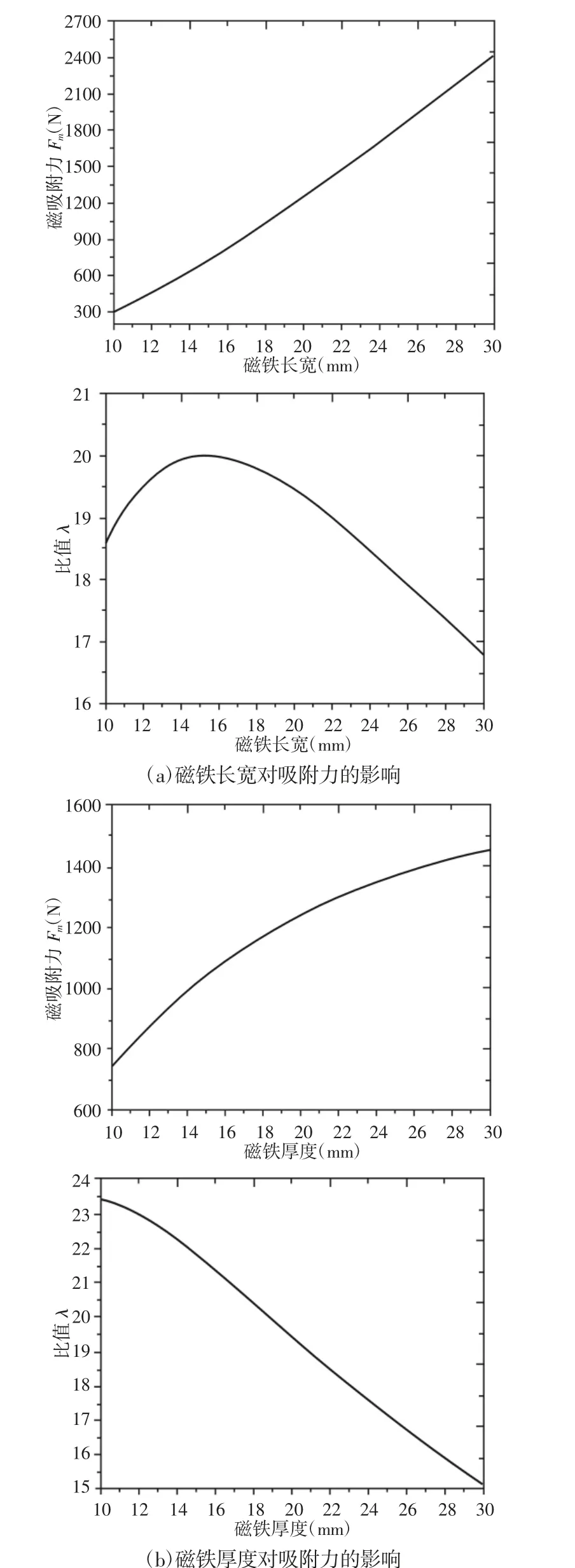
图5 磁铁尺寸对磁吸附力的影响Fig.5 Effect of Magnet Size on Magnetic Attraction

3.4 磁轭厚度对吸附力的影响

磁轭主要作用有减少漏磁现象，达到更好的聚磁效应，以及方便磁铁的装配。磁吸附单元的磁轭分为顶部磁轭和侧面磁轭。而不同结构的磁轭和厚度对磁吸附性能有一定影响。通过有限元方法，分析了顶部磁轭厚度和侧面磁轭厚度对最大吸附力的影响。

最大磁吸附力在（0～15）mm 之间波动，在（3～5）mm，由于厚度过小，顶部磁轭趋于磁饱和增加了漏磁，从而达到最低点，在2mm 附近有效的减少了漏磁现象，并达到最高点，随后增加的磁轭厚度并未能增加最大吸附力，趋于稳定，如图6 所示。侧面磁轭厚度的增加，最大磁吸附力趋于稳定，原因在于，端部磁轭厚度的增加，主要增加的是磁吸附单元的体积，且吸附力没有显著改善，如图7 所示。

图6 顶部磁轭对磁吸附力的影响Fig.6 Effect of Top Yoke on Magnetic Attraction

图7 侧面磁轭对磁吸附力的影响Fig.7 Effect of the Side Yoke on the Magnetic Attraction Force

4 吸附单元尺寸优化及磁力控制研究

4.1 几何尺寸优化分析

4.1.1 目标函数与优化参数

上文分析磁钢长宽相等，侧面磁轭宽度取6mm，阵列周期取2，根据分析，机器人最小许用磁吸附力随着倾角变化范围为（120～498.3）N，为防止铁磁壁面的平整性以及表面铁屑等因素影响，引入影响因子α=1.5，则优化问题表达为：

4.1.2 优化过程与结果分析

磁吸附单元的优化是一个非线性优化问题，全局最优解可以在几个局部最优解中找到。对比解决非线性优化问题的几个常用算法下，采用多岛遗传算法[10]，即模拟生物体在多岛屿环境下的繁衍过程，通过生命体的演化交叉、变异下，寻找种群中的最优解，初始设子种群规模为10，子种群的个数为10，繁衍代数为10，循环迭代为1000，结果如表2 所示。

表2 几组局部最优值对比Tab.2 Comparison of Several Groups of Local Optimum Values

以上为几组极值解，每一小块磁铁的长度a 和宽度b 与吸附力大小呈正相关趋势，如表2 所示。然而，磁铁的过厚会对爬壁机器人的运动灵活性产生负面的影响，磁吸附力和磁吸附单元体积比λ 在当磁铁长宽为22.0mm，高度为5mm，且顶部磁轭为4.9mm 时达到最优值，如表3 所示。优化后的λ 值约优化前的2 倍。

表3 几何尺寸优化前后对比Tab.3 Comparison of the Geometry Optimization Between Before and After

4.2 磁力控制研究

为了评估磁吸附单元的吸附性能并验证结构模型的正确性，本实验采用万能拉压试验机，通过上下两端固定试验对象，来测试磁吸附力和铁磁壁面距离的关系。

4.2.1 实验样机搭建

磁吸附单元采用上文所述的磁向阵列，通过专用夹具的固定和充磁机的整体充磁制作完成，如图8（a）所示。为了消除实验干扰因素，执行以下处理以确保结果的准确性：（1）对铁磁壁面作光滑清洗处理；（2）拉压试验机（图8（b））为铝制合金，导磁率和空气接近一致，且其试验力示值相对误差±0.5%，位移测量分辨力为0.001mm；（3）通过有机玻璃控制磁吸附单元和铁磁壁面的初始距离。

图8 实验搭建示意Fig.8 Schematic Diagram of Experiment Construction

4.2.2 测试值与仿真值对比

通过实验的测试，磁吸附力的有限元仿真值和实验实测值的对比，如表4 所示。

表4 仿真值与测试值对比Tab.4 Comparison of Simulated Values and Test Values

实验结果表明实测值与计算值趋势相同并且数值相近，具有较好的一致性，说明这里对吸附单元有限元优化结果的正确性，其中实测值与计算值存在一定的偏差，主要原因为实际模型尺寸受加工精度的影响，且磁钢拼接处存在一定的间隙。

4.3 可调磁力控制分析

通过控制吸附单元与铁磁壁面之间的间隙来实现磁力的调节，控制流程，如图9 所示。实时调节的难点在于，在已知爬壁机器人在不同倾角下能够可靠吸附的最小吸附力的情况下，如何精确把握空气间隙与磁力之间的关系。

图9 控制流程图Fig.9 Control Flow Diagram

由实验测试，磁吸附力表现，如图10 所示。

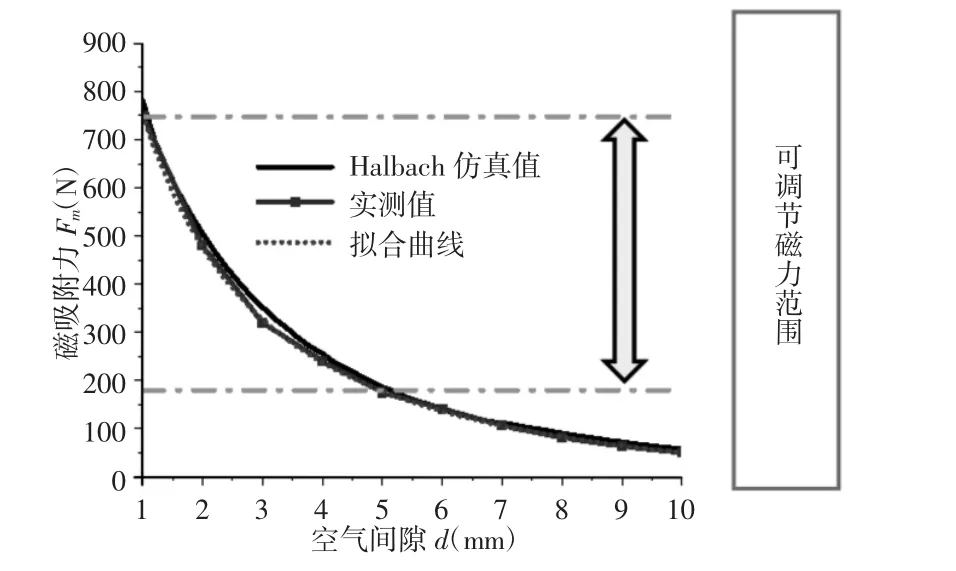
图10 可调磁力范围示意图Fig.10 Schematic Diagram of the Adjustable Magnetic Range

机器人作业时，可调空气间隙范围（1～5.2）mm。通过对实测值曲线拟合，得到吸附力与空气间隙的变化关系，有如下函数表述：

式（10）可为计算空气间隙d 提供数学依据，其拟合度R2因子为0.9962，满足调节吸附力的精度要求。

5 总结

（1）设计一种基于Halbach 方形阵列的磁吸附单元，其永磁利用率优于传统对向充磁单元；采用有限元方法对吸附单元结构进行仿真分析，得到了尺寸因素对磁吸附力的影响。运用多岛遗传算法对其结构进行优化，在满足吸附要求的基础上，优化后的吸附力体积比λ 较优化前提高了近100%。（2）利用万能试验机对吸附机构进行测试，测试结果与仿真值趋势相同且数值相近，表明了分析的正确性；对实测值进行曲线拟合，得出空气间隙与磁力之间的函数关系，为爬壁机器人可变磁力控制系统的设计提供理论依据。