力学性能对闸剪剪切精度的影响分析

王 勇，朱世凡，王 奇，于 珺

（1.合肥工业大学机械工程学院，安徽 合肥 230009；2.马鞍山市中亚机床制造有限公司，安徽 马鞍山 243131）

1 引言

与摆式剪板机相比，闸剪从结构上避免了游隙的存在并可调节剪切角，具有更高的效率、精度和可靠性。但闸剪在剪切宽厚板或高强度薄板时，仍存在机床变形影响剪切精度等问题，需要在设计中进一步分析其力学问题。

目前闸剪多通过组控制系统设计与自动化改造[1]、刀具间隙调节系统的设计[2]与液压系统性能分析[3]等，加强对机床构件的相对控制精度和液压系统的优化，提高闸剪的剪切精度，但缺乏对机床自身构件影响剪切精度的分析；同时研究了闸剪剪切力的变化[4]及以点受力模拟剪切过程的有限元分析[5]，但分析时仅仅作为刚度性能的验证，缺乏进一步分析力学性能对剪切精度的影响。现有文献在闸剪刚柔耦合动力学及力学性能对误差影响的研究分析尚少见。基于此，对比分析了闸剪在刚体与刚柔耦合两种模型下的动态特性，结合静力学分析验证剪板机刚度性能及得出机床主要构件变形对剪切精度的影响，并通过多体系统理论分析得出误差源进行验证，同时为提高闸剪剪切精度提供理论基础。

2 刚体动力学分析

对6×3200 型数控闸剪进行研究分析，其结构数模，如图1所示。工作时，伺服电机通过滚珠丝杠驱动后挡料装置调节剪切长度，压料油缸将被剪板料压紧，设置刀刃间隙和剪切角等剪切参数后，两端的液压缸驱动上下刀刃相对运动完成板料的剪切。

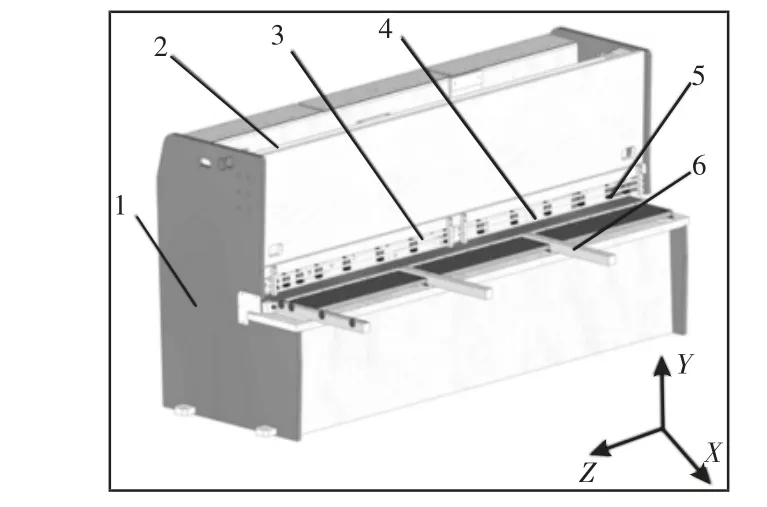
图1 闸式剪板机结构数模Fig.1 Structural Model of Braking-Type Plate Shearing Machine

对闸剪进行动力学仿真，具体分析步骤，如图2 所示。

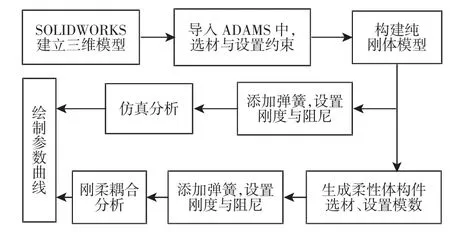
图2 动力学分析步骤Fig.2 Dynamic Analysis Steps

2.1 刚体模型构建

建立闸剪三维模型并进行简化，保存为Parasolid（.x_t）格式后导入ADAMS/View 中，通过布尔操作合并相关构件，将剪板机简化成由机架、上刀架、刀刃、液压缸等主要构件组成的刚体模型。

2.2 参数设置

设置各构件材料属性及约束，具体如表1 所示。

表1 剪板机构件材料及约束Tab.1 Material and Constraints of Plate Shearing Machine Mechanisms

根据液压缸行程，将剪切油缸驱动函数设置为STEP5（time，0，0，4，250）+STEP5（time，4，0，6，-250）；并选Y 负方向为重力方向，大小为默认值。得到刚体虚拟样机模型，如图3 所示。

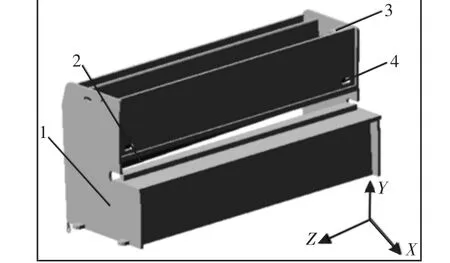
图3 剪板机刚体虚拟样机Fig.3 Rigid Body Virtual Prototype of Plate Shearing Machine

分析过程以弹簧模拟板材[6]，测量不同剪切位置各构件受力变化。为简化测量，在上刀刃剪切起点至终点等距建立5 个节点。以剪切6mm 普通钢板为例，在每个节点添加弹簧。

剪切力主要由两部分组成[7]：两构件的相互切入而产生的弹性力；相对速度产生的阻尼力。刚度系数和阻尼系数根据工程经验[8]分别按K=1.0×108N/m、C=50kN·s/m 取值。

2.3 仿真结果分析

剪板机工作周期为9～13 次/min，设置仿真时间为6s、步数为720，得到机床工作时各节点作用力变化曲线，如图4、图5 所示。

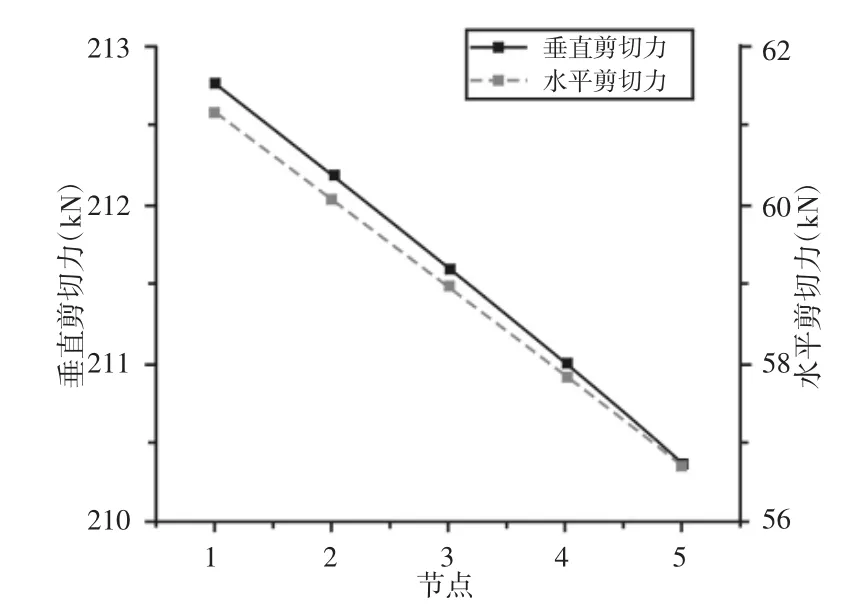
图4 剪切分力大小变化Fig.4 Variation of Shear Force Component

由图4、图5 可知，机床剪切过程中，垂直剪切力变化较小，与诺沙里公式[4]计算值213.8kN 相近；水平剪切力变化较为明显，与计算值63.8kN 相差较大；液压缸受力变化较为明显，且剪切开始时有冲击作用。

图5 液压缸受力变化Fig.5 Force Variation of Hydraulic Cylinder

分析得到了机床工作时，刚体模型下各构件受力值及变化规律，即剪切力与液压缸推力均有减小趋势，但变化范围较小。

3 刚柔耦合动力学分析

剪板机在实际工作中，部分构件在外力和惯性力的作用下将发生弹性变形，为更准确分析剪板机受力变化，建立刚柔耦合机床模型研究其动态特性。由上节分析可知，机床剪切过程中构件受力变化较小，故本节只对比分析刚性模型与刚柔耦合模型下最大作用力。

3.1 柔性体的建立

闸剪剪切时上刀刃运动速度及板材对其作用力较大，用柔性体替换其刚性体，构建刚柔耦合模型。

直接利用ADAMS/ViewFlex 模块生成上刀刃柔性体MNF文件[9]，上刀刃转换柔性体时材料选择5CrMnMo，模数设置为10。生成柔性体后，原刚体构件被替换成为失效状态，但保留了其约束及节点信息，需在节点处重新添加弹簧。

3.2 仿真分析

设置仿真时间为6s、步数为720。仿真时上刀刃变形较大，需在上刀刃与上刀架之间添加多个固定副，并定义其有效与失效模拟真实约束关系。通过定义上刀刃两种模型的失效与有效，实现刚体模型与刚柔耦合模型切换仿真[10]。两种模型下，机床主要构件受力变化曲线，如图6～图8 所示。

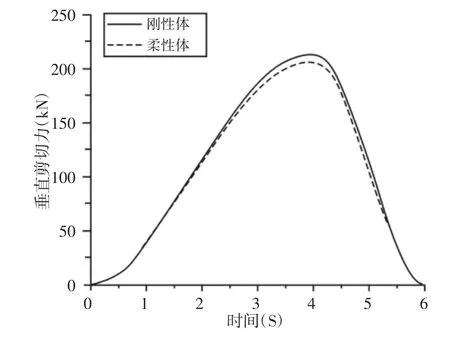
图6 垂直剪切力变化曲线Fig.6 The Changing Curveof Vertical Shear Force

图7 水平剪切力变化曲线Fig.7 The Changing Curve of Horizontal Shear Force

各作用力具体数值，如表2 所示。由图6～图8 和表2 可知，剪切时柔性体上刀刃发生弹性变形，垂直剪切力相比纯刚体稍有减小，水平剪切力稍有增大，但柔性体的剪切力比纯刚体稍小；刚柔耦合模型下，液压缸受上刀架作用力小于纯刚体模型，且起始为拉力（Y 正向）后变为推力。

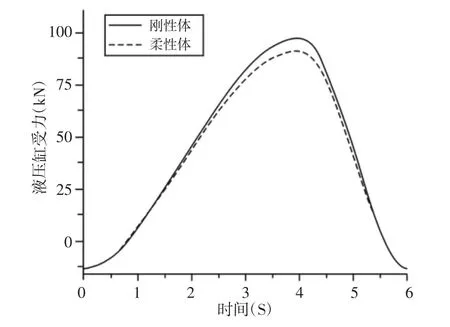
图8 液压缸受力曲线Fig.8 The Force Curve of Hydraulic Cylinder

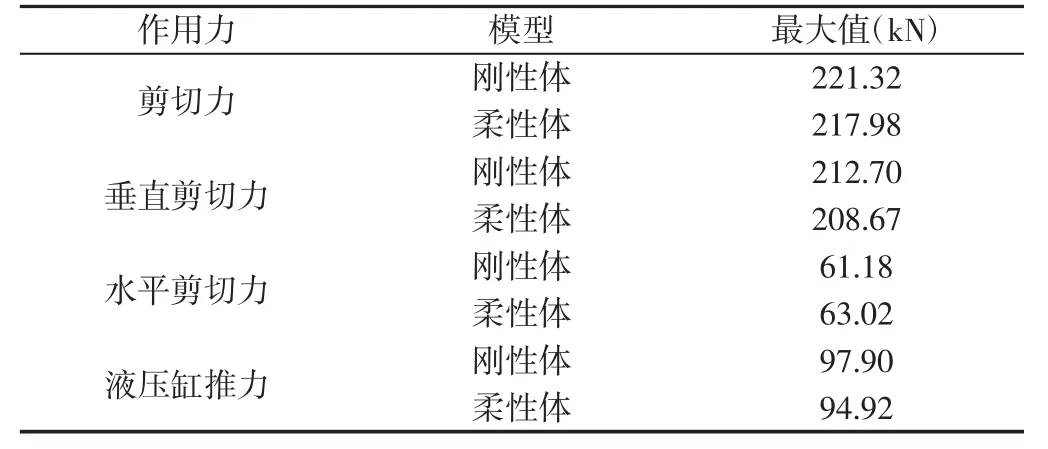
表2 作用力值Tab.2 Force Values

分析得到了机床工作时，两种模型下的各部件受力差异、刚柔耦合模型下各部件受力值及变化趋势。

4 静力学分析

根据表2 中刚柔耦合分析得到的剪切力、液压缸受力等参数值对机床进行静力学分析以验证其刚度性能和得出影响剪切精度的变形位置。分析时，以滑块模拟剪切时刀刃与板材的接触区域，并将剪切力设置为均布载荷作用于其表面。在SOLIDWORKS 中，分别对刀刃节点（1～5）处添加滑块，并忽略过渡圆角、螺纹孔等[11]。仿真分析时，将简化的三维模型导入WORKBENCH 软件中，参考表1设置各构件材料；机架作固定约束，并设置绑定接触模拟剪板机各构件的焊接和螺纹固定，对机床各构件添加作用力。通过静力学分析，得到机床主要部件所受最大等效应力与最大变形。

4.1 上刀架结果分析

通过静力学分析，得到了上刀架在各节点位置最大应力及各向最大变形，具体如表3 所示。

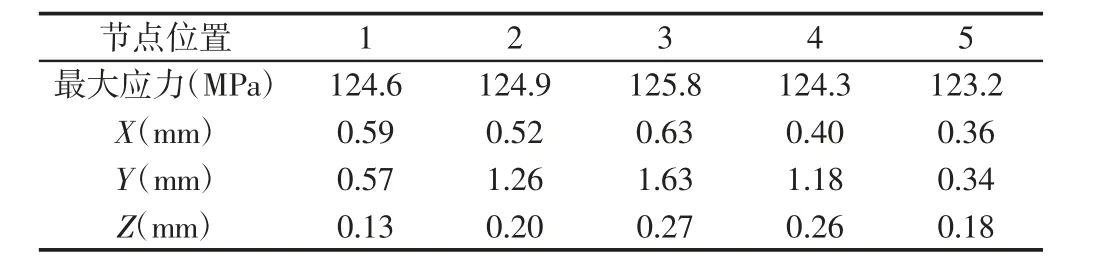
表3 上刀架各节点最大等效应力与各向最大变形Tab.3 Maximum Equivalent Stress and Maximum Deformation of Each Node of Tool Holder

由表3 可知，剪切过程中，上刀架所受等效应力变化较小，在节点3 位置所受等效应力最大；上刀架X、Y 向变形较大，Z 向变形较小且呈现出内凹的趋势。上刀架所受最大等效应力及Y向最大变形，如图9、图10 所示。

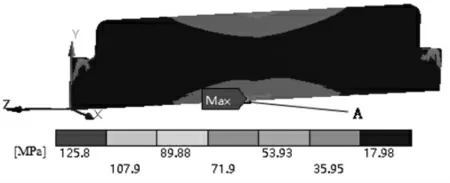
图9 上刀架最大等效应力Fig.9 Maximum Equivalent Stress of Tool Holder

由表3 和图9、图10 可知，节点3 位置，上刀架所受等效应力最大且位于刀片与刀架接触区A 处，大小为125.8MPa，小于上刀架的屈服强度235MPa；上刀架Y 向变形最大且位于后支板B 处，大小为1.63mm，但刀刃处Y 向变形为0.52mm，上刀架和上刀刃均有较大变形，对剪切精度影响较大且在剪切中点时影响最大。

图10 上刀架Y 向最大变形Fig.10 Maximum Deformation in Y Direction of Tool Holder

4.2 机架结果分析

通过静力学分析，得到了机架在各节点位置所受最大应力及各向最大变形，如表4 所示。

表4 机架各节点最大等效应力与最大变形Tab.4 Maximum Equivalent Stress and Maximum Deformation of Each Node of Frame

由表4 可知，剪切过程中，机架在节点1 和5 位置所受等效应力较大，其它节点位置较小，并在节点1 位置值最大；机架X向变形最大，Y、Z 向变形相近且变形范围较小。机架所受最大等效应力及X 向最大变形，如图11、图12 所示。

图11 机架最大等效应力Fig.11 Maximum Equivalent Stress of Frame

由表4 与图11、图12 可知，节点1 位置，机架所受等效应力最大且位于喉口C 处，大小为155.7MPa，小于机架的屈服强度235MPa。节点3 位置，机架X 向变形最大且位于工作台支撑板D处，大小为0.59mm。面板在X、Y 向均有较大变形，墙板Z 向变形较大，同时机架变形将导致其他部件及工件产生移位，增加了变形量，影响工件的剪切精度。

图12 机架X 向最大变形Fig.12 Maximum Deformation in X Direction of Frame

5 闸式剪板机的误差分析

通过以上对闸剪的力学性能分析可知，剪切时上刀架、机架变形较大，将会影响落料的毛刺和尺寸精度，进而降低闸剪的剪切精度。现通过多体系统理论及敏感度计算分析误差源，验证上述分析的准确性。

通过多体系统理论，利用低序体阵列将剪板机的各相邻结构拓扑关系进行描述，同时建立其在广义坐标中的变换关系，得到闸剪的整机误差模型。简化模型时，首先忽略距离分析位置相对较远且不会使受力改变较大的部分[12]；其次考虑部件的相对运动，忽略传递方式的影响，因此将刀具到工件之间的运动传递路径作为拓扑结构链。闸剪的简化结构，如图13 所示。

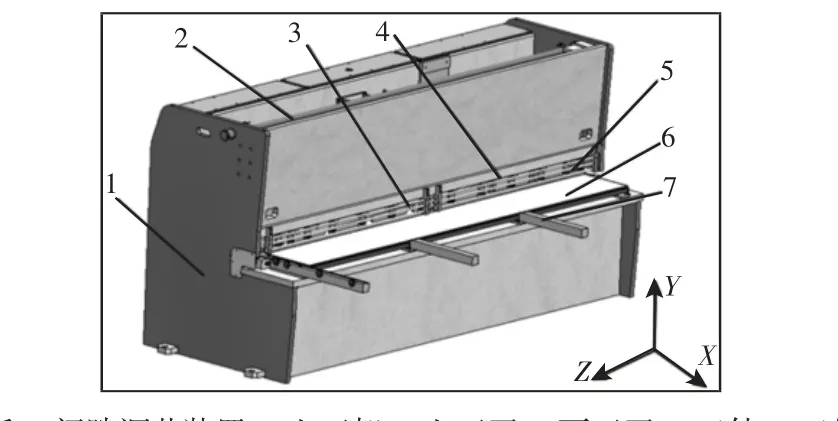
图13 闸式剪板机结构简图Fig.13 Structure of Braking-Type Plate Shearing Machine

闸剪各部件在制造和运动过程中存在位姿误差和运动误差两部分，分析时需考虑相对位置误差、相对位移误差、闸剪几何和运动误差及机床工作时热变形和力变形所引起的误差。

齐次坐标变换公式为：

其中，矩阵表示相邻两低序体之间的坐标变换；闸剪各个部件的位置误差、运动误差相互影响，形成整机误差。在误差模型中，通过对各误差计算得到敏感度系数，得出各部件对整机综合误差的影响程度。

根据计算出的相邻低序体误差特征矩阵和敏感度公式，得到闸剪的敏感度矩阵Si：

式中：△ei—几何误差元素。

所求的总体误差模型简化后有24 项误差，因此敏感度矩阵表达式为：

式中：S4×24—24 项误差的敏感度矩阵；E24×1—24 项误差元素矩阵。

对总体误差模型E 的24 项误差E24×1求偏导数，可以求出每一项误差的敏感度表达式S4×24。根据闸剪实测误差数据，角误差和线误差结果在0.01 左右，因此在以下计算中统一取角误差δ为0.01°、线误差ε 为0.01mm，初始位置L 取1mm。

根据上述公式及数据计算得出误差模型E 在各方向的敏感度系数值Ex、Ey、Ez，如表5 所示。

表5 Ex、Ey、Ez 的敏感度系数值Tab.5 Sensitive Coefficient of Ex、Ey、Ez

对敏感度系数进行分析，得以下结论：

（1）闸剪相对位置误差只存在于间隙调节装置和刀架之间；

（2）闸剪相对运动误差存在于下刀刃和工件、墙板和间隙调节装置、间隙调节装置和刀架之间；

（3）上述刀架、下刀刃均连接与上章所述上刀架，间隙调节装置、墙板均属于上章所述机架部分；分析得出对误差源影响最大部分与闸剪工作过程形变最大部分相一致。

6 结语

以一款6×3200 型闸剪为分析研究对象，通过动力学分析得到了机床在刚体和刚柔耦合模型下剪切时机床主要部件受力变化曲线，并对比分析了仿真结果的差异；其次根据刚柔耦合分析结果对机床进行静力学分析，得出闸剪工作时，上刀架、机架是形变最大、所受等效应力最大的部件；通过多体系统理论及误差敏感度的计算分析，得出了整机最大误差源部件是刀架、间隙调节装置，与力学仿真结果一致，为实际设计、加工提高闸剪精度提供依据。