无人机航拍图像的三维重建方法研究

周祖鹏，张晓东，甘良棋

（桂林电子科技大学机电工程学院，广西 桂林 541000）

1 引言

基于无人机的易控性，以无人机为载体从不同的方位对目标进行航拍获取图像。为图像的重建提供来源。三维重构技术一直是模式识别领域的研究热点和应用热点[1]。传统的重建技术有非接触式三维重建、接触式三维重建、基于图像的三维重建等，其中作为非接触式三维信息采集技术，基于主动结构光建模[2]可以提供一定的点云数据，但是相对较少的点云数量不能完全描述被测目标的所有特性。基于图像的立体视觉方法可以重建出完整的三维模型[3]，但由于图像采集的局限性和成像环境的复杂等因素，三维模型的成像倾向于区域空洞或局部信息丢失。基于光场相机提供的单次拍摄深度估计的功能，虽然可以进行实时的场景三维重建，但是其估算的深度精度仍然有限[4]，所以其重建结果不太理想。

通过控制无人机从不同位置拍摄的图像，搭建图像采集模块保存图像。利用自标定的方法计算相机的内参，然后由不同方向角度拍摄的图像提取图像的特征点。经常使用到的算法有SIFT 及其变型算法，通常情况下，在不加入图像融合的情况下，所拍摄的每幅图像可能受到外界干扰，导致缺少图像部分信息缺失，从而会降低图像信息的利用率。所以在基于这一理论，在重构中加入图像融合这一部分，在实际应用目标下将相关信息最大合并的基础上减少了图像输出的不确定度，增强系统的可靠性。利用空间坐标公式计算出点空间坐标。最后使用OPENGL 显示点云三维模型，经过三角剖分，纹理贴图最终获得目标的三维模型。这种重建技术对于小范围地图重建[5]，三维位置信息获取，安防技术等方面都有很大的作用。主要通过相机自标定技术和特征点匹配算法，结合图像拼接技术，通过三维点云重建[6]技术，恢复室外场景的三维模型。

2 图像采集平台搭建

采用普通的光学摄像头作为无人机的视觉传感器来采集图像。首先搭建无人机图像采集平台，在地面站规划好无人机的飞行路径，当无人机飞到目标处时，对目标环绕飞行。在航拍图像的无线传输中，需要利用地面基站的DJGO 的“航拍信息处理模块”来传输航拍图像，其内部关系，如图1 所示。

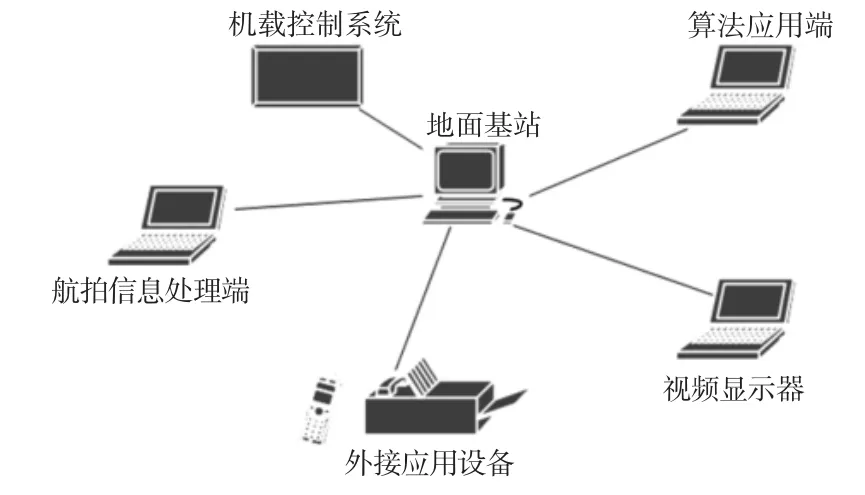
图1 图像航拍系统的内部关系Fig.1 Internal Relationship of the Image Aerial System

利用MFC 搭建图像采集系统，无人机实体模型和可视化窗口，如图2、图3 所示。

图2 四旋翼无人机Fig.2 Quadrotor UAV

图3 无人机图像采集平台Fig.3 Image Acquisition of UAV Platform

3 相机自标定

相机的图像信息可以通过相机参数产生与三维物体有关的几何信息。摄像机标定是一种计算针孔摄像机模型参数的方法[7]。自标定的原理是根据相机模型通过投影变换得到的投影方程，反映出二维图像上的点到三维空间对应的关系，基于Kruppa 方程进行自标定，求得相机内参。通过提高基础矩阵和极点的精度，提高重建的稳定性。其基本原理如下：

4 图像特征提取与匹配

那些具有特殊属性并且具有一些结构意义的图像部分通常被称为图像特征点[8]。这里我们选用SIFT 算子对图像对进行特征点检测与匹配。两幅视图存在通过对极几何一幅图像上的点可以确定另外一幅图像上的一条直线，这里可以用相机基本矩阵F 表示，根据极线约束可知，图像匹配点必须在极线上。在相机1 的像素坐标系与相机2 的像素坐标系的对应点存在如下关系：

将矩阵展开后可得：

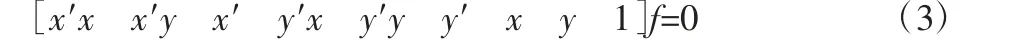
式中：x′和x—两幅图像的任意一对匹配点，每一组匹配点都给出一个F 的线性方程，由于f 的秩是2，则f 的自由度为7，所以至少通过7 组匹配点可以确定F。当n＞7 组匹配点，可以根据最小二乘法确定f。

5 图像拼接与融合

5.1 图像特征点配准

基于SIFT 特征点的提取，描述，通过特征点的匹配，找到两幅图像中匹配点的位置，进一步使用图像中的匹配点得到两幅图像的变换矩阵H。根据对极几何原理可知，对于平面靶标上一点在不同的图像坐标系中的关系如下：

当平面靶标有四个点对或更多的时候，可求解H 矩阵，根据前面计算的H 矩阵，就可以利用变换公式x′=Hx 计算变换以后的坐标x′和在原有的图像中的像素坐标x。

5.2 图像插值

由于在映射过程中，x 的坐标不是整数，所以为了获得对应的像素值，必须要对像素值进行插值，这里我们采用双线性插值法。首先在u 方向上进行两次线性插值，然后在v 方向上进行一阶线性插值。

5.3 最小二乘法求变换矩阵

在建立适当的模型之后，就需要求解H 的参数来获得两幅图像之间的变换关系。

式中：x′和y′—基图像的横坐标和纵坐标，x 和y—要求的图像横纵坐标。将上列式子写成矩阵的形式可以得到如下结果：

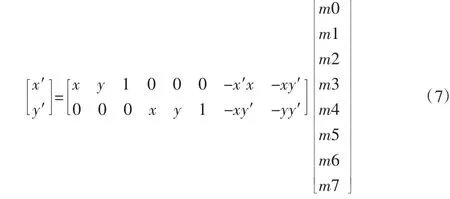
5.4 图像融合

采取基于特征的图像配准方法。基于特征的配准方法对于图像中出现的光照不一致，旋转、仿射等变换等具有很好的鲁棒性[9]。在图像融合过程中，需要对缝合线进行处理。本节采用加权平均法处理拼接缝隙问题。

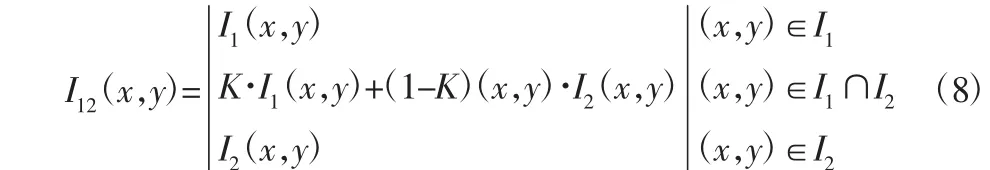
式中：I1（x，y），I2（x，y）—待融合的两幅图像；I12（x，y）—加权融合后的图像。K=d1/（d1+d2），式中d1d2—重合区域的点左边界和右边界的距离。

6 三维重建

通过特征点的匹配以后，紧接着要获取空间三维坐标，假设两幅图像上的一对匹配点m1（u1，v1，1）T和m2（u2，v2，1）T，则由二维图像素点与三维点之间的映射关系可得：

式中：P1，P2—对应图的投影矩阵；M—空间三维坐标；K1，K2—比例系数。将上述得到的三维空间点导入OpenGL 中，用坐标点的绘制方法重建场景的三维图像。

7 实验结果与分析

7.1 实验流程与分析

实验流程图，如图4 所示。在传统的三维重建过程中没有加入图像拼接融合这一部分，将图像拼接融合算法用于图像三维重建中，如图5 所示，以此来能够很好地整合多源图像间的冗余和互补信息，改善了光照不均匀造成的匹配性渐晕现象以及光学中心的不期望运动引起的视觉效应所造成的错误匹配和径向失真。图像融合就是利用冗余性来增强在某一源中不清晰的特性，利用互补性来弥补在某个传感器所缺失的信息。其结果是将多源图像中的信息都综合到融合结果中去，以增强和优化后续的显示和处理过程。

使用像素级图像融合方法中的加权平均法，就是直接对源图像对应像素灰度值进行加权平均融合处理。对于源图像A，B，F为它们的融合结果，其加权平均融合过程如下式：

式中：（i，j）—源图像像素点的位置坐标位置；w1和w2—加权因子。从公式可以看出该方法在一定程度上提高了融合的计算速度。

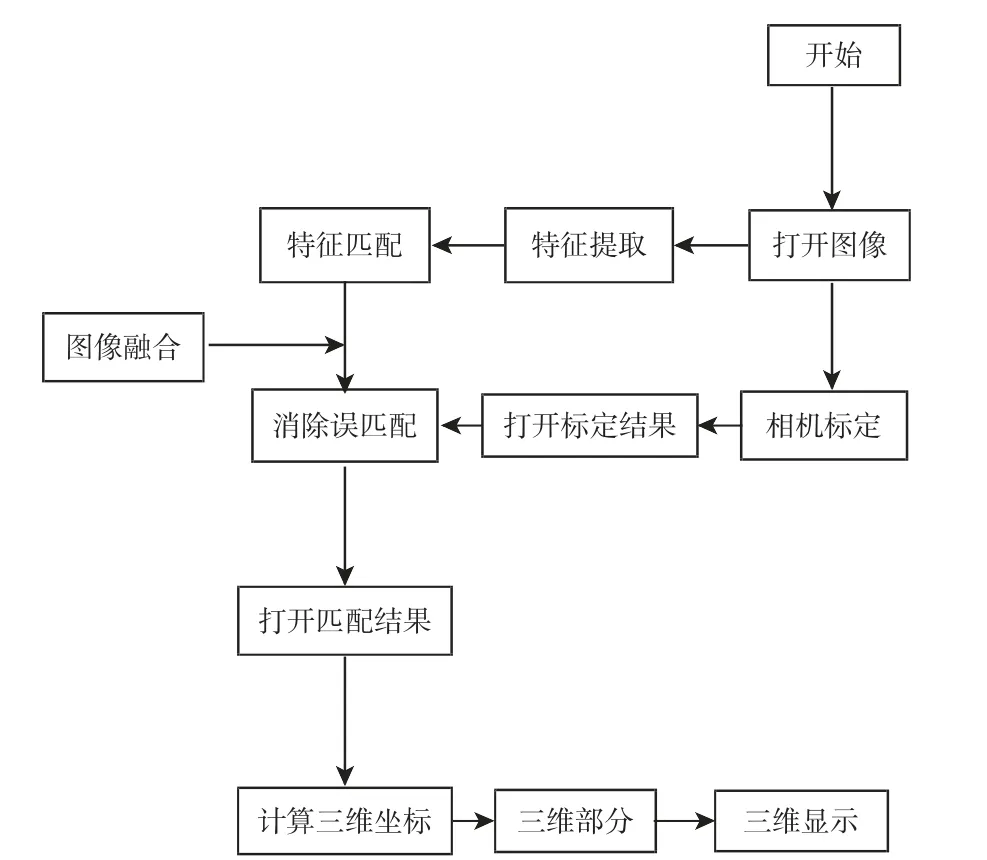
图4 实验流程图Fig.4 Experimental Flow Chart

同时在图像三维重建中加入图像拼接融合将加入图像融合前后的重建结果进行对比，主要观察融合前后特征点检测和匹配点对个数，进一步分析加入图像融合前后的特征匹配率大小，

从以上表1 可以看出，加入图像融合之后，重建的目标信息更加丰富全面，特征点匹配率大大提高。图中建筑物的各个形貌特征在加入图像融合之后，能够较大程度上还原图像特征。

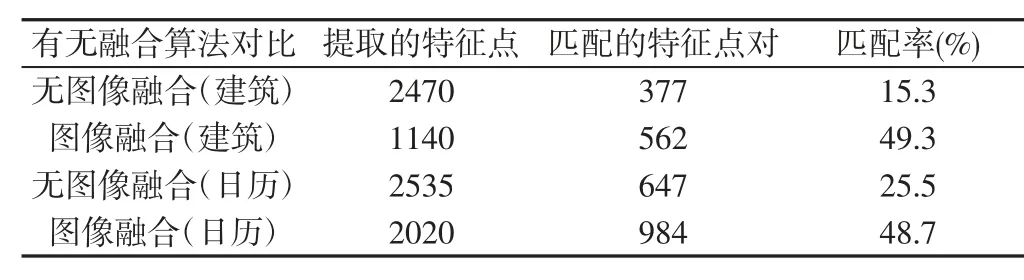
表1 加入图像融合前后的重建结果Tab.1 Adding Reconstruction Results Before and After Image Fusion

7.2 相机自标定

利用相机自标定方法，无人机从不同角度拍摄的室外和室内图片，如图5 所示。实验硬件为无人机和平台电脑，软件平台为Visual Studio 和Opencv。

图5 两组不同角度拍摄的图片Fig.5 Pictures Taken at Two Different Angles

7.3 特征提取与匹配

利用SIFT 算法对这两幅图进行特征点提取，特征点检测到有2470 个，如图6 所示。

图6 特征点提取与匹配Fig.6 Feature Point Extraction and Matching

7.4 图像拼接与融合

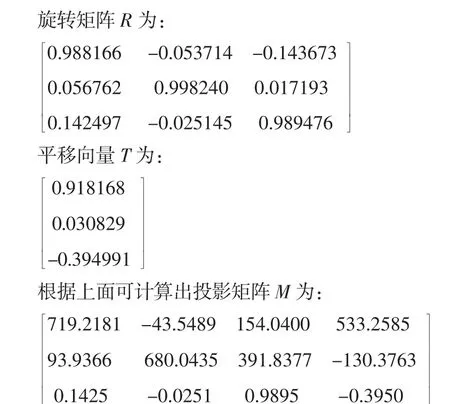
通过SIFT 特征点提取获得上述两幅图的特征点坐标，然后导入Matlab 求取两幅图像之间的变换矩阵H。在这里我选取5对匹配点，通过计算得到H的结果为：

将基于SURF、SIFT 与Opencv 自带的Stitcher 类的拼接三种算法进行对比，从算法的运行时间、效率以及结果综合评估三种算法的融合结果，如图7 所示。从以上的图7 和表2 可以看出，三种不同的方法拼接的结果中，基于SIFT 算法的图像拼接速度更快，及其拼接结果图像显示边缘处理无明显的畸变，融合比较平整。

图7 三种不同拼接方法的实验结果Fig.7 Experimental Results of Three Different Splicing Methods

表2 三种拼接方法的对比Tab.2 Comparison of Three Stitching Methods

7.5 三维重建

将拼接后的图像所得的匹配点空间坐标利用OpenGL 驱动，用三角剖分的的绘制方法重建场景的三维图像，实验结果，如图8、表3 所示。

图8 三种不同方法重建结果Fig.8 Three Different Methods of Reconstruction Results

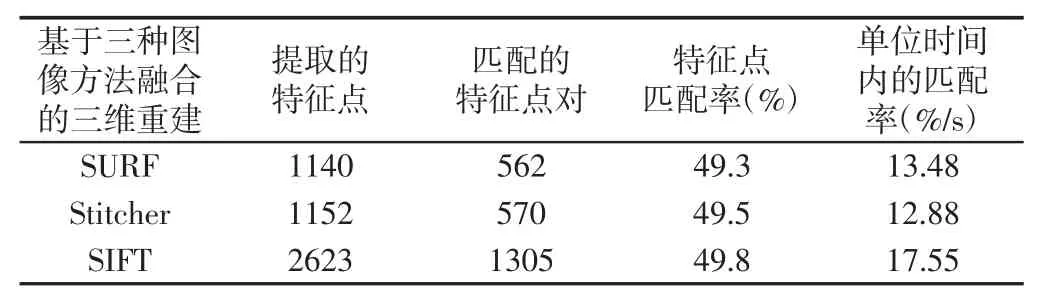
表3 三种不同拼接方法重建效果对比Tab.3 Comparison of Reconstruction Effects of Three Different Stitching Methods

结合以上表图，可以看出基于Stitcher 类融合的三维重建的效果稍差于SURF 类，综合算法运行时间和重建效果，SIFT 类图像融合的重建的单位时间匹配率率高于SURF 类的，其重建的完整度较其他两种算法更好。综合考虑，基于SIFT 类图像融合的进行三维重建有效的提高运行效率。

8 结论

通过无人机为载体，通过无人机的控制航拍同一目标的不同角度的照片，为三维重建提供可靠图像来源。结合图像拼接融合技术和OpenGL 进行目标的三维重建，相比传统的三维重构技术，本方法可有效获取视场多角度的图像信息，能够较为全面的获取接近真实的三维场景模型。此方法一定可满足小范围内室内外环境三维重建。可用于地形地貌勘测和灾区探测[10]等，具有很大的现实意义。当然当图像数量增多时，对算法的稳定性也会要求的更高。如何在更多图像的基础上进行重构以及效率的提高也是今后要研究的方向。