基于全量流动理论的管材弯曲过程失稳分析研究
车移,詹红,屈俊岑,林军
基于全量流动理论的管材弯曲过程失稳分析研究
车移1,詹红2,屈俊岑2,林军2
(1. 中航工业成都飞机工业(集团)有限责任公司,成都 610073; 2. 西南技术工程研究所,重庆 400039)
基于全量流动理论,研究管材弯曲成形过程中的外侧破裂和内侧起皱,分析其产生的原因及控制方法。采用理论解析方法,建立了管材弯曲变形应力、应变计算公式,推导管材外侧破裂和内侧起皱发生的判据,并试验验证了预测公式的可靠性。基于推导的应力、应变计算公式,依据临界许用变形程度,建立了管材外侧破裂判据;采用能量准则,提出了管材弯曲过程起皱发生公式,确定了起皱失稳计算公式的各个边界参数。试验与理论结果表明,构建的最小壁厚下许用/(弯曲半径与管材平均半径的比值)计算公式、基于起皱失稳计算的许用/(弯曲半径与管材平均半径的比值)计算公式均有较高精度,可用于指导弯管工艺参数设计与优化。
管材弯曲;临界变形;能量法;破裂;起皱
弯管类构件与通过转接头连接直管的组合型构件相比,具有质量小、体积小的特点,在航天、航空、航海、汽车、石油化工等领域的装备研制中得到了大量的应用[1]。管材弯曲成形是将直管坯弯成具有一定弯曲半径、一定弯曲角度和形状的塑性变形方法,是弯管类构件制备的关键工序。近年来,随着新一代装备对轻量化的要求越来越高,要求弯管类构件具有壁厚小、直径大、弯曲半径小和尺寸精度高的特点,这也使得弯管成形技术成为先进塑性加工技术的一个重要方向。
管材弯曲成形是一个多因素作用下的塑性变形过程,该过程极有可能产生多种塑性失稳缺陷[2]。在薄壁管弯曲成形工艺中,管材外侧的破裂和内侧的起皱是成形缺陷中最为常见的失稳缺陷,这使得对失稳缺陷的预测和控制成为管材弯曲成形研究中的关键性问题之一。在2000年之前,主要采用设计人员的经验[3]或理论计算方法[4—5]预测管材弯曲过程的壁厚变化和起皱规律并优化工艺;之后,随着计算机技术的迅速发展,数值模拟技术成为了预测管材壁厚变化和起皱规律的主要工具,其模拟精度满足了工艺参数优化的要求[6—11]。然而,采用数值模拟优化管材弯曲成形工艺参数,需要确定初始参数范围,这个范围一般依赖于工艺设计人员的经验或者依赖于理论计算结果。管材弯曲工艺参数的计算方法一般分为两类:一类是基于应力分析的方法[4];二是基于应变分析的方法[5]。已有研究人员指出了这两种方法都有相应的预测缺陷[12—14],尤其是在确定应变分量之间的关系时,一是假设周向应变为0(即平面应变关系),二是设定厚度方向的应变为轴向应变的0.75(三向应变关系),而忽略了分量之间依赖于塑性流动规律的原理。
文中基于塑性流动方法,提出计算管材弯曲过程的应力、应变计算新方法,在此基础上,依据能量准则,提出预测弯曲过程起皱发生公式,研究管材弯曲成形中起皱发生的影响机制,为管材弯曲成形过程的工艺参数的确定和优化创造条件,以提高弯管构件的质量,缩短工艺开发周期,降低成本。
1 管材弯曲成形过程的应力、应变分析
图1为管材弯曲过程的任意一瞬间的剖视图,面为弯曲的对称面,在几何面上的任意一点的应力与几何关系如图1所示,图中:为弯曲半径,为管材平均半径;σ为管材圆周方向的应力;σ为方向的应力。假定径向应力σ=0,那么基于力平衡关系,在面上任意一点的周向应力与轴向(方向)应力的关系可以写为:
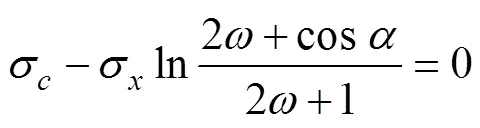
式中:;为无轴向外力作用下的轴向应力;弯曲Px为管材轴向压(拉)力;正负号分别表示拉力和压力;t0为管材厚度;α∈[0,π],在[0,π/2]范围内为管材外侧,在[π/2,π]范围内为管材内侧;令。
假定管材在自由弯曲成形过程未承受轴向压(拉)力,那么图1的截面上任意一点沿方向(一般称为轴向或长度方向)的应变为:
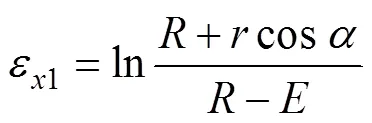
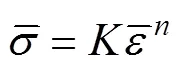
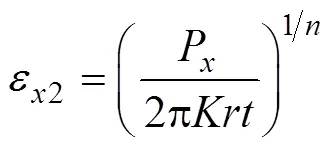
那么管材受轴向压(拉)力作用下,方向的应变为:
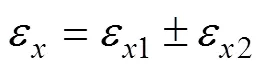
式中:正号代表管材承受轴向拉力;负号代表轴向压力。
2 管材塑性弯曲过程的应力与应变求解
在图1中,基于J2流动理论[15],管材弯曲过程屈服公式可以写为:
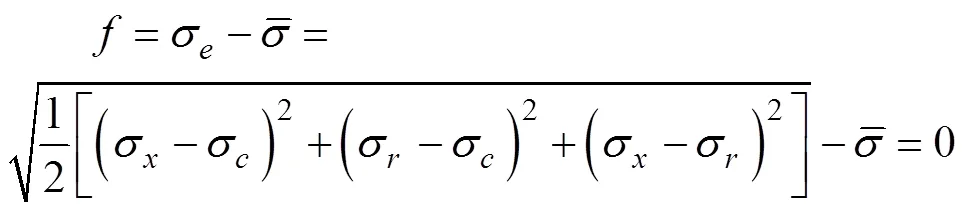
由塑性变形流动理论[15]得知:
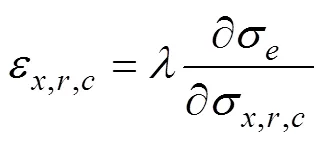
依据式(4)可得:
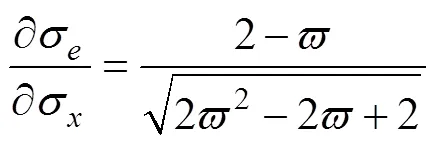
依据式(7)可以得到3个方向应变的比例关系为:
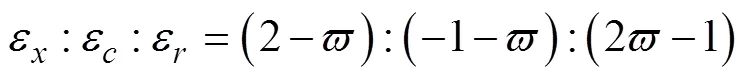
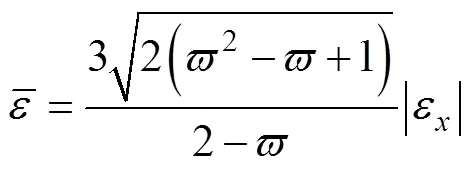
假定管材材料的塑性流动方程满足SWIFT方程,即:
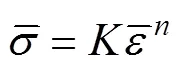
式中:为强化因子,为强化指数。
联立式(5)、(9)、(10),可求解出管材弯曲过程的向应力σ:
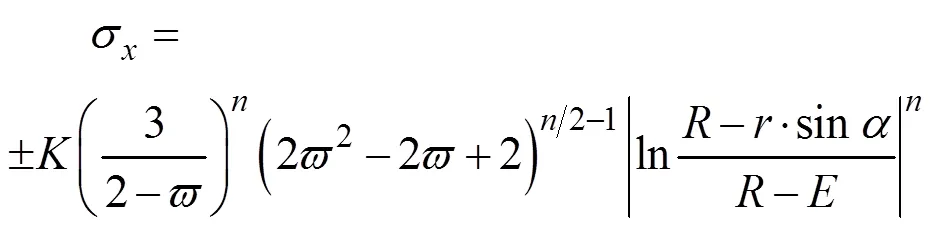
式中:正号为管材中心层外侧;负号为管材中心层内侧。
周向应力σ可以依据式(12)计算:
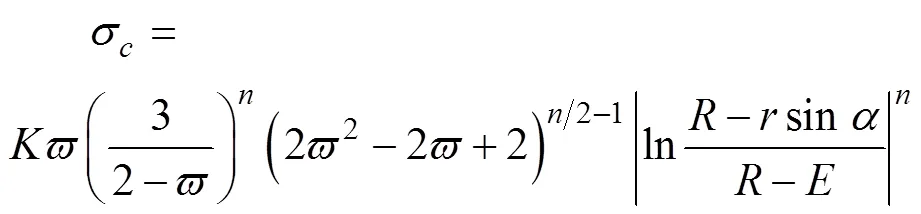
3 弯曲成形的允许变形程度与分析
基于管材弯曲过程的应力与应变计算公式,可以用于计算管材的弯曲成形极限。管材弯曲成形极限包括最外侧的破裂极限和内侧的失稳起皱。如果对弯曲后的管材有壁厚要求,则最外侧的破裂极限可以转为最小壁厚的控制。
3.1 管材弯曲过程的壁厚变化与许用R/r参数
管材依据式(8),可以得到管材弯曲后的径向应变(也为厚向应变)为:
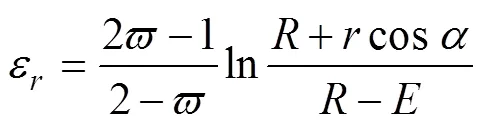
依据式(13)并结合中心层偏移计算公式,可以得出式(13)的另外一个表达式:
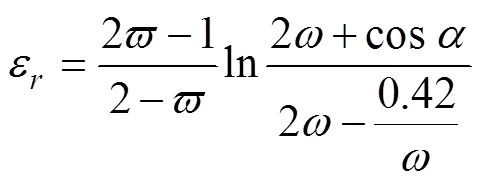
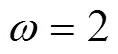
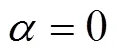
如果要求弯曲后的管材不破裂,那么许用的弯曲极限为:
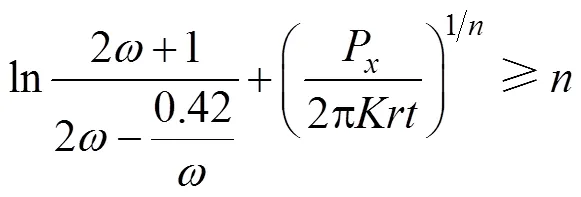
如果最小壁厚要求为min,那么许用的弯曲极限为:
基于式(15—16),采用简单的数值求解方法,即可得最小的/计算区间。
3.2 管材弯曲过程的失稳起皱与许用R/r与r/t参数
在弯曲过程中,管材内侧起皱是弯管工艺的一个主要缺陷。在弯管成形过程中,管材处于塑性稳定状态的条件是外力做功Δ小于材料内部能量Δ。当外力做功增量Δ大于材料内部能量Δ时,管材失稳,即弯曲失稳的判据为:
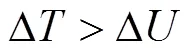
在弯曲过程中,管材起皱区域如图2所示。假定内侧因压缩起皱形成波纹的几何公式为:

依据图2,式(17)的边界条件是:
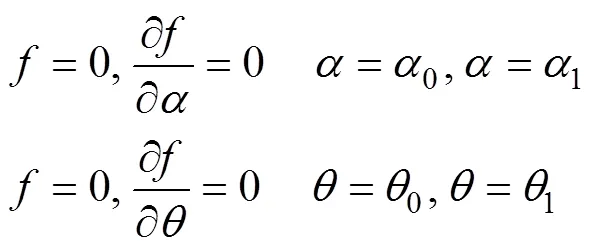
在起皱的瞬间,外力做功增量和内能增量分别为:
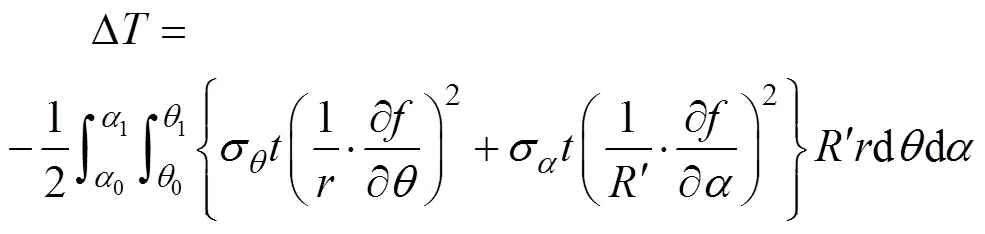
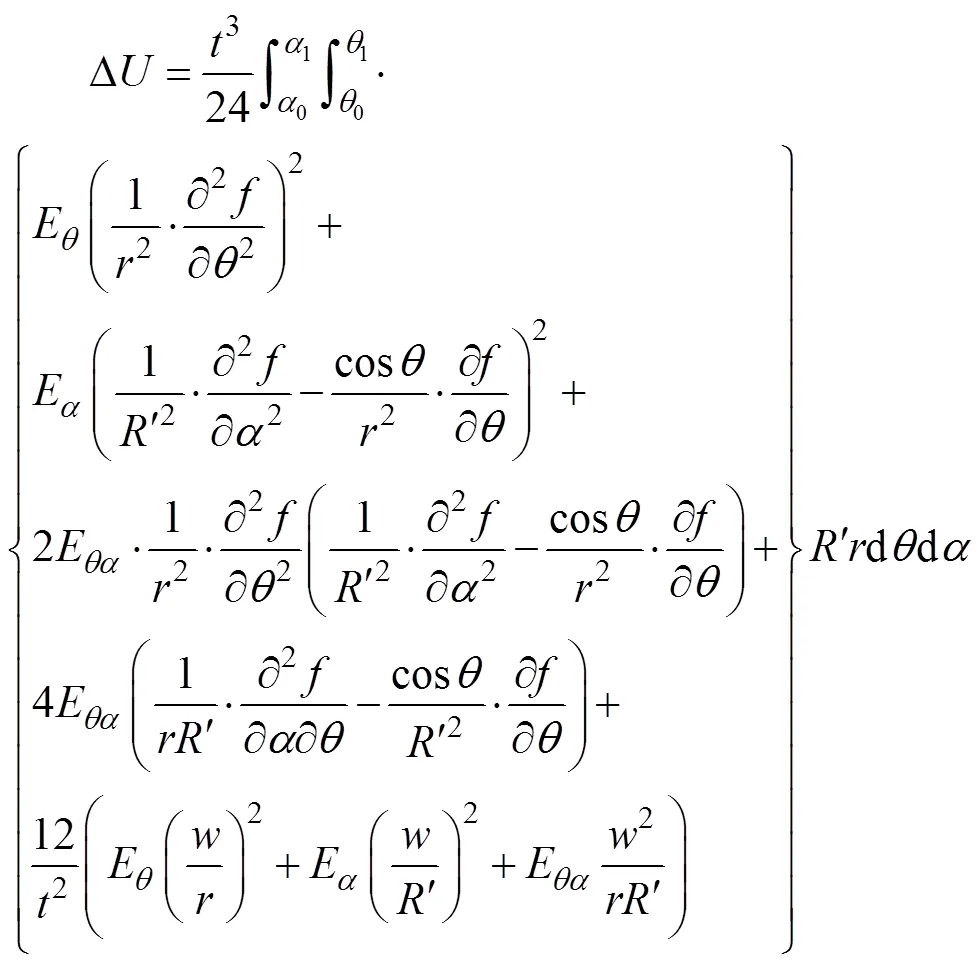
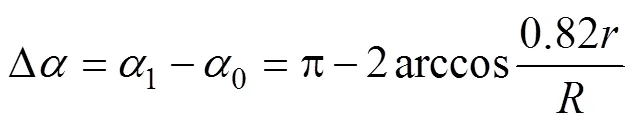
在弯曲过程的某一瞬间,管材起皱区能量总方程为:
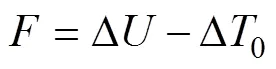
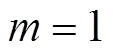

其中:
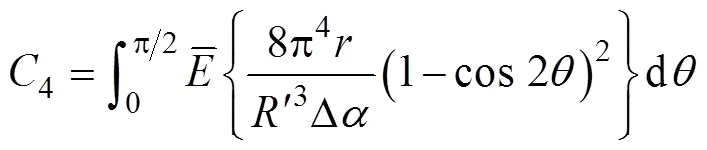
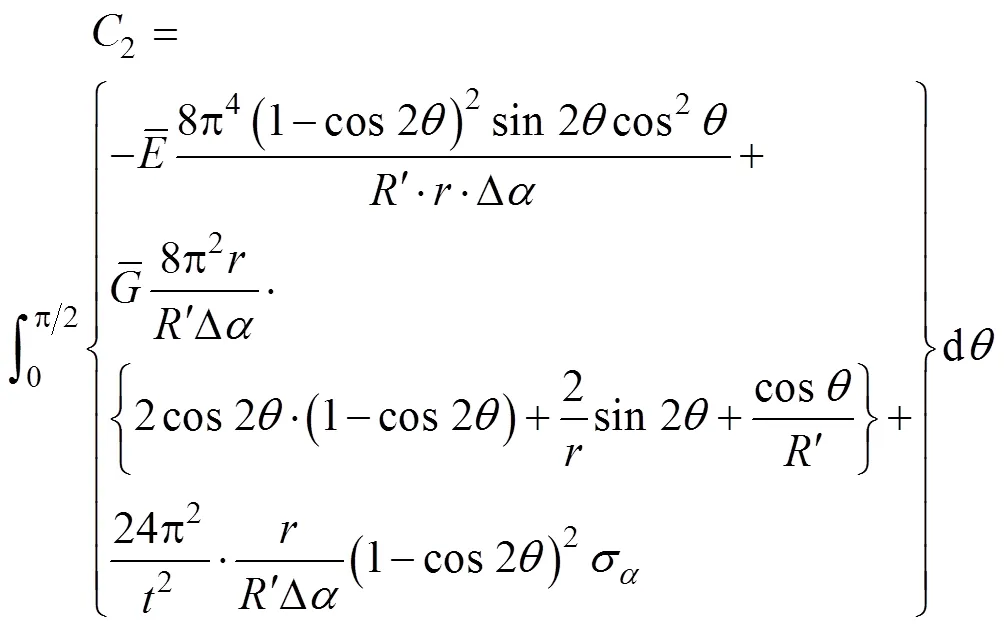
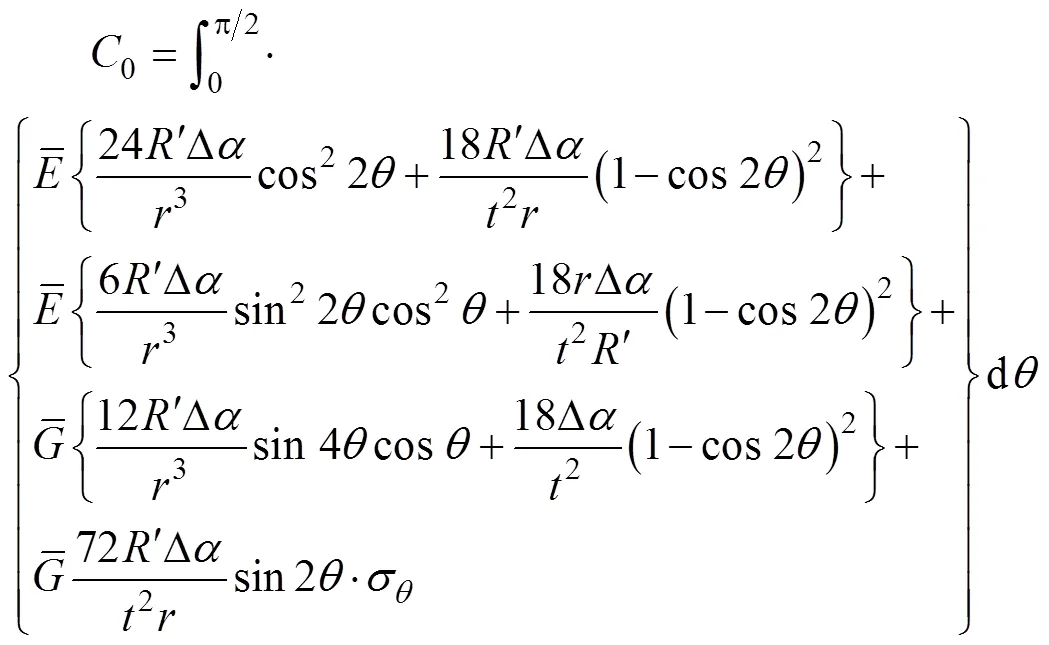
如果图2b的截面起皱区存在,即要求式(24)有实数解,可以得到:
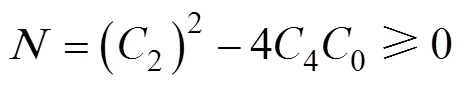
在满足式(28)的条件下,得到临界波数目为:
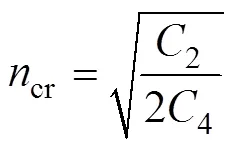
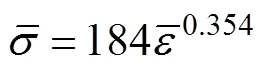
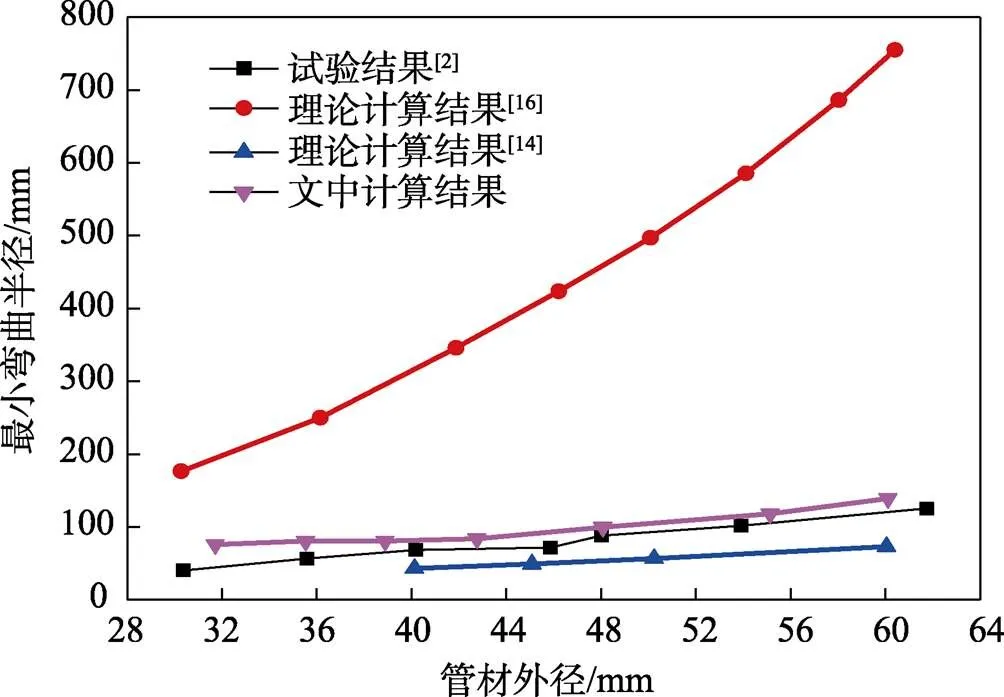
图3 试验与理论计算结果对比
4 结论
1)基于全量塑性流动理论,建立了管材弯曲成形过程的应力、应变计算新公式;进而构建了管材弯曲过程中最小壁厚下的许用/计算公式,同时建立了起皱失稳计算公式,确定了起皱失稳计算公式各个边界参数。
2)试验与理论解析结果表明,构建的最小壁厚下的许用/计算公式、基于起皱失稳计算的许用/计算公式均有较高精度,可为实际工业生产中弯曲成形工艺参数快速优化提供可靠精确的模型。
[1] CHEN Ji-sheng, E Da-xin, ZHANG Jing-wen. Effects of Process Parameters on Wrinkling of Thin-walled Circular Tube under Rotary Draw Bending[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(5/6/7/8): 1505—1516.
[2] 王同海. 管材塑性加工技术[M]. 北京: 机械工业出版社, 1998: 187—192. WANG Tong-hai. Tube Plastic Processing Technology[M]. Beijing: China Machine Press, 1998: 187— 192.
[3] 王孝培. 冲压手册(第2版)[M]. 北京: 机械工业出版社, 2004: 51—55. WANG Xiao-pei. Stamping Manual (2ndEdition)[M]. Beijing: China Machine Press, 2004: 51—55.
[4] STACHOWICZ F. Bending with Upsetting of Copper Tube Elbows[J]. Journal of Materials Processing Technology, 2000, 100: 236—240.
[5] TANG N C. Plastic-Deformation Analysis in Tube Bending[J]. International Journal of Pressure Vessels and Piping, 2000, 77: 751—759.
[6] 张敬文, 鄂大辛, 李延民, 等. 弯曲速度对弯管壁厚变化的影响[J]. 精密成形工程, 2012, 4(1): 35—39. ZHANG Jing-wen, E Da-xin, LI Yan-min, et al. Effects of Bending Velocity on the Change of Wall Thickness in Tube Bending[J]. Journal of Netshape forming Engineering, 2012, 4(1): 35—39.
[7] 林芳, 鄂大辛, 张敬文. 单元类型对有限元计算弯管截面畸变及壁厚变化的影响[J]. 精密成形工程, 2012, 4(3): 10—13. LIN Fang, E Da-xin, ZHANG Jing-wen. Effects of Element Types on Cross Sectional Distortion and Wall Thickness Variation in Finite Element Simulation[J]. Journal of Netshape forming Engineering, 2012, 4(3): 10—13.
[8] 樊子天, 鄂大辛, 陈吉生. 材料性能和相对壁厚对管材助推弯曲影响的分析[J]. 精密成形工程, 2013, 5(2): 16—19. FAN Zi-tian, E Da-xin, CHEN Ji-sheng. Analysis of the Influence of Material Properties and Relative Wall Thickness in Boosting Bending Process of Metal Tubes[J]. Journal of Netshape forming Engineering, 2013, 5(2): 16—19.
[9] 张敬文, 鄂大辛, 李延民, 等. 弯模间隙对5A06管弯曲横截面畸变及壁厚变化的影响[J]. 精密成形工程, 2012, 4(2): 19—22. ZHANG Jing-wen, E Da-xin, Li Yan-min, et al. Effects of Clearance on Cross Sectional Distortion and Wall Thickness Variation of 5A06 Tube[J]. Journal of Netshape forming Engineering, 2012, 4(2): 19—22.
[10] 戴莉, 方军, 程璐, 等. 材料参数对高强不锈钢管数控绕弯成形失稳起皱的影响[J]. 精密成形工程, 2017, 9(1): 91—95. DAI Li, FANG Jun, CHENG Lu, et al. Effects of Material Parameters on Wrinkling of High-Strength Stainless Steel Tube in Numerical Control Rotary Draw Bending[J]. Journal of Netshape forming Engineering, 2017, 9(1): 91—95.
[11] 魏文斌, 程旋, 余耀晖, 等. 基于自由弯曲技术的6061铝合金管的弯曲成形性能研究[J]. 精密成形工程, 2018, 10(4): 28—34. WEI Wen-bin, CHENG Xuan, YU Yao-hui, et al. Study on Bending Formability of 6061 Aluminum Alloy Tube Based on Free Bending Technology[J]. Journal of Netshape forming Engineering, 2018, 10(4): 28—34.
[12] 林艳. 薄壁管数控弯曲成形过程失稳起皱的数值模拟研究[D]. 西安: 西北工业大学, 2003: 78—83. LIN Yan. Numerical Simulation of Buckling during NC Bending of Thin-Walled Tubes[D]. Xi'an: Northwestern Polytechnical University, 2003: 78—83.
[13] 李恒. 薄壁管数控弯曲成形过程失稳起皱及成形极限的研究[D]. 西安: 西北工业大学, 2004: 154—160.LI Heng. Study on Instability and Wrinkle and Forming Limit in NC Bending Process of Thin Walled Tube[D]. Xi'an: Northwestern Polytechnical University, 2004: 154—160.
[14] YANG He, LIN Yan. Wrinkling Analysis for Forming Limit of Tube Bending Processes[J]. Journal of Materials Processing Technology, 2004, 152(3): 363—369.
[15] 俞汉清, 陈金德. 金属塑性成形原理[M]. 北京: 机械工业出版社, 1999: 42—45. YU Han-qing, CHEN Jin-de. The Principle of Metal Plastic Forming[M]. Beijing: China Machine Press, 1999: 42—45.
[16] WANG Xi, CAO Jian. Wrinkling Limit in Tube Bending[J]. Journal of Engineering Materials and Technology, 2001, 123(4): 430—435.
Analysis on Instability in Tube Bending Process Based on Total Theory of Plasticity
CHE Yi1, ZHAN Hong2, QU Jun-cen2, LIN Jun2
(1. AVIC Chengdu Aircraft Industry (Group) Co., Ltd., Chengdu 610073, China; 2. Southwest Technology and Engineering Research Institute, Chongqing 400039, China)
Based on the total theory of plasticity, the purpose of this paper is to study the outer side cracking and inner side wrinkling in the tube bending process, and analyze the causes and control methods. In this paper, the theoretical analysis method is used to establish the calculation formula of stress and strain of tube bending deformation, deduce the criterion of tube outer cracking and inner wrinkling, and verify the reliability of the prediction formula by experiment. Finally, based on the derived stress and strain calculation formula, according to the critical allowable deformation degree, the cracking criterion of the outer side of tube is established; based on the energy criterion, the formula of wrinkling in tube bending process is proposed, and the boundary parameters of wrinkling (instability) formula are determined. The experimental and theoretical results show that the calculation formulas of allowable/(ratio of bending radius to average radius of tube) under minimum wall thickness and allowable/(ratio of bending radius to average radius of tube) based on wrinkling (instability) calculation have high accuracy, which can be used to guide the design and optimization of tube-bending process parameters.KEY WORDS: tube bending; critical deformation; energy method; cracking; wrinkling
10.3969/j.issn.1674-6457.2021.03.013
TG386
A
1674-6457(2021)03-0112-06
2021-04-09
车移(1992—),男,工程师,主要研究方向为先进制造。
詹红(1992—),女,硕士,工程师,主要研究方向为精确塑性成形。

