基于改进DBSCAN算法的金相图像晶粒聚集检测方法

周 润，滕奇志

（四川大学 电子信息学院图像信息研究所，成都610065）

0 引 言

金相组织的定量分析是为了更加准确的检测材料的成分、显微组织等特性。其中包括平均晶粒度、粗大晶粒尺寸及粒度分布等。结构均匀的硬质合金材料，其强度、寿命均优于含有较多粗大晶粒或晶粒聚集的材料。因此，在晶粒度分析过程中，需提取图像中长径超过6微米的粗大晶粒，以及3个以上晶粒聚集区域。由于不同成分的合金材料将会应用在不同环境中，而含有较多粗大晶粒或晶粒聚集的合金材料，在恶劣环境下将出现疲劳现象，进而发生危险事故。早期的晶粒聚集检测工作是由专业人员目测聚集区域，并通过手动测量的方式进行。近年来，数字图像处理技术虽已逐步应用在金相分析领域，但针对晶粒聚集检测还没有较好的提取方法。本文实验中用到的金相图像是在光学显微镜30x、75x物镜下，由数字摄像头拍摄所得。如图1所示，一个视域的金相图像需提取晶粒密度相对较高的区域，如图1（c）中绿色标注区域。为提取目标区域，初步采用OTSU阈值分割算法分割出聚集区域，效果如图1（b）所示。此时，聚集周围有较多小型晶粒也被分割出来。进一步使用去噪算法剔除小型晶粒，效果如图1（c）。由于去噪后聚集区域内部一些晶粒被当作噪声剔除，无法较好的提取完整聚集区域。因此，上述方法不适用于晶粒聚集的检测。

从图像分析的角度看，聚集区域的晶粒坐标位置相对集中，因此考虑采用空间坐标聚类方法进行检测。常见的密度聚类算法有DBSCAN、OPTICS［1］等。本文在借鉴密度聚类算法的基础上，提出一种基于DBSCAN的金相图像晶粒聚集检测方法，并针对DBSCAN算法需确定Eps和MinPts参数的问题作出改进，使其能够根据图像，自适应地调整参数。同时使用k-d树数据结构对算法进行加速。实验结果表明，使用本文算法在不同放大倍数和不同聚集密度的情况下，均可以自适应地找出聚集区域且无需人为干预，具有较强的鲁棒性和稳定性。

图1 75x金相图像和预处理过后的图像Fig.1 75x metallographic image and pre-processed images

1 相关定义简介

1.1 DBSCAN

DBSCAN（density-based spatial clustering of applications with noise）算法由Martin Ester等人于1996年提出［2］，是一种典型的基于密度的聚类算法。相较于k-means等［3-4］其它类型的聚类算法，DBSCAN算法不需要事先指定类别数，且能够处理不同大小形状的簇，同时能够正确处理噪声点和离群点，常被应用于图像处理等领域。DBSCAN算法需要指定的基本参数：

（1）领域半径（E ps）。点p的领域表示为以p为中心、r为半径计算欧式距离的圆形区域。r即为领域半径。

（2）领域密度阈值（Mi nPt s）。 可简单表示为以点p为中心，E ps为半径的区域中，除点p之外其它点的数量。

DBSCAN算法通过以上参数确定领域密度。将所有数据点分为3类：

（1）核心点。在以点p为中心，E ps为半径的区域中，含有超过Mi n P t s阈值的点，则将点p称为核心点。

（2）边界点。在以点p为中心，E ps为半径的区域中，点的数量小于Mi n Pt s阈值，但点p落在其它核心点包含的区域中，则称点p为边界点。

（3）噪声点。孤立于核心点和边界点的其它点。

DBSCAN算法通过一定的距离度量方式，先找出所有数据点中的核心点，生成核心点列表。通过遍历核心点列表，将每个核心点的密度可达区域划分为一个簇，待所有簇划分完毕，将剩下的点标记为噪声点，算法结束。

1.2 k-d树

K-d树（k-dimensional Tree）［5］用于在k维空间为数据点建立索引。常见的KNN算法［6］中，使用线性遍历的方式查询目标数据。当数据点过多时查询时间复杂度较高，使用k-d树数据结构做索引，能够大幅提高查询效率。本文实验中所使用到的二维k-d树建树过程如图2所示。

图2 二维k-d树建树过程Fig.2 2-dimensional k-d tree building process

建树流程如下：

（1）确定划分域。首先计算所有数据点x坐标和y坐标的均值，再以该均值为基准，计算数据点在x方向和y方向上的方差，选择方差更大的作为划分域。方差更大表示在该坐标轴上的数据点较分散，如图2所示的建树过程，是以x轴作为划分域。

（2）确定切分点。将切分平面上的所有数据点，按照划分域为基准进行大小排序。选择排在正中的点作为切分点，并建立左、右子树。

（3）确定子空间。将切分好的两个子空间按照步骤（1）递归切分，直到某一子空间中只有一个或者没有数据点，则切分结束。

K-d树的查询过程如图3所示。以查询标星点p的最近邻点为例，查询其最近邻点需先在树中找到其直属的叶子节点q，并以点q作为临时最近邻点，计算出点p到点q的距离di s t，最后以点p为圆心，d i st为半径做圆，真正的最近邻点一定会在圆内，如点x。

图3 二维k-d树查询过程Fig.3 2-dimensional k-d tree query procedure

2 本文算法

2.1 预处理

因金相图像拍摄时受到亮度、景深、放大倍数等方面因素影响，直接使用OTSU阈值分割方法对图像提取晶粒时效果欠佳，如图4（b）所示。为解决此类问题，本文需对金相图像做预处理工作。图4（a）中金相图像的直方图如图5所示。从直方图中可以看出，图像的灰度值分布有明显的双峰形状，因此先使用对比度增强算法［7］调整晶粒和背景的对比度后，用直方图双峰法做初步的阈值分割，分割效果如图4（c）所示。可以看出，此时能将完整的聚集区域提取出来，但周围小型晶粒过多，直接使用聚类算法可能会有误分类。为进一步降低小型晶粒对聚类结果的影响，将上一次分割的结果映射回原图，再次遍历图像。此时只统计上次被分割区域中的最大和最小灰度值，并使用这两个灰度值作为阈值，使用OTSU双阈值分割算法再次分割图像，分割结果如图4（d）所示。此时聚集区域能被完整提取出来，且周围小型晶粒较少。

图4 阈值分割效果图Fig.4 Threshold segmentation renderings

图5 图像直方图Fig.5 Image histogram

2.2 改进的DBSCAN算法

DBSCAN算法用Mi n Pt s和E ps两个参数来描述聚类的密度阈值，将超过密度阈值的大集合聚成一个簇。因此，该算法对这两个参数的取值十分敏感，取值不当可能会导致聚类结果不正确。为此，很多国内外学者致力于研究自适应寻找Mi nPt s和E p s参数的方法。文献［8］根据数据点在每个维度密度分布不同的特点，提出一种自适应调整E p s的算法，该算法使用恒定的Mi n P t s；文献［9］根据确定密度峰值点的方式，提出一种自适应调整E ps的SALEDBSCAN算法，但该算法仍需要设置固定的Mi n P t s；文献［10］通过生成候选Mi nPt s和E ps列表，根据参数寻优策略，提出一种完全自适应的KANNDBSCAN算法，但该算法时间复杂度较高，在数据点规模较大时耗时较多。

鉴于以上问题，本文提出一种针对金相图像的自适应DBSCAN算法，其算法流程如下：

（1）根据金相图像特征，使用平均晶粒大小作为Mi nPt s，即：

式中，n表示图像中晶粒总个数，m表示整幅图像像素点总数。

在具体应用中，除聚集外还需要找出长径大于6微米的单个粗大晶粒，因此使用平均晶粒大小确定Mi nPt s比较合适。

（2）遍历图像生成候选核心点队列，以每个晶粒的重心作为候选核心点加入队列，并确定E ps，其表达式为：

式中，R i表示第i个晶粒的内切圆半径，取晶粒内切圆半径的五分之一作为每个候选核心点的E ps。

对于DBSCAN算法，在提取粗大晶粒后，继续将周围的小型晶粒聚为同一簇。而提取小型晶粒时，如果E ps过大，则将很多分散的小型晶粒聚为一簇。为减少此类情况，使用晶粒的自身特征来确定E ps较为合适。实验过程中发现，使用1／5R i作为E ps搭配Mi n Pt s效果较好，能够仅将晶粒自身及其周围小部分区域聚为一簇。

（3）用候选核心点队列和对应的E ps作DBSCAN聚类，记录聚类结果。若此时未完成整张图像所有数据点遍历，为判断剩余点为孤立的小型晶粒，则使用候选核心点列表中最小Eps作为参数进行下一轮聚类，直到遍历完所有数据点。

（4）将所有聚类结果标注回原图，算法结束。

2.3 算法总体流程

本文使用的金相图像待聚类像素点个数平均在十万左右。使用DBSCAN算法进行聚类时，由于每次寻找最近邻点时会重复遍历所有数据并计算每个点之间的距离，算法时间复杂度较高，运行时间较长。为此，本文使用二维k-d树数据结构划分数据区域并构建数据点索引，进而减少重复访问次数。算法整体流程如图6所示。

图6 算法流程图Fig.6 Algorithm flow chart

3 实验结果分析

本文算法采用C++语言实现，操作系统为Windows10，开发工具为Visual Studio 2010+MFC。为验证本文算法在金相图像数据集上的有效性和正确性，选择不同聚集密度、亮度、形状的图像，对比了手动标注图像、传统DBSCAN算法和本文算法。其中，所有手动标注图均由专业人员协助标注。具体实验过程和结果分析如图7、图8所示。

由图7、图8可以看出，对于聚集密度不同的图像，传统DBSCAN算法需要反复实验才能找到一个较合适的参数。如图7所示，为能包含整个聚集区域，适当调大了E ps和Mi n Pt s，但使周围一些小型晶粒被误聚类；在图8中，为使周围小型晶粒不被误判为聚集而适当调小参数后，可能导致聚集晶粒区域提取不完整。本文算法能够自适应地调整E p s，以将整个聚集区域找出且只包含少数小型晶粒。另外，使用F值（F-Sco r e）为聚集结果做定量分析［11］，F值的定义为：

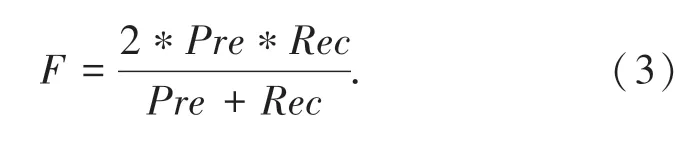
式中，Pre表示正确率，即正确聚类的个数占总聚类个数的百分比，Rec表示召回率，即正确聚类的像素点数占输入图像像素点总数的百分比。通过比较F值能够预估算法对于聚集效果的正确性。

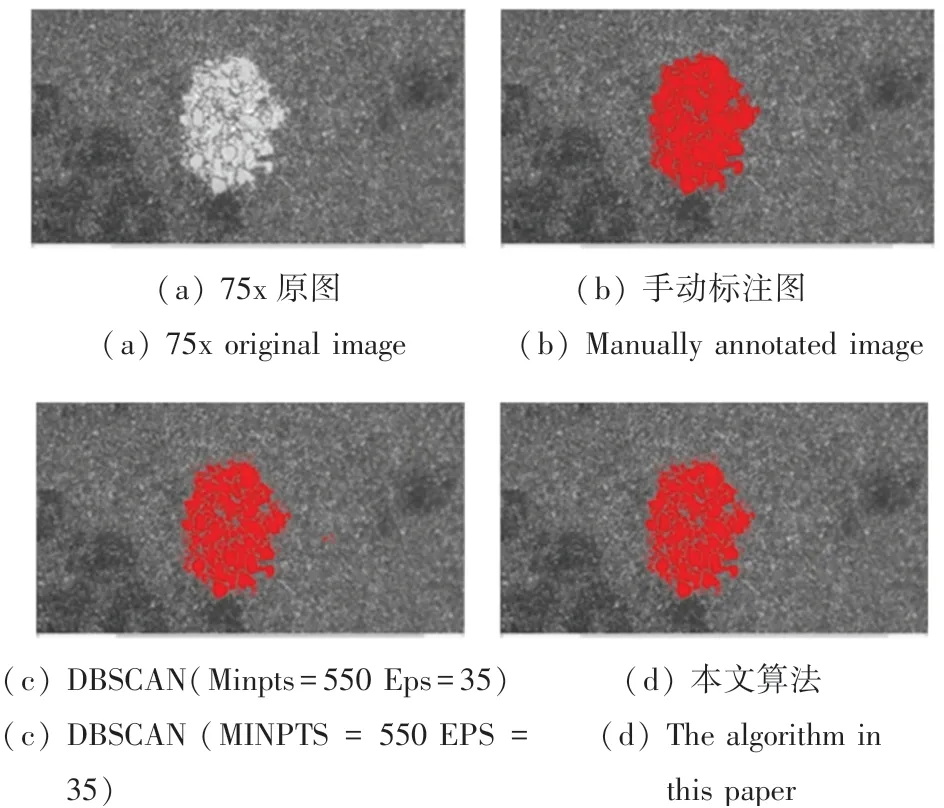
图7 实验结果对比图Fig.7 Comparison of experimental results

图8 实验结果对比图Fig.8 Comparison of experimental results

本文共测试不同放大倍数下共63张金相图像，在不同放大倍数下的F值对比和不同数据规模下的算法运行时间对比如图9、图10所示。

图9 不同倍数下F值对比结果Fig.9 Comparison results of F values under different multiples

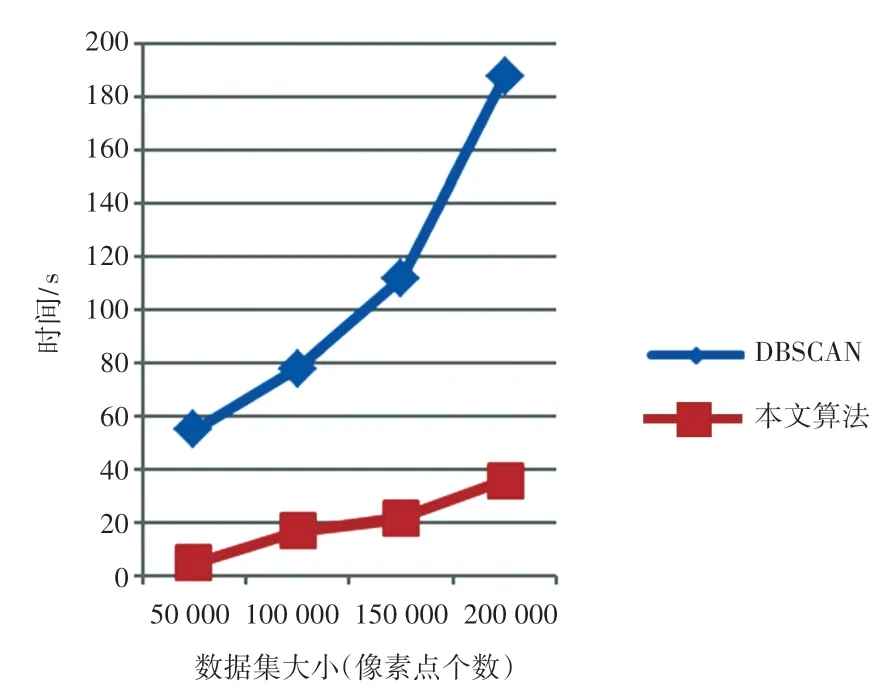
图10 不同数据集大小下时间对比结果Fig.10 Comparison results of time under different data set sizes

从图中数据对比可以看出，本文算法在聚集准确度方面优于传统DBSCAN算法，且通过k-d树加速后的算法时间复杂度更低，整个检测过程不需要用户干预，操作简洁方便。

4 结束语

本文提出一种基于改进DBSCAN聚类算法的金相晶粒聚集检测方法，该方法从密度聚类的思想出发，借鉴了许多国内外研究者对于自适应寻找DBSCAN最优参数的方法，提出了一种针对金相图像的自适应DBSCAN算法。实验证明，本文方法优于传统DBSCAN算法且无需人为设置参数，有更低的时间复杂度，能够准确便捷的完成检测任务。进一步的主要研究方向，在于如何让DBSCAN算法在聚类流程中自适应修改MinPts的值，以获得更加精确的聚类效果，并希望能将该算法嵌入实际工程当中，帮助工作人员高效完成任务。