科氏质量流量计测量含气液体流量关键技术综述

徐浩然，徐科军,2，张 伦，刘 文， 乐 静，黄 雅，刘陈慈

(1.合肥工业大学 电气与自动化工程学院，安徽 合肥 230009；2.工业自动化安徽省工程技术研究中心，安徽 合肥 230009)

1 引 言

科里奥利质量流量计(以下简称科氏质量流量计)是一种具有广阔应用前景的直接式质量流量测量仪表,同时,可以对密度、频率等物理量进行多参数测量[1]。但是,随着工业发展,越来越多的场合要求科氏质量流量计能够实现对含气液体流量的测量。造成含气液体流量,一方面是生产或者工艺的需要:在生产中需要气体均匀地混合在被测液体中,如生产香波,冰激凌等。另一方面是实际工况不可避免:在油料装车、食品批次加工和液体灌装等场合,需要对短时的批料流量进行测量,此时管道内会经历“空—满—空”的气液两相过程[2]。例如,在食品加工时,为达到卫生许可,在每一批料结束后、下一批料开始前,需要对管线上的残留物进行完全清理,这样在下一批料开始时会经历“空—满”过程。但是,含气液体流量测量是科氏质量流量计测量的难题,它对科氏质量流量计的驱动技术、信号处理技术都提出更高的要求。同时,由于流量原始测量误差大,还需要误差修正技术进行后期修正,来提高测量的准确度。

提高驱动信号的更新速度和稳定性可以更好地维持流量管振动,提高传感器信号的质量,为含气液体流量测量提供更好的基础;采用合适的信号处理方法可以减小含气液体流量下的原始测量误差;采用合适的误差修正技术可以修正含气液体流量下的测量误差。因此,科氏质量流量计测量含气液体流量主要包括3大关键技术,即驱动技术[3～6]、信号处理技术[7～15]和误差修正技术[16～25],众多学者从这3个方面进行研究,均取得了较好的进展。但是,科氏质量流量计在含气液体流量下的测量精度还无法满足工业实际应用中0.1级精度的测量要求,且目前鲜见科氏质量流量计测量含气液体流量方面的研究报道。为此,本文从驱动、信号处理、误差修正这3个方面进行比较综述,分析含气液体流量下,驱动、信号处理以及误差修正技术的难点,并针对难点总结出含气液体流量下最佳的驱动技术、信号处理技术和误差修正技术。探究含气液体流量原始测量误差大的原因以及采用修正方法修正后的测量精度依旧无法达到单相流测量精度0.1级的原因,为提高科氏质量流量计测量含气液体流量的准确度提供思路。

2 驱动技术

科氏质量流量计由一次仪表和二次仪表组成。一次仪表即科氏质量流量传感器;二次仪表即科氏质量流量变送器。科氏质量流量计工作的前提是维持一次仪表的振动,因此,驱动技术是科氏质量流量计的重要组成部分。科氏质量流量计中的驱动技术主要包括模拟驱动、数字驱动2大类。

2.1 含气液体流量下驱动技术的难点

科氏质量流量计一次仪表均有一个最佳振动幅值。流量管在最佳振动幅值下振动,具有最佳的测量性能且使用寿命最长[26]。在单相流下,流量管的阻尼比很小,较低的驱动能量就可以使流量管振动在最佳幅值。但是,测量含气液体流量时,由于气体与液体的密度差异,导致气体和液体之间会发生相对运动。这个相对运动带来的摩擦使流量管振动阻尼比剧增,消耗更多的驱动能量,如果变送器不能及时地提供足够的能量,流量管的振幅会减小甚至停振。提高驱动能量,即提高驱动电压的幅值,但在实际工业现场,出于本安防爆的考虑,驱动电路后级必须加入安全栅电路,对驱动电压和驱动电流进行限制。因此,在安全栅限制驱动能量的前提下,两相流发生时,流量管振动幅值就很难维持在单相流下最佳振动幅值的水平。此时,若要保证流量管平稳振动,就需要降低流量管的振动幅值。流量管具有选频特性,当驱动信号的频率等于流量管的固有频率且驱动信号的相位与传感器信号的相位匹配时,传感器信号以最大增益输出,驱动能量的利用率最高,流量管振动幅值最高,传感器信号最平稳。因此,含气液体流量下驱动技术的难点为:1) 在安全栅限制的范围内,尽可能提高驱动能量,使流量管维持在较平稳和较高水平的振动,即传感器信号维持在较平稳和较高的振动幅值;2) 尽可能快速地更新驱动信号,使驱动信号和传感器信号满足频率和相位的匹配关系。

2.2 数字驱动技术

模拟驱动[27,28]是基于正反馈的原理,利用模拟电路对传感器信号进行处理,得到驱动信号,从而驱动流量管。含气液体流量下,传感器信号的幅值、频率和相位波动剧烈,经过正反馈放大后,驱动信号的幅值、频率和相位也波动剧烈,驱动信号与传感器信号可能不在同一频率、相位上,导致传感器振动越来越小,甚至停振。因此,模拟驱动不适合测量含气液体流量。

而数字驱动的驱动信号全部由微处理器根据传感器信号的频率、相位、幅值信息来合成,进而驱动流量管振动,能够快速更新驱动信号,适合测量含气液体流量。根据实现驱动的微处理器不同,可分为基于DSP控制的数字驱动[29～32]和基于FPGA控制的数字驱动[33～35]。其原理框图如图1所示。

图1 数字驱动原理框图Fig.1 The schematic block diagram of the digital drive

2.2.1 流量管振动系统

流量管振动系统的传递函数为[36]：

(1)

式中：x(s)为驱动信号；y(s)为传感器信号；ωn为流量管固有频率；ξ为流量管阻尼比；k为放大系数。以CMF025型号传感器为例，ωn=2 π×135rad/s，取ξ=0.005，其幅频特性和相频特性如图2所示。

图2 流量管振动系统的幅频与相频特性Fig.2 Amplitude and phase frequency characteristics of flow tube vibration system

可见，流量管振动系统具有选频特性,当ω/ωn=1时，即驱动信号频率ω等于流量管固有频率ωn时,流量管振动幅值将达到最大，能量利用率最高。驱动信号相位与传感器信号的相位相差0°。但是，对于不同的传感器，驱动信号相位与传感器信号的相位可能存在180°的相位差。两相流下，数字驱动系统应能自动跟踪流量管固有频率的变化，在相位上具有0°或180°的补偿。在启振时，驱动幅值最大，随着流量管振动幅值的增大，驱动信号幅值自动调节,最终实现稳幅振动。

2.2.2 基于DSP控制的数字驱动系统

在基于DSP控制的数字驱动系统中,由于DSP具有强的运算能力,DSP除了需要执行驱动控制任务之外,还需要承担信号处理算法的任务。传感器信号经过ADC采样后,通过DSP实时计算信号幅值、频率和相位等关键参数。根据计算得到的频率和相位参数,由DSP确定所需合成的驱动信号的频率和相位,并控制DDS(直接数字式频率合成器)芯片产生对应的正弦信号,送入MDAC(乘法数模转换器)芯片的模拟输入端。同时,根据计算得到幅值参数,由DSP调用非线性幅值控制算法,计算出驱动信号需要的增益,并写入MDAC芯片的数字输入端,以控制驱动信号的幅值。MDAC芯片输出信号再经过功率放大后得到所需要的驱动信号,用于驱动流量管。

DSP为串行处理器,信号处理得到质量流量信息和更新驱动信号输出不能同时进行。DSP调用信号处理算法对ADC采集的一段数据进行处理,得到频率、幅值、相位信息后,才能更新驱动信号。对于文献[28]报道的基于DSP驱动的全数字式科氏质量流量变送器,ADC的采样频率为3.75 kHz,每500个点调用一次信号处理算法,因此更新一次驱动信号也需要500个点的时间,对于固有频率为102 Hz的传感器,约14个传感器信号周期更新一次驱动信号。这对于平稳单相流工况,由于流体较平稳,即使驱动信号更新周期较长,流量管也可维持平稳振动。而对于含气液体流量工况,流量管的振动每周期都会发生变化。驱动信号更新周期长,导致驱动信号与传感器信号之间无法实时满足频率、相位的最佳匹配,导致流量管振动幅值波动较大。

2.2.3 基于FPGA控制的数字驱动

在基于FPGA控制的数字驱动系统中,第1种设计方案是采用FPGA,同时承担驱动控制任务和信号处理算法的任务[33],但由于FPGA计算能力较差,会导致最终的质量流量测量精度较低。第2种设计方案是充分发挥FPGA的逻辑控制和并行执行的优势,FPGA只承担驱动控制任务,而信号处理算法的任务由另一片计算能力强的微处理器承担[34,35]。这样既可以保证驱动信号的快速更新,也可保证最终的质量流量计算精度。

FPGA为并行处理器,可以并行执行多个程序。对于文献[35]报道的基于FPGA和DSP双核科氏质量流量变送,FPGA控制外部ADC采集传感器信号,并与DSP进行数据通信。在控制ADC采样和与DSP进行数据通讯的同时,FPGA采用3点反向Lagrange插值算法和非线性幅值控制算法计算信号的频率、相位和幅值信息后,控制DDS和MDAC更新驱动信号并输出。

对于驱动信号的频率和相位参数,是检测到传感器信号的正过零点和负过零点均计算更新;对于驱动信号的幅值参数,只在检测到传感器信号的负过零点计算更新。因此,FPGA是半个传感器信号周期更新驱动信号频率、相位信息;单个传感器信号周期更新驱动信号幅值信息。与基于DSP控制的数字驱动系统相比,驱动信号的更新速度更快。这对于含气液体流量工况,即使流量管振动状态变化剧烈,也可较好地维持流量管振动。

驱动技术总结如图3所示。

图3 含气液体流量下驱动技术总结Fig.3 Summary of driving technology for measuring gas-containing liquid mass flowrate

3 信号处理技术

科氏质量流量计采用数字信号处理技术,直接决定了其测量精度、测量稳定性等性能指标。根据科氏质量流量计测量原理,流过流量管的质量流量与2路传感器信号时间差成正比,而时间差由相位差和频率换算而来。同时,频率直接反映了被测流体密度,而幅值反映流量管的振动状态,即是否工作在最佳振动幅值。因此,信号处理技术的关键是对两路传感器信号的相位差、频率和幅值3个特征量进行准确的测量。

3.1 含气液体流量下信号处理技术的难点

含气液体流量下,流量管内的流型变化复杂,气体对流量管产生的冲击,使得传感器信号波动剧烈,具体表现为正弦信号的3个特征量,即频率、相位和幅值波动剧烈。因此,信号处理算法需要能及时跟踪信号参数的变化,具有较好的动态响应性,才能处理含气液体流量信号。同时,由于频率变化,对于相位差计算直接依赖频率的计算精度的信号处理方法也不适合含气液体流量的测量。含气液体流量下流量管阻尼比剧增,模拟驱动技术下流量管出现停振现象,流量测量失去振动基础。为此,需采用数字驱动技术,通过快速跟踪传感器信号频率、相位和幅值的变化,来及时更新驱动信号参数,维持含气液体流量下流量管的振动。此时,要求信号处理算法整体运算量小,以便对信号参数的及时跟踪。因此,含气液体流量下信号处理技术的难点为:1) 信号处理算法响应速度快,能及时跟踪频率、相位和幅值的变化;2) 信号处理算法整体运算量小。

3.2 4种信号处理算法

由于含气液体流量下信号频率波动剧烈,对频率变化敏感的信号处理算法,如DTFT算法[12,15,32]、相关算法[13]、SGA算法[8]在计算相位差时会产生非常大的误差,因此,下面着重分析相位差计算不依赖频率影响的希尔伯特(Hilbert)算法[9～10,37～39]、正交解调算法[14]、复系数滤波算法[40]和过零检测算法[11,41,42]性能。

3.2.1 Hilbert算法

希尔伯特变换的测量原理是:基于传感器信号的正弦性,通过90°移相器,构造2路解析信号,利用正弦、余弦信号的性质,实现信号频率、相位和幅值的测量。

希尔伯特变换算法具有无迭代运算、无收敛过程、无需预知信号频率、计算精度高等优点。但是,一方面,其抗干扰能力较弱,计算精度受噪声干扰较大,要求信号具有较高的信噪比;另一方面,实现希尔伯特变换过程中,运算量大且存在端点效应,会使相位差计算结果两端出现“飞逸”现象。为了解决这2个问题,杨辉跃[37]、黄丹平[38]和刘维来[39]分别提出了基于奇异值分解降噪、基于小波变换和多相抽取滤波以及带通滤波的信号预处理方法,有效地增强了信号的信噪比,提高了相位差计算精度。张建国[10]等采用加窗函数的方法有效地抑制了端点效应,提高了相位差的计算精度。

3.2.2 正交解调算法

正交解调算法的测量原理是:利用一个接近传感器信号频率的信号对传感器信号进行正交解调,再通过低通滤波环节滤除高频分量,从而对幅值、频率和相位同时进行跟踪计算。

正交解调算法具有测频范围广、对谐波干扰抑制能力强和短时间内检测到频率偏移的优点。但是,该方法的计算精度受随机噪声的影响很大,方法实现的前提是对高频分量和噪声分量良好滤波,如果滤波效果不好将会带来较大的测量误差,因此,低通滤波环节的设计是该方法的关键环节,直接决定了该算法的测量精度。同时,低通滤波环节的延时也会对算法的响应速度产生一定影响。文献[14]设计了2种滤波环节,一种为FIR陷波器和60阶FIR低通滤波器相级联的滤波环节,另一种为FIR梳状滤波器和60阶FIR低通滤波器相级联的滤波环节,两种滤波方案均能实现对高频谐波噪声和随机噪声的良好抑制,保证正交解调算法的计算精度。

3.2.3 复系数滤波算法

复系数滤波算法原理:首先构建一个IIR低通滤波器,将滤波器进行角度偏移,从而构成复系数滤波器。在此基础上,将2路传感器输出信号通过复系数滤波器滤除负频率分量,此时,两路传感器信号均变为复数形式,通过相应运算即可得到传感器信号频率、幅值、相位差。

复系数滤波算法根据偏移角度的正负可对其进行分类,当偏移角度为正时,此时低通滤波器变为传感器信号正频率处的带通滤波器,此时构建的复系数滤波器为CBF(复系数带通滤波器);当偏移角度为负时,此时低通滤波器变为传感器信号负频率处的陷波滤波器,此时构建的复系数滤波器为CNF(复系数陷波滤波器);当将CBF与CNF结合时,即构成滤波器为CBF-CNF(复系数带通陷波滤波器)。

复系数滤波器由于抑制了传感器的负频率分量、且无需前置滤波器,因而具有测量精度高、运算量小的特点[40]。CBF与CNF相比,CBF抑制噪声能力更强,但其跟踪延迟较大。如针对一些长时间处于含气液体流量状态的工况,此时,噪声对于其测量精度是主要因素。因此,可以采用CBF抑制噪声,提高精度。而针对一些时间较短的空—满—空工况,此时,跟踪速度对于其测量精度是主要因素,因此,可以选择CNF加快跟踪速度,提高精度。而其余工况,则针对一些既有流量空—满—空变化、又有一段时间含气液体流量状态的工况,可以选择CBF-CNF进行滤波。

3.2.4 过零检测算法

过零检测算法的测量原理是:通过记录信号过零点的时刻,得到过零点间的时间间隔,进而求取信号频率和时间差,实现流量测量。

过零检测算法具有运算量小、无收敛过程和响应速度快等优点,但是该算法为时域信号处理方法,容易受谐波噪声和随机噪声的干扰,导致计算结果波动大。同时,过零检测算法利用的有用信息就是信号过零点的信息,过零点计算的精度直接决定了频率和相位差的计算精度。因此,在实际中侯其立等[41]采用将带通滤波和二次Lagrange插值拟合相结合的数字式过零检测方法,实现对噪声的良好抑制与过零点的精确提取,提高了频率和相位差的计算精度。郑德智等[42]提出将多抽一滤波的有限冲击响应滤波器和切比雪夫曲线拟合相结合的数字式过零检测方法,也实现了对噪声的良好抑制与过零点的精确提取,提高了频率和相位差的计算精度。

信号处理技术总结如图4所示。

图4 含气液体流量下信号处理技术总结Fig.4 Summary of signal processing technology for measuring gas-containing liquid mass flowrate

4 误差修正技术

含气液体流量下,测量误差与多种因素有关,表现为复杂的非线性和非单调性。这使得对含气液体流量下的测量误差难以从机理方面建模。人工神经网络在传感器建模、预测和控制方面的应用非常广泛。神经网络在进行建模预测时,只需要根据样本数据建立模型,即可根据模型对未知数据进行预测。利用神经网络具有逼近任意非线性函数的能力,可以模拟实际系统的输入输出关系。

4.1 含气液体流量下误差修正技术的难点

含气液体流量下,被检表由于受到气体的干扰,测量误差复杂,特别是当气体含量较高时,液体流量测量误差表现出非线性、非单调性的特点。文献[43]采用时间序列分析方法,分析了含气液体流量下流量序列的变化规律,建立了流量序列ARAM数学模型,模型表明,流量序列由稳定分量和波动分量组成。由于流量序列存在稳定分量,因此,采用误差修正方法对原始测量误差进行修正来提高测量精度是合理的。但是,由于稳定分量与流量和密度降之间的关系是非线性的,因此,即使采用误差修正技术也是无法得到完全修正的。同时,波动分量造成的误差也只能通过平均处理在一定程度上减小。由于这2部分误差的存在,因此,含气液体流量下科氏质量流量计的测量精度无法达到单相流的测量精度。含气液体流量下修正误差是修正稳定分量,由于误差非线性,必须采用非线性建模预测误差。同时,一般用来建模的数据是有限的,而科氏质量流量变送器在线预测时会对不同流量点、不同含气量进行误差预测并修正,这要求采用的误差修正方法不仅能对训练过的数据进行预测,还能对没有训练过的数据进行良好的预测,即具有良好的泛化能力。因此,含气液体流量下误差修正技术的难点为:1) 原始测量误差非线性、非单调性,需进行非线性建模预测;2) 误差修正方法具有良好的泛化能力。

4.2 测量误差和分析

为了获取含气液体流量下科氏质量流量计原始测量误差,探究误差大的原因,采用基于FPGA和DSP双核科氏质量流量变送器匹配上海一诺仪表有限公司(以下简称上海一诺)DN25微弯传感器进行含气液体流量实验,变送器中驱动技术为FPGA控制的数字驱动技术、信号处理技术采用过零检测算法[24]。

4.2.1 实验过程与结果

含气液体流量实验装置由水路通道和气路通道组成[24,25]。水路通道包括水泵、气液混合器、被测科氏质量流量计、换向器和称重装置等。气路通道包括空压机、气体罗茨流量计和气体玻璃浮子流量计等。实验装置通过PLC控制各器件动作,协调完成整个实验过程。当进行含气液体流量实验时,水从水箱中抽出,通过气液混合器与空气压缩机产生的空气混合后,形成含气液体流量,然后,流经被测科氏质量流量计,最终流入称重装置,称重装置的称重值作为标准值。通过比较科氏质量流量计的测量值与称重装置的称重值,即可得到科氏质量流量计在含气液体流量下的原始测量误差。

对于含气液体流量,通常使用含气量(GVF)来表征含气液体流量中的气体含量大小。在实际测量中,气体体积流量不易获取,变送器无法在线实时计算GVF。但是,科氏质量流量传感器信号的频率反映了被测混合流体的密度D1[23]。变送器再根据已知的单相液体的密度D0,就可以计算出密度降Dd为：

(2)

被测流体密度的变化情况在一定程度上反映了液体和气体相对含量的大小。因此,可以用实测的密度降来表征含气量的大小。

具体的实验过程如下：

先固定液体流量为某一数值,如100 kg/min。改变加气量,使密度降以3%左右的间隔在0～35%的范围内变化,进行一轮含气液体流量实验。再改变液体流量,使液体质量流量以10 kg/min的间隔在30～100 kg/min的范围内变化,重复改变加气量的步骤,得到不同流量、不同含气量下,科氏质量流量计含气液体流量测量误差。

变送器匹配上海一诺DN25微弯传感器在含气液体流量下的原始测量误差如图5所示。可见,当水流量在30～100 kg/min变化、密度降在0～35%变化时,含气液体流量测量误差最大达-50%。

图5 含气液体流量下原始测量误差Fig.5 Original measurement errors of gas-containing liquid mass flowrate

4.2.2 原始测量误差原因分析

含气液体流量下,科氏质量流量计采用了合适的驱动技术和信号处理技术,但原始测量误差依然较大。科氏质量流量计的原始测量误差主要表现为2个方面:

1) 气相与液相的相对运动导致的误差：科氏质量流量管做横向振动时,会带动流体也做横向振动。由于气相与液相的密度不同,流体做横向位移时,气相与液相之间会产生相对运动,使得最终作用于流量管壁的科氏力较小,进而导致负的误差出现。

2) 流体的可压缩性导致的误差：当液体中混入气体后,流体就变得可压缩。可压缩流体流经管道时,会自主产生横向振动。即使流量管不做横向振动,流体流经流量管时也会以一定频率做横向振动,该频率大小与声在流体中传播的速度和流体密度有关。当流量管横向振动时,流体本身的振动会对流量管的振动产生影响,使得作用于流量管管壁上的科氏力较大,从而导致正的误差出现。

影响误差变化的因素主要为以下3点。

1) 流量管的原因：a) 流量管的形状。不同形状的流量管,流体流动的路径不同,两相流下测量误差不同。b) 流量管的安装位置。水平安装与垂直安装,流体流动时受重力的影响不同,两相流下测量误差不同。c) 流量管的材料。相同形状而不同材质的流量管,两相流的测量误差也不同。

2) 流体的原因：a) 气液融合。气体和液体在流动过程中可能发生融合现象,使测量结果出现误差。b) 干扰项。测量含气液体流量时,气体是干扰量,标准值为水的称重值,测量值为流量管中混合的含气液体流量体的质量流量,这会对测量结果产生误差。c) 流体状态。不同含气量下,气液两相的混合程度不同,气体的存在形式可能是气泡,也有可能是层流,这会对测量结果产生误差。d) 气体的可压缩性远远大于液体,可能造成误差。

3) 压强、温度等原因：含气液体流量下科氏质量流量计原始测量误差大的根本原因主要是气液两相的相对运动以及流体的压缩性。合适的驱动技术和信号处理技术只能在一定程度上提高测量精度和改善原始测量误差的规律性,提高测量的重复性,为后续的误差修正打下良好基础,以此提高整体的测量精度,但并不能从根本上减小科氏质量流量计的原始测量误差。

4.3 误差建模与修正

神经网络具有多种算法,为了得到更为准确的含气液体流量误差模型,对BP神经网络[23]、RBF神经网络[17～19]、Elman神经网络[25]、支持向量机[22,24]4种误差修正技术进行分析并建模,得到误差模型后,离线对质量流量进行修正,比较4种网络的性能。预测的模型如图6所示。输入变量为实测质量流量和实测密度降,误差模型将预测出相应的误差,根据预测的误差对实测的质量流量进行修正,便可以得到修正的液体质量流量。

图6 预测模型Fig.6 The predicted model

4.3.1 BP神经网络

具有偏差和至少1个S型隐含层加上1个线性输出层的网络可以逼近任何在闭区间连续的函数。这里采用1个输入层,1个隐含层,1个输出层对科氏质量流量计含气液体流量下的测量误差建模。BP网络模型如图7所示。

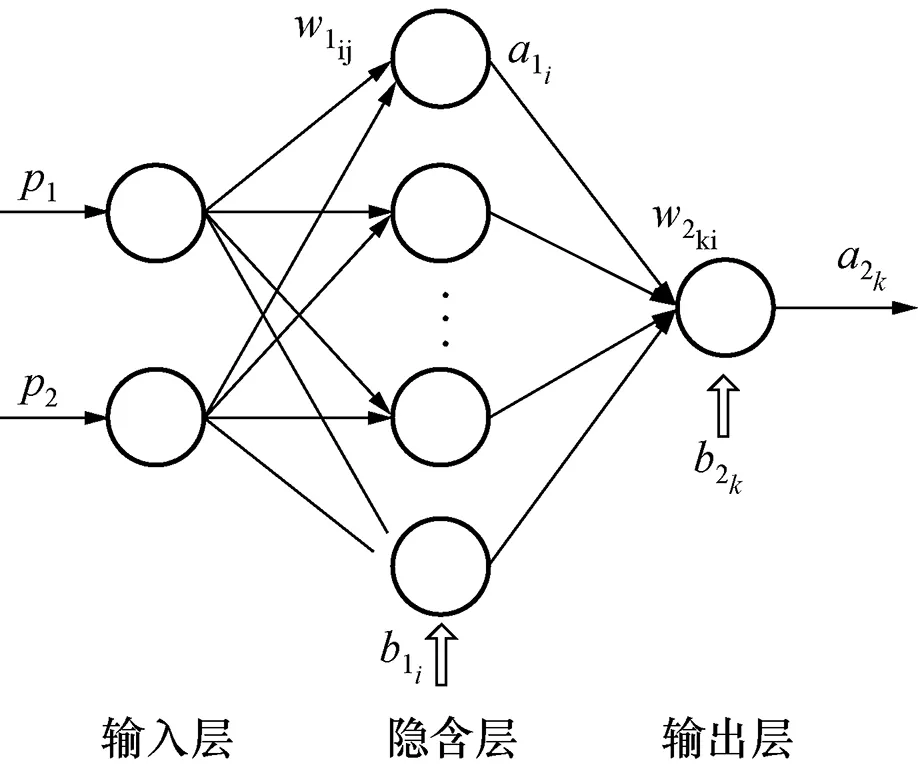
图7 BP神经网络结构Fig.7 The structure of the BP network

含气液体流量测量误差主要受流体流量和气体含量的影响,故将BP网络的输入层节点数设置为2，其中p1代表的是质量流量值，p2是流体密度降值；输出层节点数设置为1，表示测量误差。

BP神经网络中,隐含层第i个节点的输出为：

(3)

式中：r为BP网络输入层的节点个数,即r=2；i=1,2,…,s1,s1为BP网络隐含层的节点个数，该值通过仿真确定；w1ij为输入层到隐含层间的权值；b1i为隐含层的阈值。隐含层的激活函数选择Sigmoid函数。

输出层的节点输出为：

(4)

式中：w2ki为隐含层到输出层间的权值；b2k为输出层的阈值；k=1,2,…,s2,s2为输出层的节点个数，s2=1。对于输出层,激活函数为线性函数。

设网络输出的目标值为tk，取误差函数为：

(5)

网络训练时，是按梯度下降法，不断调整网络权值W和阈值B，使误差最小。

4.3.2 RBF神经网络

RBF神经网络是单隐含层的3层网络,是一种以函数逼近理论为基础的前向网络。RBF网络与BP网络最大的区别是,其采用径向基函数作为隐含层的激活函数,且激活函数是以权值向量和输入向量间的欧式距离作为自变量。RBF神经网络的结构如图8所示。

图8 RBF神经网络结构Fig.8 The structure of the RBF network

径向基函数为：

r(n)=e-n2

(6)

距离函数为：

(7)

式中：w1i为第i个隐含层节点与输入层间的连接权值;r为输入层节点数。

隐含层第i个节点的输入为：

(8)

式中：b1i为隐含层第i个节点的阈值。阈值b1可以用来调节函数的灵敏度,即输出对输入的响应宽度。

隐含层第i个节点的输出为：

a1i=exp(-ki2)

(9)

输出层的输入为各隐含层节点输出的加权求和,且输出层的激活函数为线性函数。

4.3.3 Elman神经网络

Elman神经网络是一种反馈型网络,网络结构如图9所示。Elman神经网络一般包含4层,即输入层、隐含层、承接层和输出层。Elman神经网络与BP神经网络相比,多出一个承接层。隐含层的输出不仅作为输入送至输出层,还通过承接层反馈至隐含层的输入,因而承接层是对隐含层输出的延迟存储。

图9 Elman神经网络结构Fig.9 The structure of the Elman network

对于k时刻,隐含层的输出为：

A1(k)=f1(IW×P(k)+LW1(k)×CN(k)+b1(k))

(10)

式中：P为输入向量；IW为连接输入层到隐含层的权值向量；b1为隐含层的阈值向量，LW1为连接承接层到隐含层的权值向量；CN为承接层的输出向量。

CN(k)=A1(k-1)

(11)

隐含层激活函数f1(n)仍然取Sigmoid函数。

k时刻输出层的输出为：

A2(k)=f2(LW2(k)×A1(k)+b2(k))

(12)

LW2为连接隐含层到输出层的权值向量，b2为输出层的阈值向量。输出层的激活函数f2(n)取线性函数。

Elman神经网络也采用BP算法进行权值修正,误差函数取均方差函数。

4.3.4 支持向量机

支持向量机是一种基于统计学习理论的机器学习算法,与传统的基于经验风险最小化原则的机器学习算法,如神经网络不同,支持向量机是基于结构风险最小化原则,考虑的是经验风险和置信界之和的最小化,保证了学习机器具体良好的泛化能力。

支持向量机模型结构如图10所示。输入向量(x1,x2,…,xn)通过核函数k(x,xi),映射到m维特征空间,然后在此特征空间构造一个线性模型来进行预测。特征空间的线性模型即：

图10 支持向量机网络结构Fig.10 The structure of the SVM

y=wx+b

(13)

式中：w=(w1,w2,…,wm)为权值向量;b为偏置项;m为支持向量的数目。

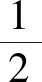
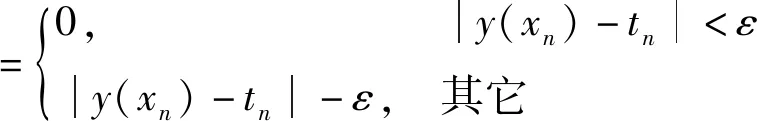
(14)

因此，优化问题可以写成：

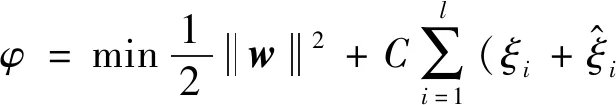
(15)

式中：l为训练样本的数量;C为正则化常数。

式(16)为带条件约束的最小化问题,通过引入拉格朗日乘子,构造拉格朗日函数,解对偶问题,得到优化问题的解w和b。因此,线性模型可以写成：

(16)

SVM常见的核函数有线性函数、多项式函数、RBF径向基函数、sigmoid函数等。RBF径向基函数为目前应用最广泛的核函数,本文也采用RBF径向基函数为核函数,故最终SVM模型的输出为：

(17)

式中：g为RBF径向基核函数参数；x为输入向量；xi为支持向量。

4.3.5 4种神经网络对比

分别采用4种网络对相同的含气液体流量的样本数据进行训练建模和离线修正。由于所选择的神经网络最终需要在微控制器上实时实现,以便对含气液体流量下的测量误差进行在线修正。这时不仅仅需要考虑神经网络的修正精度,还需要考虑网络的运算复杂度。如果网络过于复杂,运算量过大,将无法在微控制器上实时实现。神经网络实现的运算量主要与网络的结构、隐含层节点数等因素有关。文献[23,24]确定了BP、RBF、Elman这3种神经网络实现时最佳的隐含层节点数,与支持向量机[22,25]一起对4.2.1节的原始误差建立模型,从修正精度和网络运算复杂度两方面分析对比4种误差模型,结果如表1所示。

表1 4种神经网络的对比Tab.1 Comparison of four neural networks

可见,BP、RBF、Elman这3种神经网络误差模型,对含气液体流量测量误差离线修正效果相当。RBF神经网络需要20个隐含层节点,并且在求取隐含层输入时,需要求取距离,引入了开方运算,加大了网络的运算量。Elman神经网络需要25个隐含层节点数且在结构上多了1个承接层,所以不仅在网络训练时加长了训练时间,在网络实现时,也加大了运算量。BP神经网络相较于这两种网络,网络结构简单,在求取隐含层的输入时,不需要求取距离,且所用的隐含层节点数最少,仅需要15个隐含层节点,因而网络运算量较小。支持向量机方法在网络实现时就是一个线性函数,不需要隐含层节点,不存在复杂运算,且修正精度优于其它3种网络结构。

从分析结果可知,支持向量机算法的修正精度最高、运算复杂度最小,其离线修正结果如图11所示。因此,采用支持向量机算法对原始误差数据建模,并进行在线修正实验。

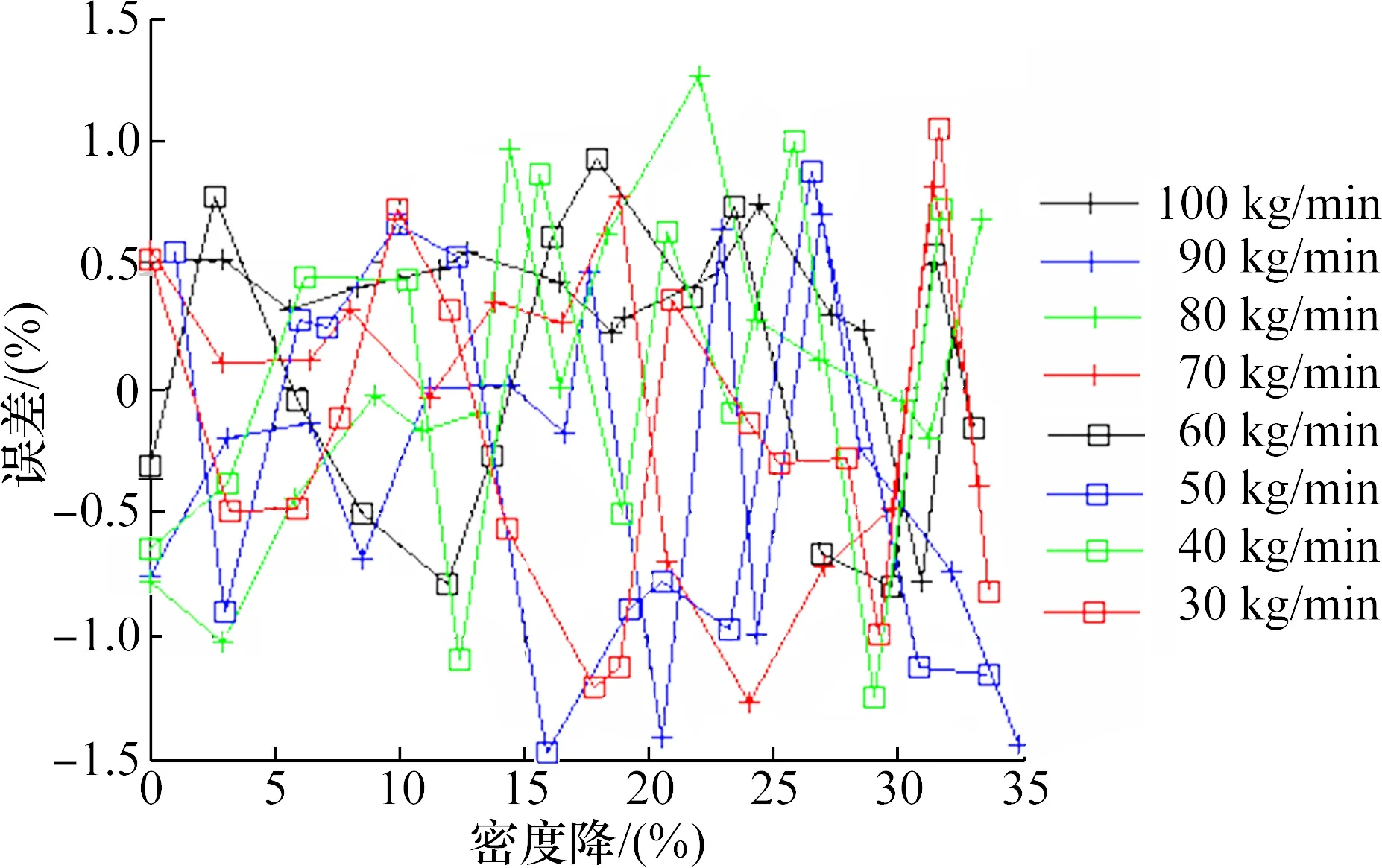
图11 离线修正后的测量误差Fig.11 Off-line corrected measurement error

4.3.6 在线修正

将已建立的测量误差模型的参数植入到研制的双核变送器中,实现对含气液体流量测量误差在线实时修正。为了严格考核在线修正的效果,并验证支持向量机对新的输入样本的预测能力,选择与建立误差模型时不同的液体流量点进行含气液体流量在线修正实验。具体选择的水流量点为35 kg/min、45 kg/min、55 kg/min、65 kg/min、75 kg/min、85 kg/min和95 kg/min。对于上海一诺DN25微弯型科氏质量流量传感器,在线修正后的结果如图12所示。

图12 含气液体流量在线修正后的测量误差Fig.12 Errors after on-line correction of gas-containing liquid flow

可见,当水流量在35～95 kg/min变化时,对于上海一诺DN25微弯型科氏质量流量传感器,当密度降小于15%时,修正后最大测量误差在±1%以内;当密度降在15%～35%时,修正后最大测量误差在-2.5%～2%以内。

误差修正技术总结如图13所示。

图13 含气液体流量下误差修正技术总结Fig.13 Summary of error correction technology for measuring gas-containing liquid mass flowrate

5 结束语

1) 在驱动技术方面,传统模拟驱动无法维持流量管振动;数字驱动可以较好地维持流量管振动,但对于不同微处理器控制的数字驱动,驱动信号的更新速度不同。基于DSP控制的数字驱动,由于驱动信号的更新速度较慢,驱动效果相对较差;基于FPGA控制的数字驱动,信号处理算法采用DSP实现,驱动信号的更新速度快,驱动效果最佳。虽然驱动技术不是含气液体流量原始测量误差大的原因,但好的驱动方法可以增强原始测量误差的规律性,为后续的误差修正进一步提高测量精度奠定基础。

2) 在信号处理技术方面,正交解调算法由于低通滤波环节产生的延迟,响应速度较慢;Hilbert算法和复系数滤波算法实时实现时,运算量大,无法保证驱动信号参数的及时更新,会导致数字驱动效果较差。而过零检测算法运算量小,易于实现,可以保证驱动信号参数的及时更新,提升数字驱动效果,一定程度上提高含气液体流量下传感器信号的质量,更适合含气液体流量的测量。

3) 在误差修正技术方面,BP神经网络、RBF神经网络和Elman神经网络的修正效果相当。但支持向量机方法在修正精度和网络运算复杂度两方面均优于BP神经网络、RBF神经网络和Elman神经网络。因为支持向量机以统计学理论为基础,具有严格的理论和数学基础,泛化能力强,而神经网络结构设计需要依赖于设计者的经验知识和先验知识。

4) 测量含气液体流量的原始测量误差大的根本原因是气液两相的相对运动和流体的可压缩性。表征含气液体流量的时间差序列模型由稳定分量和波动分量组成。误差修正技术可以修正稳定分量,但稳定分量是非线性的,无法完全得到修正;同时,波动分量也只能在一定程度上减小。因此,科氏质量流量计在测量含气液体流量时,无法达到单相流的测量精度。但是,合适的驱动技术、信号处理技术、误差修正技术对于科氏质量流量计测量含气液体流量是有效的。