磁悬浮列车地面效应的数值仿真分析研究

高士浩，刘振国，金武飞，曹 翀，郝瑞超

（1.北京机械工业自动化研究所，北京 100120；2.北京机械工业自动化研究所有限公司，北京 100120）

0 引言

在列车高速运行过程中，由于地面和车体底部之间的空气会被压缩，形成较大的压力，进而对磁悬浮列车的受力情况产生影响[1]，这就是我们通常所说的地面效应。经过反复的试验和检测，结果表明：磁悬浮列车的气动性能受到地面效应的影响非常大。之前由于列车的速度没有那么快，地面效应对列车的影响也没有那么大，并没有受到人们的高度重视[2]。近年来，随着高速列车的出现，列车的速度在不断的提升，作为一个新型的研究课题，地面效应对高速列车的影响开始被人们重视。列车的升力、阻力以及车体表面的压力，都会因地面效应的存在而发生明显的变化。乘坐的舒适性，车体的疲劳性破坏也会受到地面效应的影响[3]。

本文主要借助CAD进行车体二维建模，然后划分网格，再借助于有限元分析软件Fluent进行数值分析，分析的重点在不同的速度，地面是静止还是移动的情况下，列车的阻力系数、升力系数以及监测点的压力系数是如何变化的，他们是如何受到地面效应的影响的，进而通过分析得出地面效应对磁悬浮列车的气动影响结论。

1 磁悬浮列车的空气动力学研究方法

本文采用数值仿真的试验方法来研究磁悬浮列车气动力问题，其中有限元分析法在磁悬浮列车空气动力学问题上较其他方法更简便、更有优势，是目前研究流体力学主要的计算方法[4]。所以本文也采用了有限元分析方法，并借助大型有限元分析软件ANSYS中的ICEM CFD（以下简称ICEM）和Fluent来进行建模和数值计算分析。考虑磁悬浮列车运行过程中的实际情况，在计算分析时我们选择了均匀风比较合适，此次试验应用RANS方法进行磁悬浮高速列车的地面效应研究，选取的湍流模型为Realizable k-ε。选取合适的湍流模型对磁悬浮列车的空气动力分析至关重要。对比标准的k-ε模型，Realizable k-ε模型对正应力进行了数学约束，避免了可能出现的负正应力、涡粘系数计算公式中的Cp变成了可变数字，计算精度高，适合应用于计算磁悬浮高速列车底部复杂的数值计算。研究的总体步骤如下：

1）使用Auto CAD进行物理建模，建立TR08型磁悬浮列车的二维切面模型，并在CAD中进行模型细节处理，测量位置坐标等所需参数。

2）将模型导入商业软件ANASYS中的ICEM，对所建立的二维模型利用自然网格方法进行网格划分并检查网格质量、长宽比等参数，导出网格。

3）将ICEM导出的的网格导入Fluent软件中，选用湍流稳态进行定常流场计算。

4）后处理和结果展示。

2 k-ε双方程湍流理论

按照Reynolds时均方法，建立湍流时均匀运动基本方程组，它包括连续性方程和运动微分方程。

1）连续性方程：

由不可压缩均质流体运动的连续性方程得：

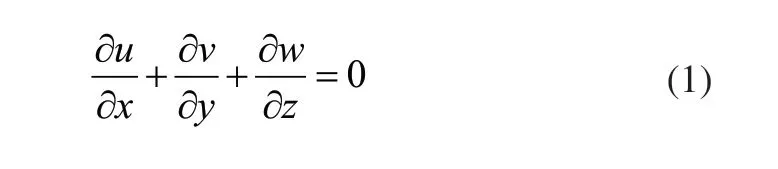
在湍流流动中，u、v、w 均为瞬时值，按照Reynolds时均法则，它们可以表示为时均值和脉动值之和，即：

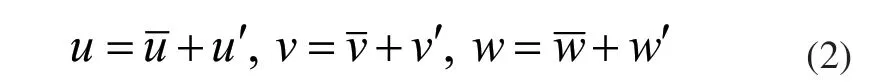
将以上方程代入连续性方程，并作时均运算得：

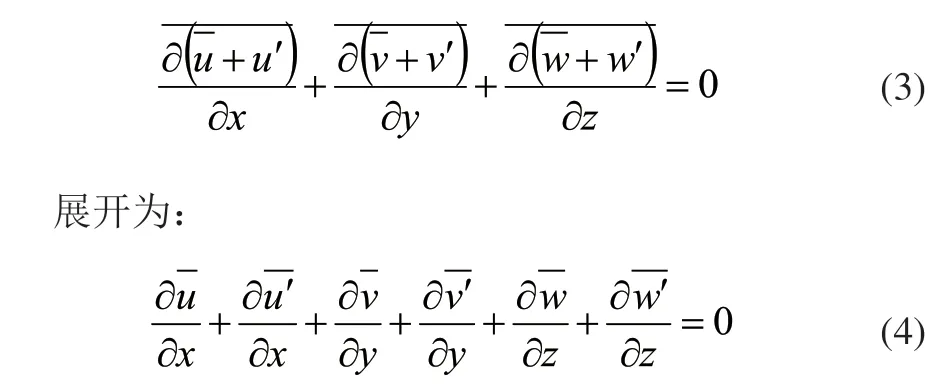
根据时均法则，脉动项的时均值为零，即上式可写为：

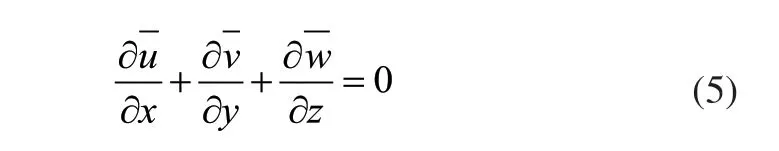
2）运动微分方程：

不可压缩粘性流体的运动方程X方向的方程式为：

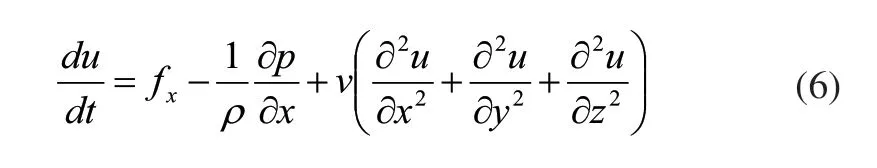
对于湍流，方程中各流动参数均为瞬时量，作类似于连续性方程的处理，有：

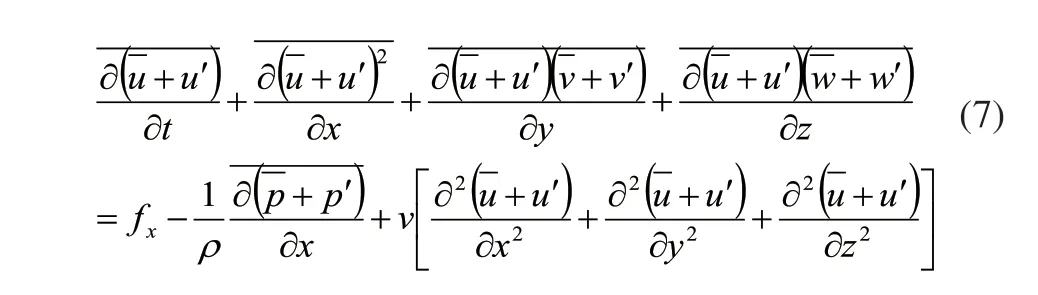
把左边的脉动分量的乘积移到等号右端，其他两个方向的推导与之类似，所以我们可以把三个方向的运动方程用直角坐标系中的张量符号表示为：

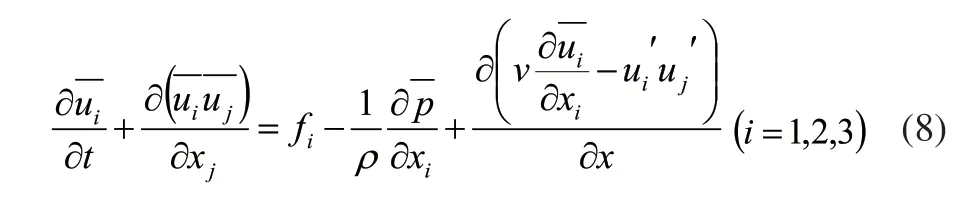
为了与通用的对流-扩散方程保持形式上的一致，以流体密度ρ乘上式各项，可得：

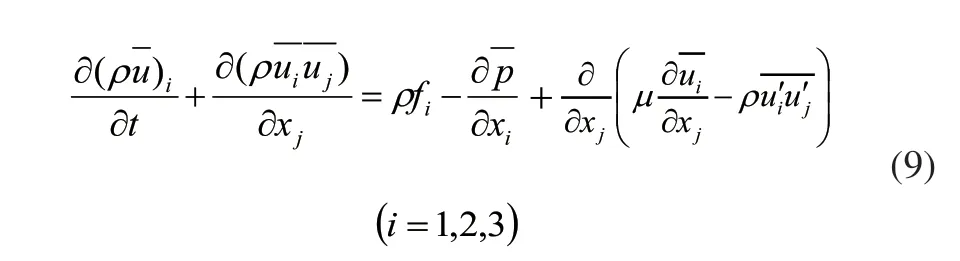
此式即为不可压缩粘性流体湍流时均流动的运动方程，也称为Reynolds方程，即雷诺方程。

从上述方程的导出过程可知，雷诺时均方程与不可压缩粘性流体的运动方程相比，增加了一项称为雷诺应力或湍流应力。当i≠j时，雷诺应力为切应力；当i=j时，雷诺应力为压应力。雷诺应力代表了由于湍流脉动对时均流动产生的影响。

为清楚表示涡粘性系数法的基本思想，将不可压缩流体的N-S方程和雷诺方程写在一起。

张量形式的N-S方程：

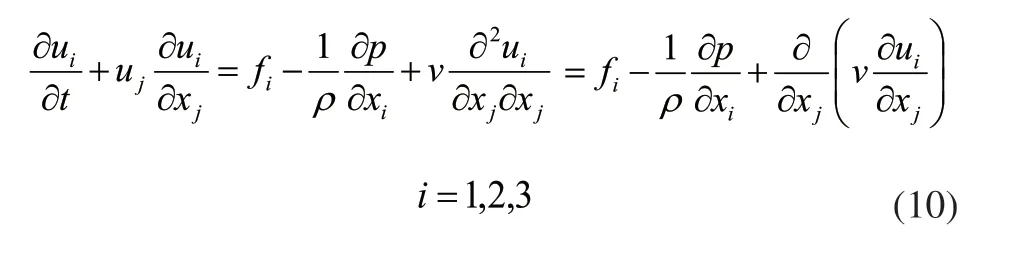
张量形式的雷诺方程为：

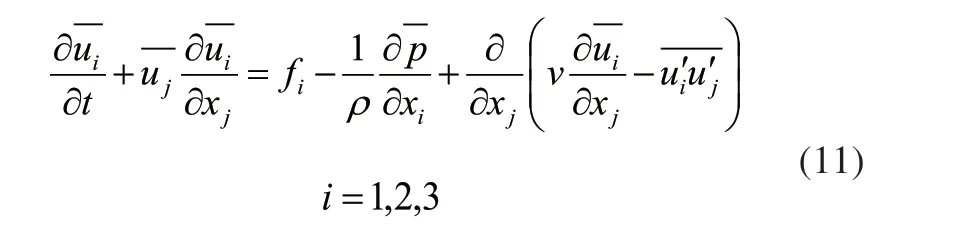
不难看出，它们之间的差别除去时均表述外，仅在最后一项。而粘性应力与雷诺应力具有相同的量纲，实际上，表示湍流脉动所形成的附加应力，该应力可以考虑与粘性应力存在着某种联系。从这个角度出发，将其表示为：

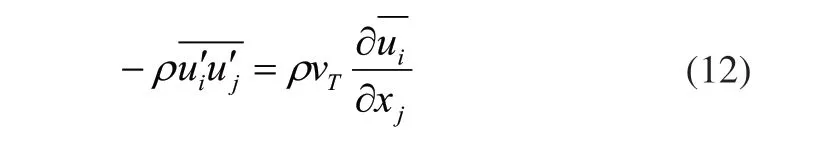
式中，vT称为湍流的涡粘性系数。因此，雷诺方程就可以表示为：

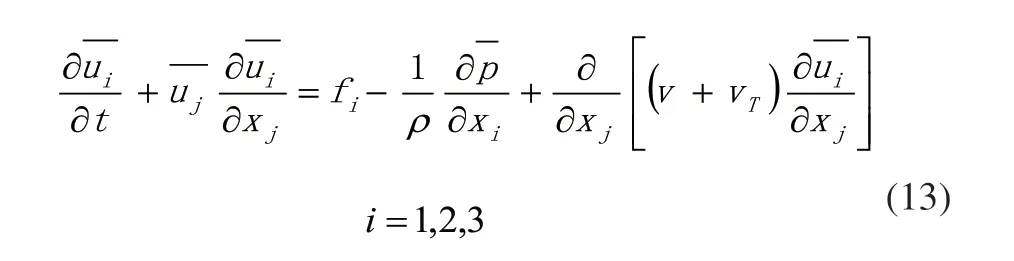
如果去掉时均符号，它与N-S方程的区别仅在于粘性力项前面的系数由原来的v变成了v+vT。

3 模型的建立与数据运算

3.1 模型建立

本文车型选用TR08型磁悬浮列车，实验采用1:1完全比例的3节编组的磁悬浮列车模型作为研究对象，因本课题主要研究的是地面效应对磁悬浮列车表面的阻力及车体的升力问题，横风问题并不在此实验的研究范围，所以可以简化为二维的模型，将车长设置为90m，车高设为3.2m。计算域设为290m×40m，由于考虑地面效应的影响后，对头车、中间车体和尾车的气动力分析影响结果是不尽相同的，所以将车体分成车头、车体、尾车三段，是为了方便以后分析地面效应对三节车体不同的影响，为后续的结果分析提供方便，计算模型如图1所示。

图1 车体模型

将建立好的模型导入到ICEM中，采用计算域为290 m×40m，在计算域内建立Part，切分计算域并进行网格划分。边界条件设置为：入口设置为速度入口，分别为50m/s、80m/s、120m/s，出口为压力出口，计算域的上方为滑移壁面，地面则要根据实际的测量情况设置为静止地面或者移动地面。本实验网格采用三角形网格，在整个车体的表面都需要加边界层，车体表面的边界层设为8层，高度为1mm，增长率为1.2，最大网格设置为2000，第八层边界层与和他接触的计算域网格接触良好，车头和车尾的位置要对网格进行加密处理，总的网格数控制在20万左右，计算模型网格如图2所示。查看网格质量，大部分在90%～100%，网格质量良好，可以导入Fluent中进行数值运算。

图2 整体网格图

本试验主要是研究地面效应对磁悬浮列车的气动影响，所以采用对比实验，考虑地面静止或者移动的情况下磁悬浮列车的气动力分析，其次要分析不同的风速下的情况，因此本试验设置了车速为50m/s、80m/s、120m/s在静止地面和移动地面六种工况来进行研究。

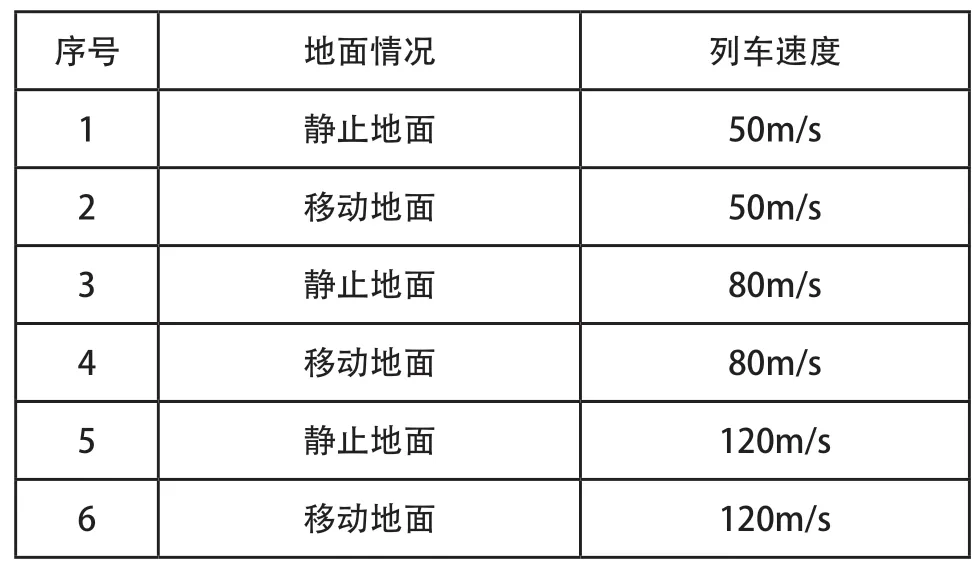
表1 研究工况

从图3可以看出，在六种不同的工况下，列车周围整体的流场大致是一样的：在车头的最前点处，逐步向上分析，气流的速度逐步增大，在车头跟前车天线交接处，速度又逐渐降低，主要原因是流场受到了天线前端的阻挡，使得速度降低，沿着前车天线底端向上，速度又逐渐增大，并且在天线上方成涡团，在天线的左最高点达到最大值，随后，沿着左前点向后，速度又降了下来，并逐渐趋于平稳，中间车体的流场速度几乎相同，处于平稳状态，在接近尾车天线的时候速度又开始发生变化，尾车天线底部流场速度受到天线的阻挡速度达到最小值，尾车天线的最高点也是流场速度的最大值，形成涡团，从尾车天线往下开始，速度逐步下降，尾车的车头速度几乎降到了最低值。在列车的尾部都有一个尺寸大小差不多大的尾流。之所以在天线处，流场的速度有一个由降低-升高-降低的变化，是因为天线处产生的突起，阻挡了流场的运动方向，进而影响了流场的速度。不同车速情况下，头车天线的涡团大小是有差异的，车速越高，形成的涡团越大，速度变化越大。

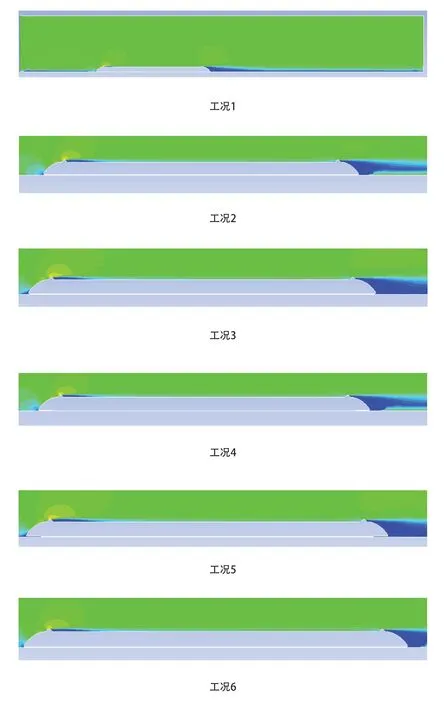
图3 工况1～6流场云图

对比相同车速情况下，静止地面与非静止的云图情况，在列车最前端，移动地面的列车是一个类似于涡流的流场，而静止地面产生的流场则没有，而是随着高度的增加速度层层增大的云图形状。

对比工况2跟工况4，工况6三种移动地面、不同风速下的流场云图，车体底部的流场分析，随着车速的提高，车体底部的流场速度变化越明显，越接近车体底部，流场的速度越低，最近处的流场速度几乎为零。

3.2 阻力系数分析

对比六种不同工况下，分析列车的阻力系数，得到如图4所示的测量数据，实验结果表明：

1）在考虑移动地面的情况下，消除地面边界层影响后，相同风速情况下，列车的总阻力系数增大。

2）无论是何种地面情况，头车的阻力系数都为负值，而车体、尾车、天线的阻力系数都为正数。

3）对比工况2、工况4、工况6，在移动地面的情况下，整车的总阻力系数随着车速的增大而降低。对比工况1、工况3、工况5，在静止地面的情况下，整车的阻力系也数随着风速的增大而降低。

4）在静止地面的情况下，不同风速的车头阻力系数几乎没有变化。移动地面的车头在不同风速下，车头阻力系数也没有什么变化。因此，车头的阻力系数并不随着速度的改变改变。但在同速度的情况下，车头的阻力系数会因地面是静止或者移动的情况而改变，移动地面情况，车头阻力系数会减小。

5）相同速度情况下，移动地面上的车体、尾车、天线的阻力系数跟静止地面相比较，都是变大的过程，只有车头的阻力系数是一个降低的过程，并且尾车的阻力系数占比最大，因此影响整车阻力系数大小的关键在尾车。

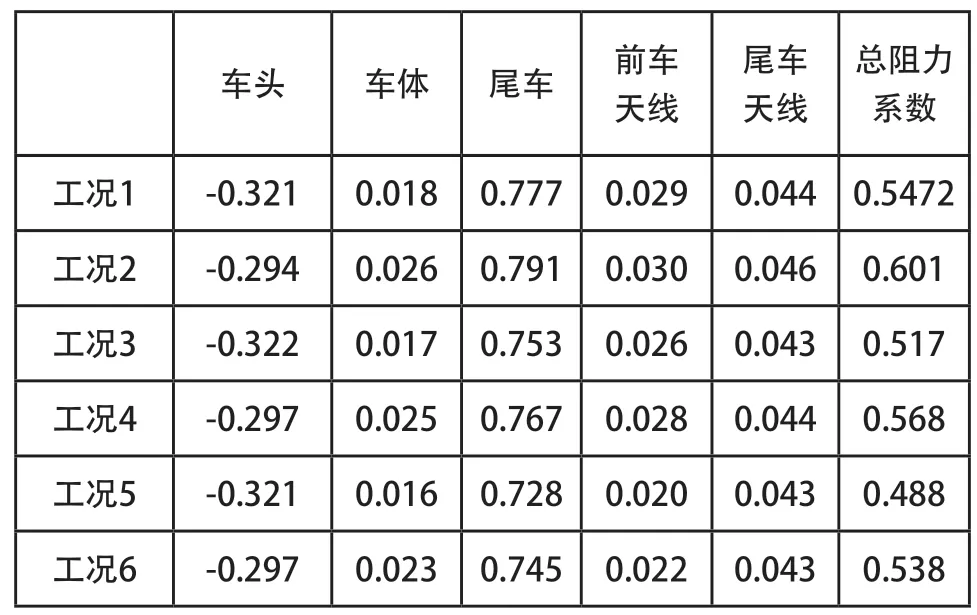
表2 阻力系数图

3.3 压力系数分析

图4 工况1压力云图

图5 工况2压力云图

各种工况下的压力云图相似，所以我们要对整车进行压力分析就要通过选取检测点的方式，分析车体各监测点的静压力系数，首先要进行检测点的选取，如图为所选取的监测点。从云图可以看出，由于中间车体顶部的压力系数几乎没有变化，所以选点的时候主要选取在车头和车尾以及车体的下方，共选13个监测点。如图6所示。

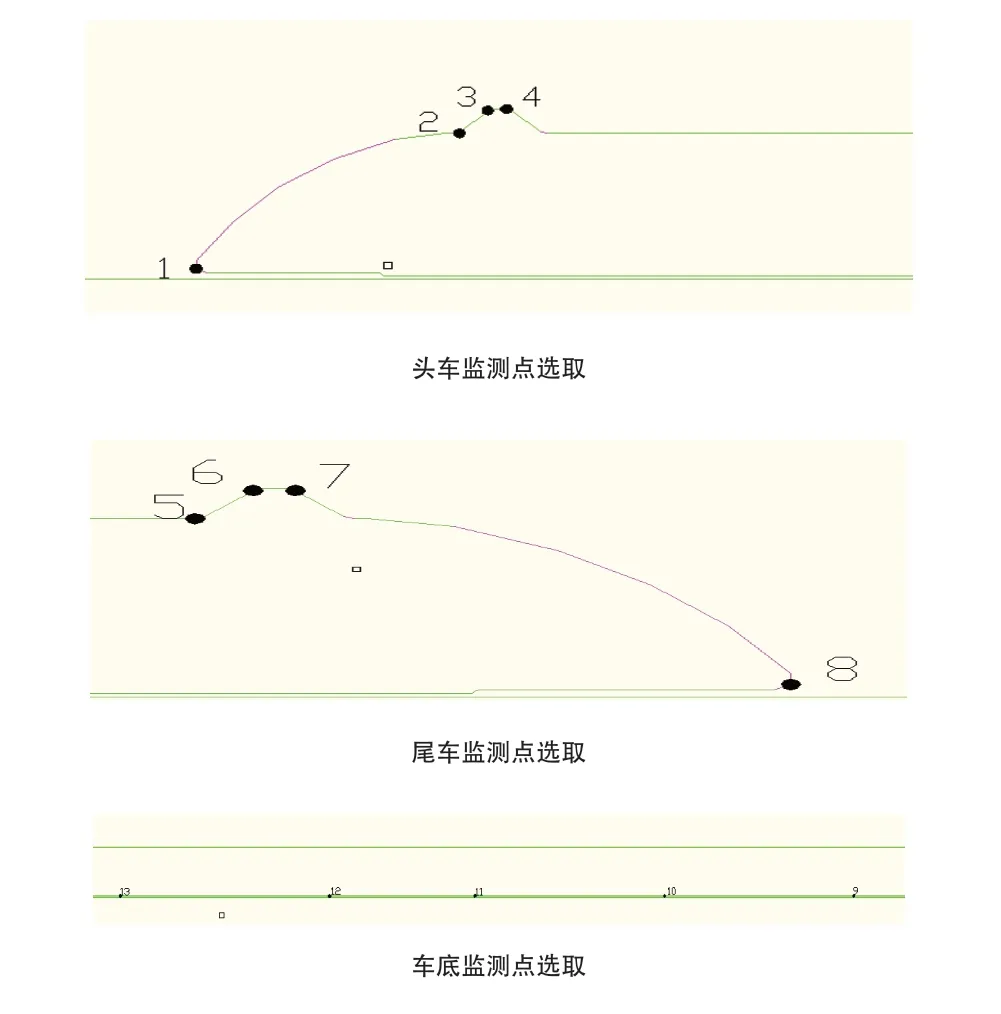
图6 监测点的选取

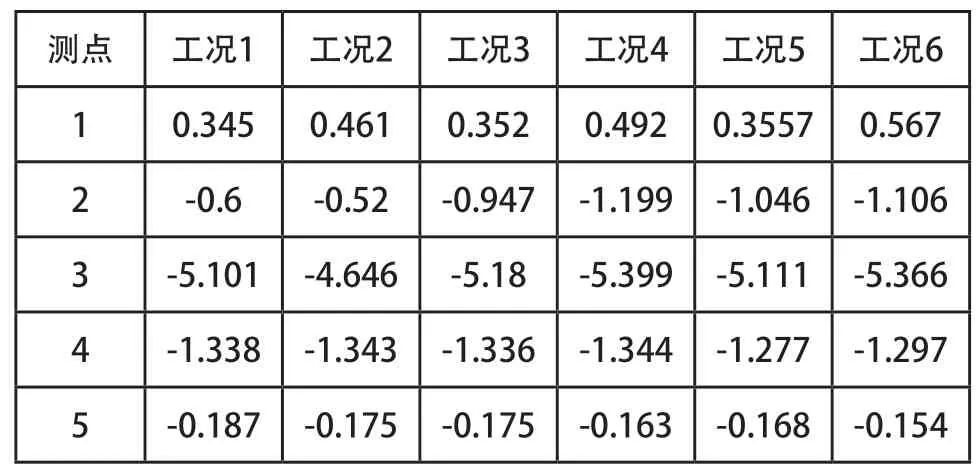
表3 监测点的压力系数表

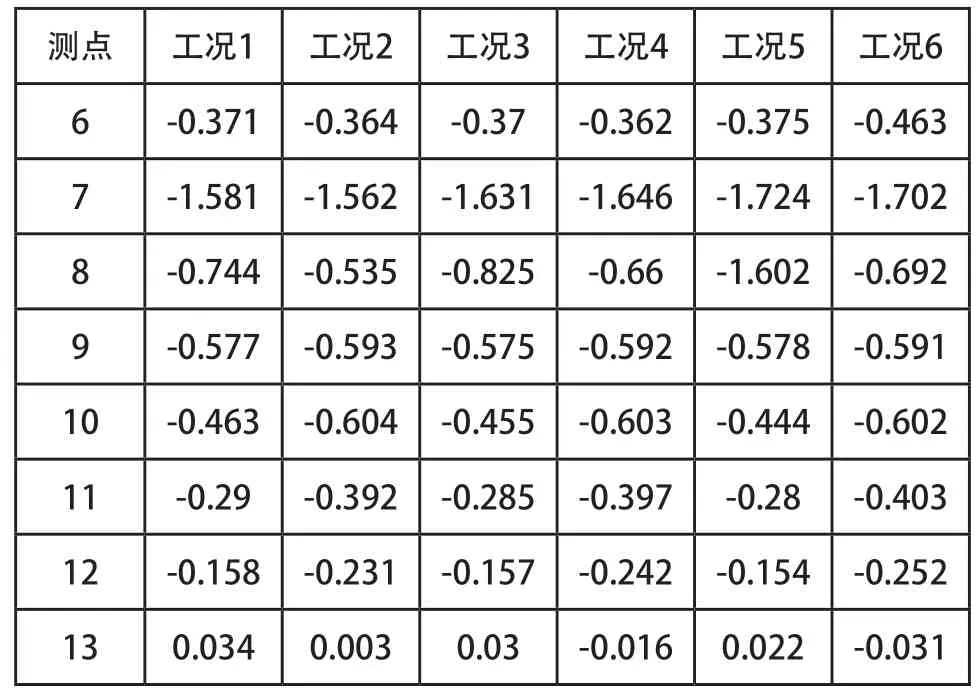
表3 （续）

对比不同工况下的云图和各监测点的压力系数可得到如下结论：

1）相同速度情况下，对比静止地面，在考虑移动地面消除地面边界层影响的情况下，在车头最前端，压力系数会变大，速度越大，这种效果越明显。

2）从压力云图可知，与静止地面相比较，采用移动地面后，对尾车头部的压力系数影响较大。压力系数都有减小，速度越大，这种变化越大。

3）与静止地面比较，考虑地面效应后，移动的地面使得车体底部的压力系数变化较大。在头车和尾车的车体底部，压力系数会变大，而在中车的车体底部，压力系数变大的更明显。

4）无论何种地面情况跟车速，车头的最大静压力系数产生在车头的最前点。

5）在都采用移动地面的情况下，列车顶部的压力系数变化不大，证明列车顶部压力系数与车速关系不大。

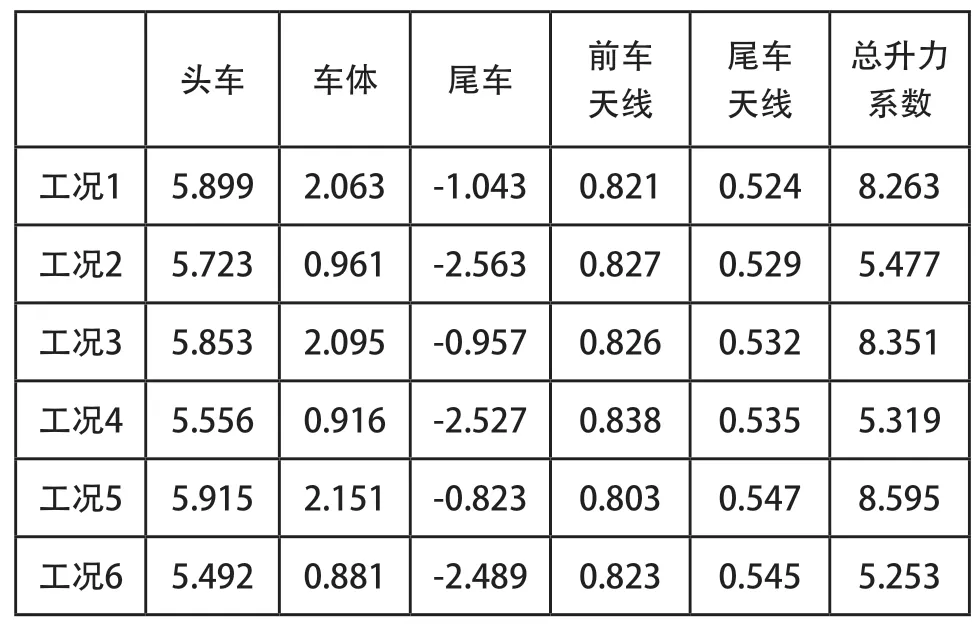
表4 升力系数图

3.4 升力系数分析

通过分析得出以下结论：

1）对比静止地面，在相同的车速情况下，移动地面使得磁悬浮列车的总升力系数降低。

2）头车的升力系数在整车的总升力系数中所占比例最大，对整车升力系数影响最大的是头车的升力系数。

3）尾车的升力系数为负数，其他部分的升力系数为正值。

4）对比工况1和工况2、工况3与工况4、工况5和工况6，移动地面使得头车、尾车、车体的升力系数都降低。

5）采用静止地面的情况下，升力系数随着车速的提高而变大。

6）采用移动地面的情况下，升力系数随着车速的提高而变小。

4 结语

通过研究表明：地面效应对高速列车的影响是显而易见的，如果不考虑地面效应，会对通过风洞实验来分析列车的气动力问题产生不可忽视的误差影响，本试验通过数值模拟的方法来验证地面效应对高速列车的气动力影响，并且分析出了结果，对以后关于地面效应对磁悬浮列车的影响研究起到了参考作用。本试验也存在缺点与不足之处，为方便后人查阅，将需改进的地方列出：

1）模型进行了大量的简化，车体底部的复杂结构并没有很好的表现出来；本试验应用的是二维模型，并没有使用三维模型很好的模拟整车的情况，造成了对数据测试的局限性。

2）受限于计算机的分析能力，在划分网格的时候，网格的总数有限，这就影响了计算的精度，尤其是车体底部的流场求解过程，所以计算精度还有提高的空间。

3）参考别的文献，此类型的试验都需要对比数据来验证分析数据的准确性，对此类型的试验验证方法最多的就是采用风洞实验的方法，但受限于试验条件，本试验并没有采用风洞实验来进行实际验证，而是以计算分析为主。验证结果的准确性，是通过跟高校合作，根据高校的风洞实验室的实际测量数值进行比对验证，保证了测量数据的准确性。