模糊减法聚类下大型机组设备故障自动化诊断方法

徐岳清，陈 旗

（1.无锡机电高等职业技术学校，无锡 214028；2.无锡汽车工程高等职业技术学校，无锡 214153）

0 引言

随着设备复杂性不断提高，工业生产对大型机组设备的故障诊断有了更高的要求，设备的高度复杂性使得故障诊断涉及了很多个部门的协同参与。大型机组设备故障的发生，会造成大量经济损失[1]。因此，对机组设备进行稳定安全的维护，已经成为了现代企业管理重要目标之一。

大型机组设备自动化水平快速提高，设备构成的复杂度也逐渐增大，这导致设备故障经常发生。而设备故障的表现形式也是各种各样的。一个设备的故障源有可能导致其他故障的发生，该特点给系统故障的诊断造成了很多困难。由此，找到适合的故障诊断方法，是该领域重要的研究方向。

大型机组设备故障具有多样性、突发性等特点，该特点使设备故障诊断成为了异常复杂的系统工程。互相独立的设备故障诊断系统，断然不能够适用实际的设备故障诊断，尤其是分布式的大型机组设备，上述特点导致大型机组设备故障诊断成为了亟待解决的问题。

文献[2]提出一种基于信息源聚类的故障诊断方法。该方法根据广泛收集大型机组设备故障资料，将其各种监测数据与故障征兆进行综合，得到比较全面的设备故障集与征兆集，通过对数据统计分析得到各个故障类型以及条件概率。然后在贝叶斯网络中建立故障诊断模型，利用设备故障诊断特点对贝叶斯网络推理过程进行改进，计算故障类型概率信息，通过概率信息对故障进行分类。该方法虽然简单，但是诊断精度低。文献[3]提出了基于二叉树的故障诊断方法。该方法在设计故障树结构的基础上，将基带信号作为输入信息，结合故障树最小割集、模糊故障树概率对故障树展开分析，根据输出结果完成故障诊断。该方法对诊断用时较短，但其诊断偏差较大。文献[4]利用EEMD分解结果对设备故障进行诊断，在分解设备振动信号的基础上重组信号，以此来减轻噪声信息对诊断结果的影响，然后分析信号的全息谱及其形态特征，也就是设备在各阶倍频下旋转的方向、形状、大小和各阶倍频间的关系等信息，从而反映设备振动的形态特征，以此特征为依据，形成故障诊断模型。该方法具有一定的实际意义，但是运行过程较为复杂。

针对上述传统方法存在的不足，本研究设计了模糊减法聚类下大型机组设备故障自动化诊断方法。

1 故障自动化诊断方法设计

1.1 大型机组设备故障特征量自动化提取

为提高大型机组设备故障诊断的准确性，需要对机组设备的特征量展开自动化提取。

针对大型机组设备的特殊性，本文利用多维模糊贴近度实现设备故障特征量的自动化提取。

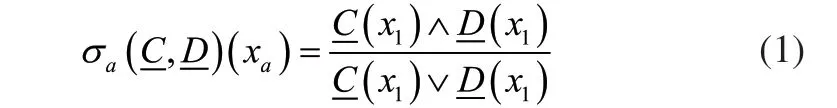
式(2)可以比较详细地描述出故障信号与正常信号间综合相似度的模糊贴近度。在上式求解过程中选择是任意的，的选择也任意，只要与结合后，满足模糊贴近度定义就可以。因此，本文针对不同系统以及具体工作情况，对选择的进行调整，将多维模糊帖近度可以与实际的实现中最好的信号匹配。

获得故障信号与正常信号间最不相似的程度以及分布，这样可以得知和正常信号比较，设备的故障信号变化的最大值。把的各系数x1,x2,…,xn进行统一形成简单的系数函数，就是N 维的函数转换成，变为一维函数：

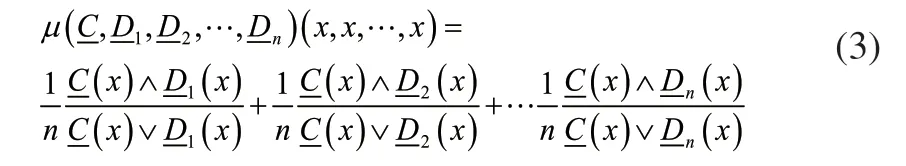
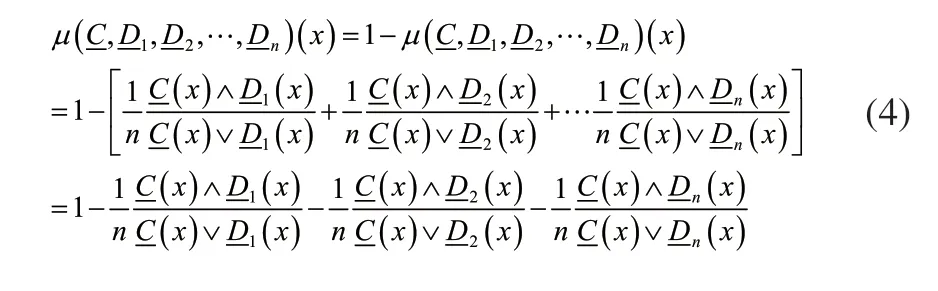
式(4)结果中包含故障模糊的隶属函数确立中比较重要的砝码。

根据模糊集λ的水平贴近域有：

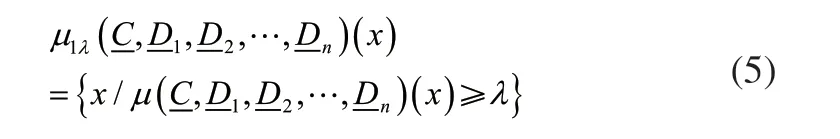
经上式就能够知道设备故障信号的变化大于某个程度的点，则λ被称为筛选因子。λ的取值可以根据机组设备的具体运行情况来确定。

对各故障信号的样本间多维模糊贴近度进行计算，这样就可以得到设备故障信号间的最相似点。假设影响E集间多维模糊贴近度内各因素为“模糊贴近度”式中：

式(7) 能够描述在设备发生故障的状况下，被检样本间的整体相似贴近度。在结合之后满足模糊贴近度的定义就可以。因此本文针对不同系统与具体情况，对选取的进行调整，可以使模糊贴近度各系数统一变成单系数函数，就是将N维函数变为一维函数

在此基础上，根据故障隶属函数h(z)确定故障的特征参量。对上面求得的被检样本间整体相似度的多维模糊贴近度，引入噪声与特征频率点影响，并选择信号间的整体相似度函数，由此获得符合设备故障的模糊隶属函数如下：

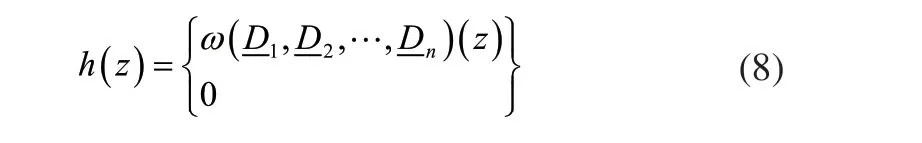
1.2 大型机组设备故障自动诊断

在工业化技术不断发展的同时，大型机组设备的故障也呈现出一些新的特征。当设备发生故障时，常常会连带各种故障同时发生。则要想在比较复杂的设备系统中实现故障的快速诊断，仅凭理论信息会出现故障漏报或虚报现象。为此，本研究结合D-S证据理论对设备故障进行准确诊断。

1.2.1 D-S证据理论概念与设备故障

针对本文研究的大型机组设备故障诊断过程，采用D-S证据理论将所有可能出现的设备故障类型建立成一个集合，该集合实质就是一个识别框架，利用D-S证据识别框架Ω中机组任何一种设备故障类型对应的类别特征被称为证据。

假设给定了一个大型机组设备故障诊断识别框架Θ，其中包含了全部可能的设备故障类别。则基本概率赋值函数m（A）可描述成该函数满足下面的两个条件：

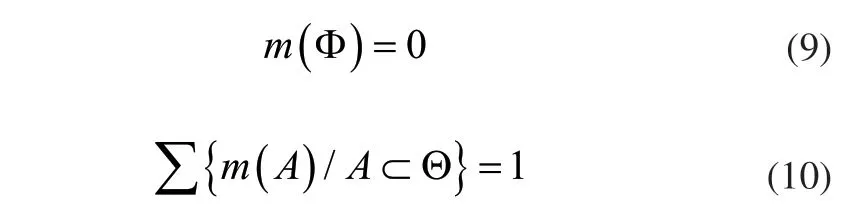
大型机组设备故障的自动化诊断过程中，将不同阶段的机组设备运行状态的故障发生概率分布定义为故障基本概率赋值函数，m（F）可描述为设备故障诊断相关人员对某种设备故障F定义的关于该类型设备故障评价指标值。m（A）常常被看作是某个命题的质量函数，或是mass函数，经过安装在大型机组设备中的传感器获得的实验数据构造成的。

本文融合于D-S证据理论实现大型机组设备故障诊断的主要思想是：将获取的大型机组设备故障诊断证据划分为不同且相互独立的部分，根据这些大型机组设备故障诊断证据完成识别框架判断。将各识别框架内每个假设对应的大型机组设备故障诊断证据判断数据，将其称为该证据下的置信函数，其相应的概率分布可描述为置信函数的基本分配系数，针对某个诊断类型假设，根据特定合成规则，实现不同设备故障诊断证据置信函数的汇总，由此获得机组设备故障诊断综合证据下的假设总信任度。

针对给定的识别框架Θ，该框架中利用概率赋值函数得到的置信函数为：

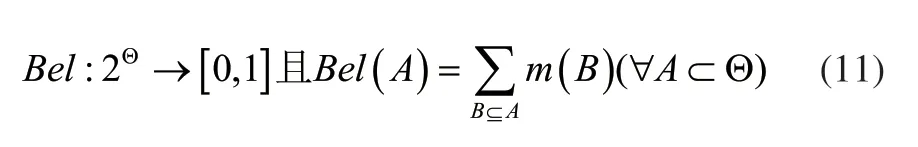
其中，Bel（A）表示对A总的置信程度，通过上式可知，Bel（A）为A中全体子集可能性度量和，由此可以得到互斥命题：

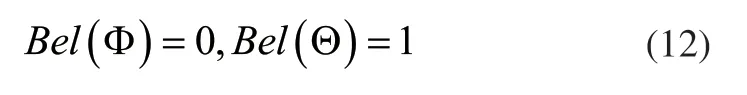
结合叠加原理对式(12)进行描述，结果如下：

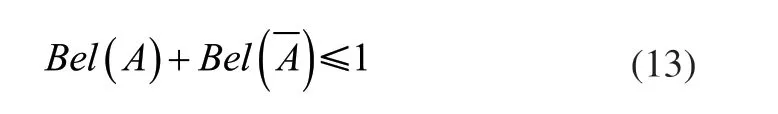
此外，假设m（A）>0，那么称A是置信函数Bel焦元，全部的焦元被称为它的核。

1.2.2 D-S证据组合规则及大型机组设备故障诊断

对于采用D-S证据理论对大型机组设备故障诊断全部证据集合内的数值毫无关联的子集进行判断，根据Dempster组合规则将不同类型的设备故障诊断证据相应的置信函数进行组合。其中，Dempster组合规则为：

假设Bel1与Bel2处于相同的证据识别框架中，Bel1与Bel2的概率函数分别为m1、m2，焦元依次为A1,A2…Ak与B1,B2…Bl，若式(14)成立：

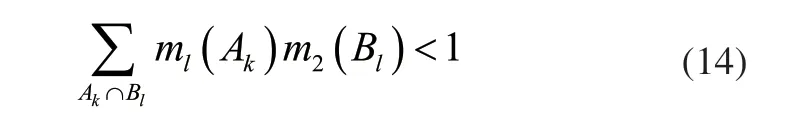
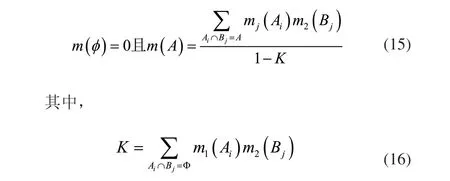
2 实验与分析

为验证上述设计的模糊减法聚类下大型机组设备故障自动化诊断方法的整体性能，设计如下实验。

在Paxos环境下搭建实验平台。实验数据取自于山东大棚膜机组设备，分别利用本文方法和文献[2～4]方法对实验对象的故障展开自动化诊断实验，并对比不同方法的可实践性。

图1所示为不同方法故障诊断时间对比结果。

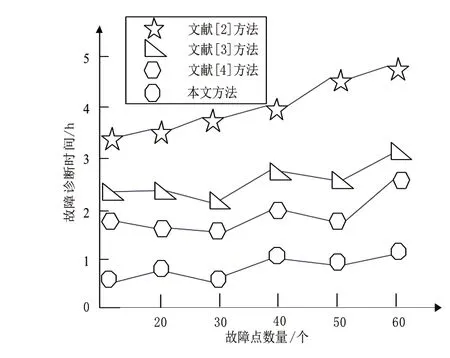
图1 不同方法故障诊断用时对比

图2所示为不同方法的诊断正确率对比结果。诊断正确率可通过式(17)获得：

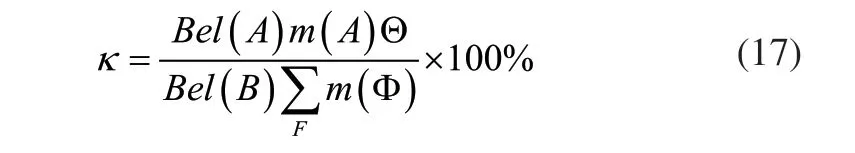
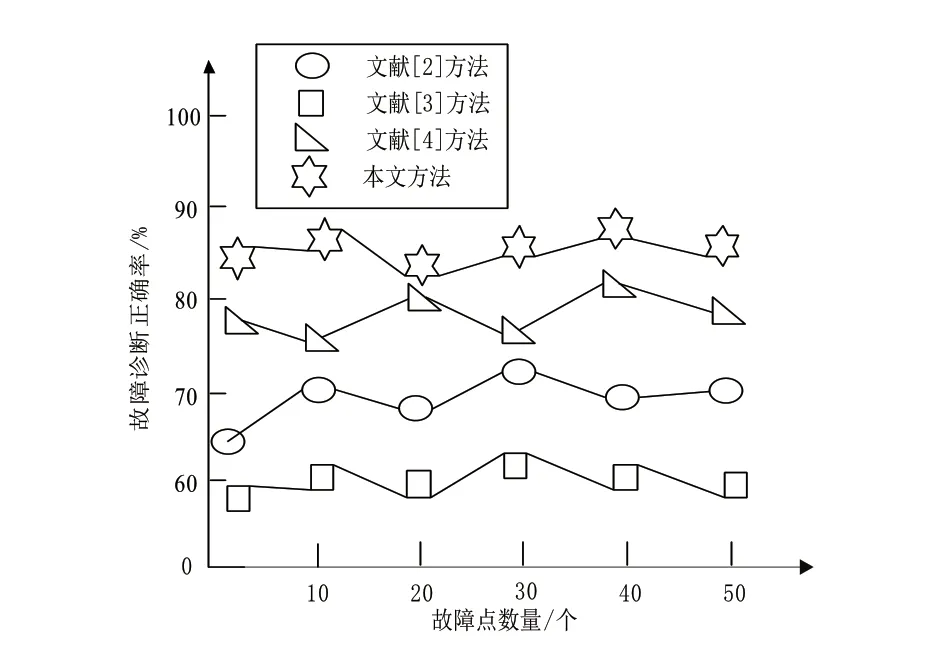
图2 不同方法故障自动化诊断正确率对比

图3所示为不同方法故障特征量提取时间对比结果。

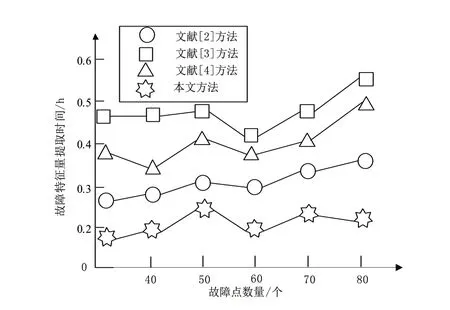
图3 不同方法故障特征量自动提取时间对比

图4所示为不同故障诊断方法对设备正常运行信号频率造成的影响的对比结果。

图4 不同故障诊断方法对设备正常运行信号频率的影响对比

综合分析上述实验结果可知，文献[2]方法利用大型机组设备故障诊断特点对贝叶斯网络推理过程进行改进，计算故障类型概率信息，通过概率信息对故障进行分类，故障特征不明确，分类精度低，导致故障诊断的效率偏低；文献[3]方法根据二叉树结构及其原理，以基带信号为对象构建二叉树，未考虑到大型机组设备的复杂性与多分解性，使故障诊断的效率低、诊断结果有误差；文献[4]方法根据二维全息谱，能够获得设备在各阶倍频下旋转的方向、形状、大小和各阶倍频间等信息，从而反映设备振动的形态特征，以此特征为依据，形成故障诊断模型。该方法仅仅利用单一的形态特征形成故障诊断模型，导致故障诊断正确率偏低；本文方法利用多维模糊贴近度实现设备故障特征量提取，并利用D-S证据理论完成模糊减法聚类下大型机组设备故障的有效诊断。

实验证明，本文设计的模糊减法聚类下大型机组设备故障自动化诊断方法可以快速可靠地对模糊减法聚类下大型机组设备故障进行诊断，为保障机组设备的平稳运行奠定了基础。

3 结语

采用当前方法诊断大型机组设备故障时，存在诊断误差大等问题，为此，本研究设计了模糊减法聚类下大型机组设备故障自动化诊断方法。在完成方法设计后，本研究还利用仿真对比实验验证了该方法具有诊断效率高、准确率高的优点，充分证明了其可行性。