基于孪生支持向量回归的风力机功率预测方法

郭玉立，文泽军

（湖南科技大学 机械设备健康维护湖南省重点实验室，湘潭 411201）

0 引言

开发利用清洁无污染的风能是当今趋势所在。风电场往往选址在环境复杂多变的高海拔区域，受环境的不确定性因素影响导致风力机产能低下甚至事故频发。分析影响风力机性能的不确定性因素并依据短期历史运行数据实现功率的精准预测对风力机状态预警具有重要意义。

国内外学者围绕风力机运行状态的不确定性进行了大量研究：Jordan等[1]采用人工网格机器学习方法，将风切作为输入参数进行风电机月发电量的预测；张帆等[2]提出一种基于SCADA参数关系的风电机组运行状态识别方法，采用时间滑动窗口模型进行输入输出参数的多项式回归拟合进行风力机运行状态识别；梁颖等[3]利用数据挖掘技术考虑风电机组各部分与子系统之间的相互作用与耦合关系，建立风电机组整体运行状态的评估模型；谢研等[4]利用MATLAB对测风数据进行拟合并验证了ZephlrLider实时监测数据的实效性；Tinghui等[5]将风向数据转换成正弦值和余弦值时间序列参数，提出一种风力机偏航范围最大风能的提取；Luis等[6]利用神经网格建立监测系统进行风力机疲劳载荷预测用于成本效益的替代方案；Yu等[7]提出一种描述时空变化过程特性的时空特征，将风力机采集的数据映射到飞机上根据相对位置行测场景图并通过深卷积网格应用于风力机发电量的预测；肖桂雨等[8]利用风力机SCADA数据提出一种基于小波分析和神经网格的智能算法通过分析风力机故障信号的特性，从而实现风力机故障诊断与预测；Fouzi等[9]采用决策树的套袋方法进行风力机发电量预测，此方法具有合并多个模型减少总体误差的优点；张毅等[10]提出了基于灰色模型的风电功率预测方法，适用于风电系统在线预测；张滕等[11]通过我国西北地区某风场近三年风机失效情况采用贝叶斯估计建立大型风电机可靠性变化模型。以上研究主要是依据风力机SCADA数据的实时运行数据进行在线状态识别；依据风电场历史故障数据采用概率统计的方法进行故障率分析与预测。在采用机器学习的方法分析风力机主要输入因素、基于风力机SCADA系统的历史小样本数据实现功率的精准预测方面有待进一步研究。

针对以上不足，本文提出一种基于孪生支持向量回归的风力机功率预测方法。首先在孪生支持向量回归中分别采用线性核函数与多项式核函数建立预测模型，参数寻优上采用遗传算法，并以平均预测精度作为评价指标；基于SCADA数据分析了风力机运行环境的不确定性并确定影响其运行状态的输入因素，分析风力机工作原理进行数据预处理并选取能够直观的表示风力机性能的输出因素；以2MW风力机为研究对象分别采用线性核函数与多项式核函数孪生支持向量回归方法进行功率预测。通过比较平均预测精度得出多项式核函数孪生支持向量回归预测方法的预测精度较高。实现了依据风力机SCADA系统中历史小样本数据对功率的精准预测，对风力机运行状态预警方面具有重要作用。

1 风力机功率预测模型

1.1 孪生支持向量回归方法

孪生支持向量回归是在孪生支持向量机的基础上提出的。孪生支持向量机基本思想是在两类别中产生两个不平行的超平面，使得每一个超平面尽可能地接近两类中的一个，并尽可能地远离另一类；Peng[12]在孪生支持向量机的基础上提出将两个不平行的超平面进行分类并构建一对不敏感的上下界函数，使得每个界函数求解过程中计算量大大减小。该方法不仅计算速度快，且具有良好的泛化性。

将风力机的输入与输出分别定义为x和y，则样本集可表示为：（x1，y1），…，（x1，y1），假设样本是一个n维向量，样本数为l，将输入定义为矩阵A=[x1，…xl]T，输出为Y=[y1，…yl]T；向量e=[1，…，1]T为适应样本维度的单位向量。其表达式为：

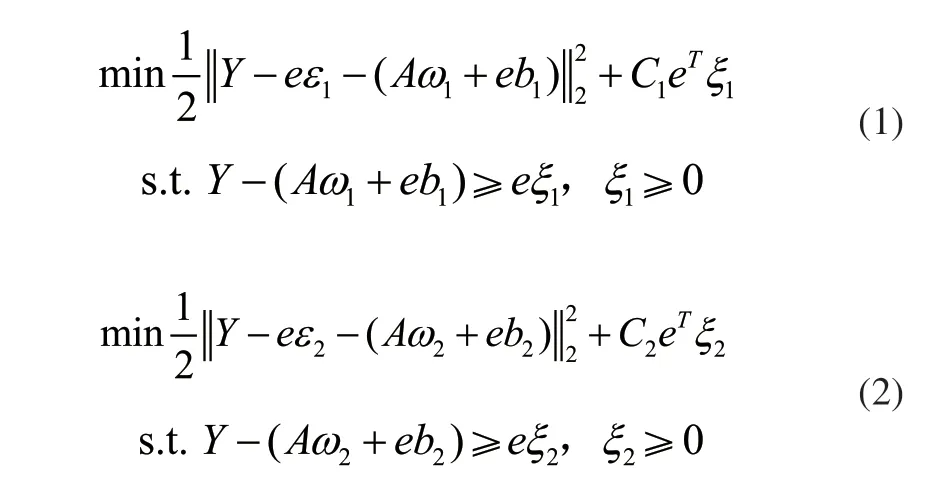
其中：C1，C2是影响因子，ε1，ε2是参数；C1，C2≥0；ε1，ε2≥0；ξ,η是松弛变量。

考虑到样本可能存在非线性关系，将K定义为非线性核函数，令K（A，AT）是维数为l的核矩阵，其中第（i，j）个元素（i，j=1，2，…l）为式(3)所示。

1.2 线性核函数与多项式核函数

核函数有线性核函数和多项式核函数表达式分别为式(4)与式(5)：

其中：α>0，c>0，d∈N。

利用拉格朗日函数KKT约束条件，将式(1)与式(2)转化为对偶关系如式(6)和式(7)所示[12]：

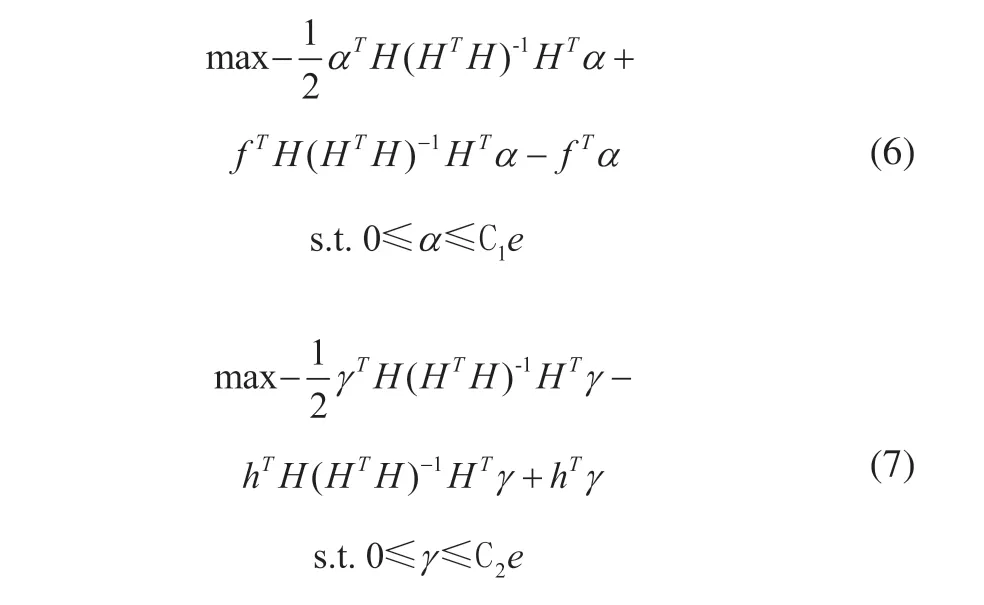
其中：H=[K（A，AT），e]；f=Y-ε1e；h=Y+ε2e。经计算得式(8)和式(9)：

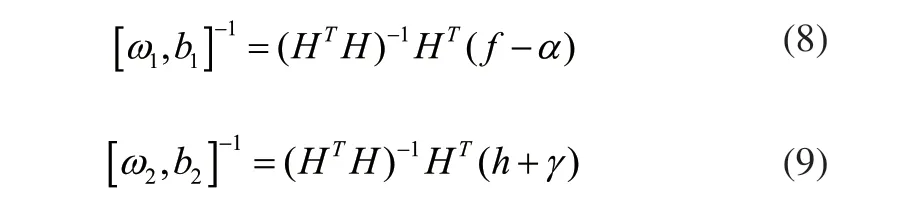
构建风力机输入的回归函数如式(10)所示：

1.3 参数寻优

孪生支持向量回归方法中核函数参数寻优上可利用遗传算法来解决。

遗传算法是模仿自然界生物进化和遗传机制发展起来的随机全局搜索方法，并自适应得控制搜索过程并提供最优的解决方案，首先从目标问题的可能潜在解集的一个种群开始，通过选择、交叉和相互变异产生新的具有代表解的种群[12]。调取R语言中的GA（Genetic Algorithm）包，设置种群数目为50，迭代次数为100，选取均方差作为迭代过程中的适应度值。

1.4 评价指标

风力机功率作为预测模型的输出因素。分析孪生支持向量回归方法的预测功率值与实际功率值的偏差，偏差量占实际功率的比重为预测功率的偏差率。将平均预测精度作为评价两种预测方法精准度的指标。如式(11)所示：

式中，M为预测功率的平均精度；yt为风力机实际功率值，为预测功率值，N是预测样本总数。

2 实例验证

2.1 风力机SCADA数据预处理

风力机的工作原理是通过捕获的风能促使叶轮的旋转，由旋转的机械能转化为电能的能量转换过程。本文采取的研究对象是我国南方某风电场2MW直驱式风力机。风力机SCADA数据是通过设置在风力机各个重要部位上的传感器进行在线监测并数据储存的系统。数据记录周期从1s～n min，本文采取的SCADA数据是我国南方某风电场秒级记录的10min内的平均值。风力机SCADA数据记录的主要参数有：风速、风向、功率、主轴温度、轮毂转矩、机舱温度等。

风力机的自由状态是指完全不受人为控制的工作状态。停机状态是因风力机所处的环境条件不适合工作或其他原因引起的停机；风力机限功率状态分两种：1）由于电力系统储存接近饱满不能够接纳风力机产生的电能；2）风力机的最高功率为2000W。风力机SCADA数据中以下情况记录的数据应去除：

1）标准风速3m/s～22m/s以外；

2）停机、维修时的数据。

风力机的输入因素有风速、风向、环境温度共3个变量；输出为功率。选取风力机SCADA系统连续记录的500组数据，采用机器学习的方法训练前300组数据，依据后200组数据的输入并预测其输出。预测时将输入作为影响因素，输出为功率。风力机SCADA数据预处理后选取的500组连续数据中时序-功率折线图如图1所示：

图1 数据筛选后的时序-功率折线图

归一化处理是机器学习常用的方法，可以提升计算结果的精度以及减少计算量加快计算速度。功率归一化如式(12)所示：

其中：yt为风力机功率实际值；ymax为功率最大值；yi为功率归一化值。归一化的风力机时序-功率折线图如图2所示。

图2 数据筛选后的时间-功率归一化折线图

2.2 结果分析

以R语言为计算工具，抓取风力机SCADA数据中输入因素：风速、风向和环境温度；输出为功率。调取GA包和Psoptim包分别采用遗传算法进行参数寻优。选取风力机预处理过的SCADA数据中500组数据，训练前300组预测后200组。预测结果如图3、图4所示。

图3 实际功率与线性核函数预测功率对比图

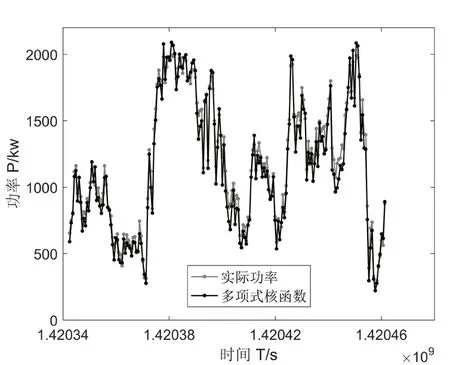
图4 实际功率与多项式核函数预测功率对比图

由此可知：多项式核函数孪生支持向量回归方法的预测功率折线与实际功率折线重合度较高，且线性核函数孪生支持向量回归方法的功率预测精准度与实际功率相比明显偏低。

图5 时间-线性核函数与多项式核函数预测功率偏差折线图

由图6、图7可知，随着环境温度与风速的增大，多项式核函数孪生支持向量回归方法预测功率值的偏差量相对于线性核函数孪生支持向量回归预测方法偏小且总体趋势较为稳定。

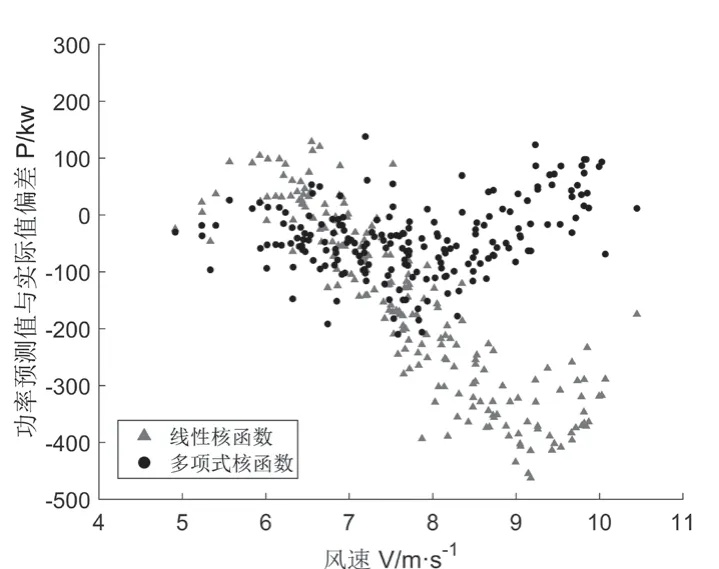
图6 风速-线性核函数、多项式核函数预测功率偏差散点图

图7 环境温度-线性核函数、多项式核函数预测功率偏差散点图

分别对比实际功率值与线性核函数、多项式核函数孪生支持向量回归的预测功率值，以平均预测精度作为评判预测功率精度高低的标准。图8为线性核函数与多项式核函数孪生支持向量回归预测方法的预测精度折线图；表1为两种预测方法的平均预测精度：

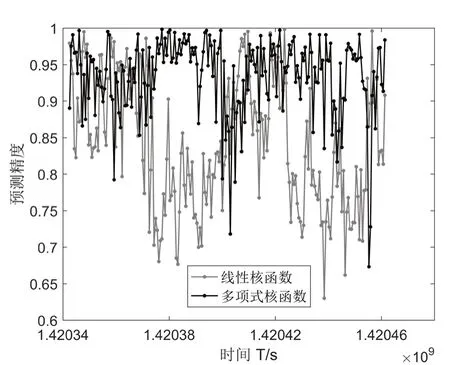
图8 线性核与多项式核预测精度折线图

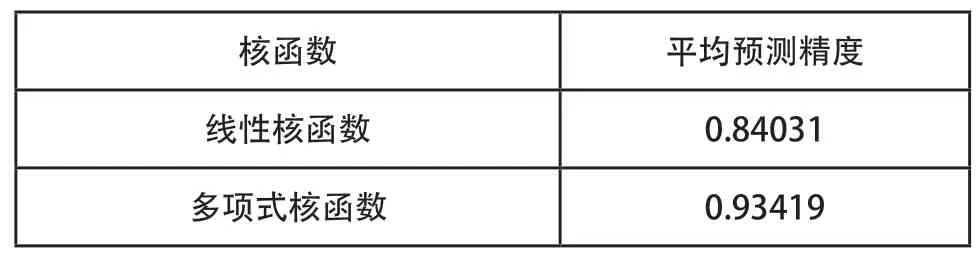
表1 线性核函数与多项式核函数预测精度

以上分析可以看出，线性核函数与多项式核函数孪生支持向量回归方法并运用遗传算法进行参数寻优对风力机功率预测的可行性。通过对比平均预测精度得出多项式核函数孪生支持向量回归预测方法的精准度较高。实现了依据风力机SCADA系统历史小样本数据对功率的精准预测。对风力机性能退化、状态预警等方面带来帮助。

3 结语

1）在孪生支持向量机的基础上选用孪生支持向量回归，分别采用线性核函数对多项式核函数孪生支持向量回归预测，参数寻优上运用遗传算法进行风力机功率预测。

2）分析风力机的性能特性与运行环境，选取SCADA数据中影响风力机运行状态的输入因素、能够直观的展现出风力机运行状态的输出因素。进行数据预处理并提取有效的连续数据。验证了基于孪生支持向量回归方法对风力机功率预测可行性，其中多项式核函数孪生支持向量回归方法预测精度较高。

3）提取风力机SCADA系统中历史小样本数据采用机器学习方法实现了对风力机功率的精准预测。将风电场气象信息作为输入因素可精准预测风力机的输出功率。对风力机状态预警、性能退化等方面具有重要意义。