基于目标应变分布的TC17合金双性能盘预成形形状优化设计

翟江波

基于目标应变分布的TC17合金双性能盘预成形形状优化设计

翟江波

（航空工业陕西宏远航空锻造有限责任公司，陕西 三原 713801）

研究TC17合金双性能盘目标应变分布下的预成形形状优化设计方法。采用拉丁超立方试验设计方法对预成形形状设计变量抽样选取样本点，并通过Deform有限元数值模拟获得样本设计变量下的局部应变分布。以局部应变分布与目标应变分布之间的方差最小为目标函数，采用Kriging方程建立近似替代模型预测响应应变误差，并结合遗传算法，以锻件的充填率及材料利用率为约束条件，优化设计预成形形状。近似替代模型预测的应变误差与基于有限元数值模拟计算获得的应变误差之间的最大相对误差和最小相对误差分别为10.8%和0.01%。这表明Kriging近似替代模型在预测响应应变误差时的精度较高，具有较好的可靠性，采用优化后的预成形形状经多道次等温锻造后的等效应变分布满足目标应变分布的设计要求。

TC17合金；Kriging模型；有限元数值模拟；遗传算法；优化设计

双性能结构实现了零件上不同部位力学性能的渐变，满足了零件不同部位对力学性能的不同要求，可显著提高零件在恶劣服役条件下的使用可靠性和使用寿命，因而，双性能盘在未来高推重比航空发动机新结构制造领域具有广阔的应用前景。TC17(Ti- 5Al-2Sn-2Zr-4Mo-4Cr)合金是一种富的(+)型两相钛合金，具有高强度、高韧性、高淬透性等优点，采用TC17合金研制双性能盘，通过控制塑性应变以实现对片层组织球化率的主动调控，以获得一侧为等轴细晶组织，另一侧为网篮组织，过渡区有序渐变的双重组织是获得双性能零件的有效途径[1—5]。

采用有限元数值模拟和优化技术相结合的方法实现模具和预成形形状的优化设计，是等温锻造时主动调控局部塑性应变的一个行之有效的方法。在过去的几十年，国内外许多学者广泛采用有限元数值模拟和优化技术对金属成形过程中的模具和预成形形状进行优化设计。Zhao等[6—7]采用有限元数值模拟与灵敏度分析相结合的方法，优化设计了预成形模具形状尺寸以控制变形的均匀性。Gao和Grandhi[8]以晶粒尺寸细小均匀为目标、以锻件的充填率及材料利用率为约束条件，采用灵敏度分析方法优化设计了非等温锻造过程中坯料的初始形状和模具速度。Sundararaghavan和Zabara[9]采用多尺度灵敏度分析方法优化设计了金属成形过程中的材料性能。Shao等[10—11]以锻件的材料利用率和变形均匀性为目标，采用Deform-3D有限元数值模拟和拓扑方法，优化设计了锻件的预成形形状。Chen等[12—13]采用任意拉格朗日欧拉公式和Kriging方程，并结合有限元数值模拟，优化了挤压模具结构。

尽管前期研究工作已经大量报道了关于金属成形过程中的微观组织预测[8,14]和预成形形状优化设计[15—17]，但是尚未报道关于等温锻造过程中基于目标应变分布的预成形形状优化设计方法。文中采用拉丁超立方试验设计、Kriging近似替代模型、Deform有限元数值模拟和遗传算法相结合的方法，研究了TC17合金双性能盘目标应变分布下的预成形形状优化设计方法，设计过程中坯料的形状参数被确定为设计变量，局部应变分布与目标应变分布之间的方差最小为目标函数，锻件的充填率及材料利用率为约束条件。

1 优化设计过程与方法

文中优化设计的目标是获得最优的预成形形状参数，通过采用优化后的预成形形状，使钛合金盘件等温锻造后其形状尺寸精度满足要求，且盘件的应变分布满足设计要求，以实现片层组织球化率的主动调控。

1.1 选择设计变量

文中预成形形状主要由6个形状参数R(=1,...,6)来决定，图1是优化设计前的预成形形状。为了便于预成形形状参数的优化设计，选择了5个设计变量(,Y1,X2,X3,X4)用于描述预成形形状的6个形状参数，这5个设计变量的取值范围如表1所示。

图1 预成形件的初始形状

表1 设计变量的取值范围

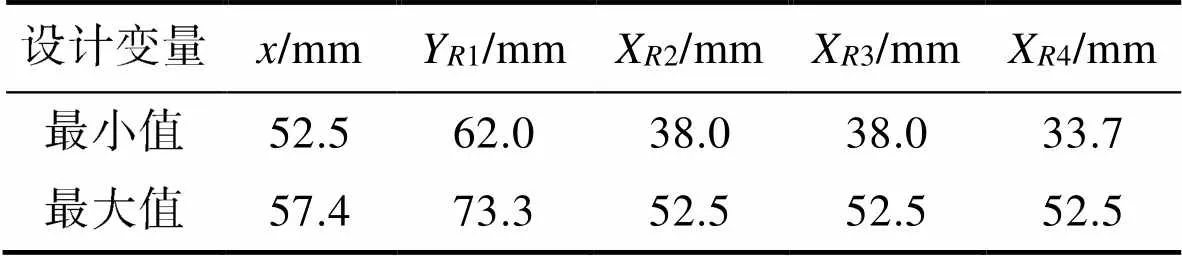
Tab.1 Range of design variables

1.2 建立目标函数

图2为应变对片层组织TC17合金高温变形时和变形后热处理时的球化行为影响。对比图2a和图2b可以看出，当变形程度由30%提高到70%时，TC17合金在850 ℃变形时，其针状组织部分转变为细小的等轴组织，部分片层发生扭折或破碎，形成长度与厚度比值较小的条状，通过定量分析表明，片层组织的球化率由0.7%提高到5%，这主要是因为，随着变形程度的增加，塑性变形过程中较大的应变促使片层相晶粒内部积累了大量的位错[18]，位错通过滑移和攀移形成亚晶界，随着变形的继续进行，相沿着亚晶界楔入片层相最终导致了片层相分离破碎，促使了片层相的动态球化。对变形温度为850 ℃、变形程度为30%的TC17合金压缩试样在820 ℃保温1 h，其片层相的球化率提高到37%，如图2c所示。由图2d可以看出，对变形温度850 ℃、变形程度70%的TC17合金压缩试样在820 ℃保温1 h后，TC17合金的微观组织主要由等轴相和基体组成，其中微观组织中有少量的短棒状相。片层相的球化率由37%提高到了66%。根据以上试验结果表明，TC17合金双性能盘上不同区域的应变分布对球化率的影响显著，因此，为了获得有序渐变的双重组织，有必要有效控制TC17合金双性能盘等温锻造过程中的局部应变分布。

图2 应变对片层组织TC17合金球化行为的影响

为了较好地描述采用Deform有限元数值模拟系统计算获得样本设计变量下的局部应变分布，文中在TC17合金盘上均匀选取了75个特征点，其特征点的分布如图3所示。最终以样本设计变量下有限元数值模拟系统计算获得的局部应变分布与目标应变分布之间的方差最小为目标函数，其目标函数表示为：

图3 预锻件特征点的分布

式中：为预锻件的特征点数量（=75）；ε,calculated为Deform有限元数值模拟系统计算获得的局部应变分布；ε,desired为目标应变分布。

1.3 确定约束条件

金属在锻造成形过程中，首先应确保锻件能完全充模，获得符合设计要求的精确外形；其次应尽量减小锻件毛边体积，避免造成材料浪费，因此，在进行预成形形状优化设计时，文中将锻件的充填性与材料利用率同时作为优化问题的约束条件，两个约束条件分别表示为[8]：

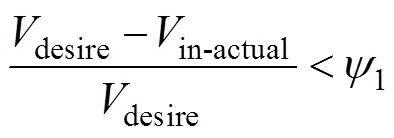
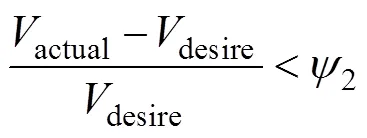
式中：desire是理想状态的充满模腔的材料体积；in-actual是模腔内部实际充填情况下的材料体积；actual是终锻后带有毛边的总锻件材料的实际体积；1和2分别用于描述与锻件的充填性与材料利用率相关的约束条件。

1.4 Kriging近似替代模型

以近似模型替代计算机分析程序进行优化设计可以提高计算效率，为实现预成形形状的快速优化设计提供了一种可行的方法。基于有限元数值模拟结果，建立准确、高效的近似替代模型是实现上述优化设计方法的关键，文中选用Kriging方法建立设计变量与目标函数的近似替代模型。Kriging方程是一种统计学插值模型[19]，该方程最早由南非地质学家Krige提出[20]，由于该方程对非线性函数的良好近似能力和独特的误差估计功能，正受到越来越多的研究者的关注[21—22]。

遗传算法是一种通过模拟自然进化过程搜索最优解的方法[23]。文中采用一种Kriging方程为基础的遗传算法优化TC17合金双性能盘等温锻造过程中的预成形形状，Kriging方程表示为[22]：

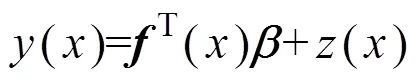
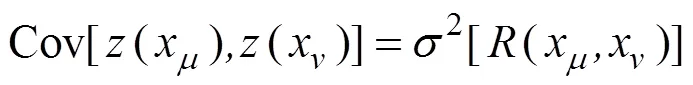
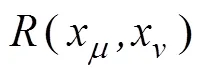
最终Kriging方程表示为：

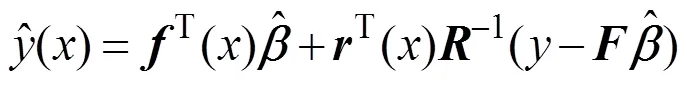
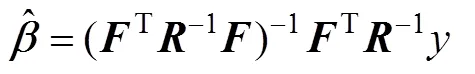
式中：为基函数()在某个试验点下的一个向量。空间相关矩阵表示为：

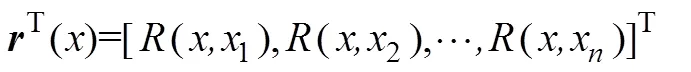
方差2的最大似然估计为：

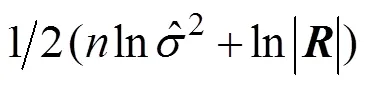
2 优化设计结果与讨论

建立应变误差Kriging近似替代模型时，需要选取设计变量取样本点，并通过Deform有限元数值模拟获得这些样本点对应的应变误差响应值。文中采用拉丁超立方试验设计方法对预成形形状设计变量进行抽样。这种抽样方法属于空间填充试验设计方法，能够保证样本点尽可能均匀地分布在整个设计变量空间内，同时能避免重复点的出现。通过抽样获得81组样本点用于建立应变误差Kriging近似替代模型，然后采用遗传算法优化Kriging近似替代模型中的参数，表2为抽样获得的81组设计变量样本点及对应的样本点下采用Deform有限元数值模拟计算获得的响应应变误差。

图4为预成形形状优化的流程。首先确定预成形形状优化设计变量及取值范围，通过Deform有限元数值模拟计算获得样本设计变量下的局部应变分布，再采用拉丁超立方试验设计方法对预成形形状设计变量进行抽样选取样本点，并以局部应变分布与目标应变分布之间的方差最小为目标函数，然后采用Kriging方程建立近似替代模型预测响应应变误差，并结合遗传算法，以锻件的充填率及材料利用率为约束条件，优化设计预成形形状。

图5为Kriging近似替代模型预测的应变误差与基于有限元数值模拟计算获得的应变误差之间的比较。可以看出，基于Kriging模型预测的响应应变误差与基于有限元数值模拟计算获得的应变误差之间的最大相对误差和最小相对误差分别为10.8%和0.01%，这表明Kriging近似替代模型在预测应变误差时的精度较高，具有较好的可靠性。优化后的设计变量,R1,R2,R3,R4分别为56.0，65.0，39.2，40.0，41.7 mm。图6为优化设计后的TC17合金双性能盘预成形形状及多道次等温锻造后的等效应变分布。由图6b可以看出，TC17合金双性能盘等温预锻后的局部等效应变分布范围为0.22～0.91，其中最大等效应变位于盘心的上下表面区域，由于变形不均匀使得整个盘的局部等效应变分布极不均匀。此外，在盘的毛边和辐板的过渡圆弧区域还存在3个较大的等效应变区域。图6c为TC17合金双性能盘等温终锻后的局部等效应变分布。可以看出，盘心区域的等效应变低于0.22，该区域为低应变区域；辐板区域的等效应变为0.22～0.69，该区域为中应变区域；盘缘区域的等效应变为0.69～1.2，该区域为大应变区域。由以上分析可以看出，优化设计后的预成形形状经多道次等温锻造后的等效应变分布满足目标应变分布的设计要求，采用该预成形形状进行等温锻造，可通过主动控制应变获得理想的有序渐变双重组织，为TC17合金双性能盘的研制提供理论依据。

表2 采用拉丁超立方试验设计方法抽样的设计变量及采用式（1）计算获得的响应应变误差

Tab.2 Selected values of design variables using LHS method and corresponding strain error in Eq.(1)

图4 预成形形状优化的流程

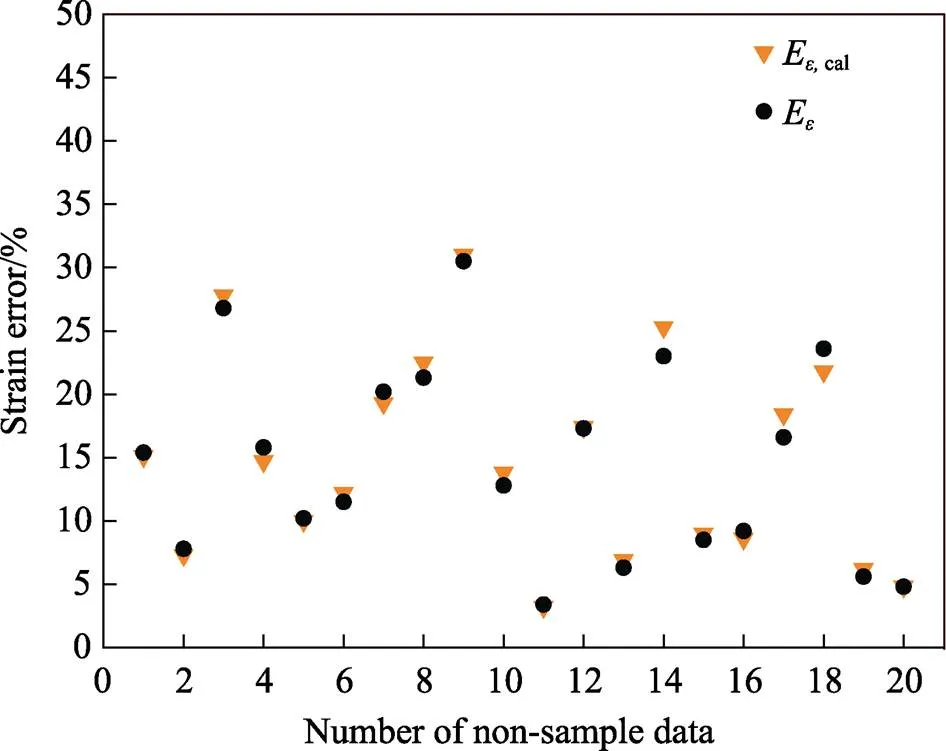
图5 Kriging模型预测的应变误差与基于有限元数值模拟计算获得的应变误差之间的比较

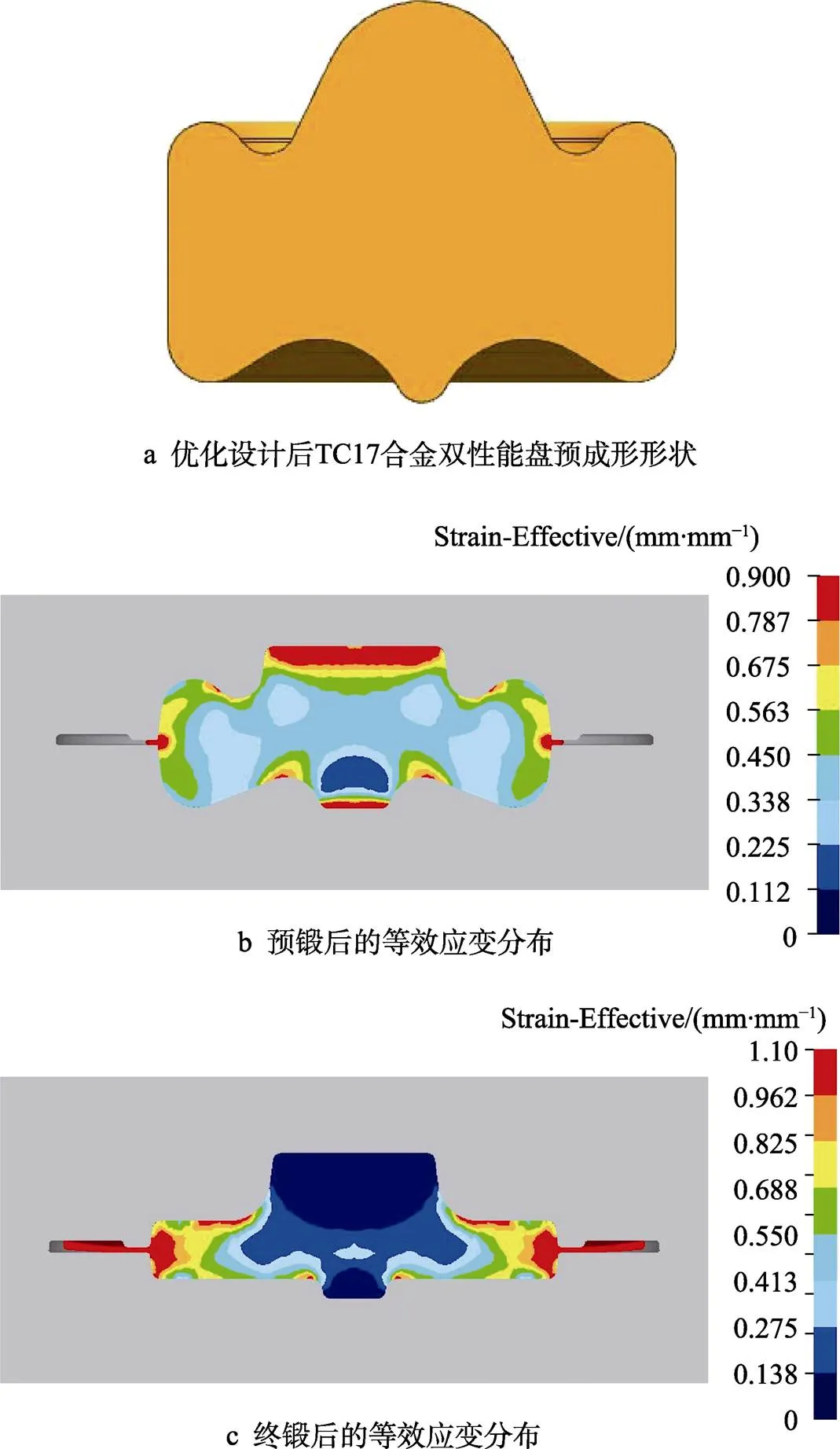
图6 优化后的坯料形状和变形后的等效应变分布

3 结论

采用拉丁超立方试验设计、Kriging近似替代模型、Deform有限元数值模拟和遗传算法相结合的方法，实现了TC17合金双性能盘目标应变分布下的预成形形状优化设计。设计过程中以局部应变分布与目标应变分布之间的方差最小为目标函数，采用Kriging近似替代模型预测的应变误差与基于有限元数值模拟计算获得的应变误差之间的最大相对误差和最小相对误差分别为10.8%和0.01%，这表明Kriging近似替代模型在预测应变误差时的精度较高，具有较好的可靠性。将优化后的设计变量进行验证性数值模拟，发现优化设计后的预成形形状经多道次等温锻造后的等效应变分布满足目标应变分布的设计要求，有望通过主动控制应变获得理想的有序渐变双重组织。

[1] SEMIATIN S L, SEETHARAMAN V, WEISS I. Flow Behavior and Globularization Kinetics during Hot Working of Ti-6Al-4V with a Colony Alpha Microstructure[J]. Materials Science and Engineering A, 1999, 263: 257—271.

[2] JIA Jian-bo, ZHANG Kai-feng, LU Zhen. Dynamic Globularization Kinetics of a Powder Metallurgy Ti-22Al-25Nb Alloy with Initial Lamellar Microstructure during Hot Compression[J]. Journal of Alloys and Compounds, 2014, 617: 429—436.

[3] LONG Shuai, XIA Yu-feng, WANG Peng, et al. Constitutive Modelling, Dynamic Globularization Behavior and Processing Map for Ti-6Cr-5Mo-5V-4Al Alloy during Hot Deformation[J]. Journal of Alloys and Compounds, 2019, 796: 65—76.

[4] GAO Yan, MA Guang-qi, ZHANG Xiao-yong, et al. Microstructure Evolution and Hot Deformation Behavior of Ti-6.5Al-2Zr-1Mo-1V Alloy with Starting Lamellar Structure[J]. Journal of Alloys and Compounds, 2019, 809: 151812.

[5] LUO Jiao, YE Peng, HAN Wen-chao, et al. Collaborative Behavior inLamellae andPhase Evolution and Its Effect on the Globularization of TC17 Alloy[J]. Materials and Design, 2018, 146: 152—162.

[6] ZHAO Xin-hai, ZHAO Guo-qun, WANG Guang-chun, et al. Preform Die Shape Design for Uniformity of Deformation in Forging Based on Preform Sensitivity Analysis[J]. Journal of Materials Processing Technology, 2002, 128(1/2/3): 25—32.

[7] ZHAO Guo-qun, WRIGHT E, GRANDHI R V. Sensitivity Analysis Based Preform Die Shape Design for Net-shape Forging[J]. International Journal of Machine Tools and Manufacture, 1997, 37(9): 1251—1271.

[8] GAO Zhen-yan, GRANDHI R V. Microstructure Optimization in Design of Forging Processes[J]. International Journal of Machine Tools and Manufacture, 2000, 40(5): 691—711.

[9] SUNDARARAGHAVAN V, ZABARAS N. A Multi- length Scale Sensitivity Analysis for the Control of Texture-Dependent Properties in Deformation Processing[J]. International Journal of Plasticity, 2008, 24(9): 1581—1605.

[10] SHAO Yong, LU Bin, OU Hen-gan, et al. Evolutionary Forging Preform Design Optimization Using Strain- Based Criterion[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(1/2/3/4): 69—80.

[11] SHAO Yong, LU Bin, OU Hen-gan, et al. A New Approach of Preform Design for Forging of 3D Blade Based on Evolutionary Structural Optimization[J]. Structural and Multidisciplinary Optimization, 2015, 51(1): 199—211.

[12] CHEN Hao, ZHAO Guo-qun, ZHANG Cun-sheng, et al. Numerical Simulation of Extrusion Process and Die Structure Optimization for a Complex Aluminum Multicavity Wallboard of High-Speed Train[J]. Materials and Manufacturing Processes, 2011, 26(12): 1530—1538.

[13] CHEN Hao, ZHAO Guo-qun, ZHANG Cun-sheng, et al. Effects of Multi-Step Welding Chamber on Extrusion Product Quality and Die Strength[J]. Applied Mechanics and Materials, 2011, 44/45/46/47: 311—315.

[14] GUAN Jing-yun, WANG Guang-cun, GUO Tong, et al. The Microstructure Optimization of H-Shape Forgings Based on Preforming Die Design[J]. Materials Science and Engineering A, 2009, 499(1/2): 304—308.

[15] PARK H S, AYU F R, KUMAR S. Preform Optimization for Bevel Gear of Warm Forging Process[J]. Procedia CIRP, 2018, 72: 340—345.

[16] NGO N V, HSU Q C, LI W H, et al. Optimizing Design of Two-Dimensional Forging Preform by Bi-Directional Evolutionary Structural Optimization Method[J]. Procedia Engineering, 2017, 207: 520—525.

[17] YOON J W, CHUNG K, POURBOGHRAT F, et al. Design Optimization of Extruded Preform for Hydroforming Processes Based on Ideal Forming Design Theory[J]. International Journal of Mechanical Sciences, 2006, 48(12): 1416—1428.

[18] LUO Jiao, LI Miao-quan, YU Wei-xin. Microstructure Evolution during High Temperature Deformation of Ti-6Al-4V Alloy[J]. Rare Metal Materials and Engineering, 2010, 39(8): 1323—1328.

[19] HAN Zhong-hua, GÖRTZ S. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling[J]. AIAA Journal, 2012, 50(9): 1885—1896.

[20] KRIGE D G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand[J]. Journal of the South African Institute of Mining and Metallurgy, 1994, 94(3): 95—111.

[21] JEONG S, MURAYAMA M, YAMAMOTO K. Efficient Optimization Design Method Using Kriging Model[J]. Journal of Aircraft, 2005, 42(2): 413—420.

[22] ZHANG Lei-gang, LU Zhen-zhou, WANG Pan. Efficient Structural Reliability Analysis Method Based on Advanced Kriging Model[J]. Applied Mathematical Modelling, 2015, 39(2): 781—793.

[23] JONG K D. Evolution Computation: Recent Developments and Open Issues[C]// Evolutionary Algorithms in Engineering Computer Science, Finland, 1999: 43.

[24] KAYMAZ I. Application of Kriging Method to Structural Reliability Problems[J]. Structural Safety, 2005, 27(2): 133—151.

Preform Shape Optimization Design for Acquiring Desired Strain Distribution during Forging of TC17 Alloy Dual-Microstructure Disks

ZHAI Jiang-bo

(AVIC Shaanxi Hong Yuan Aviation Forging Company Ltd., Sanyuan 713801, China)

The work aims to propose a method of preforming shape optimization design for TC17 alloy dual-microstructure disks with a desired strain distribution. In the present study, the latin hypercube sampling (LHS) method is applied to select the sample data for the shape design variables, and the local strain field for the sample design variables in dual-microstructure disks is simulated using the Deform finite element (FE) method. The objective function is established by minimizing the variance of local strain distribution and desired strain distribution in the whole forging. The approximate model is established based on Kriging equation to predict this corresponding strain error. Finally, the preform shape with two constrains (filling the die cavity and the volume constancy with less flash) is optimized and designed by the genetic algorithm. The results show that the maximum and minimum difference between the predicted strain errors by Kriging approximate model and FE simulated strain errors is 10.8% and 0.01%, respectively, indicating that the prediction accuracy of Kriging approximate model is very high and relatively reliable. After the preform is isothermally forged, the effective strain distribution is close to the desired strain distribution of TC17 alloy dual-microstructure disks.

TC17 alloy; Kriging model; FE numerical simulation; genetic algorithm; optimization design

10.3969/j.issn.1674-6457.2021.03.014

TG319

A

1674-6457(2021)03-0118-07

2021-02-13

翟江波（1981—），男，高级工程师，主要研究方向为航空材料锻造工艺。