面向海洋观监测传感网的计算卸载方法研究

苏新，薛淏阳，周一青，朱金秀

（1.河海大学物联网工程学院，江苏 常州 231022；2.中国科学院计算技术研究所，北京 100190）

1 引言

海洋观监测传感网作为海洋信息网络的重要组成部分可提供多种观监测应用，是汇聚海洋空间、环境、资源等各类数据的重要平台。全天候、全自动的海洋观测和目标态势感知、海洋信息传输，以及海上综合业务服务的开展，提出了实时定位、紧急救援以及面向某些领域的低时延信息服务需求，这对海洋观监测传感网支持低时延高可靠的观监测应用提出了极高的要求。进入5G/6G时代[1-2]，海洋观监测传感网络终端设备（OUE,oceanic user equipment）对于低时延高可靠的应用需求随之增加，需要全新的数据处理方式以满足相关应用需求。

2014 年，欧洲电信标准协会提出了移动边缘计算概念，并于 2016 年扩展为多接入边缘计算（MAEC,multi-access edge computing）[3]。其主要思想是将云计算的部分业务下沉至网络边缘，在用户边缘分布式地部署服务与存储，以快速地为用户提供服务，极大减少回传网络带宽[4]。在网络边缘就近处理数据的边缘计算方式可实现终端用户对低时延、高可靠的要求[5]。因此，将边缘计算关键技术引入海洋观监测传感网以满足低时延、高可靠的海事应用需求具有极高的研究意义和应用价值。

计算卸载技术作为边缘计算的关键技术，对降低用户执行时延，提升用户服务质量起着重要作用[6]。现阶段边缘计算卸载技术研究主要围绕陆地组网与车联网，普遍根据其组网特征进行研究[7-8]。由于海洋环境复杂多变，不能简单地将现有陆地组网中的MAEC 卸载技术应用于海洋观监测传感网。因此，将MAEC 卸载机制引入海洋观监测传感网的研究会面临以下挑战。

1) 海洋场景节点密度变化明显，边缘计算资源分布不均，调度困难，网络节点计算与通信资源存在差异。例如，各个节点对时延和能耗的敏感度不同，网络局部产生的大量数据会导致网络超负荷处理，系统面临瘫痪危险。

2) 海洋观监测传感网终端设备移动速度不同，网络拓扑变化快，节点间通信范围存在差异且有效通信时间不同，容易导致传输链路中断。

通过参考MAEC 卸载技术在陆地组网及车联网中的研究[7]，结合海洋观监测传感网中存在的挑战，本文以满足低时延、高可靠的海事应用需求为目标，研究了海洋观监测传感网中的MAEC 卸载技术，主要贡献如下。

1) 针对节点密度差异化下的卸载问题，提出了以下2 种卸载模型：在网络节点高密度的近岸区域，计算资源丰富，多用户计算卸载可用多个独立的单用户多边缘节点模型等效；在网络节点低密度的远岸区域，计算资源匮乏，多用户计算卸载需考虑协同，提出远岸双跳多用户模型。同时，阐述了一种基于海洋网络连通概率的边缘节点选取方法，使终端用户可选取该区域内有利于其卸载传输的最佳节点。

2) 提出了节点间有效通信时间约束，并分别引入近岸和远岸2 种卸载模型，保证了用户数据卸载时网络的连通效率。

3）在选取边缘计算节点基础上，提出了2 种计算卸载算法，在2 种卸载模型下实现了用户卸载时的最佳决策和资源调度，解决了节点间资源差异导致的网络成本增加的问题。

2 相关工作

计算卸载相关研究工作按照系统模型可分为单用户设备（SUE,single user equipment）计算卸载和多用户设备（MUE,multi-user equipment）计算卸载，本文将分别对这2 种工作进行分析与讨论。

2.1 单用户设备计算卸载

目前，针对SUE 计算卸载的研究主要分为单用户与单个MAEC 服务器（简称为SUE-SMAEC）、单用户与多个MAEC 服务器（简称为SUE-MMAEC）。

文献[9]针对SUE-SMAEC，运用一维查询算法根据UE和MAEC服务器的计算资源及其之间的信道特征找到最优的卸载策略，实现最小化执行时延的目标。然而，文献[9]未考虑能耗约束会导致UE 能耗过高。为同时满足UE 对时延与能耗的要求，文献[10]提出了在满足应用执行时延的同时最小化用户能耗的卸载策略。优化方法引入了在线学习和离线预先计算2 种卸载方案。与全部卸载相比[9-10]，部分卸载更灵活，允许用户将任务在本地和MAEC 服务器分别执行。文献[11]假设UE 应用由多个子任务组成，各任务之间相互依赖，并提出了基于二元粒子群的卸载算法，使部分卸载相对于全部卸载具有显著的节能效果。

针对车联网下的计算卸载，文献[4]研究了在SUE-MMAEC 中任务分配和卸载决策的问题。文献[4]虽然考虑了节点移动性，但并未对其可能产生卸载中断问题进行分析解决。针对车联网中车辆快速移动导致的卸载中断问题，文献[12]提出了一种避免传输中断的自适应卸载策略，考虑车速、传输速率等因素对卸载的影响，并根据这些因素动态调整卸载策略，避免卸载过程中的传输中断。

目前，SUE 计算卸载的研究主要围绕陆地组网和车联网 2 种场景，且多数卸载方案仅考虑SUE-SMAEC 的全部卸载和部分卸载，较少考虑多MAEC 服务器协同处理的卸载方式。

2.2 多用户设备计算卸载

通常，由于MAEC 系统中通信和计算资源有限，难以满足过多终端用户的计算卸载需求，且分布式计算场景之间难以达到MAEC 资源的有效利用[13]。因此，学者们开始关注MUE 场景下的卸载研究，以实现资源的合理分配。

文献[14]将MUE 系统中资源分配表述为一个非线性问题，提出一种基于贪婪策略的资源分配方案，有效地降低了终端能耗。不同于通过贪婪策略进行资源分配，文献[15]提出了阈值结构的资源分配策略。在时分多址MUE 系统中，通过本地计算能力和信道增益的卸载优先级函数确定用户优先级，基站根据用户优先级与阈值间的关系，决定用户卸载的数据量。文献[16]综合考虑卸载决策、信道状态、计算资源等影响因素，将超密集网络下的计算卸载模型表述为一个混合整数非线性规划问题，设计了一种结合遗传和粒子群的优化算法，以此实现最优资源分配。

以上方案均从降低系统时延或能耗角度出发，并未从用户对能耗和时延的敏感程度差异角度对系统时延和能耗进行综合优化。文献[17]在MUE-SMAEC 系统中，首先针对用户对能耗和时延差异度，为其设置相应能耗时延优化比；再将卸载决策和资源分配的优化表述为非凸优化问题，通过鲸鱼遗传算法解决不同用户需求；最终实现资源分配。但文献[17]中算法的迭代速度相对较慢，增加了系统成本。针对计算资源分布不均的问题，文献[18]在MUE-MMAEC 系统中通过主辅MAEC 服务器协同处理的方式，运用模拟退火算法进行卸载决策和资源分配的联合优化，解决了资源分布不均导致的资源调度困难问题。

基于以上论述，现有MUE 计算卸载研究主要以减少终端能耗和任务执行时延为优化目标，对综合考虑优化任务时延和终端能耗的研究较少，且均未考虑MUE 系统中计算卸载的可靠性。算法迭代速度都相对较慢，难以保证较小的计算卸载成本，无法满足海洋观监测传感网的各类海事应用需求。

3 海洋网络系统模型

图1 展示了本文提出的海洋网络系统模型，通常，距离海岸37.04 km（即20 海里）为近岸海域，海域界限向外一侧的为远岸海域[19]。海洋网络中，不同海域节点密度差异明显，近岸海域由于海事活动较频繁，通常其网络节点密度高于远岸海域。

在海洋网络中，网络节点一般包含大型船舶、浮标、小型船只、水下机器人以及基站等。小型船只和浮标由于自身资源有限，一般难以独自完成数据处理，需要传输至其他节点进行处理。大型船舶与基站等相比浮标等节点计算能力较强，可充当边缘计算节点来处理终端用户卸载的数据。通常，基站计算能力强于大型船舶，在近岸海域，可通过多个海岸基站与大型船舶协同实现用户的计算卸载；在远岸海域，由于海域范围广，大规模建设成本投入大等因素，本文考虑在远岸海事活动频繁的海域建设1～2 个大型海上基站保证海事应用需求，尽可能地利用现有设施满足海事应用需求。

结合相关工作讨论可知，单用户模型一般用于解决资源丰富情况下如何实现高效卸载决策与资源调度，以满足OUE 应用需求的问题。近岸海域计算资源丰富，某一区域内可用计算资源较多，需要考虑OUE 如何充分利用资源，以满足自身需求。因此，结合单用户模型特性，近岸海域本文提出单用户多边缘节点模型。如图1 所示，该模型主要由集中控制单元、边缘计算节点（包含海岸基站、大型船舶等）以及OUE（包含浮标、小型船只等）组成。OUE 可以通过多个边缘计算节点协同处理计算任务，调度近岸丰富的计算资源以满足自身需求。

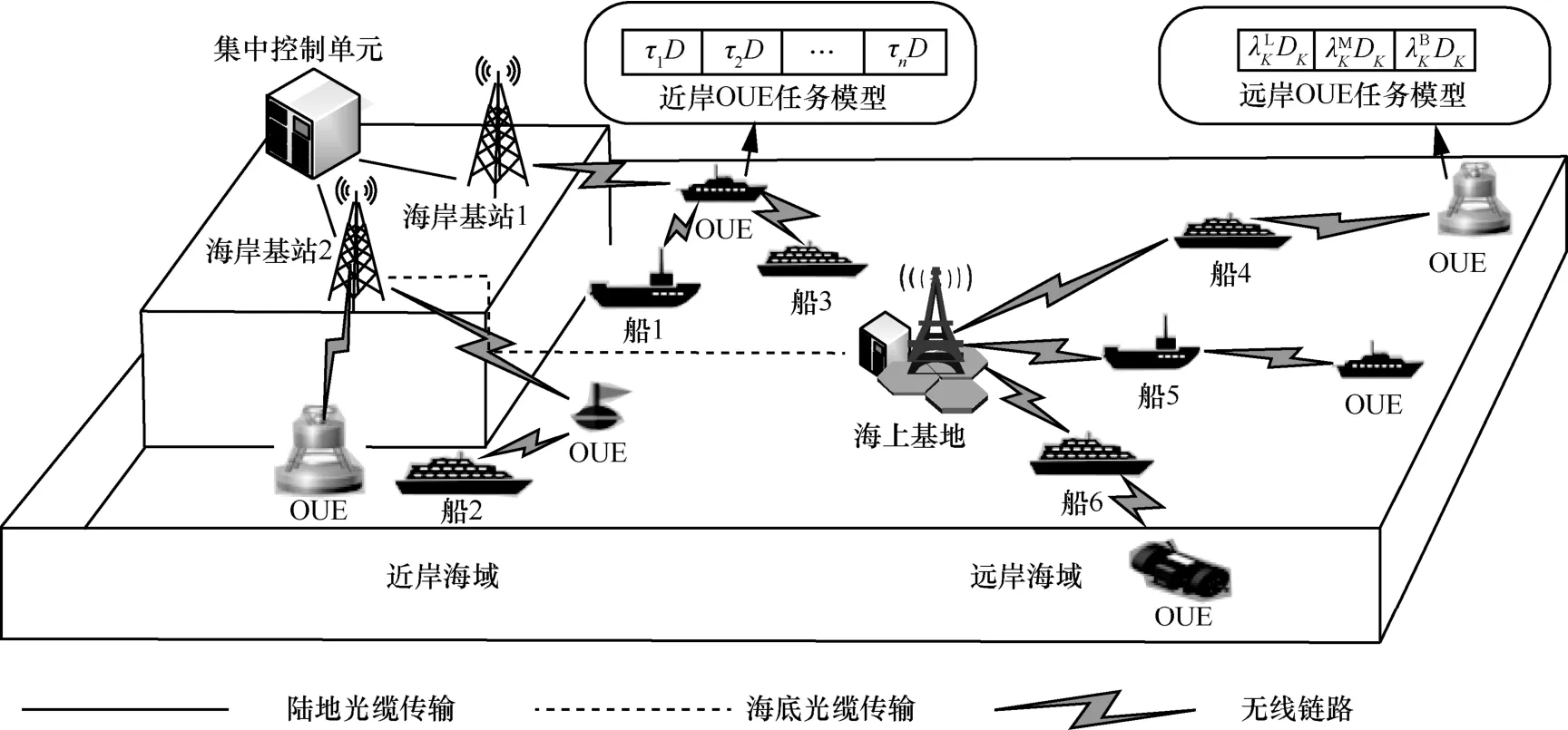
图1 海洋网络系统模型

多用户模型一般用于解决资源匮乏时如何实现资源的合理分配利用，以满足多个用户的卸载需求。远岸海域计算资源匮乏，在同一区域内多个用户同时卸载可用计算资源相对较少，需要考虑有限资源的合理分配。此外，远岸海域范围广，节点离散化分布，OUE 可能远离海上基站（OBS,offshore base station），这使远离OBS 的OUE 需要多跳传输完成卸载。通常，多于两跳的卸载由于时延与能耗开销巨大，不符合低时延高可靠的海事应用需求。因此，如图1 所示，本文面向远岸海域提出了双跳多用户模型，主要由OBS、中继节点（大型船舶等组成）、K个OUE 等组成。OUE 可将计算任务卸载至OBS 和各自的中继节点，从而在满足OUE 卸载的同时，实现资源的合理分配。

由于海洋网络节点间资源差异明显，OUE 计算卸载能耗与时延受到边缘节点资源影响。如OUE 任务卸载至通信条件较好、计算能力较强的节点，卸载时延较低。需要OUE 选取合适的边缘计算节点使OUE在计算卸载时拥有良好的卸载条件十分必要。本文结合前期研究基础[19]提出基于海洋网络连通概率的边缘计算节点选取方法，该方案适用于近岸与远岸2 种场景，包含海洋网络连通概率预测和边缘计算节点确定2 个步骤，具体如下。

图2 为相邻船舶通信示意。基于前期对海洋网络中节点间连通概率预测研究[19]，船与船之间连通概率为

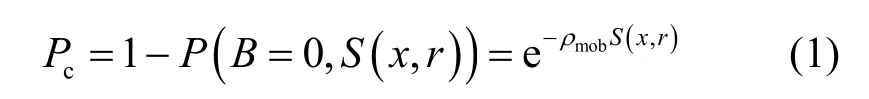
其中，ρmob表示船舶密度（艘/海里，与船舶速度有关），S(x,r)表示船A 与船B 通信范围交集（如图2中灰色区域所示），B表示S(x,r)内存在船舶的数量，P(B=0,S(x,r))为两船通信范围内没有船舶的概率，x和r分别表示两船间距离和船舶通信半径，且x、r与S(x,r)存在如下关系

图2 相邻船舶通信示意

图3 为船舶与基站通信示意。船舶与基站间连通概率受两基站间距离L、基站覆盖半径R、船舶通信半径r及船舶到基站的距离x影响。结合图3给出了基站与船舶连通概率Ps[19]。

1) 当0＜L≤2R，x∈[ 0,L]时，Ps=1。

2) 当2R＜L≤2R+r，x∈(0,R) ∪(L−R,L)时，Ps=1。

3) 当2R＜L≤2R+r，x∈(R,L−R)时，

4) 当 2R+r＜L≤2R+2r，x∈(0,R)∪(L−R,L)时，Ps=1。

5) 当2R+r＜L≤2R+2r，x∈(R,L−R)时，

6) 当L＞2R+2r时，

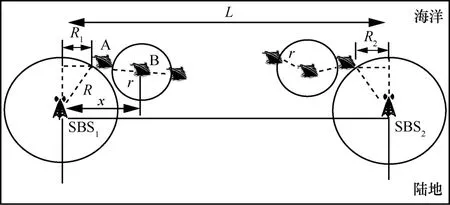
图3 船舶与基站通信示意

根据以上船−船、船−基站之间连通概率，可求得OUE 与该区域内各节点之间的连通概率。将连通概率大于阈值Py的节点作为连通节点，可保障良好的计算卸载通信条件。

基于海洋网络连通概率预测模型，选择网络中计算能力和通信资源较好的海洋连通节点作为OUE 的边缘计算节点。可通过式(6)计算具体OUE与第k个连通节点之间的边缘系数Sk∈(0,1)，根据每个连通节点的边缘系数与阈值Sy之间的关系确定边缘计算节点。

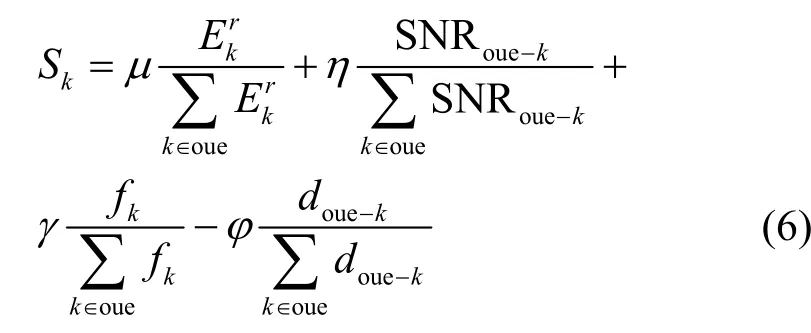
其中，μ+η+γ+ϕ=1。

当Sk≥Sy时，选取第k个连通节点作为OUE边缘计算节点。式(6)中第一部分表示第k个连通节点的剩余能量占OUE 所有连通节点能量和的比重，值越大表示该节点相对OUE 的其他节点的能量优势越大；第二部分为OUE 与第k个连通节点间的信噪比SNRoue−k在OUE 所有连通节点中的占比，值越大表示该节点与OUE 间的传输条件越好；第三部分表示第k个连通节点的计算能力fk在OUE 所有连通节点中的占比，值越大表示该节点相比OUE 的其他节点计算能力越强；第四部分为OUE 与第k个连通节点之间的距离doue−k占OUE 所有连通节点距离和的比重，值越小表示该节点与OUE 间的数据传输能耗与时延越小。

4 基于多点协同的近岸计算卸载方法

4.1 近岸海域卸载流程描述

OUE 多应用并行执行（如自动定位系统、资源探测应用、娱乐应用等）会集中产生大量需要实时处理的数据。假设数据D可被分割成N个不同数据量的计算任务，表示为N={Nloc,Noff}={τ1D,τ2D,…,τnD}，其中Nloc和Noff分别表示在本地执行或计算卸载的任务数量；τnD表示任务n需要处理的数据量，τn表示任务n数据量分配比例且

当OUE 发送卸载请求至集中控制单元，控制单元通过获取OUE 附近节点信息，制定最佳卸载方案。控制单元将卸载方案XN={x1,x2,…,xn}（其中，xn表示任务n卸载至编号为xn的边缘计算节点，xn=0表示本地执行）发送至OUE。OUE 按照卸载策略将任务分别在本地处理或卸载至不同的边缘计算节点。各边缘计算节点将执行结果回传至OUE。

当任务n在本地执行时，需要处理的数据量为τnDbit 。设本地计算能力为foue（即每秒CPU 周期数），cn为计算1bit 数据所需的CPU 周期数，与任务复杂度有关。设Ploc为OUE 的计算功率，因此任务n在本地处理所需时间和能耗可表示为

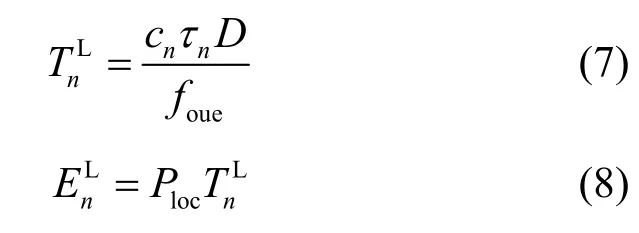
当任务n卸载至边缘计算节点执行时，由于海洋观监测传感网中各节点具有移动性且轨迹不同；OUE 在卸载时，首先需要考虑OUE 与边缘计算节点间的有效通信时间，确保OUE 在计算卸载时不会出现通信中断的问题。如图4 所示，可设船A 速度为v1，船B 速度为为速度v2与i轴的夹角），当船B 进入船A 有效通信范围时，直线A—B与i轴夹角为β。另设船B进入船A有效通信范围后沿线路行驶，则船A与船B 有效通信时间为

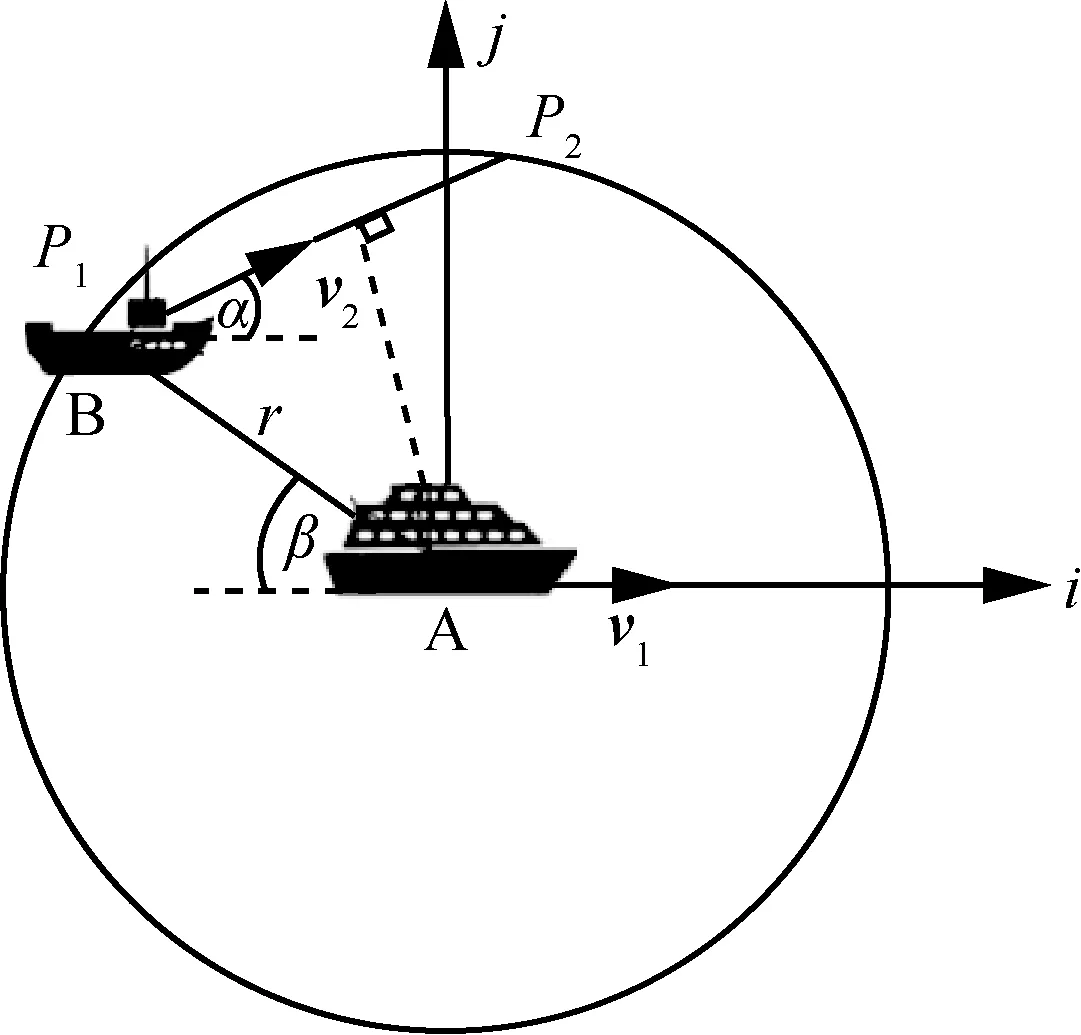
图4 相邻两船通信示意

在保证卸载不会中断之后，任务n卸载时，设fmaec(xn)为边缘节点xn的计算能力，Ptran表示OUE传输功率，任务n卸载所需时间为

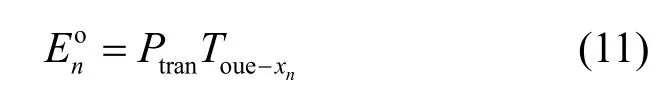
近岸海域OUE 的总执行时间Toue受卸载决策XN和任务分配系数τ影响。由于各任务之间可并行执行，卸载部分所用时间取决于边缘节点中执行时间的最大值。为了最小化OUE 时延，近岸区域卸载时延优化目标如式(12)所示，其中第一部分表示本地计算部分的总执行时延，第二部分表示卸载部分的总执行时延。约束a 表示任务卸载执行时延不大于任务n本地计算时延及OUE 与边缘节点xn的通信时间；约束b 表示任务n卸载能耗不超过该任务本地计算能耗；约束c 表示各任务的数据量之和应等于OUE 需要处理的总数据量；约束d 表示每个任务只能卸载至一个边缘节点。

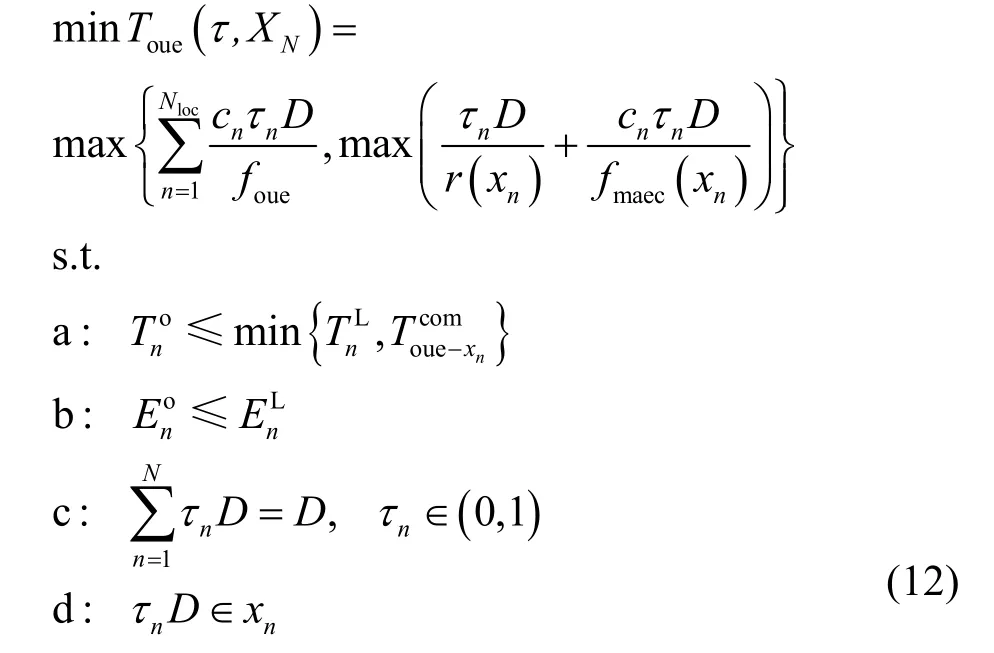
4.2 近岸海域多节点协同卸载优化方法

为了解决近岸多节点协同机制下卸载优化问题，本文提出一种基于海洋多节点协同卸载的遗传算法（MCO-GA,maritime multi-node cooperative offloading based genetic algorithm）。该算法通过对遗传算法（GA,genetic algorithm）中编码方式及适应度函数的优化与改进，使OUE 在寻找到最优卸载策略的同时可有效降低时延。

4.2.1遗传算法

GA 通过模拟自然进化过程来搜索最优解，染色体编码时每条染色体经过编码可以看作优化问题的一种解。染色体的编码影响后续的交叉、变异操作，很大程度上决定了GA 的进化效率。适应度函数是根据目标函数确定的用于区分种群中个体好坏的标准。在染色体种群中，个体的适应度值越大，表明该个体越适应环境。

选择操作以一定概率从种群中选择若干个体。选择过程基于适应度优胜劣汰机制。通过计算，每个染色体被赋予一个适应度值，这些值与个体被选择的概率相关。本文卸载优化策略采用轮盘赌选择方式[20]，假设种群数量为S，A1,A2,…,Ai表示当前种群中每个可能解，个体i的适应度为fitness(Ai)，因此该个体被选中的概率为

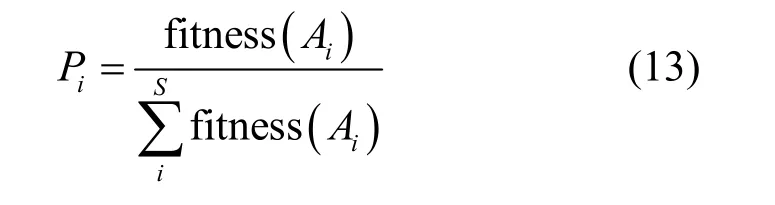
在进行交叉操作时，本文采用单点交叉的方式且交叉概率为PJ，具体操作是在个体编码串中随机设定一个交叉点，实行交叉时，该点前或后2 个个体的部分结构互换，从而生成2 个新个体。在变异操作中本文采用基本位变异方式，变异概率为Pm，随机指定一位或多位点做变异运算得到新个体，可防止算法过早收敛。

4.2.2基于海洋多节点协同卸载的遗传算法

MCO-GA 通过对超出可行域的染色体增加惩罚值，使其适应度值减小，在选择操作时不易被选中；把近岸约束优化问题转化为无约束问题，最终实现在可行域内的最优计算卸载策略求解。

在对优化变量进行编码时，由于采用固定边缘节点与移动边缘节点协同卸载的策略；因此需要对OUE 每个边缘节点进行编号后，将OUE 各任务进行卸载的边缘计算节点编号及各边缘节点的任务分配比例采用二进制编码的方式表示在每条染色体上。其中，任务卸载的边缘计算节点编号及任务分配比例分别用卸载决策XN和数据量分配比例τ表示。优化变量编码过程如图5 所示，x1−xn，τ1−τn分别表示任务卸载决策和任务分配比例。图5 中列举了卸载决策变量x1的二进制表示方法，其他变量同理。

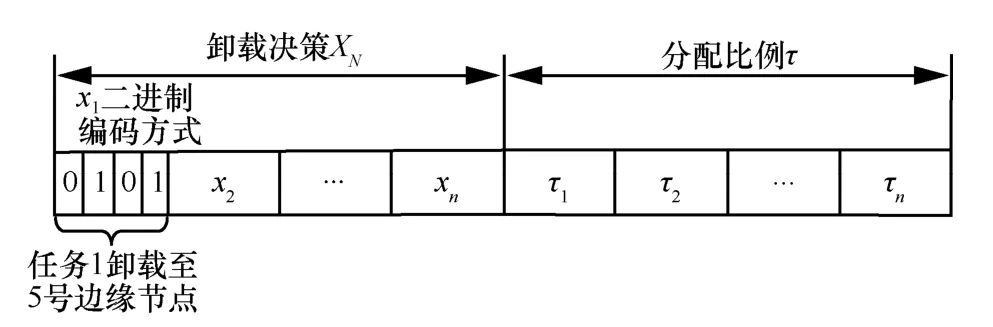
图5 优化变量编码过程

由于GA 面向非约束优化过程，而本文考虑了约束优化问题。因此，需要通过引入惩罚函数将约束优化问题转化为无约束优化问题进行分析，且适应度函数可表示为

其中，penalty(Ai)为惩罚函数（通过对非可行解的个体增加惩罚值使其被选择的概率降低），表示为

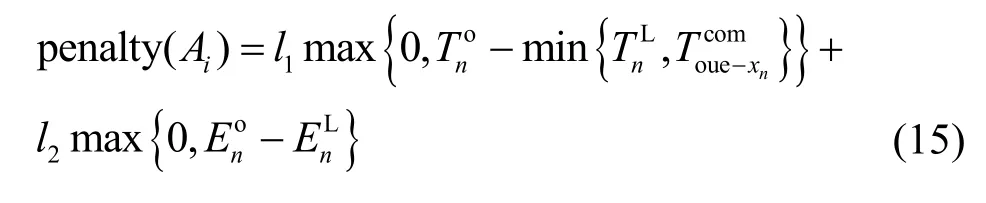
其中，l1和l2为正惩罚因子。

结合海洋船舶运动轨迹的特殊性[19]，需要考虑船舶间速度方向不同以及通信半径差异产生的通信时间变化问题。因此，惩罚函数考虑了有效通信时间（式(9)）等因素，从而避免了OUE 计算卸载时通信中断问题。惩罚函数通过对卸载能耗进行约束，保证了OUE 计算卸载时较低的能耗。

4.2.3基于MCO-GA 的优化策略

本文中每条染色体表示一种卸载策略Ai，其中每一种卸载策略Ai包括卸载决策XN与数据量分配比例τ。此外，卸载策略Ai交叉变异操作前后的适应度可分别用fitness(Ai)与fitnessn(Ai)表示，适应度值包括该卸载策略下 OUE 对应的执行时延Toue(Ai)及相应的惩罚值penalty(Ai)。图6 描述了MCO-GA 的流程，具体如下。

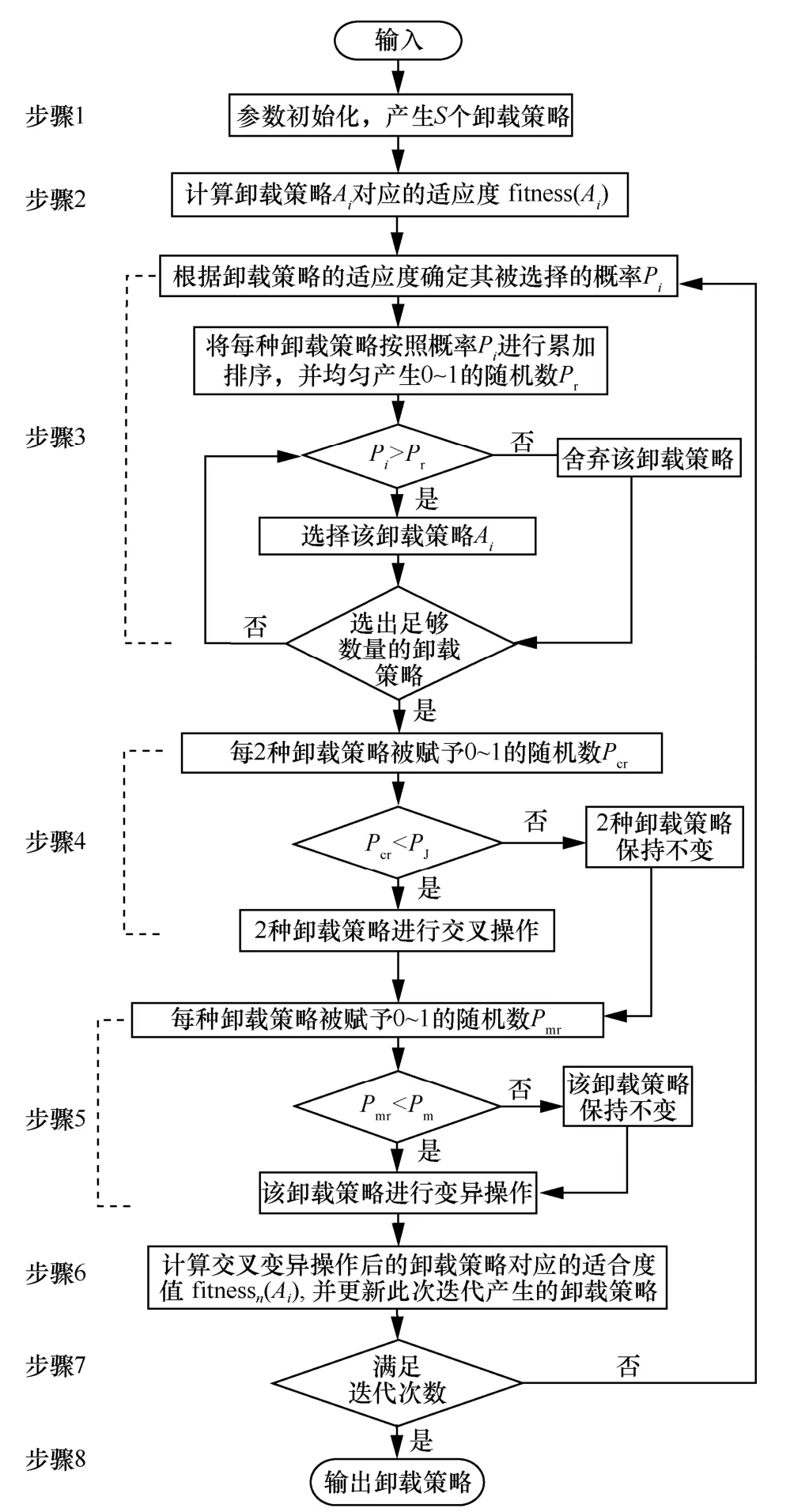
图6 基于MCO-GA 算法的优化策略流程

输入边缘计算节点计算能力fmaec(xn)、OUE计算能力foue、任务数量N、OUE 本地计算功率Ploc、OUE 传输功率Ptran和任务n计算复杂度cn。

输出最优卸载决策XN、最优数据量分配比例τ、最优卸载策略对应时延。

步骤1初始化。确定迭代次数itera_num 与染色体数量S（每次迭代不同的卸载策略数目），同时设置卸载策略交叉操作与变异操作的概率分别为PJ和Pm，在可行域内随机产生S个卸载策略。

步骤2计算适应度。根据式(14)的适应度函数计算每种卸载策略对应的适应度。

步骤3选择操作。根据式(13)计算每种卸载策略Ai被选中的概率Pi，将本次迭代中所有可能的卸载策略按照其概率大小进行累加排序。同时均匀产生S个0～1 的随机数Pr。若Pi＞Pr，则选择该卸载策略进行后续操作，直至选出足够数量的卸载策略。

步骤4交叉操作。每2 种卸载策略一组，被赋予0～1 的随机数Pcr（该值作为是否进行交叉操作的判断依据）。若Pcr＜PJ，则该组2 种卸载策略进行交叉操作，产生2 种新的卸载策略；否则2 种策略保持不变。

步骤5变异操作。每种卸载策略被赋予0～1的随机数Pmr（作为是否进行变异操作的判断依据）。若Pmr＜Pm，则随机选取该卸载策略上3 个点位进行变异操作。

步骤6更新种群。计算交叉变异操作后卸载策略Ai对应的适应度 fitnessn(Ai)，若fitnessn(Ai) ＞fitness(Ai)，则替换交叉变异前的卸载策略Ai。

步骤7终止条件判断。终止条件根据迭代次数itera_num 判断。若满足迭代次数，则选择出适应度值最小的卸载策略并退出循环；否则继续执行步骤3～步骤6，直至满足条件。

步骤8输出最优卸载策略Ai及对应时延Toue(Ai)。

5 基于容错重传机制的远岸计算卸载方法

5.1 远岸海域卸载流程描述

远岸海域计算资源相对匮乏且海域环境复杂，节点间通信链路易受到恶劣环境因素的影响而导致卸载失败。提出容错重传机制计算卸载方法考虑节点间可能出现的通信故障十分必要，可保证远岸海事应用的可靠性。

设远岸系统模型中继节点M={m1,m2,…,mk}（mk表示第k个OUE 的中继节点），OBS 计算能力强于中继节点，且OBS 与每个中继节点均可作为边缘计算节点。另设OUE 计算任务可分割，每个OUE 只能选择一个中继节点连接OBS。一般情况下，K个OUE 可同时向控制单元发送卸载请求。控制单元收到请求后为OUE 制定相应卸载策略。

OUEk全部任务在本地执行时延与能耗可表示

当ak=0且OUEk子任务在mk执行时，需要处理的数据量为设中继节点mk计算能力为，子任务卸载至mk执行时延可表示为

综上所述，容错机制下的计算卸载模型中，OUEk总执行能耗与时延可分别表示为

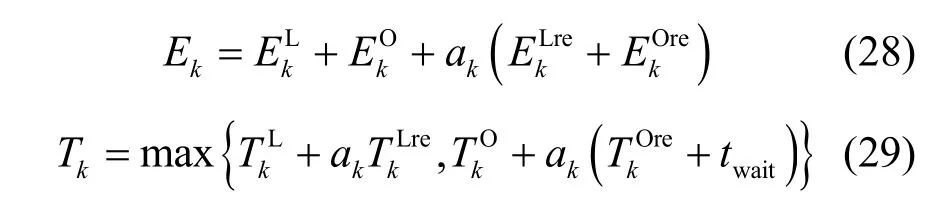
其中，twait为OUEk的等待时延，表示当OUEk在任务计划完成时间内未收到卸载任务的执行结果，则启动容错机制，先将原计划完成时间延长，若还未收到OBS 执行结果，则认为任务卸载失败，随后ak=0时分配给OBS 的任务做重传处理。由于不同OUE 对于能耗和时延的敏感程度存在差异。在计算卸载时要综合考虑OUE 对时延和能耗的要求，和IE,k分别表示OUEk在综合优化时所要求的时延和能耗比重，可根据OUE 需求进行调整。OUEk在执行任务时总开销（时延和能耗）为

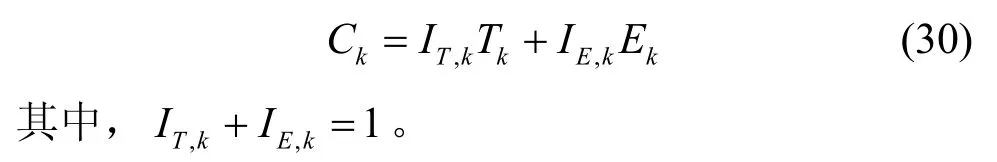
远岸计算资源匮乏区域可容错机制下，K个OUE 计算卸载受制于每个OUE 正常执行与故障执行下的任务分配比，以及正常执行情况下OBS 的计算资源分配比。针对不同OUE 的实际使用需求，远岸容错机制下卸载开销优化问题可由式(31)表示，其中λ={λL,λM,λB}且λL、λM、λB分别为K个OUE 在本地、中继节点、OBS 的任务分配比例集合。λre={λLre,λOre}，λLre、λOre分别表示重传情况下K个OUE 在本地和中继节点的任务分配比例。约束a 表示OUEk任务执行总时延不超过节点间有效通信时间及任务全部本地执行的最小值；约束b表示OUEk任务执行能耗不大于任务全部本地执行的能耗；约束c 表示正常执行和重传执行的任务分配比例取值范围；约束d 表示正常执行情况下，任务分配比例的和约束；约束e 表示重传情况下，任务分配比例的和约束；约束f 表示OBS 分配给K个OUE 计算资源不大于OBS 计算资源。

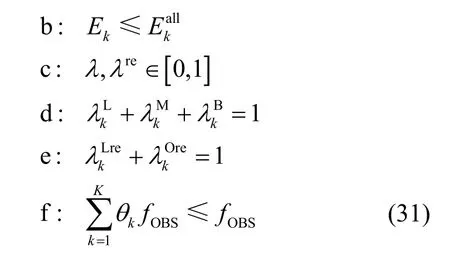
5.2 远岸海域可容错卸载优化方法

为解决远岸计算卸载优化问题，本文提出基于分组交叉学习的粒子群优化（GCL-PSO,group cross learning based particle swarm optimization）算法。由于此时优化变量和问题约束条件增多，传统群智能算法在求解问题时容易陷入局部最优。GCL-PSO 算法在传统PSO 算法基础上引入分组竞争学习，通过每个粒子分组交叉竞争学习，使其能够全面地在可行域内搜索最优解。GCL-PSO 算法较一般算法收敛速度快，处理复杂问题时能够实现快速优化。

5.2.1传统PSO 算法

PSO 算法设置粒子总数为particle_num，包含位置与速度因素[21]。第i个粒子的位置可看作优化问题的一种潜在解Qi，第i个粒子的速度hi表示粒子i位置更新的方向与距离。寻优过程中粒子i搜索到自身最优的位置表示为pbesti，粒子群中搜索到群体最优的位置表示为gbest。粒子i位置与速度更新计算过程表示为

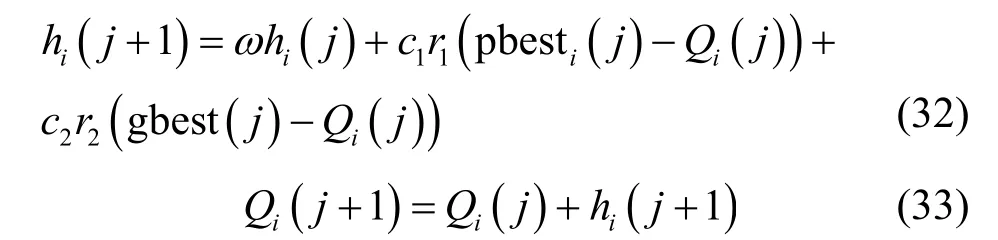
其中，j表示迭代次数，ω为惯性因子（值较大时全局寻优较强，值较小时局部寻优能力较强）；c1,c2为学习因子；r1和r2为0～1 的随机数。

5.2.2基于分组交叉学习的粒子群优化算法

本文为远岸卸载优化问题提出GCL-PSO 算法。结合传统PSO 算法中调节参数少、收敛速度快等优点。所提算法先对每个粒子进行分组，使其在小组内先进行局部学习，再通过粒子更新式进行全局学习。下面将介绍GCL-PSO 算法的具体实现过程。

GCL-PSO 算法初始化粒子参数后，将每个粒子进行随机分组。分组后根据适应度大小在组内排序。组内每个粒子依据排序顺序在组内相互学习，学习方式采用GA 的交叉操作。组内适应度较差的粒子通过向适应度较好的粒子学习获取新粒子，并将新粒子的适应度与交叉前的粒子适应度比较。若适应度优于交叉前的粒子，则将交叉前的粒子替换为交叉后的粒子，再将新粒子与当前个体极值与全局极值比较。若适应度优于当前个体极值或全局极值则将其替换，否则舍弃新粒子。

分组学习后将每个粒子从分组中拆分出来（下次迭代重新分组），根据分组学习后输出的pbesti与gbest，更新式(32)和式(33)进行全局学习，通过不断调整每个粒子位置与速度最终找到优化问题的最优解。

5.2.3基于GCL-PSO 算法的优化策略

GCL-PSO 算法相关参数与远岸卸载优化问题相关参数间的映射关系如表1 所示。

表1 GCL-PSO 算法参数与卸载策略参数映射

输入OUE 数量K、OUE 计算能力fk、中继节点计算能力、基站计算能力fOBS、OUE 本地计算功率、OUE 传输功率、OUE 传输带宽Wk、中继节点传输带宽和OUE 任务复杂度系数ck。

输出最优卸载策略和最优策略对应系统成本。

步骤1初始化。确定迭代次数GCL_itera 与粒子数量particle_num（每次迭代产生的卸载策略数量）在可行域内设置每个粒子初始位置QiN(j)与速度hi(j)。

步骤2系统成本计算。根据式(31)所示的优化问题计算正常情况下每种卸载策略所对应的系统总成本Ci(j)。将前j次迭代中粒子i系统成本最小时所对应的卸载策略设置为粒子i当前的个体极值pbesti(j)，同时设置当前粒子群中系统成本最小的粒子所对应的卸载策略为全局最优卸载策略gbest(j)。

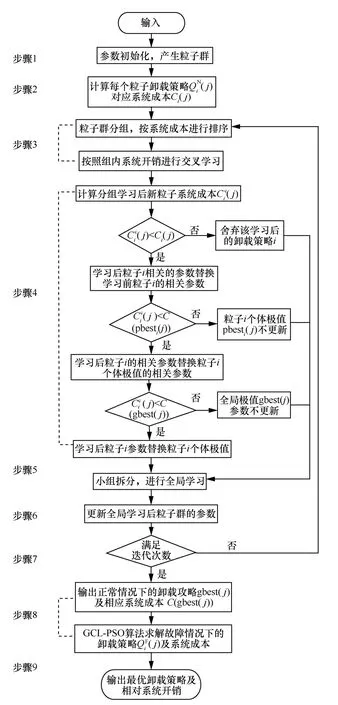
图7 GCL-PSO 优化方法流程

步骤3卸载策略分组竞争学习。每3 种卸载策略为一组进行随机分组。在组内按照每种策略所求得的系统成本Ci(j)对卸载策略进行排序，排序后系统成本值最大的策略采用交叉方式向组内次优策略学习，次优策略向成本值最小的策略学习。

步骤5粒子全局学习。根据式(32)和式(33)更新粒子i当前速度hi(j)与卸载策略每个粒子根据当前个体极值pbesti(j)与全局极值gbest(j)不断调整自身卸载策略。

步骤6更新全局学习后参数。求解全局学习后新粒子对应的系统总成本，根据系统成本更新每个粒子的个体极值pbesti(j)和全局极值gbest(j)。

步骤7终止条件判断。终止条件根据迭代次数进行判断。若满足迭代次数则退出循环，输出正常执行时的最优的卸载策略gbest(j)以及对应系统成本C(gbest(j))。若不满足则继续执行步骤3～步骤6，直至满足终止条件。

步骤8故障情况下最优策略求解。根据步骤7输出正常情况下最优卸载策略gbest(j)，运用GCL-PSO 算法求解故障情况下的卸载策略

步骤9输出最优卸载策略及对应的系统成本。输出每个OUE 的卸载策略（包含正常执行与故障执行2 种情况下的策略）以及对应的系统总成本。

6 实验仿真结果与分析讨论

6.1 近岸仿真结果分析

模拟OUE 在近岸场景下同时将多个任务卸载至固定边缘计算节点（基站）和移动边缘计算节点（船舶）的网络场景。实验仿真参数设置参考文献[4,17,19]，如表2 所示。为保证数值选取的均匀随机性，通信半径的设置基于文献[19]并进行了相应的调整；船舶速度的设置也主要参考文献[19]中的研究结果（该研究结论说明海洋网络中船舶速度与单位区域内船舶密度呈负相关，且近岸区域网络节点密度一般高于远岸区域）。因此，在表2 所示仿真实验场景下，设置近岸船舶速度大于远岸船舶速度。此外，通过多次实验，MCO-GA 在迭代100 次以内均可实现稳定收敛，因此设迭代次数itera_num=100，MCO-GA 中种群数量S=70，交叉概率为PJ=0.6，变异概率为Pm=0.07，惩罚函数中惩罚因子l1=2，l2=1.5，变异点数目为3。

表2 近岸实验仿真参数

为验证MCO-GA 在卸载方面的有效性，分析MCO-GA 在不同数据量下的收敛效果以及在降低OUE 时延方面的性能，并将MCO-GA 与以下卸载策略进行比较[4,22]。1) 基站卸载策略（简称为BSprocess 策略），总任务平均后卸载至多个基站处理，而不卸载至移动边缘节点；2) 随机卸载（简称为RANDOM 策略），各任务数据量与边缘计算节点随机分配；3) 本地执行（简称为LOCAL 策略），任务全部在本地执行，不进行卸载；4) 将文献[22]中所提的蚁群优化（ACO,ant colony optimization）应用至近岸多节点协同的卸载策略，简称为ACO 策略。

为了验证MCO-GA 能够在有限的迭代次数内实现稳定收敛，本文对MCO-GA 在不同数据量下的迭代收敛效果进行了验证。如图8 所示，随着迭代次数的逐渐增大，MCO-GA 在不同数据量下得到的时延解逐渐减小，在迭代约30 次时，可寻找到其对应情况下的最优解实现稳定收敛（部分情况在迭代100 次以内实现收敛，如数据量为1 000 kB 时，迭代约60 次实现收敛）。通过分析，可以看出MCO-GA 在不同数据量下均可实现有限迭代次数内的稳定收敛，且收敛速度较快，使算法的运算量相对较低。此外，MCO-GA 时间复杂度与其他群智能算法相比较低[11,17]，运行时间较短，可在卸载精度要求不严苛的环境下快速为OUE 找到一个可行解，具有一定的实际应用性。

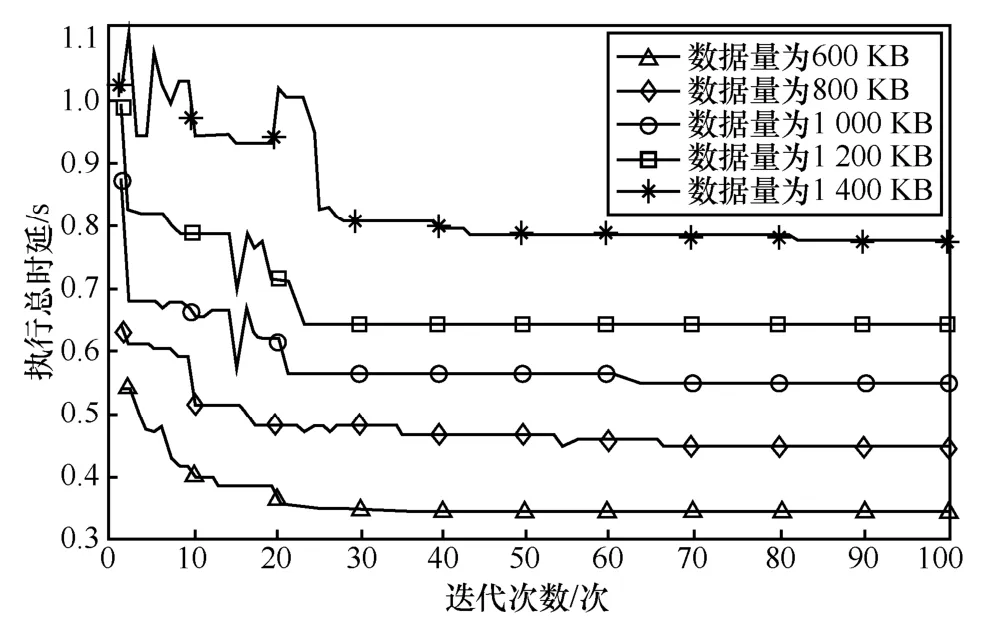
图8 MCO-GA 迭代收敛

图9 说明5 种策略执行时延总体变化趋势均随着OUE 数据量的增大而增加，但MCO-GA 策略时延增加最少。这是由于MCO-GA 结合近岸海洋特色对传统GA 进行改进，使其更加适应近岸多点协同卸载问题的寻优。而基于ACO 算法的策略由于寻优时容易陷入局部最优，其执行时延在不同数据量下均大于MCO-GA，同时证明了MCO-GA 较好的寻优效果。由于仿真设置了相同的基站与船舶数目使BSprocess 策略执行时延相对较小，若减少基站数目，BSprocess 策略执行时延会随着数据量的增加而大幅增加。由于RANDOM 策略的随机性，在不同数据量下的执行时延波动较大，数据量为1 200 KB 的执行时延明显高于1 400 KB 的情况。受OUE 本地计算能力的限制，LOCAL 策略在不同数据量下执行时延最高。通过对比可以看出，MCO-GA 在降低OUE 执行时延方面具有最好性能，在不同情况下均具有稳定收敛效果。

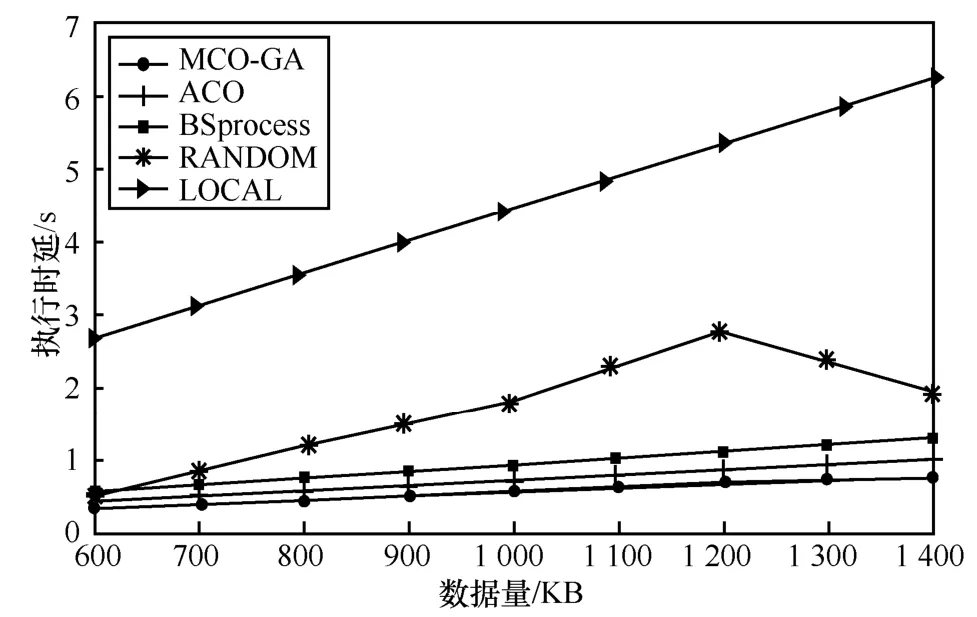
图9 不同数据量下各策略时延对比

当移动边缘节点计算能力保持不变时，随着固定边缘节点计算能力的增加，不同边缘节点计算能力所对应时延仿真结果如图10 所示（以固定数据量为800 KB 为例）。可以看出，随着固定边缘节点计算能力的提升，4 种策略任务执行时延总体均有不同程度的降低，提高了OUE 任务执行效率。MCO-GA 在不同的计算能力下均具有最小时延。再次表明所提算法随着固定边缘节点计算能力的变化可以灵活地调整卸载策略以确保系统的实时性，并且具有更好的动态适应性。

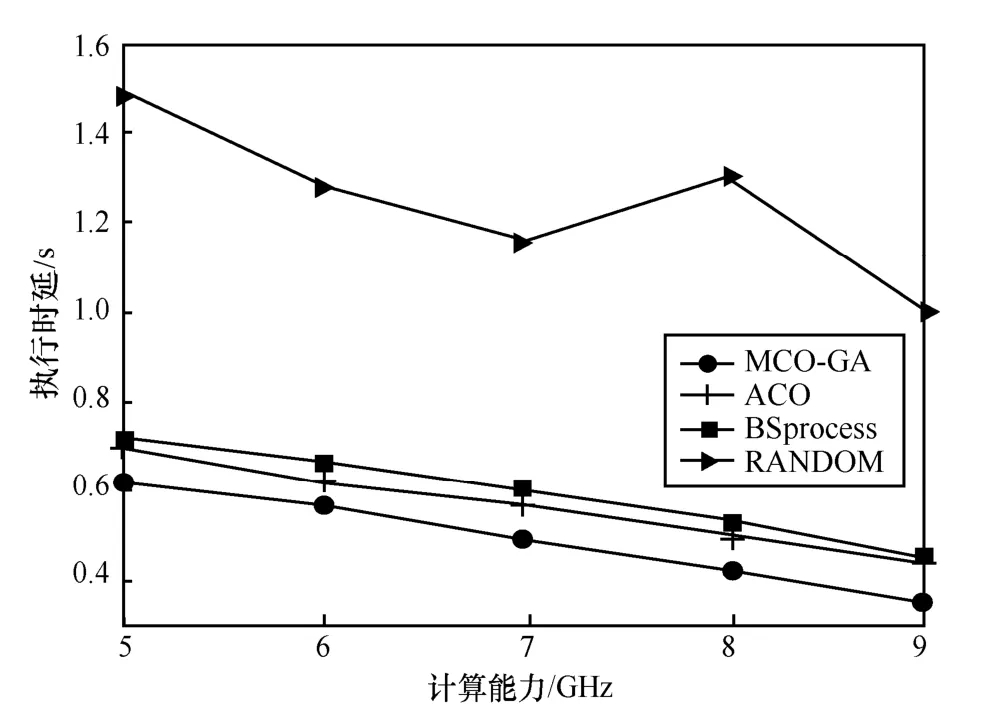
图10 不同计算能力下各策略时延对比（固定数据量为800 KB）

6.2 远岸仿真结果分析

远岸场景下模拟K个OUE 通过各自中继节点与海上基站进行卸载的网络场景，仿真参数如表3所示[4,19,23]。设置粒子数量particle_num=60，迭代次数GCL_it era=100，粒子更新速度hi取值范围为[−0.25,0.25]，惯性因子ω=0.4，随机数r1=0.4，r2=0.6。为验证基于GCL-PSO 算法的卸载策略在远岸容错机制下卸载有效性，将GCL-PSO 与以下策略进行比较。1) PSO 策略，将传统的PSO 算法应用于远岸的卸载策略；2) 平均卸载策略（简称为AVERAGE 策略），将每个OUE 的计算任务平均分配至本地，中继节点以及OBS，OBS 计算资源平均分配给K个OUE；3) 改进PSO 策略，将文献[21]中的改进PSO 算法应用于远岸卸载策略；4) 将文献[24]所提AFSA 人工鱼群算法（AFSA,artificial fish swarms algorithm）应用于远岸的卸载策略，简称为AFSA 策略。

表3 远岸实验仿真参数

为了验证基于GCL-PSO 算法的策略在解决远岸卸载问题时的寻优和收敛效果，本文将GCL-PSO策略与其他策略进行对比。如图11 所示，当OUE数量K=6且计算任务量为500～900 KB 时，基于4 种策略求得的卸载总成本随着迭代次数的增加趋于稳定，且均可在较少的迭代次数（一般为10～20 次）内实现快速收敛，运算量小。但通过对比4 种策略的寻优效果可知，GCL-PSO 策略寻优得到的系统总成本远小于其他3 种策略，这展示了该策略良好的寻优效果。综上所述，本文所提基于GCL-PSO 算法的策略在解决远岸卸载问题时可在较少的迭代次数内实现稳定收敛且寻优效果远好于其他策略。同时，GCL-PSO 策略时间复杂度为O(mn)（m和n分别代表迭代次数与粒子数目），迭代次数少，算法运算量小，说明所需运行时间较短，可满足实际应用需求。

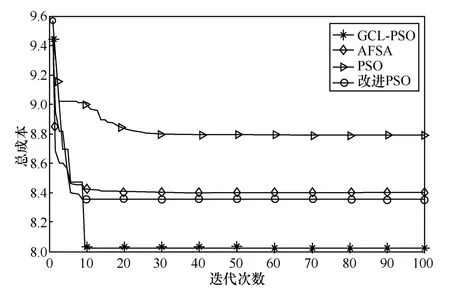
图11 算法寻优和收敛效果

本文同时对比了系统中OUE 均可正常卸载时各种算法的总成本，如图12 所示。可以发现随着系统中OUE 数量的增加，5 种策略的计算卸载系统总成本均随之增加，但GCL-PSO 的总成本较其他4 种策略增幅较小。这是由于GCL-PSO 引入了分组学习使在远岸多优化变量的复杂情况下仍能制定最优的计算卸载策略，从而降低成本。由于寻优时容易陷入局部最优，改进PSO、AFSA、PSO这3 种策略较GCL-PSO 策略相比卸载成本依次增加。随着OUE 数量的增加AVERAGE 策略系统总成本相对增加，虽然波动较小，但未实现资源的合理调配，使系统总成本较前4 种策略更大。综上所述，可以发现在正常卸载时，GCL-PSO 能够实现计算卸载最佳决策，并可高效地降低系统时延与能耗。

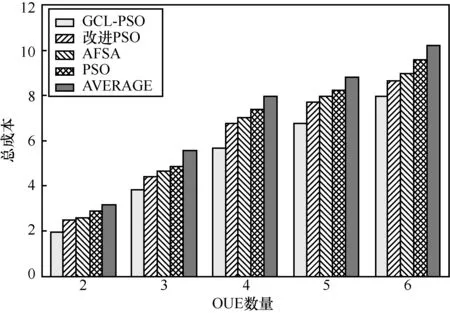
图12 正常情况下不同OUE 数量成本对比

设置系统中故障OUE 数量为1，本文对比了故障情况下不同OUE 数量的计算卸载总成本，如图13 所示。从图13 可以看出，随着OUE 数量的增加，5 种方案整体成本逐渐增加，但本文所提方案卸载总成本相对最低。同时，可以发现，当OUE 数量大于4 时，所提方案卸载成本远小于其他方案卸载成本，表明故障情况下所提方案在OUE 数量较多的系统中能有效地降低系统时延和能耗，可以很好地适应多OUE 系统中故障情况的计算卸载。综上所述，随着OUE 数量的变化，所提GCL-PSO 策略在正常与故障情况下均可实现最优卸载决策，可以很好地处理故障情况下多OUE 的计算卸载问题。

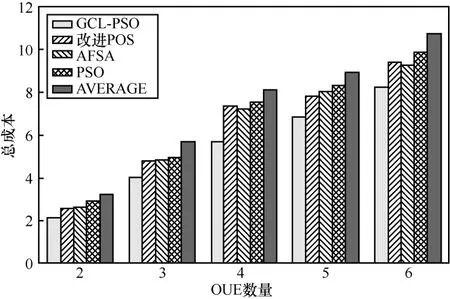
图13 故障情况下不同OUE 数量成本对比

图14 对正常情况下5 种方法在不同数据量下的卸载成本进行了分析，实验设置OUE 数量为5。从图14 可以看出，数据量的增加使5 种策略的卸载成本均有不同程度的上升，但基于GCL-PSO 策略得到的卸载成本最小，表明GCL-PSO 策略能够很好地适应不同数据量下的卸载策略寻优。此外，当数据量为500～600 KB时，GCL-PSO策略较改进PSO策略相比成本降低了20%；当数据量为600～700 KB时，GCL-PSO 策略比改进PSO 策略降低了24%的卸载成本。上述结果表明，随着数据量的增加，GCL-PSO策略在降低卸载成本方面的优势较更加明显。

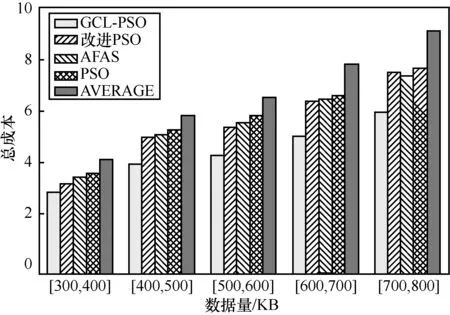
图14 正常情况下不同数据量成本对比

图15 对比了故障情况下5 种策略的总成本。实验假设OUE 数量为5，且其中一个OUE 在卸载时其对应中继和OBS 传输出现故障，需要重传卸载。对比5 种策略在不同数据范围下卸载总成本，图15说明随着OUE 任务数据量增加，5 种策略系统总成本均增加，但GCL-PSO 能在故障情况下保持较低系统成本，且系统成本增幅较小。这是由于该策略在制定正常执行时最佳卸载策略的基础上，分析并提前制定了故障情况下任务重传的卸载策略。而其他4 种策略由于在正常执行时寻优能力不够，使在此基础上的故障重传分析寻优结果不准确，成本较高。

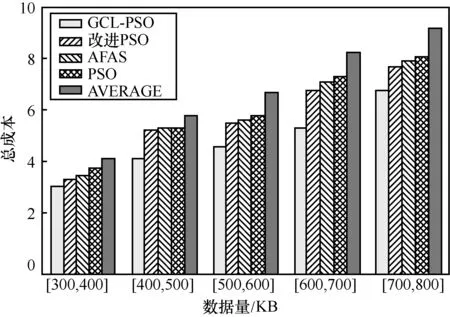
图15 故障情况下不同数量成本对比

7 结束语

本文建立了近岸与远岸2 种符合海洋特色的卸载模型。近岸场景下提出了多节点协同的卸载策略，并针对该策略提出了MCO-GA 以进一步降低OUE 卸载时延。远岸场景下提出了GCL-PSO 算法，使远岸容错卸载策略能够找到最优的卸载策略。仿真结果表明，在近岸场景下，所提算法在不同数据量下均能实现稳定收敛，且较传统方案能够极大地降低OUE 时延。在远岸场景下，GCL-PSO 算法能够实现快速收敛，与其他算法相比更加符合远岸容错机制下的卸载策略。

针对PSO 算法中局部寻优能力差和寻优片面的缺陷，GCL-PSO 算法通过引入分组竞争学习思想对PSO 算法进行了改进。仿真结果表明，GCL-PSO算法较传统PSO 算法寻优能力有较大提升。未来，将针对传统粒子群收敛精度低等缺陷对PSO 算法中的惯性因子ω等参数进行调整，可进一步提高传统PSO 算法的收敛精度。此外，将进一步分析海洋环境因素对卸载的影响，考虑融合通信资源分配因素的卸载，为更好地提升我国海洋观监测能力奠定坚实的基础。