基于网络编码的协作恢复机制线性可解性研究

殷俊，沙雪琪，王磊，张登银，杨余旺

（1.南京邮电大学江苏省宽带无线通信重点实验室，江苏 南京 210003；2.南京邮电大学物联网学院，江苏 南京 210003；3.南京理工大学计算机科学与工程学院，江苏 南京 210004）

1 引言

无线广播/多播是一种经典且高效的信息分发方式。但由于无线电波传播特性，信源传输到不同接收端的数据包具有独立删除特征，如何保证多接收方可靠接收是现代广播/多播系统设计的难点[1-2]。注意到，无线通信节点的一个典型发展趋势是多接口化，如各类智能终端、车联网车辆[3]均配置了远程通信接口和短程通信接口，基于此研究人员提出了协作恢复（CR,cooperative recovery/repair）机制。CR 通过利用相邻节点间的短程通信来恢复彼此在远程广播通信中丢失的数据包。大量实践结果表明，CR可有效地提高多播吞吐量，增强网络可靠性[4-5]。CR 在车联网中的一种典型应用场景如图1 所示，路侧单元（RSU,road side unit）需要通过广播方式向覆盖范围内的车辆广播信息。由于车辆通常会快速驶离RSU 的通信覆盖范围，因此无法持续依赖RSU 进行出错数据包的修复。考虑到不同车辆在RSU 广播阶段接收正确或出错的数据包各异，使用CR 机制的车辆在移出RSU 覆盖范围后依然可以依靠短距离通信接口互相修复彼此在RSU 广播过程中丢失的数据包。

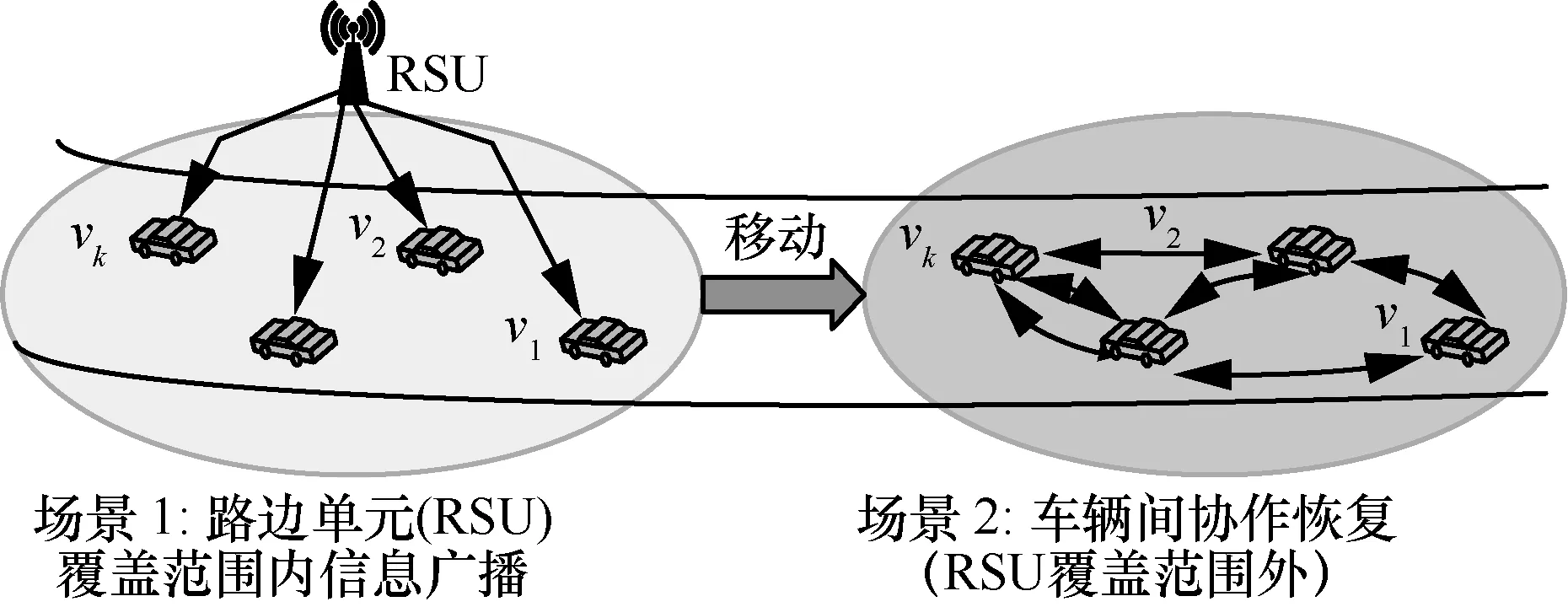
图1 CR 在车联网中的一种典型应用场景

与传统的自动重传请求（ARQ,automatic repeat request）、信源重传等可靠传输方案相比，CR 具有较明显的优势。首先，CR 降低了源节点的重传负担。其次，邻居节点之间在交互阶段使用短距离通信接口，信道质量较广播源与节点间的长程信道更高，使CR 交互过程的丢包率远小于源节点传输过程。需要指出的是，邻居节点间可以采用ad-hoc 模式进行分布式管理，因此CR 的交互过程整体控制负担较小。大量研究表明，在CR 基础上引入网络编码可以进一步提高节点协作效率[6-14]。网络编码由Ahlswede 等[15]提出，其核心思想是允许中间节点对接收到的信息进行再编码，打破了传统网络中间节点仅对信息进行存储转发的限制，可以有效提升通信网络的吞吐量和可靠性。

Park 等[6]最早提出将随机线性网络编码（RLNC,random linear network coding）[16]应用于CR 过程，协作节点需要将接收到的数据包进行随机线性组合生成多个线性无关的编码包，信宿节点收到这些编码包后进行解码，得到原始数据包。但由于RLNC在解码时需要信宿节点必须接收到足够多的编码包，因此信宿节点等待解码的时延较大。近年来，随着直连通信（D2D,device to device）的理念提出，基于网络编码的CR 机制往往与D2D 相结合[7]。Yan等[8]提出基于机会网络编码（ONC,opportunistic network coding）的CR 机制，数据包的编码组合仅依赖每个协作节点当前接收或丢失的状态。与RLNC 相比，ONC 更加灵活，节点待解码的时延更小。综合来看，当前本领域的研究主要集中在以下2 个方面。

1) 寻找更优的机会网络编码码字构造方法。其中典型的有立即可解网络编码（IDNC,instantly decodable network coding）[9-11]。由于IDNC 的编解码复杂度较低，解码过程具有及时性，因此适用于时延敏感型的近邻视频交互、实时对战游戏等应用场景。

2) 寻找更合理的节点协作传输策略，降低CR过程开销。与传统的一对多网络传输过程不同，CR在网络重传阶段的信源转变为某一个或多个网络内节点，所以协作过程的另一个重要研究内容是结合具体编码和底层传输协议寻找协作节点的内容传输策略[10-14]。文献[10]提出在D2D 网络中采用集中化方式选择IDNC 的编码包，降低单次重传的解码时延增量。在此基础上，文献[11]提出一种构造终端节点间协作传输的矛盾图算法，通过搜索极大独立集选择并行协作重传终端，降低节点间协作重传开销。文献[12]引出了节点协作过程的公平性问题。针对此问题，文献[13]将CR 过程抽象为广播和协作传输2 个阶段，并设计了一种分布式的调度算法，提高了协作传输阶段的信息恢复效率。出于同样的思想，文献[14]基于时分多址接入（TDMA,time division multiple access）协议提出了一种面向车联网的分布式CR 重传实施方法。

然而，上述2 类研究在分析和讨论节点解码时的线性可解性上均直接采用经典RLNC 方法的结论[16]。经典RLNC 线性可解性理论认为当编码有限域足够大时，只要某个目的节点成功接收到的编码包个数和源数据包个数相等就能以极高的概率解码[17]。例如，对于有限域GF(216)，当源数据包个数为5 时，接收到5 个随机线性编码数据包的目的节点解码概率超过96%。而本质上CR 编码过程是一种机会的网络编码，与RLNC 的编解码过程不可等价，直接利用RLNC 结论假设CR 协作恢复阶段目的节点收到与源数据包相同数量的编码包即可解码显然是不合理的。本文针对基于网络编码的CR 机制应用中线性可解性这一关键、基础问题展开研究，主要贡献如下。

1) 建立了基于网络编码的CR机制线性可解性分析模型；给出了不同包删除率、编码伽罗华域阶、协作节点数等多种参数综合影响下，基于网络编码的CR 机制网络内任意节点解码出所有源数据包的概率上下界。数值实验验证了该理论上、下界的准确性和紧密性。

2) 提出了一种CR 线性可解性在线判定算法。协作簇内节点可根据该算法在协作恢复过程进行编码包部分解码，不需要等待协作阶段结束。理论分析和实验表明，该算法降低了传统高斯方法的解码等待时延和存储开销。

2 系统模型

由于应用场景差异，不同研究中基于网络编码的CR 系统模型会有细微区别，本文考虑如图1 所示的典型应用场景下的两阶段CR 模型[12-13]。远程基站需要向其覆盖范围内的所有移动节点广播源信息S（不失一般性，假设S包含N个数据包并记）。采用CR 机制，S的交付过程将被分为2 个阶段。第一阶段，基站顺序广播S。由于广播信道的删除特性，网络内节点可能无法全部正确接收N个数据包。为了恢复丢失的包，相邻的节点根据地理位置或者移动特征，预先形成了若干个协作簇。第二阶段，网络编码协作恢复过程。协作簇内节点间可以通过短距离无线通信接口交换网络编码包，从而恢复彼此在第一阶段接收过程中丢失的包。假设某协作簇包含M个协作中继节点，并记为，簇内的任意节点CRi进行网络编码协作恢复的过程。若CRi第一阶段成功接收了k个源数据包，首先，CRi在有限域上随机生成前k个元素非零编码向量a={a1,a2,…,ak}；然后，进行线性编码cpi=asi产生编码结果cpi；最后，将编码结果cpi和编码向量a打包成一个编码包传递给簇内的邻居节点。

通过如图2 所示的基于网络编码的CR 系统模型详细展示上述过程。远程基站需要尽最大可能向覆盖范围内节点交付信息S={s1,s2,s3}。经过第一阶段基站广播传输后，网络内节点CR1、CR2和CR3分别接收到了部分数据包（如图2(a)所示，其中画×的数据包表示对应节点未能成功接收该数据包）。第二阶段，3 个节点形成一个协作簇，簇内采用网络编码进行丢失信息修复。CR1节点根据第一轮接收到的源数据包have1={s2,s3}，从有限域里随机生成一个编码系数向量（假设为(1,2)），根据编码向量对源数据包进行线性组合，生成一个编码包cp1=s2+2s3，并占用一个时间片传输给了邻居节点。类似地，节点CR2编码并传输了cp2=2s1+3s3。对于节点CR3，由于它侦听到了2 个编码数据包，结合在第一阶段节点收到的源数据包（也可视作以编码向量为单位向量的编码包），CR3节点共接收到3 个线性无关数据包，因此可以通过高斯消去解码出源数据包S={s1,s2,s3}，完成CR 修复过程。

通过图2 的例子可以发现，如果节点间协作传输MAC 协议采用CSMA/CA 或TDMA 协议，簇内节点在协作恢复过程同一时间片只有一个节点处于发送状态，簇内其他节点均处于接收状态可监听到该数据包（存在一定的删除率）。例如在图2 中，对于含有M（M=3）个节点的协作簇，在整个第二阶段共需要消耗M个时间片，任意节点均消耗一个时间片进行编码传输，消耗M− 1个时间片进行接收。由于采用网络编码的CR 机制工作时簇内节点间直接交互编码数据包而不是源数据包，而编码数据包是多个源数据包信息的混合，每个簇内节点只要在两阶段时间片内接收到N个线性无关编码包即可解码出所有源数据。因此，基于网络编码的CR 传输过程可自组织，减少了传统CR 过程中修复过程的时延，也避免了借助额外的控制机制所带来的资源开销。本文推导经过一轮这样的CR 传输后，簇内任意节点能够成功解码出N个源数据包的概率，这也是基于网络编码的CR 机制里一个待解决的基础问题。

图2 基于网络编码的CR 系统模型

注意到，解码过程不仅受到协作恢复的节点数量、具体网络编码有限域影响，还在很大程度上受到数据包在两阶段物理信道上传输时的删除率影响。本文采用基于文献[13,18]的具体物理信道模型建模数据包删除率：假设两阶段传输信道均为加性白高斯噪声（AWGN,additive white Gaussian noise）信道，并且各信道间独立。本文信道模型只是CR传输领域若干模型中的一种典型模型[13,18]，而基于网络编码的CR 过程线性可解性不仅受物理信道参数影响，还受到编码有限域、协作节点数等参数影响。为了保证本文结论可适应其他信道模型，后文所提出的线性可解性及其结论仅依赖于信道上传输的数据包删除率，独立于具体底层所使用的物理信道。因此，应用了其他信道模型的CR 机制容易在本文信道模型建模思路上修改使用。在基站广播阶段，簇内任意节点CRi收到的信号为

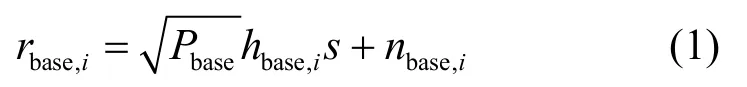
其中，Pbase表示基站传输功率；hbase,i表示基站和节点CRi间的信道增益，是一个均值为0、方差为的循环对称复高斯变量；s是基站广播的信号；nbase,i是均值为0、方差为的复AWGN 噪声。同理，在协作传输阶段，任意节点CRi接收到来自节点CRj的信号为

其中，esr表示第一阶段广播信道的删除率，erd表示第二阶段协作交互信道的删除率；Ethreshold表示预设的频谱效率门限值。据此，可以建模CR 过程，记M为协作簇的节点个数，Fq为阶为q的网络编码运算有限域，模型详细参数如表1 所示。不失一般性，从M个协作节点中任选一个节点CRi为目标节点，下面将分析经过一次完整的两阶段CR 数据传输过程之后，节点CRi能够成功解码出全部N个源数据包的概率。

表1 模型参数及其含义

3 基于网络编码的CR 线性可解性分析

根据第2 节的系统模型可知，对于包含M个节点{CR1,CR2,…,CRM}的协作簇，簇内任意节点CRi在整个CR 传输过程中可以接收的（编码）数据包有2 个来源：第一阶段广播信道上基站发送的N个源数据包和第二阶段交互信道上簇内其他邻居节点发送的M− 1个编码数据包。假设节点CRi在广播阶段成功接收了k(0≤k≤N)个数据包，其概率为Prsuc_brod(k)，由于信道传输过程独立，因此由二项分布得

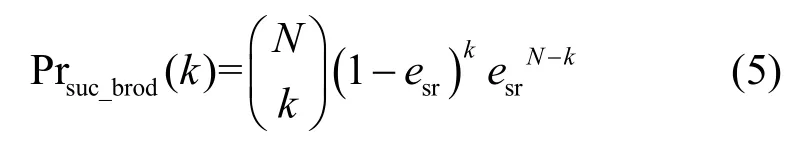
其中，esr表示广播信道的删除率。由全概率公式可得，经过一轮完整的CR 数据传输过程之后CRi成功解码出所有N个源数据包的概率Prsuc为

其中，Ek×k是k阶单位阵；QN×N是N阶初等列变换阵，可交换矩阵 (Ek×k0)列次序使(Ek×k0)QN×N=Ck×N。

示例1如图2 所示的CR 过程，节点CR3在两阶段接收的编码包CP=[s3s2+2s32s1+3s3]T及其传输矩阵按式(7)分解过程

因此，CRi在接收到CP后是否能够成功解码出所有源数据包SN问题等价于式(7)的线性方程组是否有唯一解，因此从列秩考虑解码失败的概率为

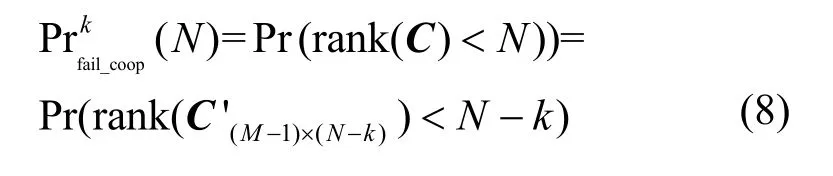
式(8)成立是因为只有传输矩阵C的秩为N时，方程组才可由CP解码出SN。考虑到rank(QN×N)=N，且 rank(Ek×k)=k，有。因此，CRi成功解码的概率可以通过判断是否列满秩来判定。为了简便，下文将简记为C'。事实上，QN×N仅交换了C的列次序，使矩阵C'各列对应的是CRi第一阶段未成功接收的N−k个数据包，并未改变C'元素值，而C'元素值在上随机分布，由两阶段传输过程共同决定。记εl表示簇内除CRi外第l(1≤l≤M−1)个节点传输到CRi节点的编码包删除率，显然 Pr{εl}=erd，。如果哑变量θ来自Fq，则C'中第l行上任意元素clj(1≤j≤N−k)的取值概率为

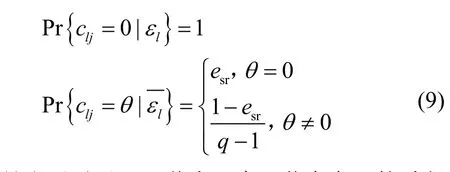
这是由于对于CRi节点而言，若在交互的过程中来自第l个节点的编码包发生删除，则矩阵C'的第l行所有元素clj(1≤j≤N−k)一定全为0；反之，则clj由第l个节点在广播过程是否接收到源数据包sj来确定元素是否为0。若2 个阶段均未发生删除，则clj值可以为q阶有限域Fq中任意一个非零元。因此，clj取到某一确定的非零元的概率为

综上，CR 可解性分析思路是由式(9)的CR 过程编码矩阵C'元素取值概率，然后根据式(8)分析C'的秩，从而求解CRi协作阶段不能成功解码出剩余N−k个数据包的概率的上下界，进而根据式(6)得到CRi解码出所有N个源数据包Prsuc的上界Pmax和下界Pmin。

4 基于网络编码的CR 线性可解性上界

与第3 节分析的场景一致，本文依旧假设簇内任意节点CRi在广播阶段仅收到N个源数据包里的k(0≤k≤N)个。根据CR 传输过程容易发现，若簇内所有节点均未能在广播阶段成功接收某一个源数据包，则通过基于网络编码的CR 过程也一定不能成功解码出这一源数据包。例如，在图2 所示例子中，若节点CR2广播阶段未能接收到源数据包s1，则簇内任意节点无法通过协作过程解码恢复出s1。因此，根据二项分布容易得到簇内任意节点CRi解码失败概率的一个简单下界为

容易发现，式(10)给出的下界仅考虑了广播阶段数据包删除率，忽略了更关键的交互阶段。因此，下面，本文将基于文献[20]的稀疏矩阵线性可解性判定思想，给出的另一个下界。

定理1在基于网络编码的CR 机制中，对于包含M个节点的协作簇，若簇内任意节点CRi在广播阶段仅收到N个源数据包里的k(0≤k≤N)个，则CRi在协作阶段不能够完全解码出其余N−k个源数据包的概率的一个下界可以表示为

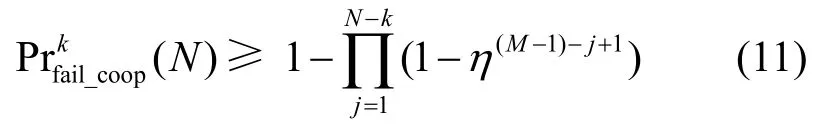
其中，η=min(erd+(1−erd)esr,(1−esr)(1−erd)/(q− 1))。

证明详见附录1。

因此，综合式(10)和定理1，即可得到的一个较紧密下界为

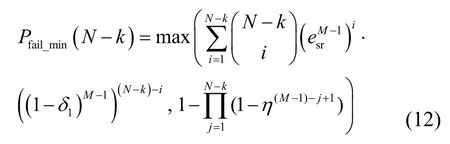
其中，η=min(erd+(1−erd)esr,(1−esr)(1−erd)/(q− 1)。由簇内任意节点CRi在广播阶段仅收到N个源数据包里的k个，且0≤k≤N，因此将式(12)代入式(6)，即可得到CRi经过一次完整的数据传输过程之后成功解码出N个数据包的概率Prsuc的一个较紧密上界Pmax为

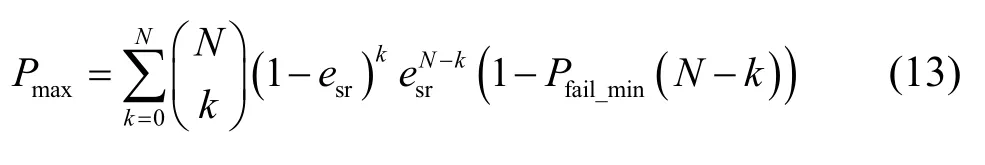
5 基于网络编码的CR 线性可解性下界

与上界分析的模型一致，本节分析CR 线性可解性的下界。

定理2在基于网络编码的CR 机制中，对于包含M个节点的协作簇，若簇内任意节点CRi在广播阶段仅收到N个源数据包里的k(0≤k≤N)个，则CRi在协作阶段不能够完全解码出其余N−k个源数据包的概率的一个上界为

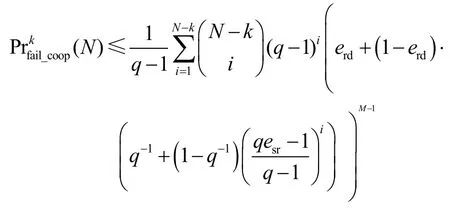
其中，esr和erd分别是两阶段的数据包删除率，q是编码有限域阶。

证明详见附录2。

实验表明，定理2 所得到的上界在编码有限域阶q的值较小时紧密；而当q较大时，其值趋近于1，失去指导价值，需要进一步优化。注意到，由定理1 的证明过程，解码失败概率的上界还可以表示为

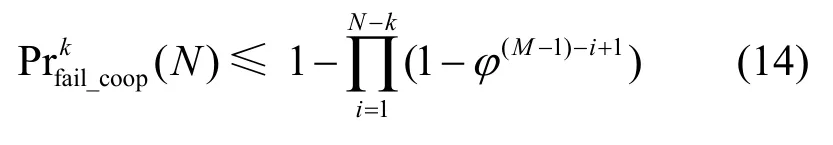
其中，ϕ=max(erd+(1−erd)esr,(1−esr)(1−erd)/(q− 1))。证明过程与定理1 相同，此处不再赘述。

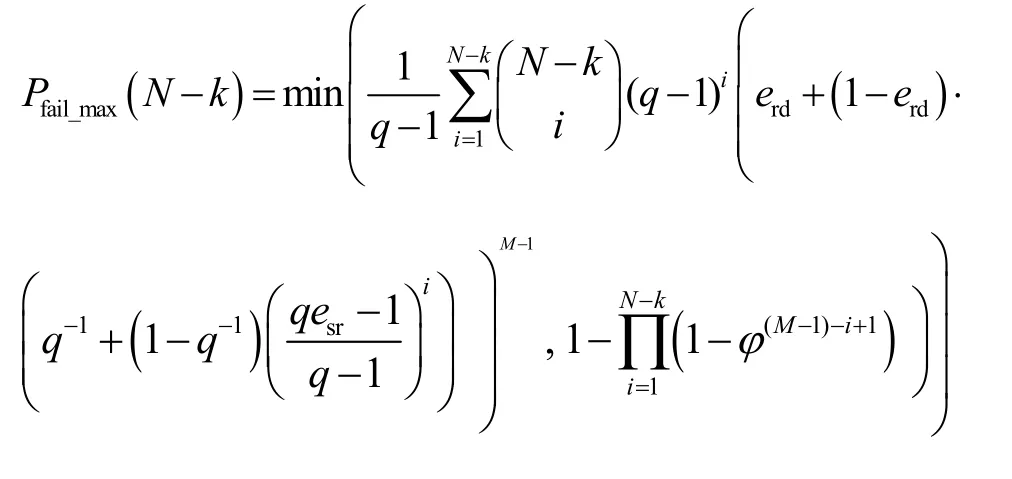
其中，ϕ=max(erd+(1−erd)esr,(1−esr)(1−erd)/(q− 1))。将上式代入式(6)，即可得到簇内任意节点CRi经过一次完整的数据传输过程之后成功解码出N个数据包的概率Prsuc的一个较紧密下界Pmin为

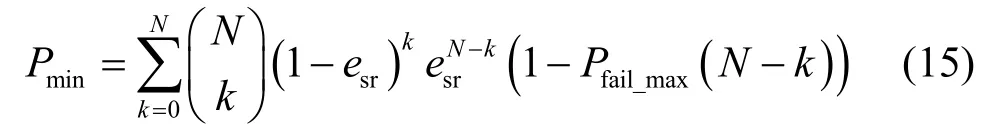
6 基于网络编码的CR 线性可解性在线判定算法设计

在已有基于网络编码的CR 研究中，簇内节点对编码数据包的解码发生在整个CR 协作恢复阶段完成之后，采用Gauss 消去法对其所有接收到的编码包进行统一解码。若能解码出所有源数据包，则说明线性可解，反之则不可解。因此，传统研究中每个簇内节点在整个协作阶段均需要侦听所有编码包，然后在协作阶段完成后统一解码，因此解码的等待时延较高，节点持续侦听引起的能耗也较高，并且节点还需要预留足够的存储空间以缓存待解码数据包。针对该问题，本文提出一种在线判定算法——改进Gauss-Jordan 法，工作流程如图3 所示，每个簇内节点能够在CR 协作恢复过程中就根据自身接收到的编码包进行部分解码，不需要等待协作阶段完成再进行，不仅降低了传统高斯方法的解码等待时延，也避免了需预设编码包缓存空间所引起的存储开销。

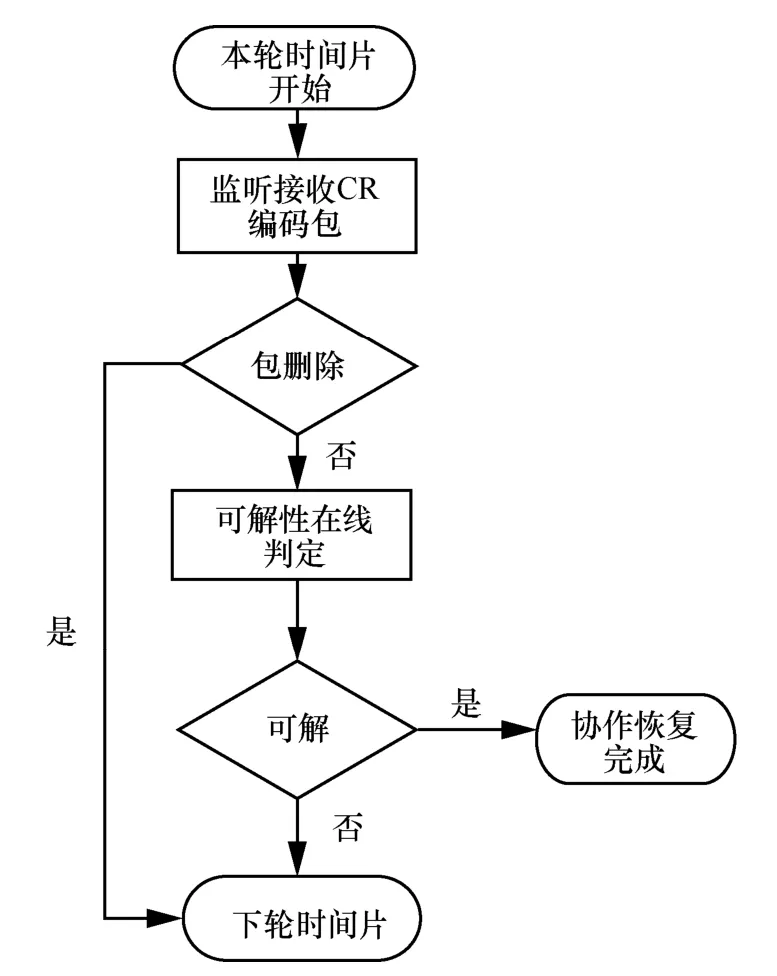
图3 改进Gauss-Jordan 法的工作流程

簇内任意节点CRi采用改进Gauss-Jordan 法的解码过程描述如算法1 所示，注意，可解性在线判定过程也是逐步解码的过程。对于图2 所示例子，采用所提算法的节点CR3在两阶段CR 过程在线解码过程如表2 所示，该过程共消耗了5 个时间片，3 个为广播阶段接收源数据包，2 个为协作修复阶段接收编码包。

表2 改进Gauss-Jordan 算法解码过程

算法1改进Gauss-Jordan 算法的CR 协作过程可解性判定与渐进解码算法

7 改进Gauss-Jordan 算法与传统Gauss 方法性能对比分析

7.1 解码时延对比分析

1) 传统Gauss 方法

在传统Gauss 方法解码过程中，协作簇内任意节点CRi在第二阶段完成后才尝试进行高斯消去解码，因此解码出源数据包的时延GaussianT就是两阶段CR 传输过程所消耗的时间，即广播阶段基站发送N个源数据包的发送（传输）时延Tbroad和协作恢复阶段的编码数据包排队待解码的时延Tcoop。为了简化分析过程，解码时延分析未考虑无线信号的传播时延和解码过程的运算处理时延。若协作簇包含M个节点，并且为了分析方便，将两阶段信道传输一个数据包或编码包的时延均记为一个时间片，则Gauss 方法CRi解码成功的时延恒定，值为TGaussian=Tbroad+Tcoop=N+M，单位为时间片。

2) 改进Gauss-Jordan 算法

与传统Gauss 方法相比，簇内任意节点CRi采用改进Gauss-Jordan 算法的时延TGauss-Jordan也包括两部分：广播阶段消耗的时间片Tbroad（Tbroad=N）和协作阶段在线解码时延。由于CRi在协作修复阶段采用所提出的改进Gauss-Jordan 算法可在线判断可解性，随着接收编码包累积的过程，一旦发现解码矩阵CP线性可解即停止侦听并完成解码。因此，CRi协作阶段解码时延是随着编码包接收过程直到解码矩阵CP满秩的平均时间。为了量化分析，本文将节点采用改进Gauss-Jordan 算法的解码过程建模为一种齐次吸收马尔可夫过程（AMP,absorbing Markov process）。

定义1在CR 协作恢复阶段，当且仅当rank(CP)=r，k≤r≤N，簇内任意节点的解码状态对应AMP 的状态sr。

改进Gauss-Jordan 算法的解码AMP 模型如图4 所示。为了合理估算簇内任意节点的平均解码时延，AMP 的初始状态设置为广播阶段完成后簇内任意节点成功接收到的数据包个数期望。因此，sk为节点协作阶段解码矩阵CP秩的初始值，且，其中∗为取整运算。AMP 的吸收态为CP满秩状态sN，因此此状态下转移概率pN,N=1。为了求解AMP 的状态转移矩阵以分析平均时延，本文接下来给出一些基础的定理。

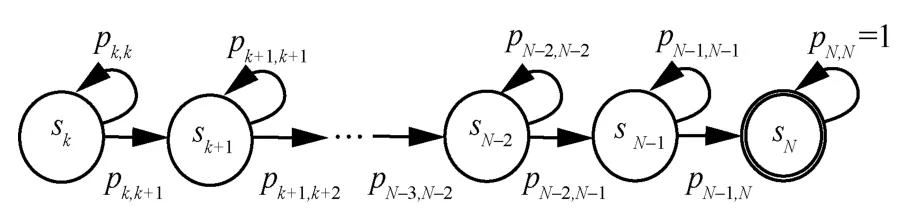
图4 改进Gauss-Jordan 算法的解码AMP 模型

引理1[20]对于一个n×n矩阵M，若其矩阵元素均从有限域GF(q)上随机选取，且选取值为0 的概率为1−p，选取GF(q)上任意非0 元的概率为p/(q−1)，则矩阵M非奇异的概率至少为其中π=max{p/(q−1),1 −p}。

证明见参考文献[20]“Theorem 6.3”。

推论 1在 CR 协作恢复阶段采用改进Gauss-Jordan 算法解码，协作簇内任意节点的解码矩阵记为CP，若某时间片编码矩阵CP秩为t，则后续时间片该节点若成功接收一个新的编码包，更新解码矩阵为CP'后，解码矩阵CP'秩增为t+1 的概率为

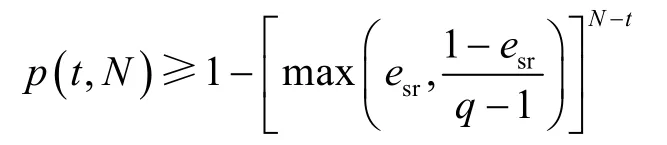
其中，esr是CR 广播阶段数据包平均删除率。

证明详见附录3。

由于寻找p(t,N)的精确解一直是数论领域的一个待解难题，尚未寻找到其解析解[21]，在下文AMP 的状态转移概率分析中，本文采用推论1 的结论来近似p(t,N)，即

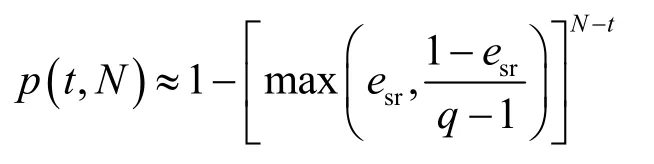
基于此，本文分析协作恢复阶段任意节点解码过程AMP 的任意两状态间的转移概率。

引理2在CR 协作恢复阶段采用Gauss-Jordan算法解码，若协作阶段编码包删除率为erd，则间隔一个时间片簇内任意节点的马尔可夫过程由当前状态si转移至状态sj的概率pi,j为

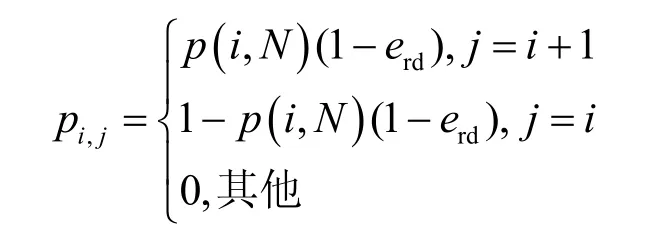
证明详见附录4。

引理2 给出了AMP 任意两状态转移概率，将它作为矩阵元素容易得到AMP 的一步状态转移概率矩阵P，按标准型[22]分块排列后形如

其中，P的第一行和第一列对应AMP 吸收态sn，其余行列按次序分别对应瞬时态sk,…,sn−1，(n−k) ×(n−k)矩阵Q为所有瞬时态间的一步转移概率矩阵。接下来，本文将根据P和吸收马尔可夫链性质估算出改进Gauss-Jordan 算法AMP 从初始态sk转移至吸收态sn的平均步数，而AMP 每移动一步均消耗一个时间片，即可得到改进Gauss-Jordan 算法的平均解码时延。

定理3M个节点在CR 协作阶段采用改进Gauss-Jordan 算法恢复N个源数据包，其在线解码过程平均时延T=(I−Q)−1，其中I为单位阵，Q为所有瞬时态间的一步转移概率矩阵。

证明详见附录5。

由于改进Gauss-Jordan 算法总时延TGauss-Jordan包括固定的广播阶段时延Tbroad(Tbroad=N)和协作阶段在线解码时延两部分，由定理3 得

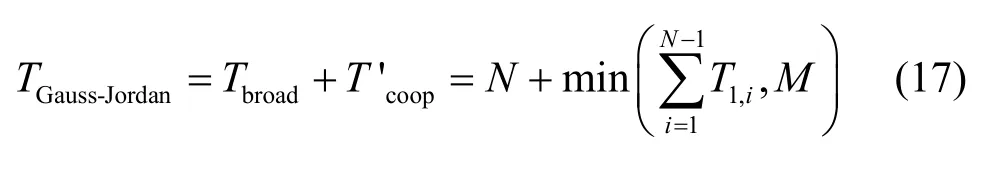
因此，在解码时延方面改进Gauss-Jordan 算法明显优于传统高斯方法（TGaussian=N+M），且只有在最坏情况即解码失败时才会等于传统高斯方法。

7.2 算法复杂度对比分析

采用传统Gauss 方法解码时，解码过程发生在两阶段CR 传输过程结束后，在解码时需将两阶段接收到的所有编码包联立方程组求解。由伯努利过程性质知，具有M个节点的协作簇，任意节点在广播阶段平均收到N个源数据包中的Nesr个，在协作恢复阶段平均收到(M−1)erd个编码包，因此基于高斯消去的 Gauss 方法的解码时间复杂度为O((esrN+erd(M−1))3)。

本文所提出的改进Gauss-Jordan 算法在协作恢复阶段，每个时间片成功接收到新的编码包后会执行一次消元处理，这样的消元处理共有（N−esrN）次。由算法1 知，协作阶段若第i次收到编码数据包，则第i次消元运算规模为(esrN+i)2次，因此改进Gauss-Jordan 算法的总时间复杂度为即与Gauss 方法对比，2 种解码方法均为多项式复杂度，但改进Gauss-Jordan 算法复杂度较小，且问题规模不受协作簇节点数影响，更适应于大范围的部署应用。

8 数值结果

本节通过数值模拟与实际部署相结合的思路来检验上文给出的结论和算法。仿真过程采用控制变量法，控制编码有限域阶数、协作节点数、源数据包数、两阶段信道删除率等多种变量参数，检验CR 过程结果并与上文结论进行对比。例如，对于解码成功率检测实验，通过实验协作网络内任意目标节点解码出所有源节点数据包的概率，再与式(13)给出的理论上界Pmax和式(15)给出的理论下界Pmin进行对比验证。为了降低误差，每组实验均运行了106次。可解性理论上下界验证实验参数设置如表3 所示。

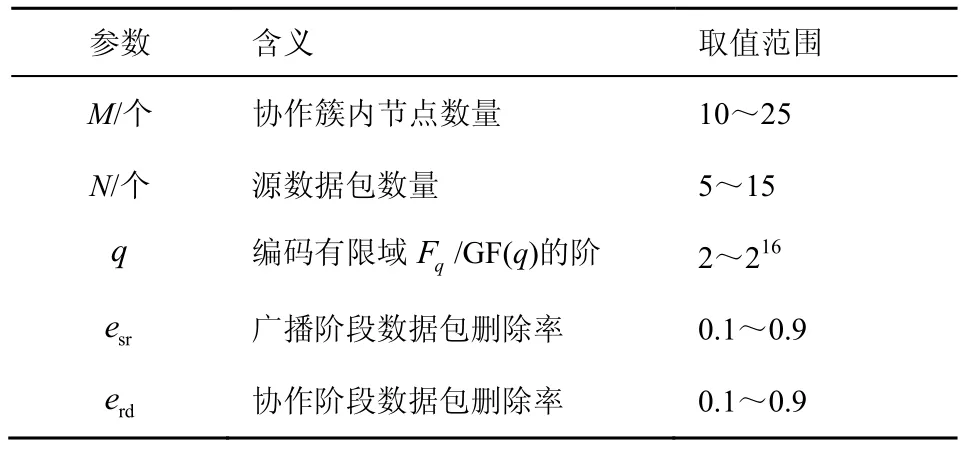
表3 可解性理论上下界验证实验参数设置

首先，实验编码有限域阶对目标节点线性可解性的影响。固定源数据包数N=10，协作节点数M=15，节点广播信道删除率esr=0.5和协作信道删除率均为erd=0.5，当编码有限域Fq阶q变化范围为2～216时，簇内节点经过CR 过程解码成功率如图5 所示。

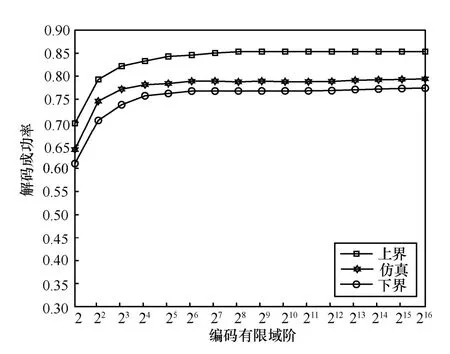
图5 编码有限域阶对解码成功率的影响

从图5 可以发现，在不同编码有限域阶下，所提出的理论上下界均有效，并且当编码有限域阶小于24时，随着有限域阶的增加，节点解码成功率迅速上升，这一趋势在编码阶处于24～28时会变缓，而当编码阶大于28时，编码有限域选择不再对线性可解性和理论上下界产生明显影响（编码有限域阶从28增加到216，但解码成功率仅从0.788增加到0.794）。这说明编码有限域阶选取过小会造成CR 机制可解性差，而当有限域阶超过一定值时就不再成为可解性的主要约束因素，因此设计具体CR 机制需要在考虑编解码效率基础上合理地选择编码有限域。

在此基础上，进一步实验所提出的改进Gauss-Jordan 算法在不同编码有限域下的渐进解码算法解码时延，实验时维持源数据包数、协作节点数、广播信道删除率均与图5 所示实验一致，实验结果如图6 所示。结果显示，在同一个编码有限域下，随着协作阶段数据包删除率增加，解码时延明显递增，最终趋近于传统Gauss 方法解码时延。这是由于随着协作删除率增加，节点的线性可解性下降直至解码失败。横向对比不同域在某一个协作信道删除率下的解码时延可以发现，编码有限域阶越小，解码时延越大，但当编码有限域阶大于28时，编码有限域阶对解码时延影响变弱，如图6 中28和216这2 种编码有限域，虽然编码有限域阶扩大了一倍，但平均解码时延仅降低了0.1，该现象说明合理提高编码有限域阶能够增加CR 机制的协作过程解码成功率，降低解码时延，但当编码有限域阶超过一定阈值时，则提升效果有限。

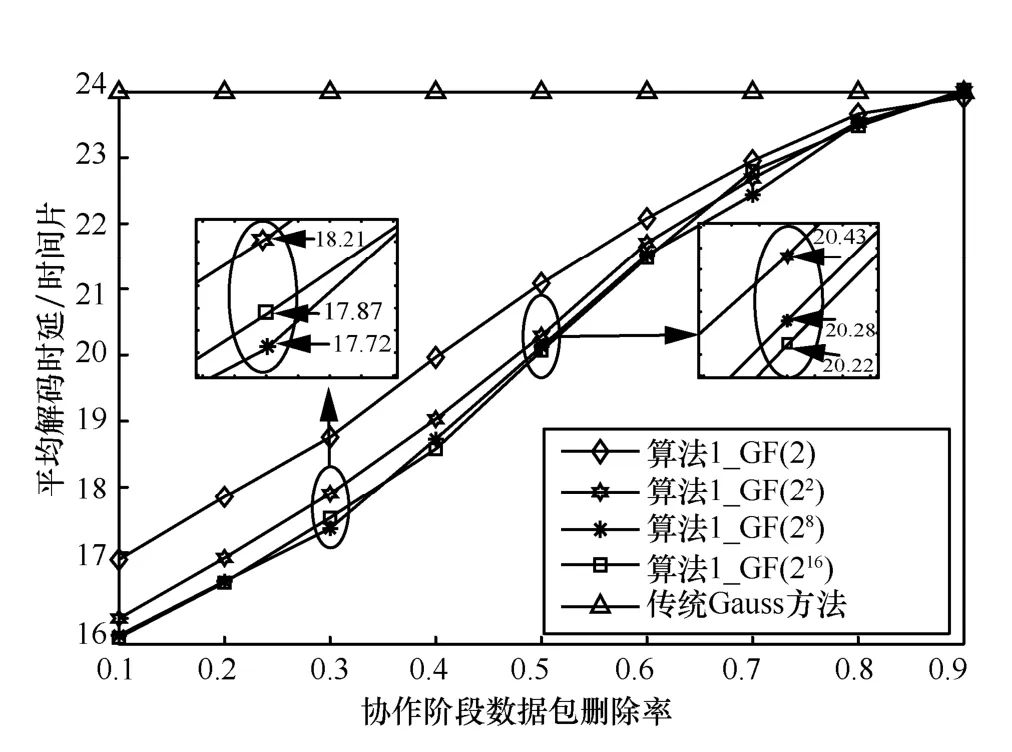
图6 改进Gauss-Jordan 算法与传统Gauss 方法解码时延比较

由7.2 节算法复杂性分析可知，2 种解码算法的复杂性主要受到源数据包数N、协作节点数M和节点广播信道删除率esr决定，而网络编码运算是基于有限域的运算，在实际节点上的运行复杂度还受到具体有限域运算实现方法影响。为了对比2 种解码算法的计算复杂度，基于一维查找表和二维查找表2 种有限域实施方法[23]分别实现了2 种解码算法，并部署在 Freescale MC13213 节点上（MC13213 是 Freescale 生产的一种基于经典HCS08 系列微程序控制器的RF 片上系统（SiP），在WPAN、ZigBee 等各类无线组网应用领域得到广泛使用）。实验时关闭了节点天线，并通过随机函数来模拟CR 过程中是否成功接收到编码数据包（对天线的收发处理需要处理器的介入，而解码算法复杂度本身与天线编码包接收过程独立。因此，不关闭天线会造成算法复杂度测试结果不准确），具体实验参数设置如表4 所示。在节点上共执行了4 组对比实验，每次实验均编码32 KB的随机数据，每组实验重复106次，实验结果如图7 所示。

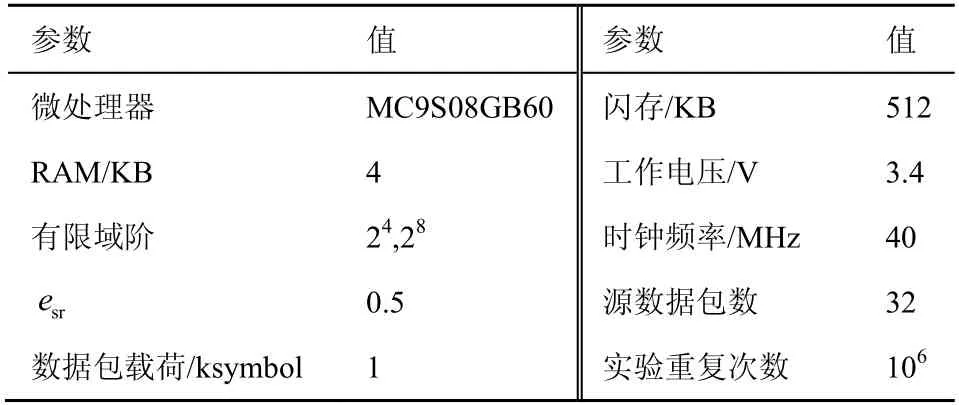
表4 改进Gauss-Jordan 算法复杂度实验参数设置

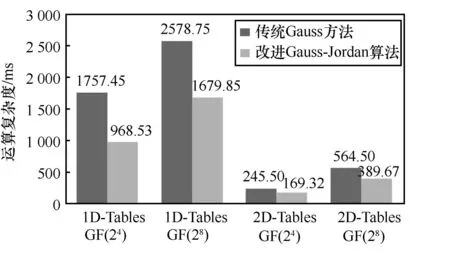
图7 改进Gauss-Jordan 算法与传统Gauss 方法运算复杂度比较

实验结果表明，在2 种有限域实现方法上本文所提出的改进Gauss-Jordan 算法均较传统Gauss 方法复杂度低约35%，这是因为改进算法的消元迭代次数较少。同时也能发现，有限域阶对2 种解码算法的复杂度影响较明显，这是因为有限域阶对有限域运算方法的RAM 存储需求差异显著。对于一维查表法，在24阶有限域上共需要设置96 B 的指数表和对数表，而28域则需要4 160 B；同样，对于二维查表法，在24阶域上共需要设置528 B 的指数表和乘、除法表，而28域需要超过128 KB 闪存空间。相较于有限域的一维查表实现法，2 种解码算法在二维查表法下运算效率提升显著，但二维表法的RAM存储需求较高，尤其是对于需要高阶有限域的CR协作过程，本质上来说，有限域的二维查表实现就是一种以存储空间来换取运算效率的方法。

接下来，本文仿真实验广播阶段数据包删除率对目标节点线性可解性的影响。设置广播信道的删除率esr变化范围为0.1～0.9、编码有限域固定为GF(24)、交互阶段数据包的删除率固定为erd=0.4，当源数据包个数N=10、协作节点数M=15时，实验结果如图8 所示。从实验网络内节点解码成功率对比上，仿真结果曲线落在下界曲线和上界曲线之间，并且更逼近下界。例如在编码有限域为GF(24)的情况下，理论下界与实际结果误差区间仅为0.83%。统计发现，上界平均误差区间为19.46%，在首尾端较紧密。这是由于随着广播信道删除率增加，当esr超过0.35 时协作节点的编码向量稀疏度会急速增大，引起由定理1 作用的理论上界松弛度扩大，这一过程会持续到esr=0.7 时，此时理论上界会切换到由式(10)所形成的约束，紧密度会得到提高。

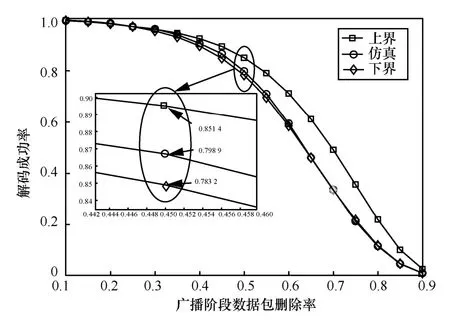
图8 广播阶段数据包删除率对目标节点线性可解性的影响

最后，分析源数据包数和协作簇内节点数对线性可解性上下界影响。固定广播信道删除率固定为esr=0.7，协作信道删除率固定为erd=0.4，编码有限域为GF(24)，分别考察源数据包数N为5～15、协作簇内节点数M为10～25 时的解码成功率，实验结果分别如图9 和图10 所示。实验发现，本文所提出的改进Gauss-Jordan 算法的上下界在不同源数据包数、协作簇内节点数下均能够较精确地估算解码成功率，并且当CR 机制各性能参数固定时，源数据包数和协作节点数对线性解码率影响较大，说明传输策略和节点协作簇建立策略是CR 机制的重要内容。同时实验也验证了一个直观结论，即在相同的信道条件下，中继节点数越大，节点的解码成功率越大；源数据包数越小，节点的解码成功率越大。

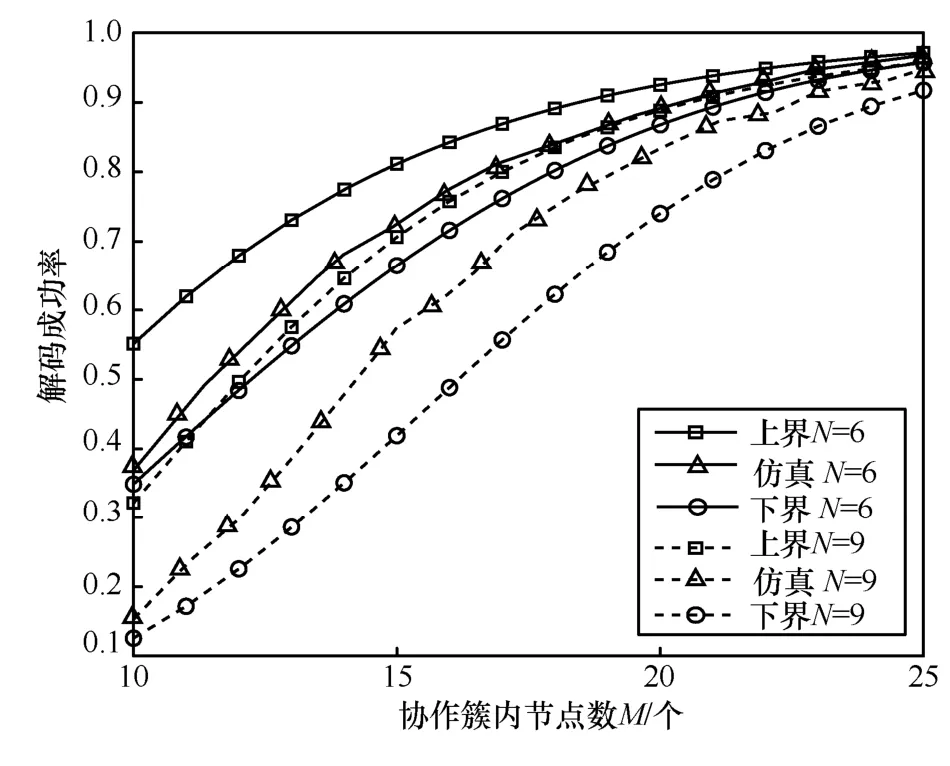
图9 协作节点数对线性可解性的影响

9 结束语

线性可解性是基于网络编码的CR 机制应用中的关键基础问题，本文建立了CR 可解性的量化分析模型，并给出了紧密的理论上下界。在此基础上设计了一种在线判定算法，降低了节点可解性识别的等待时延。下一步的工作可分成两个方向：一方面继续探索线性可解性精确解，鉴于该问题求解难度和稀疏随机矩阵的线性可解性探索等效，是数论领域待解难题，一个可行的解决思路是利用蒙特卡洛方法使用计算机实验出一个精确解再寻求理论验证；另一方向是基于本文所提出的理论上下界和渐进解码算法，设计流式协作恢复机制，实现广播和恢复两阶段的流水线联动，完成数据包的数据的在线编码传输功能，进一步在提高网络传输可靠性的同时降低CR 恢复时延。

附录1 定理1的证明

证明根据式(8)知因此可以通过判断(M− 1) ×(N−k)矩阵C'所有列向量是否均线性无关来估算界。若假设C'的前j(j=1,2,…,N−k−1)个列向量c1,c2,…,cj已被证明线性独立，则当且仅当cj+1不在这些向量所张成的线性子空间Vj中时，第j+1个列向量cj+1与这些向量线性无关。记其概率为pj+1，则根据增量思想C'的所有N−k个列向量均线性无关的概率可表示为因此问题关键在于求解pj+1。

考虑C'中前j个列向量c1,c2,…,cj形成的矩阵，由于这j个列向量线性无关，因此可以通过矩阵的初等列变换，类似高斯消去，形成存在j×j单位阵的变换阵。不失一般性，本文假设C'前j行形成了新阵的单位阵。因为初等列变换不改变空间的基，所以新阵的列向量张成的线性子空间与原空间Vj相同。由于新阵的列向量构成了子空间Vj的一组基，因此容易发现属于子空间的所有向量前j个系数可以任意取值，而其余(M− 1)−j个系数取值由前j个系数唯一确立。又由式(9)知C'里任意元素取域Fq中0 元的概率为erd+(1−erd)esr，且任意一个非0 元概率为(1−esr)(1−erd)/(q− 1)，因此向量cj+1落在Vj里的概率pj+1至多为1−η(M−1)−j，从而定理1 得证。

附录2 定理2的证明

证明由式(8)可知

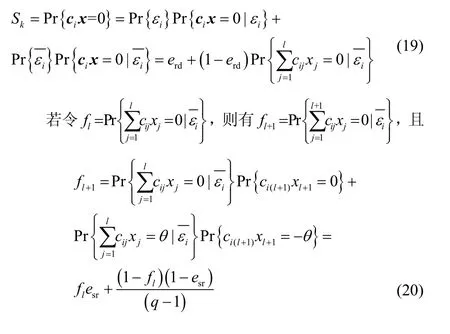
其中，θ≠ 0(θ∈Fq)。从式(20)可以整理得

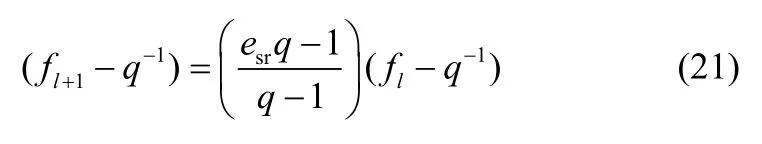
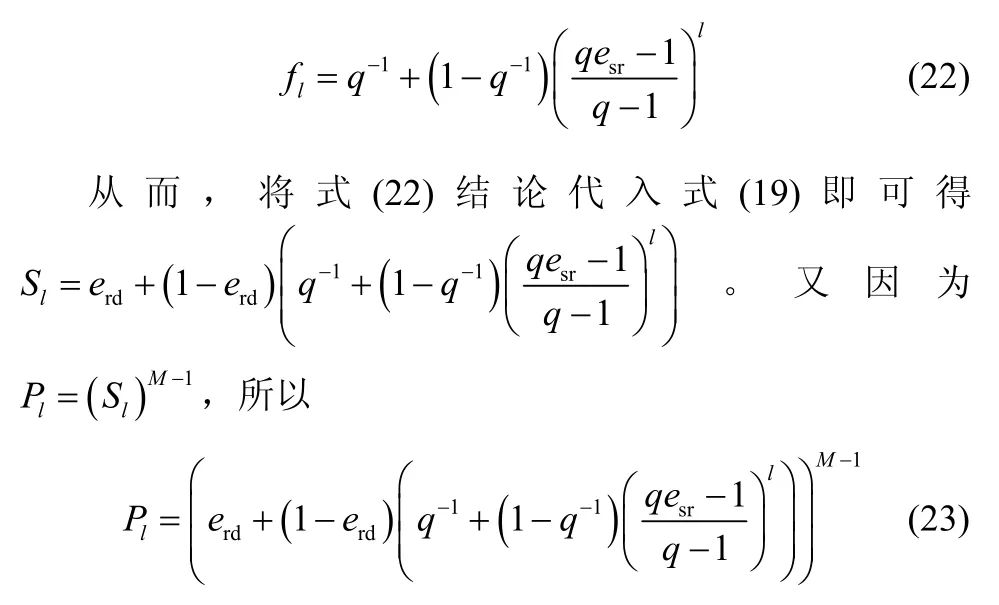
将式(23)代入式(18)，定理2 即可得证。

附录3 推论1 的证明

证明由式(9)知，在协作恢复阶段，任意簇内节点成功接收到的编码包编码系数是一个1×N维的稀疏向量，该向量的稀疏度即为广播阶段数据包删除率esr。当簇内节点成功接收到一个新编码包后，解码矩阵秩由t增加为t+1，这一过程等价于新接收的编码包编码系数向量c与由原秩为t解码阵CP的行向量所组成的向量组线性无关。根据算法1 可知，秩为t的解码阵CP共含t行向量且呈行阶梯型分布，因此当c与CP阶梯对应的前t个元素值确立后，稀疏随机向量c与CP是否线性相关取决于剩余的N−t个元素，且线性相关时的解取值唯一，代入引理1，推论1 即可得证。

附录4 引理2的证明

证明若簇内任意节点CRi在当前时间片末（假设为t）的解码矩阵秩为i（此时对应图4 所示的解码过程吸收马尔可夫链应处于si状态），则在第t+1 时间片末CRi的解码矩阵秩只可能出现2 种情况。

情况1秩增1 变为i+1。这种情况发生的条件是CRi在t+1 时间片成功接收到一个编码包，并且该编码包的编码系数向量与原解码矩阵线性无关，此时AMP 由si转移至状态si+1，因此这种情况的转移概率pi,i+1=(1−erd)p(i,N)。

情况2秩维持i不变。这种情况发生有2 种可能，一种是CRi在t+1 时间片未能成功侦听到一个编码包，即发生了删除；另一种是成功接收到编码包但是编码系数与已有编码矩阵线性相关，因此这种情况的转移概率pi,i=erd+(1−erd) (1−p(i,N))=1 − (1−erd)p(i,N)，引理2 得证。

附录5 定理3 的证明

证明由M个节点组成的 CR 协作簇采用改进Gauss-Jordan 算法恢复N个源数据包，其成功解码过程包括2 种情况。

情况1由于CR 协作恢复阶段总时长只有M个时间片，改进Gauss-Jordan 算法需在此时间片内判定解码矩阵是否可解，超过M则终止算法，因此解码时延

情况2对任意吸收马尔可夫链AMP 从瞬时态si出发至吸收态时经过瞬态sj的平均次数Yij为

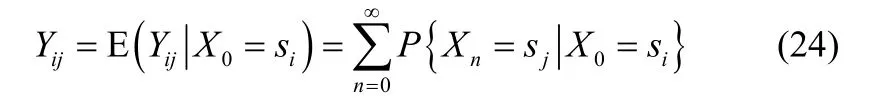
若记任意AMP 瞬时状态转移矩阵为Q，由式(24)得Yij是联合矩阵I+Q+Q2+Q3+…的(i,j)元素，又

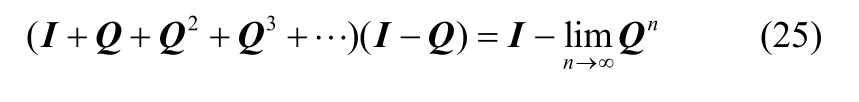
根据瞬时态转移特性知，当n→∞时任意AMP 的n步转移概率阵极限，因此I+Q+Q2+Q3+…=(I−Q)−1，即Yij是(I−Q)−1的(i,j)元素，若记T=(I−Q)−1，则Yij=Tij。

记Si表示任意AMP 从瞬时态si到达吸收态的平均步数，Sij表示到达吸收态前经过瞬时态sj的次数，则