分数阶RLαCβ电路阻抗函数含分数阶耦合电感的W域无源综合方法
梁贵书, 桑雨柔, 李天文
(1.华北电力大学 电气与电子工程学院,河北 保定 071003; 2.国网重庆市电力公司,重庆 400015)
0 引 言
分数阶微积分几乎和整数阶微积分同时出现,但直到近些年,人们才发现其相较于整数阶微积分能够更好地描述自然科学及工程领域中的一些现象。在传统电路中引入分数阶元件,便可得到分数阶电路。一方面,分数阶电路模型可作为实际分数阶电路的抽象,用于设计分数阶滤波器[1]、分数阶振荡器[2],分数阶参数可为电路的设计提供额外的自由度;另一方面,分数阶电路模型可被应用于电力电子系统及生物系统:如在电气电子系统中建立超级电容器[3]]、燃料电池[4]、锂电池的模型[5],在生物系统中建立的用于表征生物组织的Cole阻抗模型[6]、电极-组织界面模型[7]及分数阶呼吸模型[8]等等。目前对于分数阶电路的研究包含分数阶电路分析和分数阶电路综合,电路的设计及实现需要以电路综合的理论为基础,因此对分数阶电路综合的研究十分有必要。
目前分数阶电路综合理论尚未有统一的方法,但可以通过分类研究,对部分类型的阻抗函数进行综合实现。对于类型简单的分数阶阻抗函数,可以直接在s域中研究,文献[9,10]讨论了由分数阶元件及整数阶RLC元件组成的网络,其阻抗函数实现的条件,文献[11,12]讨论了分数阶双二次型阻抗函数由一个纯电阻三口网络端接两个分数阶元件的实现问题。当分数阶阻抗函数的形式较为复杂时,可通过变量代换将分数阶阻抗函数变为多变量阻抗函数,或者通过s-W变换,在W域中进行研究。文献[13]将经典的Darlington综合方法拓展至双变量的情形,并基于双变量综合方法和变量替换,提出了双元次分数阶阻抗函数的综合方法。文献[14]基于文献[13]的基础上,提出了三变量阻抗函数的Darlington综合方法。上述在多变量域中分数阶阻抗函数综合方法需要用到多口变压器及回转器,为电路的实现增加了难度。s-W变换可用于分数阶电路的研究,通过该变换可将s域中的分数阶阶次变为W域中的整数阶阶次。文献[15,16]在W域中对分数阶RLβCα电路的瞬态过程进行了分析。分数阶阻抗函数在W域中的综合方法研究目前成果不多,文献[17]基于s-W变换,研究了W域中阻抗函数的正实性,并得到了正实性等价判据。文献[19]对文献[17]中的正实性等价判据进行了改进,并研究了分数阶LαCβ两种元件电路对应的导抗函数在W中的考尔综合法和福斯特综合法。
分数阶RLαCβ电路阻抗函数可先通过阻抗换标,然后通过双变量电抗函数的综合方法进行实现,但该方法综合得到的电路含有多口变压器,且综合过程较为复杂。基于此,本文通过s-W变换,首先研究了分数阶RLαCβ电路阻抗函数在W域中能够无源综合的充分条件,接着提出了这类阻抗函数的一般综合方法,综合的电路以分数阶耦合电感替代了多口变压器,便于实际电路模型的搭建,且与以往的方法相比综合过程较为简便。文章最后通过实例对提出的综合方法进行了验证。
1 分数阶RLαCβ阻抗函数W域无源实现条件及综合步骤
1.1 分数阶元件
分数阶电路由分数阶元件和整数阶元件构成。目前较为常见的分数阶元件有分数阶电容[21]、分数阶电感[22]、分数阶耦合电感[23],下面对这些元件的特性作简要的说明。
(1)分数阶电容
分数阶电容在时域的伏安关系为
(1)
式中:β表示无源分数阶电容的元次,β∈0,1,Cβ表示分数阶电容的值,F/s1-β,分数阶电容的符号如图1所示。

图1 分数阶电容符号Fig.1 Symbol of fractional capacitance
分数阶电容对应的s域阻抗为
(2)
对式(2)作s-W变换[17],设α=nα/m,令w=s1/m,那么可得到分数阶电容W域的阻抗为
(3)
(2)分数阶电感
分数阶电感在时域的伏安关系为
(4)
式中:α表示分数阶电感的阶次,Lα表示分数阶电感的值,H/s1-α,分数阶电感的符号如图2所示。

图2 分数阶电感符号Fig.2 Symbol of fractional inductor
分数阶电感对应的s域阻抗为
ZLαs=sαLα
(5)
分数阶电感在W域中的阻抗为
ZLαw=wnαLα
(6)
(3)分数阶耦合电感
分数阶耦合电感的特性方程为
(7)
式中:L11,L22为分数阶耦合电感的伪自感值;M12,M21为分数阶耦合电感的伪互感值;α,β为分数阶耦合电感伪自感的元次;γ1,γ2为分数阶耦合电感伪互感的元次。分数阶耦合电感的符号如图3所示。

图3 分数阶耦合电感符号Fig.3 Symbol of fractional coupled inductance
分数阶耦合电感对应在s域中的阻抗矩阵为
(8)
分数阶耦合电感在W域中的阻抗矩阵为
(9)
1.2 W域中分数阶双元次线性阻抗函数
双元次线性分数阶阻抗函数在W域的表达式为[19]
(10)
式中:ηi=mci/di=mαi,i=1,2,其中α1,α2分别表示分数阶元件的两个阶次;n1,n2表示不同阶次元件的个数;al1,l2,bl1,l2,c,d为实常数。
分数阶RLαCβ电路阻抗函数可作为双元次分数阶阻抗函数的特殊情况,阻抗函数的表达式相似。根据布隆的推导[20],在整数阶电路中若阻抗(导纳)函数正实和无源性等价。在分数阶电路中,经过变量替换w=s1/m后,阻抗函数在θW≤π/2m内正实和能以梯形电路的形式无源综合不再等价,下面将举例说明。
例1 考虑如下的分数阶阻抗函数
(11)
将式(11)的阻抗函数表达式作s-W变换,得到W域的阻抗函数表达式如式(12)所示,其中m=2
(12)
令w=rejθ,其中θ≤π/4,在Matlab中作式(12)所示的复变函数的图像如图4所示,其中实部的值由z轴表示,虚部的值由三维图的颜色表示。

图4 式(12)的阻抗函数图Fig.4 Impedance function diagram of equation (12)
由该图可见,阻抗函数Zw在θ≤π/4内正实。
对该阻抗函数在W域中以梯形电路进行综合,得到如图5所示的电路图,该电路图包含元件值为-1的电感,因此无法无源综合。

图5 由式(11)得到的综合电路图Fig.5 Circuit of impedance function expressed by formula (11)
1.3 无源综合的充分条件
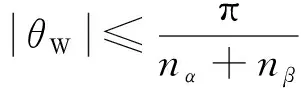
定理1的证明过程见附录。
W域中对分数阶RLαCβ电路阻抗函数综合可遵循以下步骤:
(1)对分数阶RLαCβ电路阻抗函数Zs作s-W变换,得到W域的阻抗函数Zw。
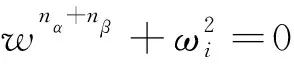
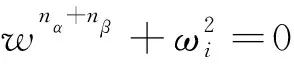
(4)计算余函数Z2w在w=τ′+jω其中τ′=tanπ/nα+nβ-1处的实部与虚部,移去部分实部的最小值Rmin,使得余下的实部与虚部在w=τ′+jω处满足Zr=Zicotnαπ/nα+nβ,移去的Rmin作为电阻串联在电路中。重复步骤(2)和(3),检验新的余函数的零极点。由于阻抗函数满足定理1中的充分条件,因此移去Rmin后余函数正实。
2 最小函数的综合
2.1 RLαCβ电路W域最小函数
分数阶RLαCβ电路阻抗函数在W域中有如下的最小函数的概念。
定义1 对于W域的RLαCβ电路的导抗函数Zw来说,若满足以下条件,那么将Zw称之为最小函数。
(1)Zw在原点和无穷远处不存在零极点;
(2)Zw在wnα+nβ+ω2=0的解对应的轴上不存在完备零极点;
(3)Rmin=Zr-Zicotnαπ/nα+nβ在轴π/nα+nβ上的某一频率ω0处取得最小值为0;
其中Zr与Zi分别表示Zτ′+jω的实部与虚部,τ′=tanπ/nα+nβ-1。nα、nβ为分数阶电感与电容在W域的阶次。
2.2 RLαCβ电路W域最小函数的布隆综合法
当阻抗函数无法再通过1.3节提取零极点的方式进行综合时,可通过构造最小函数的方法对其进行综合。令L1=Zτ′+jω0/τ′+jω0nα,并分为L1>0和L1<0两种情况来讨论,本文以L1>0为例,综合的步骤如下。
(1)提取负值电感,提取的分数阶电感元件值为L1=Zτ′+jω0/τ′+jω0nα,并将其串联在电路中。提取分数阶电感后,余函数为Z1w=Zw-L1wnα,由于Zw正实,且L1<0。故余函数Z1w正实。
(2)消去Z1w在w=τ′+jω0处的零点,余阻抗函数Z1w在w=τ′+jω0处存在零点,因此对应的余导纳函数Y1w在w=τ′+jω0处存在极点,即余导纳函数可被分解为以下形式
(13)

(3)消去Z2w在无穷远处的极点,由于Z1w在w→∞处存在极点,因此Y1w在w→∞处存在零点,根据式(13),当w→∞时,Y2w→0,因此Z2w=1/Y2w在w→∞处有极点,可将这一极点提取,电路综合为串联电感L3,余函数
Z3w=Z2w-L3wnα
(14)
电感L3为正,且余阻抗函数Z3w正实,阻抗函数的电路实现如图6(a)所示,图6(a)所示的电路可等效为图6(b),此时负值电感被消除,图6(a)和图6(b)元件值的对应关系为L11=L1+L2,L22=L2+L3,M=L2。
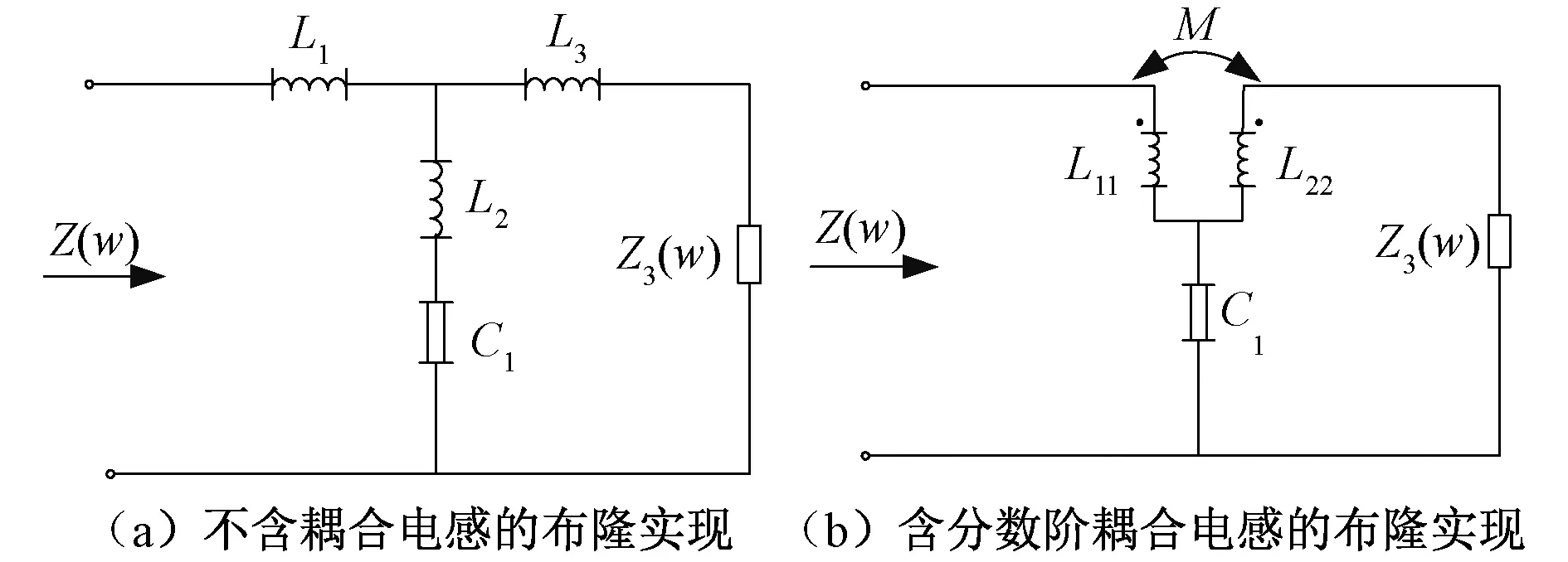
图6 L1>0时的布隆实现Fig.6 Brune realization when L1>0
图6中由电感和电容构成的二端口网络称为一个布隆节,当L1<0时,综合的过程与L1>0的情况成对偶关系,综合得到的一个布隆节如图7(a)所示,图7(a)所示的电路等效为图7(b),进而可以等效为图6(b)所示的含分数阶耦合电感的二端口网络。对阻抗函数布隆循环综合即可得到最终的电路图。
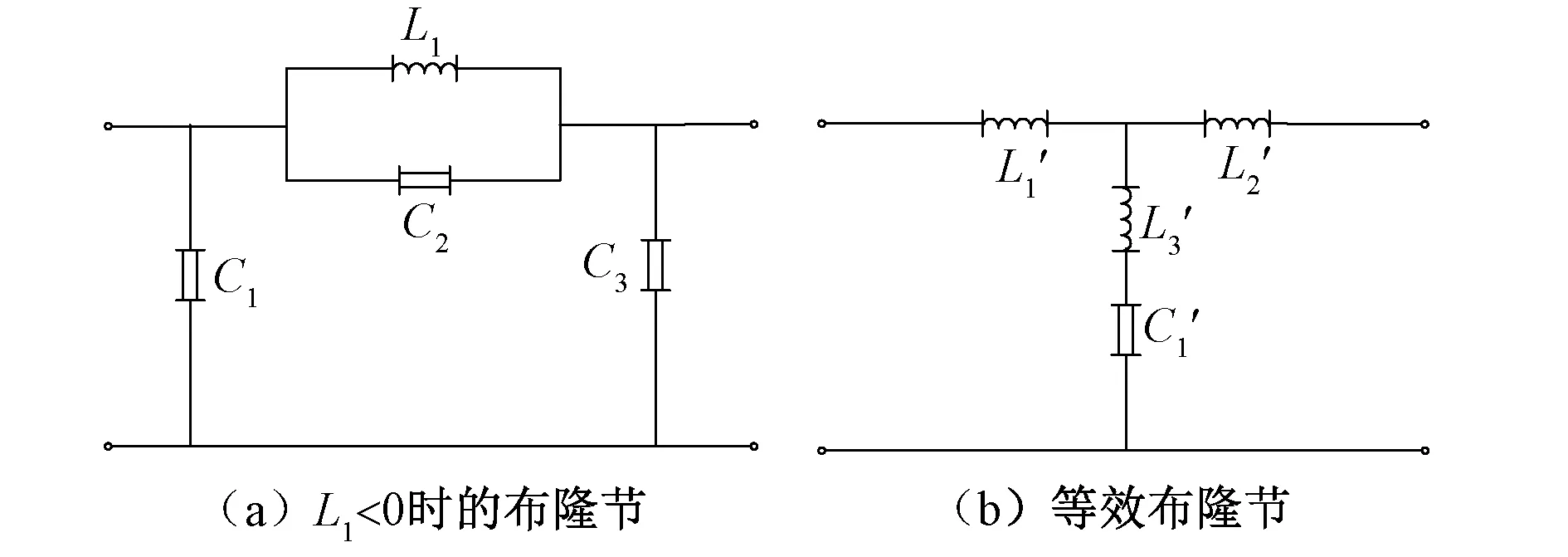
图7 L1<0时的布隆节Fig.7 Brune section when L1<0
3 综合示例
例2 综合含RLαCβ元件的分数阶阻抗函数如式(15)所示
(15)
令m=20,可得nα=m·α=14,nβ=m·β=7,得到阻抗函数Zs在W域中的表达式为
(16)

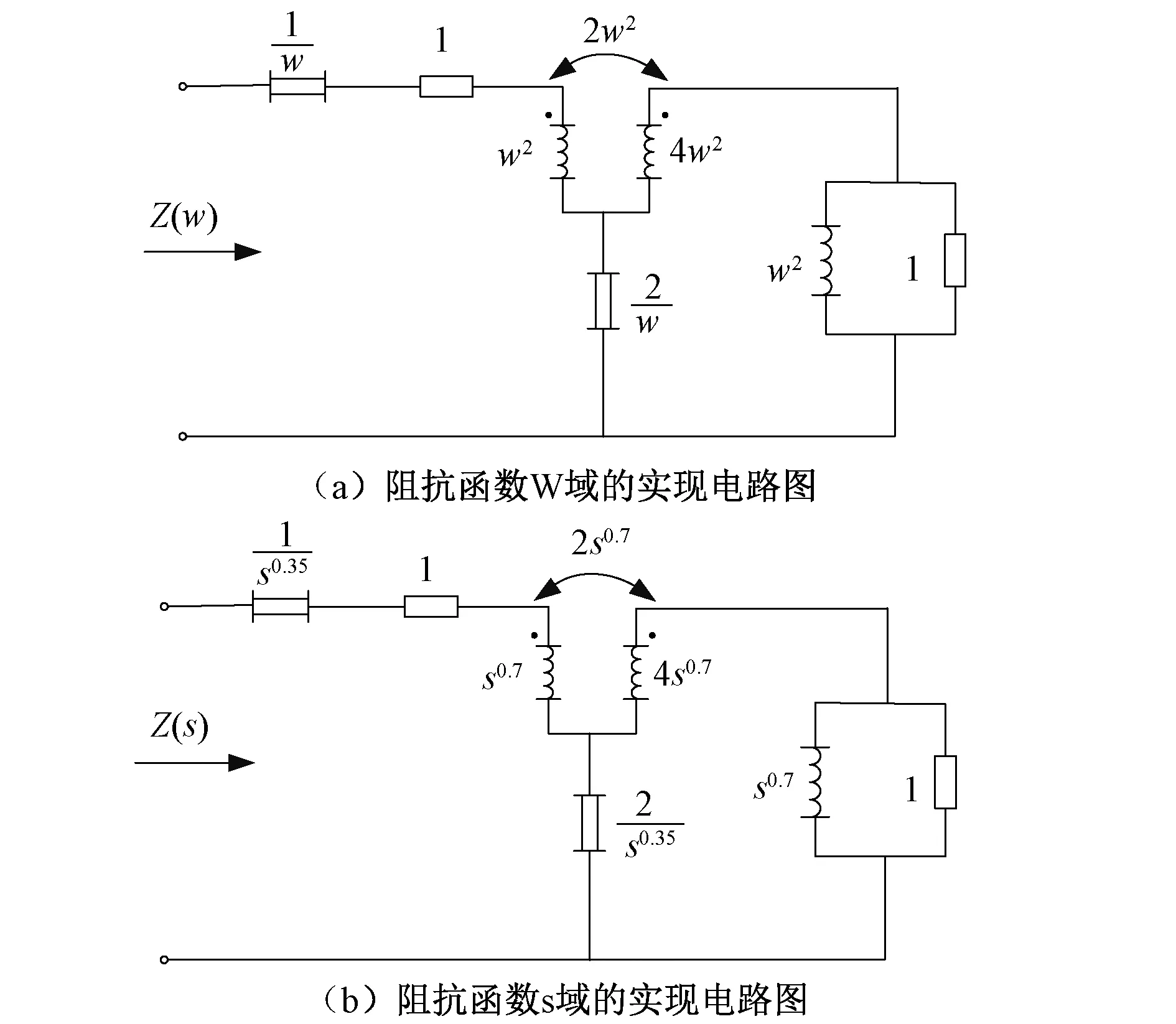
图8 阻抗函数的电路图Fig.8 Circuit of impedance function
对图8所示的电路分别施加图9所示的正弦稳态电流和暂态电流,得到数学计算和电路仿真的情况下得到的端口电压响应如图10所示,对比发现,两者的结果一致,说明用本文的方法得到的综合电路图正确。

图9 电流激励Fig.9 Current excitation

图10 端口电压响应Fig.10 Port voltage response
4 结 论
分数阶电路相较于整数阶电路增加了电路设计的自由度,分数阶电路综合理论不仅可以用于设计分数阶滤波器、分数阶振荡器等,还可以在其他工程领域建立相应的分数阶电路模型。
本文研究了RLαCβ电路阻抗函数无源综合的充分条件,给出了RLαCβ电路W域最小函数的定义并提出了最小函数的布隆综合法,并通过实例验证了方法的有效性。本文给出的综合方法与以往的综合方法相比,综合的电路无需多口变压器和回转器,综合过程更加简便。本文的研究内容丰富了分数阶阻抗函数无源综合的理论,并为后续分数阶电路综合方法的研究做出了铺垫。

