基于自抗扰控制的风电并网系统广域阻尼协调控制

梁纪峰， 马燕峰， 霍亚欣， 丁兆民， 曾四鸣， 李铁成， 赵书强， 郝紫惠

(1.国网河北省电力有限公司电力科学研究院，河北 石家庄 050021； 2.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003； 3.国网邢台供电公司，河北 邢台 054001)

0 引 言

风能作为一种可再生清洁能源而得到广泛应用，其大规模接入会对电网的安全稳定运行产生一定影响，可能会增加系统中出现低频振荡特别是区间振荡的风险[1-2]。广域测量系统和同步相量测量单元的应用，有利于实现电力系统广域阻尼控制。但随着广域控制器的普及，控制器间的交互作用与反馈信号的时滞问题逐渐突显，文献[3-4]指出负交互和时滞的作用会恶化甚至破坏系统的安全稳定性。因此，考虑交互与时滞作用的广域阻尼控制成为许多学者聚焦的热点问题。

对于多变量耦合系统的交互作用，处理方式主要有两类，一是对耦合系统进行解耦处理，文献[5]利用等效解耦过程对系统解耦，基于小增益理论提出鲁棒稳定性指标，实现PSS与直流附加控制器的协调；文献[6]实现了供热机组热负荷和电负荷的解耦控制；文献[7]提出基于耦合因子的非线性解耦方法将高阶非线性系统近似转化为一系列解耦的一阶二次和二阶二次子系统。解耦控制原理简单，易实现，但应用于广域控制时会增加控制回路数，可能引发更复杂的多时滞问题。二是降低控制回路间的交互作用，文献[8]在控制环的选择上兼顾控制环对弱阻尼或负阻尼模式的可控可观性和控制环间的交互作用；文献[9-10]根据相对增益矩阵(relative gain array，RGA)得到的控制器间交互作用的量化结果选取交互作用较小的反馈信号，避免复杂的解耦控制；文献[11]基于NI指数理论找到控制器间交互作用最小的变量配对组合，制定多FACTS元件协调控制策略。除了通过选取适当的反馈信号与控制环降低回路间交互作用外，还可以通过协调优化控制器参数提高系统阻尼特性，文献[12]提出利用动态指标值的模型来协调优化双馈风电机组附加阻尼控制器和发电机PSS参数；文献[13]以同步发电机转速偏差为目标函数，利用自适应速度松弛迭代粒子群算法(adaptive velocity update relaxation particle swarm optimisation，AVURPSO)对系统中的PSS、TCSC以及SVC进行协调控制。文献[8-13]虽尽量避免回路间的交互作用，但其耦合关系依然存在，当系统耦合程度较高时，实际效果可能会受到限制。

自抗扰控制[14](Active Disturbance Rejection Control，ADRC)可对不确定因素进行估计与补偿，摆脱控制器对被控对象精确模型的依赖。文献[15-17]分别采用ADRC控制，设计了抑制火电机组低频振荡的本地控制器以及光伏电站和双馈风电场STATCOM的附加阻尼控制器。本文采用ADRC对风电并网系统控制回路间的交互作用进行估计与补偿，实现多变量系统的解耦控制。针对时滞对ADRC控制性能的影响[18]，采用渐消记忆递推最小二乘法实时估计时滞，Smith预估器降低时滞对闭环控制的影响。并以PSO对其参数进行优化。最后采用含风电的新英格兰10机39节点系统，验证控制方法的有效性与鲁棒性。

1 自抗扰控制原理

自抗扰控制是对PID控制的继承与改进，保留了“以误差反馈消除误差”的思想，其结构如图1。扩张状态观测器(Extended State Observer，ESO)对系统状态变量进行跟踪估计，将不确定因素扩张成新状态变量再加以估计，降低控制器对系统精确模型的依赖程度。跟踪微分器(Tracking Differentiator，TD)根据控制目标安排快速无超调的过渡过程，避免PID控制“快速性”和“超调量”之间的矛盾。非线性误差反馈(Nonlinear State Error Feedback，NLSEF)突破了PID控制“加权和策略”在控制性能方面的瓶颈，有利于改善控制器的效率。扰动估计补偿可完成对不确定系统的动态线性化，转换为标准的积分器串联型系统。

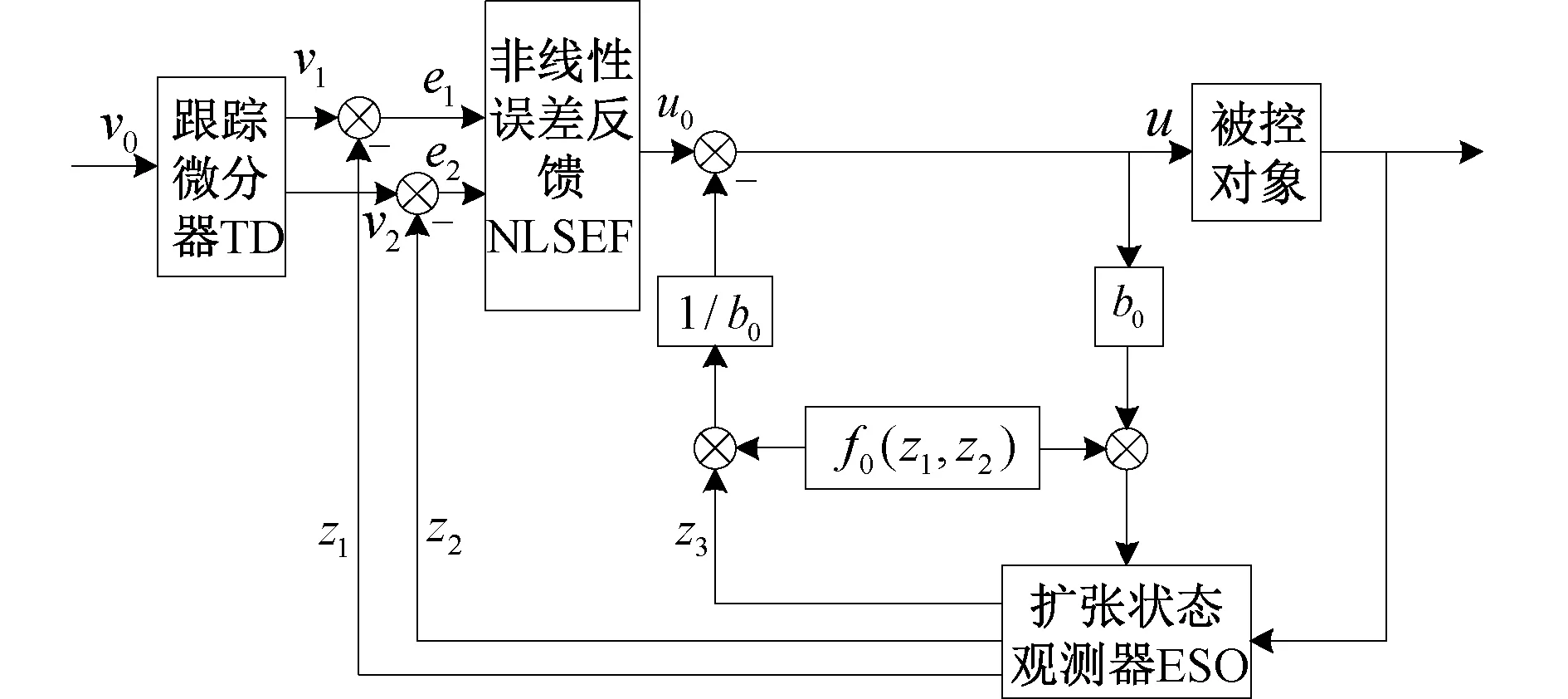
图1 自抗扰控制器的组成Fig.1 Composition of ADRC controller

完整的二阶ADRC算法如下：

(1) 扩张状态观测器 ESO，根据系统输入y和输出u实现对状态变量z1、z2以及z3的估计。

(1)

式中：β01，β02和β03为增益系数；α1，α2为幂函数指数；δ为线性段区间长度；fal为原点附近连续的幂次函数，防止数值仿真时出现高频振颤。

(2) 跟踪微分器TD，根据设定值v0安排过渡过程v1，得到其微分信号v2。

(2)

式中：r0为速度因子；h0为滤波因子；h为计算步长；fhan为最速控制综合函数，算法如式(3)。

(3)

式中:d，d0为fhan函数线性段长度；y，a，a0为fhan的内部参数；sign(x)为符号函数。

(3) 非线性误差反馈NLSEF，利用误差信息e1和e2得到被控对象的误差反馈控制量u0。

(4)

式中:k(e1,e2,P)为关于e1，e2和参数集P的函数，根据需要可为多种反馈函数。为避免高频颤振，采用最速反馈综合函数u0=-fhan(e1,ce2,r,h1)，其中c为阻尼因子，r为控制量的增益系数，h1为快速因子。

(4) 扰动补偿时，最终控制量u由扰动估计量z3和状态误差反馈控制量u0共同决定。

(5)

式中:b0为补偿因子。

2 自抗扰解耦原理

设有式(6)所示多输入多输出的耦合系统

(6)

(7)

此时系统中第i个控制回路的输入输出关系为

(8)

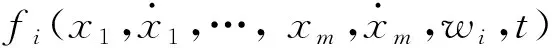
(9)

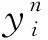
式(9)可以写为

(10)

对其中第i个控制回路构造ESO，对系统状态变量进行估计。

(11)

(12)

式中：u0i为根据式(4)计算出的第i个控制回路上ADRC的输出，因此多输入多输出的耦合系统可近似解耦成式(13)所示的积分器串联型系统。

(13)

3 时滞在线估计

y(ti)=yc(ti-δt)为输出信号yc(ti)时滞后的反馈信号，δt为时滞大小，y(ti)泰勒展开得：

(14)

忽略二次项及更高次项，近似为

(15)

(16)

将式(16)代入式(15)中可得

(17)

式中

(18)

(19)

式(17)是关于θ1和θ2的线性函数，只用两组数据即可求解，并通过θ1和θ2计算时滞为

δt=θ2Δt

(20)

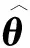
(21)

式中：ρ为遗忘因子，决定算法遗忘程度，值越大，算法遗忘性越小，当ρ=1时，算法退化为一般递推最小二乘法，ρ值过小，会导致估计结果对新数据很敏感，难以在短时间内收敛，因此对其取值应综合考虑辨识精度与收敛速度，一般取 0.95≤ρ<1。

4 自抗扰控制器参数整定

自抗扰控制器参数较多，由于TD、ESO、NLSEF 以及扰动补偿环节功能相互独立，可根据“分离性原理”对各个模块进行整定。TD和ESO的参数主要跟仿真步长h相关[14]，TD中，v0由控制目标决定，r0=10-4/h2，由于根据参数输入值安排过渡过程，所以不需滤除噪声，取h0=h；在ESO中，通常取α1=0.5，α2=0.25，δ=h时，fal(e,α,δ) 的函数性能即能得到保证，β01≈1/h，β02≈1/(2.4×h2)，β03≈1/(15.5×h3)。而NLSEF中c、r、h1和补偿因子b0的选取，与被控对象有关，需反复调试，在多个ADRC控制器的场合下，将大大提高实际操作难度，因此本文采用变惯性因子的PSO对c、r、h1和b0进行协调优化。

多机系统中，针对某一模式进行的阻尼调整会影响甚至恶化其他模式的阻尼[20]，因此综合考虑各振荡模式，目标函数与约束条件为

(22)

(23)

式中：ζi为机电模式的阻尼比；μi为各模式的权重系数；m为机电模式个数；j∈[1,n]，n为控制器个数。基于PSO整定ADRC参数的流程图如图2所示，重复迭代粒子群和惯性因子，直至满足收敛条件，输出优化参数。

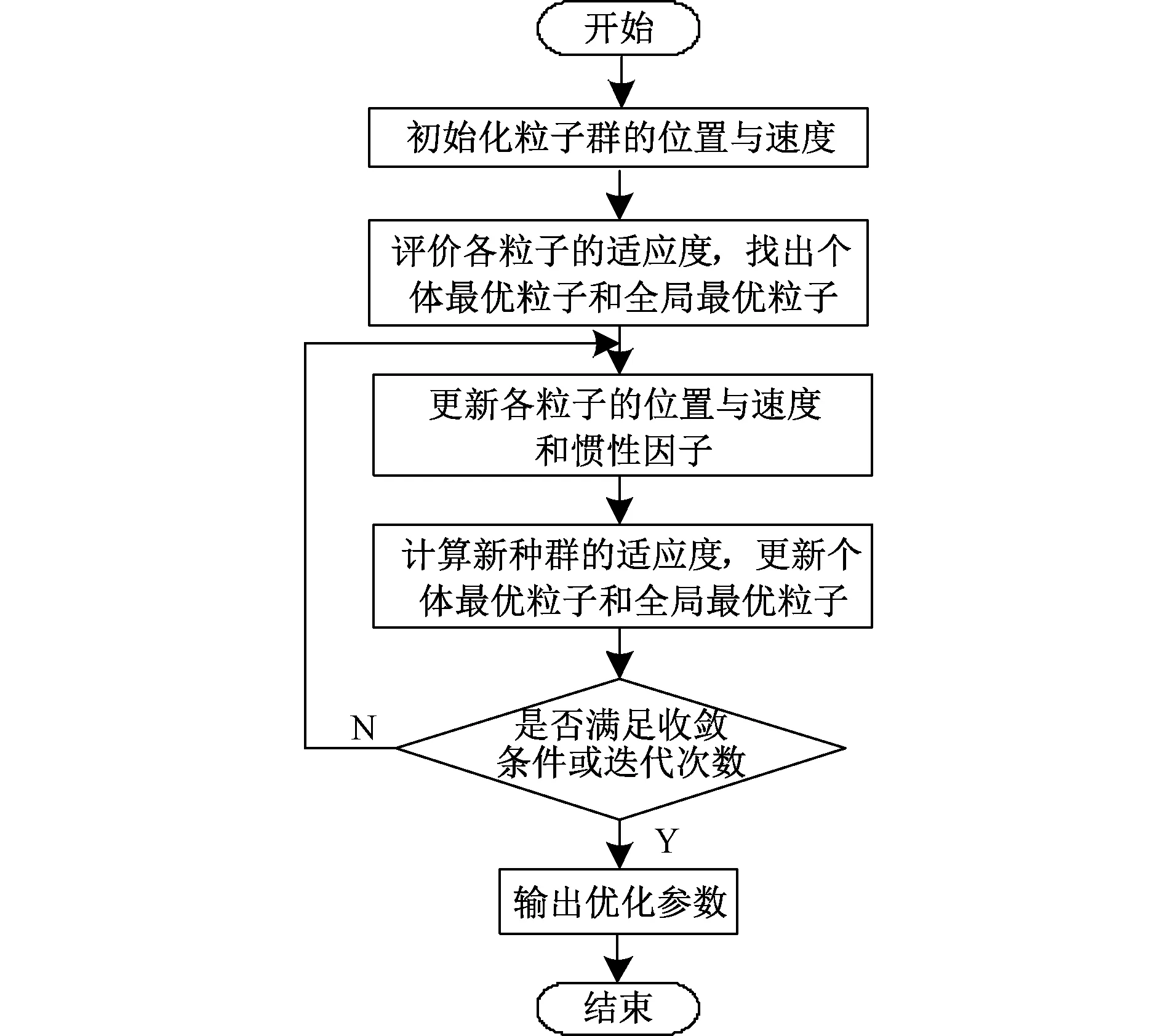
图2 基于PSO的参数优化流程图Fig.2 PSO-based parameter optimization flow chart

5 基于ADRC的广域阻尼协调控制

ADRC应用于多变量高耦合的复杂电力系统的广域阻尼协调控制策略如图3。

图3 广域阻尼协调控制框图Fig.3 Block diagram of wide-area damping coordination control

其中下标i和j分别表示双馈风电场和同步发电机的阻尼控制回路，当出现低频振荡时，切换至阻尼控制模式，以弱阻尼模式可观性较高的转速偏差量Δω作为广域输入信号，渐消记忆递推最小二乘法对信号的不确定时滞进行实时估计，自适应Smith预估器完成对时滞的补偿，经过ADRC控制器和限幅环节后，叠加于相应的控制回路，改善系统阻尼。每个控制回路设置两个带通滤波器，一是滤除低频振荡以外的噪声干扰，提高Smith预估器的抗干扰性；二是平滑处理反馈信号以提高时滞估计的精度。图中G(s)为受控对象的开环传函；Pref和Pg为双馈风电机组有功功率的给定值及测量值；PD为叠加后的有功参考值；Ut和Uref为同步发电机机端电压的测量值和参考值；Us为输入励磁系统的电压偏差；v0是ADRC控制器的预设目标；y是被控对象其他输出信号；τ和τ＇为不确定时滞的实际值和估计值。

基于ADRC的风电并网系统广域阻尼协调控制方法步骤如下：

步骤1：将系统在平衡点附近线性化，根据模态分析结果，选取待改善的弱阻尼振荡模式。

步骤2：针对待改善振荡模式，利用可控可观性指标确定控制器安装位置和广域反馈信号。

步骤3：求解控制回路上被控对象的开环传函数G(s)，并据此设计自适应Smith预估器。

步骤4：按照分离性原则设置与仿真步长相关的参数，利用PSO整定ADRC控制器中与实际被控对象有关的参数。

6 仿真分析

以图4所示含风电场的系统为例[21]。由20台5 MW的双馈机组组成的风电场接入节点16。

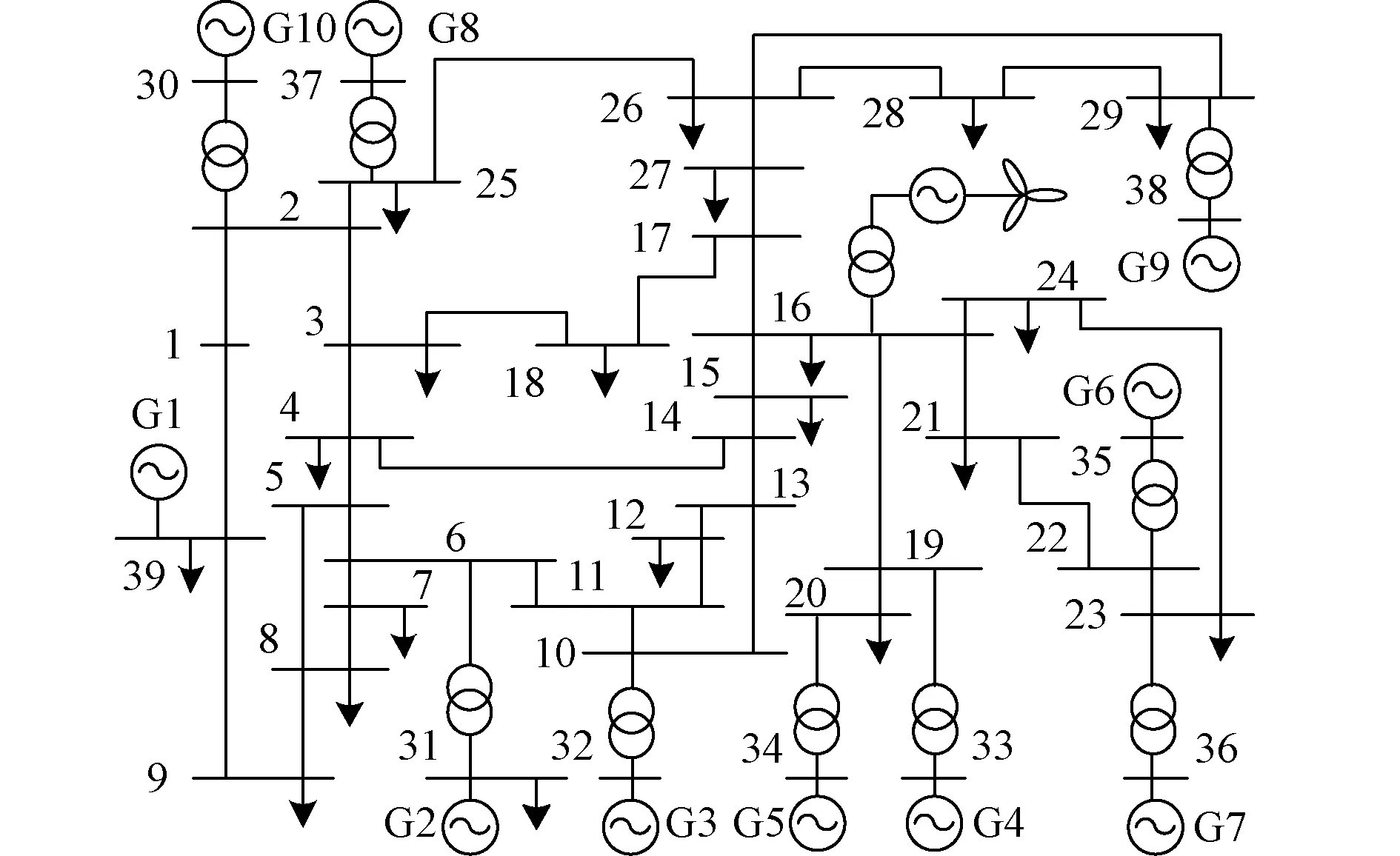
图4 新英格兰10机39节点系统Fig.4 10-machine 39-bus New England system

6.1 控制器选址与选取反馈信号

表1为机电振荡模式分析结果。

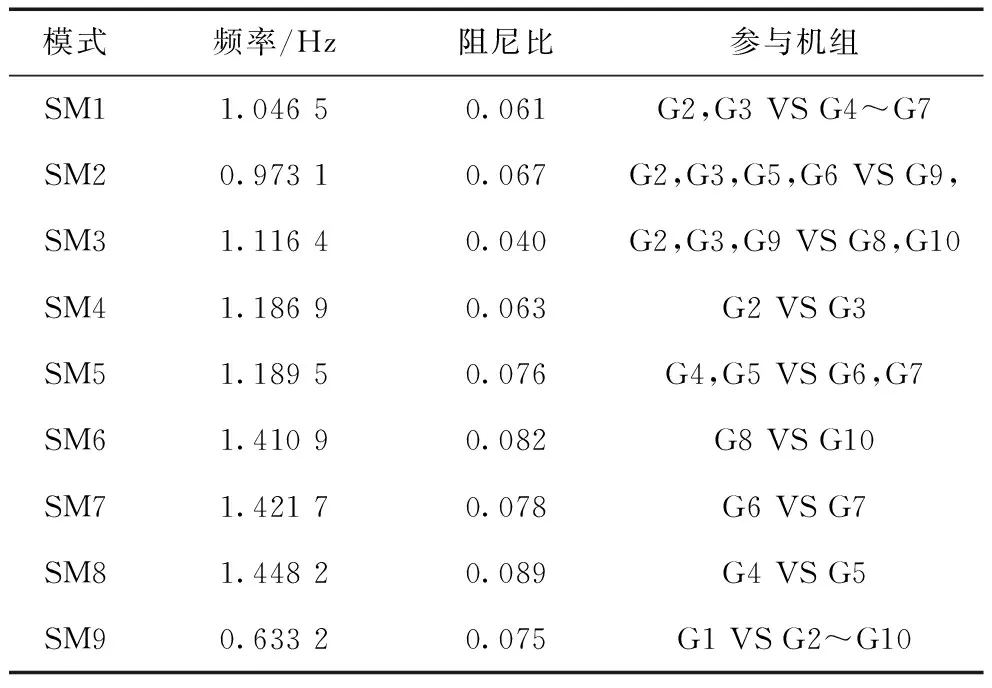
表1 含风电场的测试系统模态分析结果

从表1可知，区间振荡模式为：模式SM1、SM2、SM3和SM9。其中SM9参与机组最多，振荡频率最低，为0.633 2 Hz，该模式中，G1的可控性指标最高，双馈风电场次之，但G1为外部系统等值机，因此考虑双馈风电场的附加阻尼控制抑制SM9，并根据可观性指标选取G5的转速偏差作为输入信号。对模式SM1、SM2和SM3进行控制器选址与反馈信号的选取，控制器依次安装在发电机G2、G9以及G10，反馈信号依次为发电机G3、G2以及G9的转速偏差。

6.2 控制器设计

图4所示系统是复杂的高阶系统，难以通过物理建模求取受控对象传函，因此可通过辨识得到被控对象的开环传函G(s)。以双馈风电场控制回路为例，在DFIG机侧有功功率控制信号上施加0.5 s脉冲扰动，以Δω5作为输出信号，利用Matlab辨识工具箱的N4SID算法辨识受控对象的开环传函GDFIG(s)=N(s)/D(s)，其中

N(s)=-1.145×10-5s11-6.277×10-4s10-

7.64×10-3s9-9.516×10-2s8-

0.840 3s7-4.164s6-27.3s5-42.76s4-

163.6s3-117.1s2-90.04s-2.987

D(s)=s11+7.2s10+123.1s9+688.9s8+

4 878s7+2×104s6+6.9×104s5+1.8×

105s4+2.7×105s3+2×105s2+

8.063×104s+6 023

辨识结果和被控对象响应曲线的对比如图5，可以看出，辨识模型基本反映出系统的主要特征，因此可根据该辨识结果设计ADRC控制器。

图5 脉冲响应曲线Fig.5 Impulse response curve

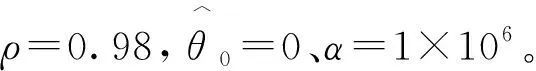
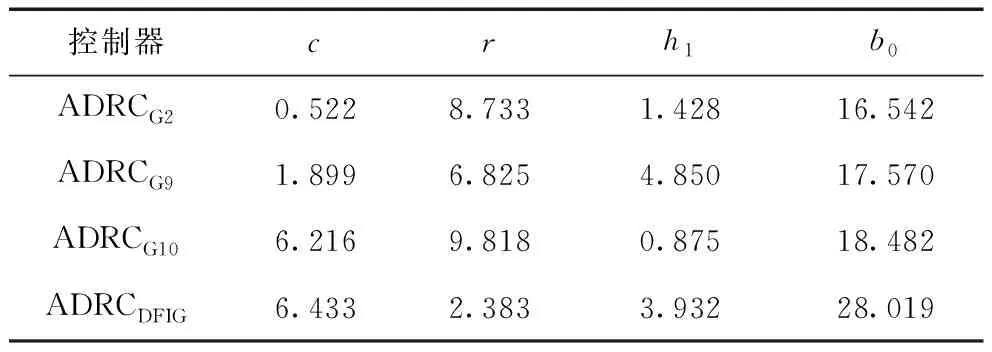
表2 控制器参数优化结果

6.3 时域仿真

线路L04-14在2 s时发生三相短路故障，2.2 s时切除故障。采用威布尔分布的随机风速模型，平均风速为8.862 m/s，仿真时间为20 s。

6.3.1 ADRC与PSS控制效果仿真对比

为验证控制策略的有效性，在控制器位置和反馈信号相同的情况下设置以下四种控制方案：

方案1：同步发电机与双馈风电场均采用PSS，每个PSS参数单独整定，目标函数为式(22)，待优化参数及其上下限见文献[22]。

方案2：同步发电机组与双馈风电场均采用PSS控制器，协调优化全部PSS的参数。

方案3：同步发电机与双馈风电场均采用本文设计的ADRC控制器，控制器参数单独整定。

方案4：同步发电机组与双馈风电场均采用本文设计的ADRC控制器，控制器参数协调优化。

仿真结果如图7，NC表示无附加阻尼控制。从图7可以看出，当无附加阻尼控制时系统振荡时间最久，到15 s时才逐渐平息下来。四种控制方案都能产生阻尼作用，能够使系统在10 s时恢复稳定状态，协调优化方案比单独优化时的控制效果好，阻尼效果更明显，说明协调优化可以更好的发掘系统内多个控制器的整体性能。对比方案2与4的控制效果可知，ADRC控制器估计与补偿不确定因素的特点有利于降低不同控制回路之间的相互影响，从而避免回路间负交互作用对控制器性能的削弱。

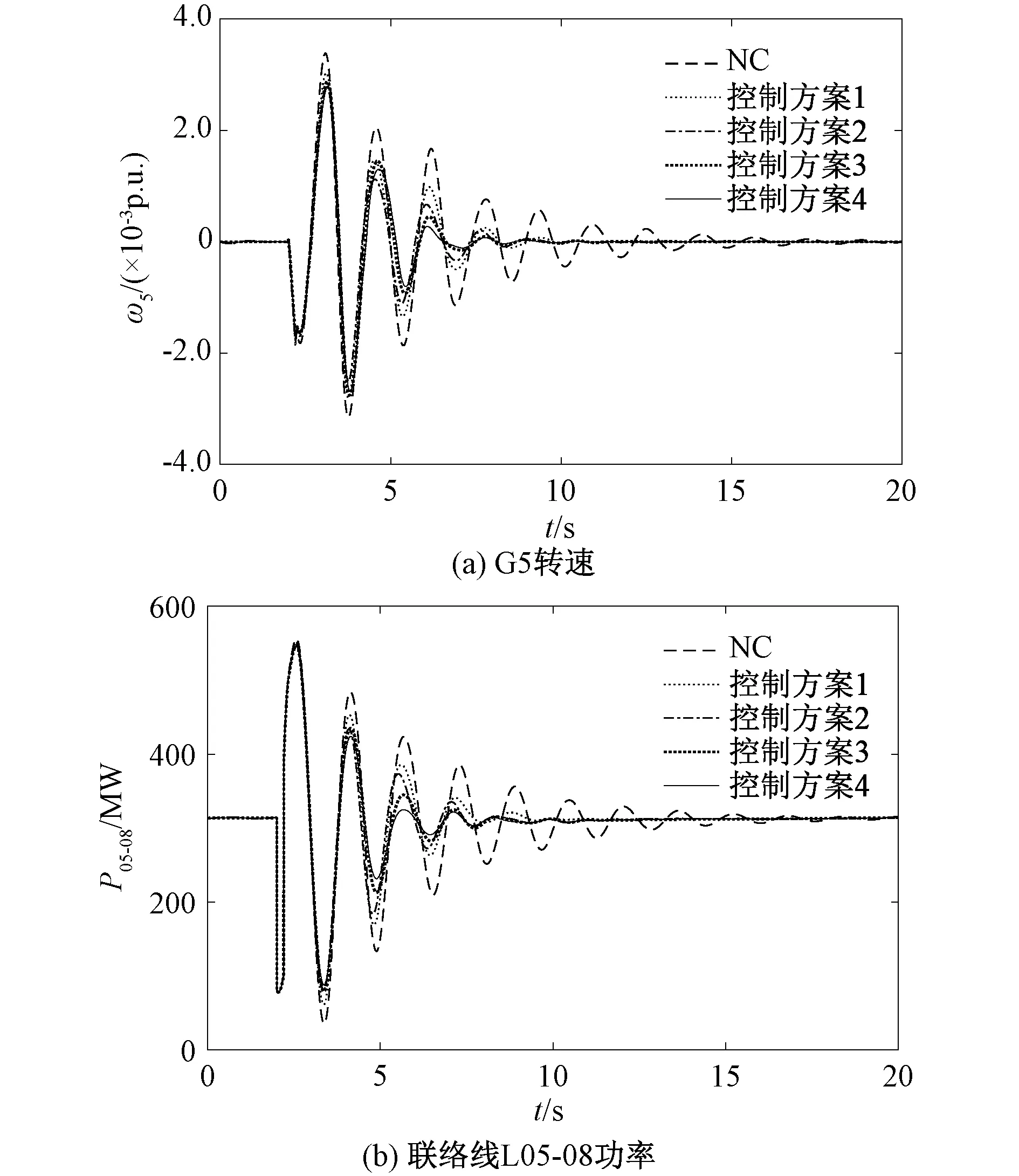
图7 多种控制方案下的仿真曲线 Fig.7 Simulation curves under various control schemes

6.3.2 反馈信号对控制效果的影响

为比较不同反馈信号选取方法对控制效果的影响，设置方案5：根据相对增益法选取反馈信号，同步发电机组与双馈风电场均采用本文设计的ADRC控制器，并协调优化控制器参数。

为分析初选信号与控制回路间的交互作用，计算相对增益增益矩阵Λ：

根据相对增益理论，各控制器选择相对增益接近1的输出作为反馈信号。

从仿真结果(图8)可以看出，方案4使系统振荡衰减更快，体现出更好的控制效果。这是由于相对增益法是以牺牲反馈信号的可观性为代价来降低回路间交互作用，从而影响阻尼效果。

图8 不同反馈信号下的仿真曲线Fig.8 Simulation curves under different feedback signals

6.3.3 时滞对控制效果的影响

广域信号的使用会引入时滞问题，为验证本文控制策略在时滞条件下的鲁棒性，设置两种固定时滞：150 ms和250 ms。

渐消记忆递推最小二乘法对时滞状况的估计结果如图9，从图9可以看出，估计结果快速接近实际值，随着时滞的增加，估计结果与实际值会出现一定误差，是由于忽略了时滞信号泰勒展开式的高阶项，当时滞较小时，忽略部分的影响很小，当时滞较大时，结果的误差会有所增加。

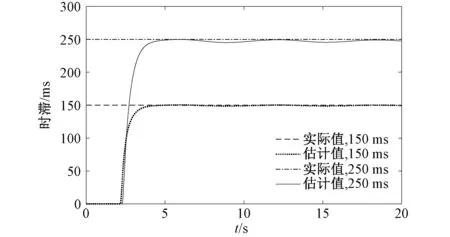
图9 两种时滞条件下的估计结果 Fig.9 Estimation results under two time-delay conditions

图10为方案2和4在两种时滞下的仿真结果，从图10可以看出，在两种时滞下方案2将失去阻尼系统振荡的能力，系统失去稳定，而方案4仍然使系统迅速恢复稳定状态，且仿真曲线非常接近。虽然时滞估计环节具有一定误差，但是ADRC良好的抗干扰性，能够承受一定范围的时滞，说明本文控制策略对时滞具有较高的鲁棒性。

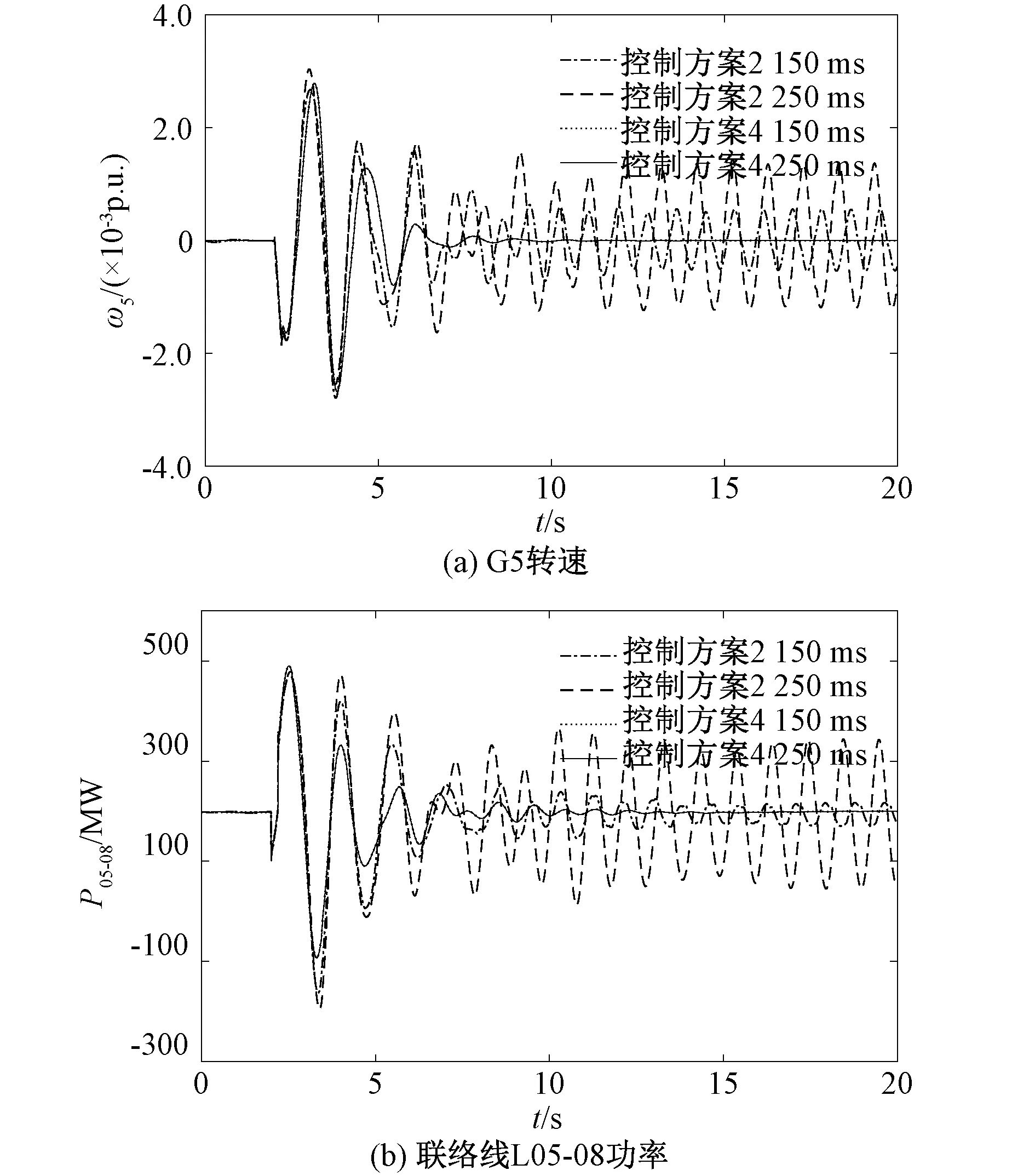
图10 两种时滞条件下的仿真曲线Fig.10 Simulation curves under two time-dela conditions

6.3.4 控制方案对不同工况的适应性

为验证控制方案在不同工况下的适应性和鲁棒性，在节点36接入一个由60台5 MW的双馈机组组成的风电场，设置200 ms的固定时滞，其余步骤均与上文相同。仿真结果如图11，从图中可以看出，采用控制方案2时系统失去稳定，而控制方案4依然具有较好的阻尼效果，验证了本文所提控制方案的有效性和鲁棒性。

图11 其他工况下仿真结果Fig.11 Simulation curves under other operation conditions

7 结 论

本文提出一种基于ADRC的广域阻尼协调控制策略，利用ADRC估计并补偿回路间的交互作用，以渐消记忆递推最小二乘法实现时滞估计，采用PSO协调优化控制器参数。以含风电的新英格兰10机系统为例进行验证，主要结论如下：

(1)相较于传统PSS，ADRC控制器在抑制低频振荡时，具有收敛数度快、超调量小、时滞鲁棒性强的优点。

(2)相较于单独优化每个控制器，协调优化更有利于提高系统整体阻尼特性。

(3)相较于相对增益法选取反馈信号，本文方法可充分反馈信号的可观性，提高控制器的阻尼作用。