基于深度学习的SIMON32/64安全性分析
王慧娇 丛 鹏 蒋 华 韦永壮
(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)
近年来,伴随无线传感器网络以及射频识别技术的发展和广泛应用,对资源受限的设备进行数据加密需要使用轻量级的密码算法.然而轻量级的密码算法追求低消耗与高效率,必然会导致安全性的降低,针对这一问题目前还没有公认的设计准则与安全标准,因此有必要对这些轻量级算法的安全性进行分析.
一个轻量级分组密码的分析关键在于构造一个有效的区分器,即根据密码算法的结构或其组件的特征将原密码算法和随机置换进行区分.差分区分器是迄今已知的攻击分组密码最有利的工具之一,由Biham等人[1]首次提出,该工具利用了分组密码算法在迭代过程中存在不平衡的差分统计量分布.轻量级分组密码在设计之初会充分考虑抵御差分密码分析和线性密码分析.如何发现未知的算法缺陷,设计新型区分器是一个新的研究方向.人工智能的飞速发展与深度学习技术的进步息息相关,在计算机视觉[2]、自然语言处理[3]、生物信息[4]等领域深度学习具有广泛的应用.深度学习是一种从数据当中发现复杂规律,并且利用规律对未来时刻、未知状况进行预测和判定的方法,因此深度学习在解决密码学问题上具有潜在的优势.
就密码学而言,深度学习主要应用于侧信道分析[5],对深度学习技术在经典密码分析的适用性上没有进行过多探讨.Abadi等人[6]认为神经网络通常意味着并不擅长密码学,简单的感知机甚至无法对异或运算进行区分,而这恰恰是许多密码算法的基础.Rivest[7]则评价了深度学习与密码学之间的多种联系,提出了使用深度学习应用于密码分析中的一些可能的研究方向.Hu等人[8]开发了一种前馈神经网络(feedforward neural network, FNN),该网络可以从AES密码的密文中发现明文,而无需使用密钥信息.Gohr[9]在2019年美密会上提出了基于深度学习的减轮SPECK32/64改进差分攻击,通过训练卷积残差神经网络用以区分固定明文差分加密的密文对和随机数据并以此构造区分器,证明了深度学习在对称密码上攻击的有效性和研究方向.Baksi等人[10]延续Gohr的工作并借鉴文献[11]的思想利用神经网络构造多合一差分区分器应用于非马尔可夫密码GIMLI. Yadav等人[12]将差分区分器和深度学习技术结合,对经典差分区分器设计了基于深度学习的通用扩展,使区分器具有更多的轮数且需要更少的数据复杂度.Bellini等人[13]采用多层感知机和卷积神经网络(convolutional neural network, CNN)来构造减轮TEA和RAIDEN算法的神经网络区分器,并提出了传统区分器无法应用的场合以及该方法的局限性.Jain等人[14]对轻量级密码算法PRESENT构造3~6的神经网络区分器,该区分器能够将密码数据和随机数据以极高的概率区分开,进一步拓展了深度学习在分组密码的工作.So[15]尝试利用深度学习对简化版本的DES,SPECK和SIMON在基于密钥空间受限下的全轮攻击,成功发现了明/密文对和密钥之间的线性近似,但在密钥空间不受限制的条件下,该方法并不适用.
2013年轻量级分组密码SIMON[16]一经发布,便受到了广泛的关注.最初由Abed等人[17]采用传统差分分析获得了SIMON算法在各种分组长度下的高概率差分特征.Biryukov等人[18]在FSE’14对自动化搜索算法寻找差分路径进行改进,提出了基于ARX(addition rotation exclusive-or)密码的阈值搜索技术.该方法能够更有效地利用密码算法的强差分效应,进一步改善了SIMON类算法的最佳差分.Kölbl等人[19]在2015年美密会上提出关于SIMON系列密码的差分和线性分布特征,采用自动化搜索技术SAT/STM寻找最佳的差分和线性特征,并研究了在不同轮数下SIMON算法抵抗攻击的能力.但是这类方法在构造区分器的过程中数据复杂度和时间复杂度相对较高.如何针对SIMON算法构建更加智能化、便捷化的深度学习区分器有待进一步去解决.
本文借鉴差分密码分析的攻击思想,通过深度学习发现轻量级分组密码在迭代过程中存在的差分不均匀性,提出了基于深度学习的减轮SIMON32/64的区分器模型,该区分器可以将密码算法和随机数据以极高的概率区分开.这是对SIMON算法安全性分析的全新思路,相较于传统的区分器具有更强的通用性和可实现性.该方案采用FNN和CNN深度学习算法来构造区分器,讨论了在相同环境下2种模型各自具有的优势.进一步通过对FNN和CNN区分器进行结合构造混合区分器,在保持模型的相对精度下,增加个体间的差异,提高区分器的泛化能力.通过实验结果证明,混合区分器在进行侯选密钥的筛选任务时能够以相对较高的概率将真实子密钥的范围确定在一个三者最小的集合中.与文献[18-19]相比,本文提出的深度学习区分器具有较好的性能,详细的9轮攻击复杂度对比如表1所示:
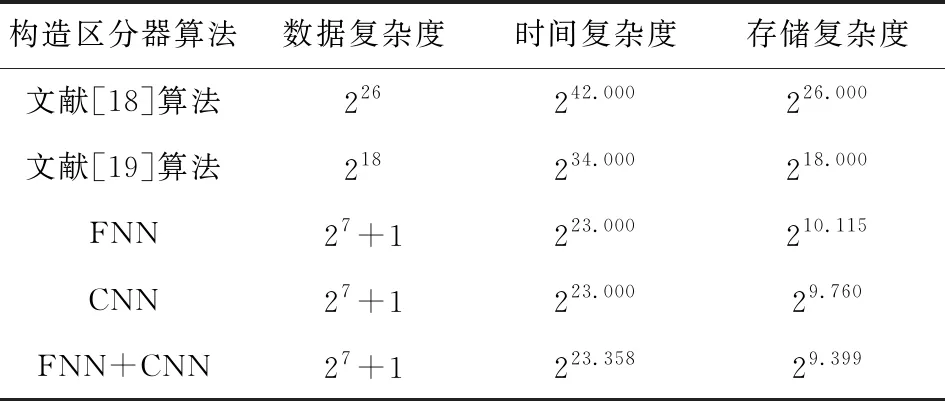
Table 1 Comparison of 9 Rounds of Attack Complexity for SIMON32/64
1 预备知识
1.1 SIMON算法
轻量级分组密码SIMON[16]基于平衡Feistel结构,其设计上只使用了简单的与运算、异或运算、移位运算,特别适用于物联网设备当中.其可选择的分组长度为2n,其中,n取值为16,24,32,48,64,主密钥长度为n×m,其中,m取值为2,3,4,设计者基于不同n和m以及迭代轮数给出了SIMON算法的多个版本.其非线性变换为
F(x)=(x<<1) & (x<<8)⊕(x<<2).
(1)
假设其输入为(Li,Ri),子密钥为ki,经过1轮加密后其输出为
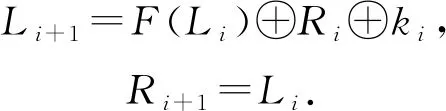
(2)
图1为SIMON的1轮迭代变换结构,其中<<为左移运算符、&为与运算符、⊕为异或运算符.
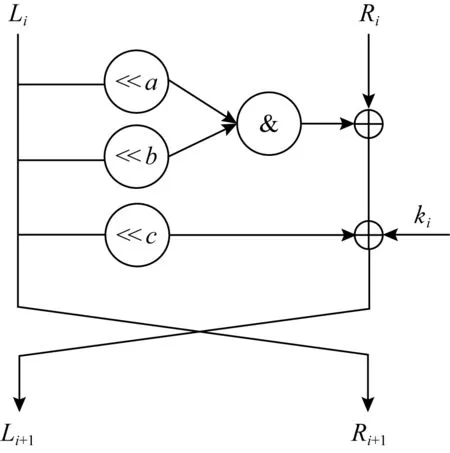
Fig. 1 Process of SIMON single round encryption图1 SIMON单轮加密过程
1.2 前馈神经网络与卷积神经网络
FNN和CNN在设计上具有相似性同时也存在差异,因此对数据集进行处理的过程中会有不同的敏感偏好.
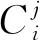
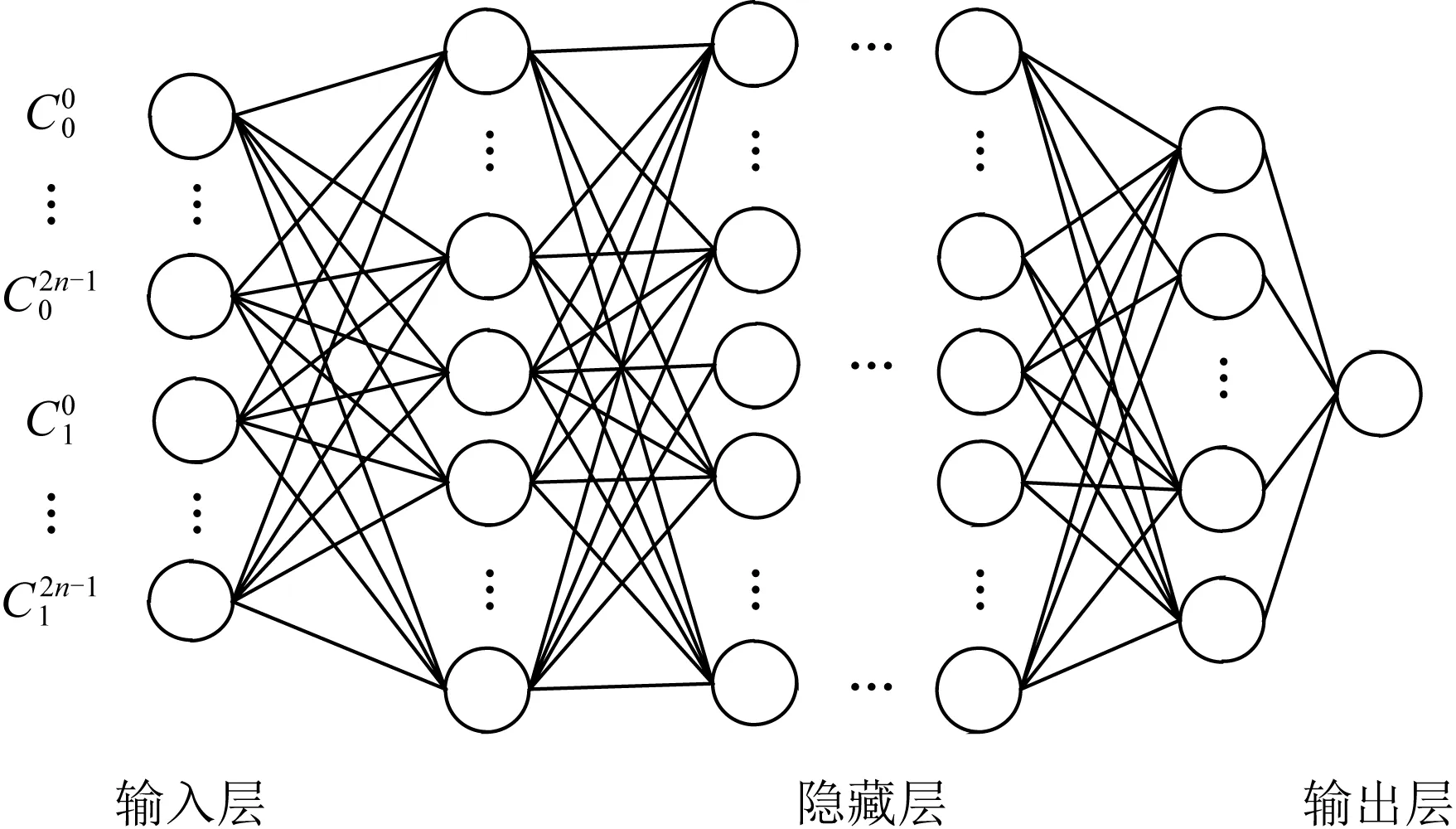
Fig. 2 Model of feedforward neural network distinguisher图2 前馈神经网络区分器模型
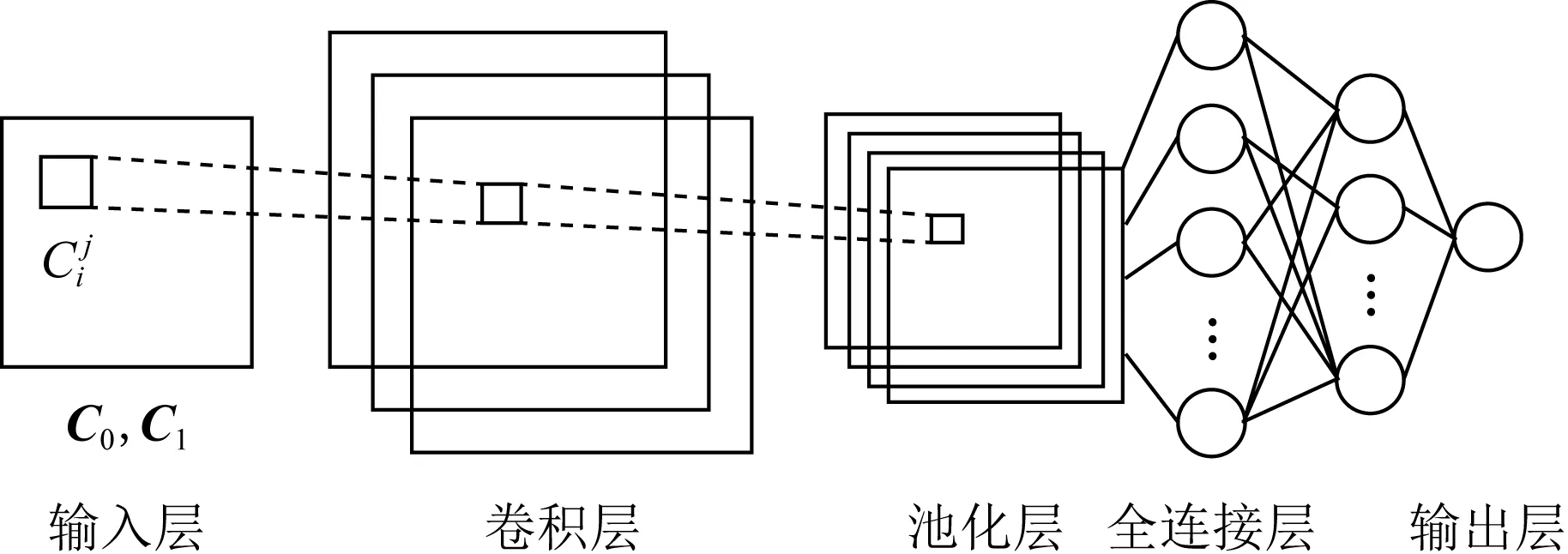
Fig. 3 Model of convolutional neural network distinguisher图3 卷积神经网络区分器模型
CNN是一种特殊结构的FNN,能够接受矩阵作为输入,具有跨空间(图像等)或跨时间(音频信号等)的重复神经元块(卷积核),这种特殊的设计结构使得CNN具有部分平移不变性.图3给出了CNN区分器的模型,其中输入层可由密文对(C0,C1)灵活设置其矩阵的尺寸.
以截断差分区分器为例:算法只考虑差分的一部分性质,比如,差分落在某个集合中以及差分的某个比特位为0.对于不同的数据集这些差分集合以及其中的某比特可以落在空间中的任意位置,假如要像FNN一样在每个空间位置学习独立的权重,训练数据需要多出几个数量级.简单地说,对于没有跨空间重复权重的FNN,连接到输入矩阵左上方的输入神经元组不得不独立于连接到输入矩阵右下方的输入神经元组来学习表示某个差分集合或某个比特位.因此需要足够多的训练样本,才能够让FNN学习到某些差分集合在各个可能位置.
2 基于深度学习的区分器设计
本节采用1.2节中的2种深度学习模型来构建深度学习区分器,给出了深度学习区分器的构建方法和实现过程,以及如何利用该区分器进行候选密钥筛选.
2.1 区分器的设计
轻量级分组密码在迭代轮数低的情况下,明文中的统计规律和结构特征没有完全隐藏在密文当中,本文期望通过深度学习发现这种隐含的特征,从而将密文对和随机数据区分开,进而筛选出具有高概率差分特点并且隐含了密钥信息的密文对.对此本文选取了2种网络结构模型:FNN和CNN,通过灵活调节超参数,使其达到最优的性能.一方面是为了验证2种神经网络结构对于加密数据的敏感度;另一方面通过结合2种神经网络区分器进行候选密钥筛选,得到更好的结果.
深度学习技术能够揭示数据中的隐藏结构而无需显式标注其特征,借鉴差分密码分析中寻找多条差分特征的思想将其转化为深度学习的分类问题,采用2阶段策略构造深度学习区分器:
1) 离线阶段
离线阶段是对神经网络进行2分类学习,训练集与验证集由密文对和随机数据组成.密文对来自于固定明文差分通过不同密钥加密r轮生成.
2) 在线阶段
在线阶段是通过神经网络进行预测.测试集来自于固定明文差分采用统一密钥进行加密r轮生成的密文对.确定区分器阈值δ,当测试样本预测值大于δ时将其归类为正例,否则归类为负例.
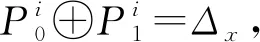
算法1.离线阶段.
输入:样本数量n、明文差分Δx;
输出:训练成功的网络模型model.
①TD←∅; /*初始训练集为空*/
②P0,K←Random;P1←P0⊕Δx;
③C0←encrypt(P0,k);C1←encrypt(P1,k);
④ fori∈{1,n} do /*设置样本集标签*/
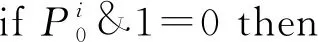
⑥Ci←Random;
⑦Yi←0;
⑧ else
⑨Yi←1;
⑩ end if
算法2.在线阶段.
输入:样本数量n、明文差分Δx、阈值δ、模型model;
输出:隐藏密钥信息且具有高概率差分密文对.
①TD′←∅; /*初始测试集为空*/
②P0←Random;P1←P0⊕Δx;
③C0←encrypt(P0,k); /*唯一密钥加密*/
④C1←encrypt(P1,k);
⑤TD′←X(C0,C1);
⑥ fori∈{1,n} do

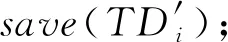
⑨ else
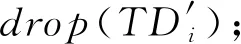
2.2 神经网络的设置
为了保留密文对的统计信息以及神经网络模型能够顺利收敛到一个局部最优解,分别对输入输出格式、激活函数、部分超参数进行设置.
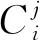
2) 基于不同的数据集和应用场景神经网络在训练过程中采取不同的非线性激活函数:sigmoid函数是1个logistic函数,表示为不管输入是什么得到的输出被约束在0~1之间.本文中的神经网络模型只有1个输出神经元,因此将其应用于输出层,其函数表达式为
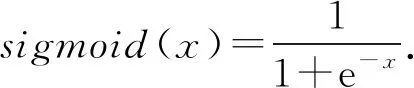
(3)
ReLU函数应用于轮数比较低的区分器训练当中,减少了梯度消失的可能性,其函数表达式为
ReLU(x)=max(0,x).
(4)
当对轮数比较高的区分器进行训练时,由于数据集当中的密文对和随机数据没有出现明显的差异性,因此往往在训练过程中产生梯度爆炸的情况,训练模型存在向2个方向倾斜的可能,基于此本文选择了tanh函数,其函数表达式为
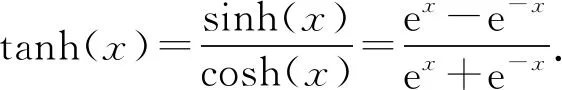
(5)
3) 超参数设置.损失函数设置为其均方误差
(6)
同时为了防止出现过拟合现象,对均方误差采用L2范数最小化结构风险.每批次(batch)训练数据为213,优化器采用Adam算法,学习率随训练轮数不断下降,经过20个回合(epoch)后不再降低,所以,算法中训练周期设置为20个epoch.其间通过回调函数触发ModelCheckPoint方法保存最佳的学习模型.
2.3 候选密钥筛选方案
采用上述算法获得了一个r-1轮深度学习区分器,对一个r轮加密算法,其攻击步骤为:
1) 均匀随机的选取明文P0,令P1=P0⊕Δx,在同一密钥k(k∈k1,k2…,kr)下加密,获得相应密文对(C0,C1).
2) 对(C0,C1)利用其r轮中所有存在的候选密钥进行1轮“解密”,得到其r-1轮密文对(σ0,σ1).
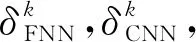
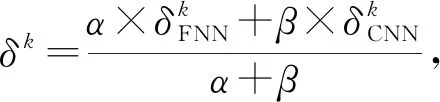
(7)
其中,α,β由FNN和CNN区分器的准确率分配.
4) 进一步统计每一个候选密钥来自于解密后的得分
vk
(8)
通过vk对所有候选密钥进行排名.算法3对步骤1)~4)进行了阐述.
算法3.候选密钥筛选.
输入:选择明文差分加密r轮的密文对(C0,C1)、r-1轮深度学习区分器modelFNN,modelCNN;
输出:候选密钥排名.
① fori∈{1,n} do /*n为候选子密钥数量*/
②σ0←decryptOneRound(C0,ki);
③σ1←decryptOneRound(C1,ki);
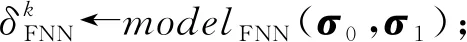
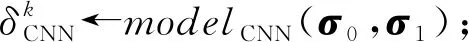
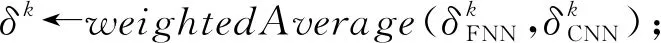
⑦vk←finalGrade(δk);
⑧ end for
⑨descendingSort(vk). /*降序排列*/
3 实验结果与分析
本节主要给出了深度学习区分器在训练阶段和测试阶段的实验结果,并展示了通过深度学习区分器在对SIMON32/64的9轮攻击中呈现的效果.所有实验平台其硬件环境为处理器:Intel®CoreTMi7-7700,内存:8.00 GB.深度学习库:后端Tensorflow,前端Keras,采用CPU进行计算实现.
3.1 离线阶段实验
选择明文差分Δx=0x0040/0000,通过第2节的算法1生成220个训练集样本,217个验证集样本,正负样本的数量各占其中的1/2.图4给出了基于6轮FNN在20个回合的训练情况:
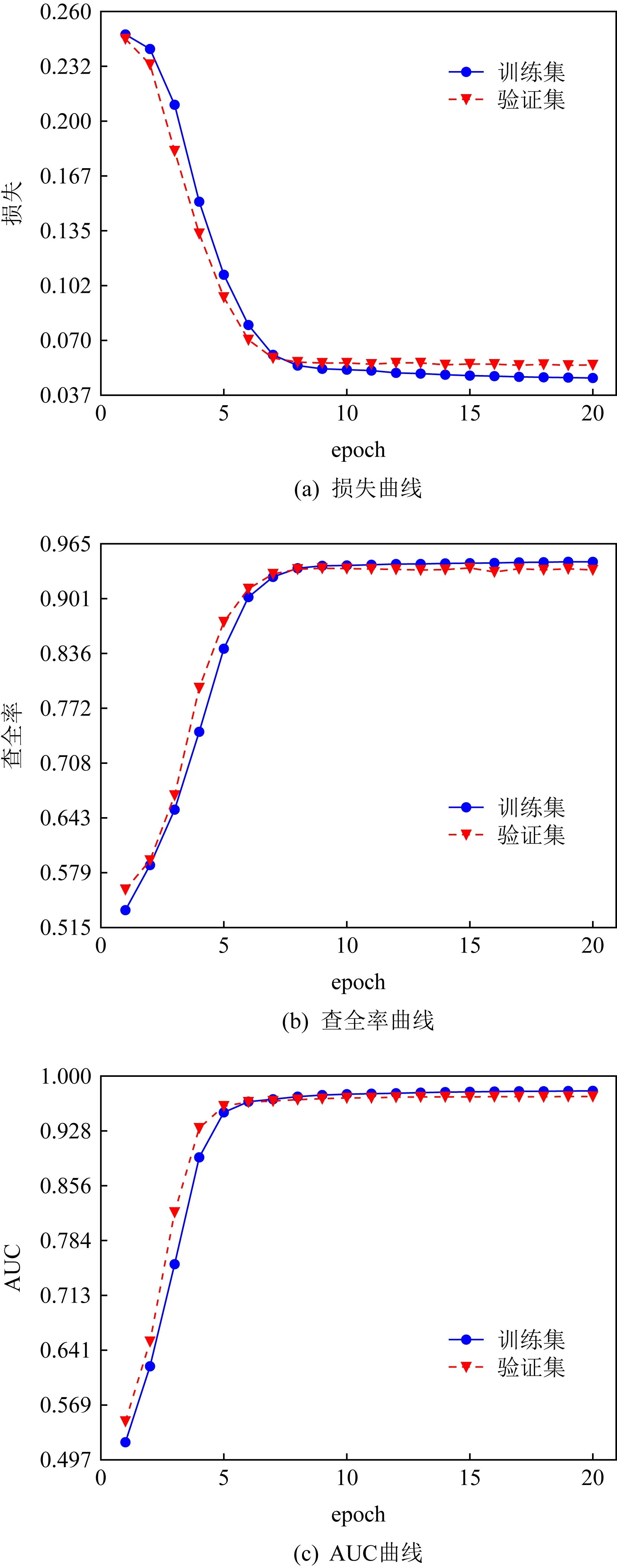
Fig. 4 Performance measurement of SIMON 6-round neural network differentiator图4 SIMON的6轮神经网络区分器的性能度量
损失曲线能够反映模型的学习率变化和函数的收敛情况,在图4(a)中,由于初始时学习率设置较大,损失值下降很快.随着迭代学习率不断得到调整,模型的训练精度增加,损失曲线也逐渐趋于稳定.其后面epoch验证集的曲线变化有向低性能过渡的趋势,反映出模型存在轻微的过拟合现象.查全率表示被预测正确的正例样本占总正例样本的比例,衡量了区分器对正例的识别能力.其20个epoch的查全率变化如图4(b)所示,反映该模型能够比较全面地选择出更多的密文对,从而能够寻找出更多的高概率差分.AUC(area under curve)反映了模型对样本的排序能力,它能够直观地展示一个模型的好坏.图4(c)展示了在第6个epoch后AUC的值开始接近于1,说明采用Δx=0x0040/0000为初始差分经过6轮迭代后生成的密文对与随机数据之间存在较大的差别,神经网络能够轻易地提取到这种数据间差异.综上说明这是一个近乎完美的6轮区分器.
表2列出了FNN和CNN在6~9轮区分器的学习参数、训练时间和准确率.可以看出CNN能够更好的收敛到一个局部最小值,更容易被优化.但相应的由于FNN结构简单,训练时间将大大降低,准确率上略逊于CNN.
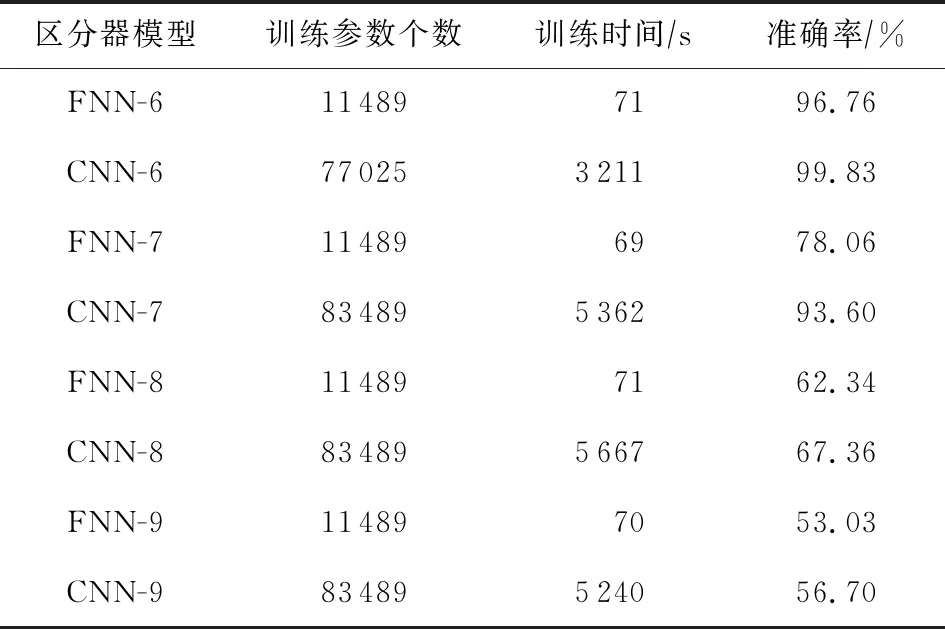
Table 2 Comparison of SIMON32/64 6~9 Rounds FNN and CNN
图5展示了6~9轮区分器训练过程中验证集准确率的变化,表明深度学习区分器对低轮的SIMON算法轻松的学习到了加密数据和随机数据的区分,但随着其迭代轮数的增加,准确率会不断降低.其本质原因在于根据密码算法的混淆和扩散原则,其迭代轮数越高,明密文之间的统计信息越弱,相应的正负样本相似性很高,使深度学习难以进行有效的特征选择.为了使8,9轮的区分器有更强的泛化能力,通过增加训练集和验证集的数据量、延长训练epoch,2种神经网络模型都获得了不同程度的提升,CNN相比于FNN提升效果更加明显.
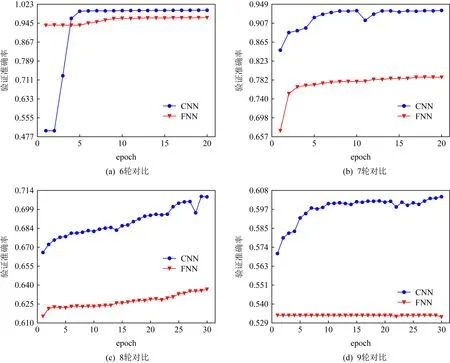
Fig. 5 Comparison of the accuracy in verification set of SIMON 6~9 rounds FNN and CNN图5 SIMON的6~9轮FNN与CNN验证集准确率对比
3.2 在线阶段实验
对2种神经网络模型6~9轮进行测试,采用选择明文差分为Δx=0x0040/0000,定义阈值δ>0.5.为了防止可能存在的密钥依赖,每一轮采用1 000个密文对作为数据集,循环1 000次,总计100万个数据集.表3给出了2种神经网络模型6~9轮的预测结果,可以看出2种模型在6,7轮都具有可信的准确率,同时证明该模型具有良好的泛化能力.在8,9轮中,CNN在预测上具有一定的参考意义,基于9轮的FNN几乎没有学到任何东西.图6给出了6轮CNN区分器对300个随机正样本的预测分布.可以看出我们的6轮CNN区分器在预测值的分布上具有较高的可信度,能够容易地找到具有高概率差分的密文对.
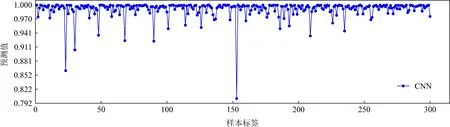
Fig. 6 Prediction results of SIMON 6 rounds of convolutional neural network图6 SIMON的6轮卷积神经网络预测结果
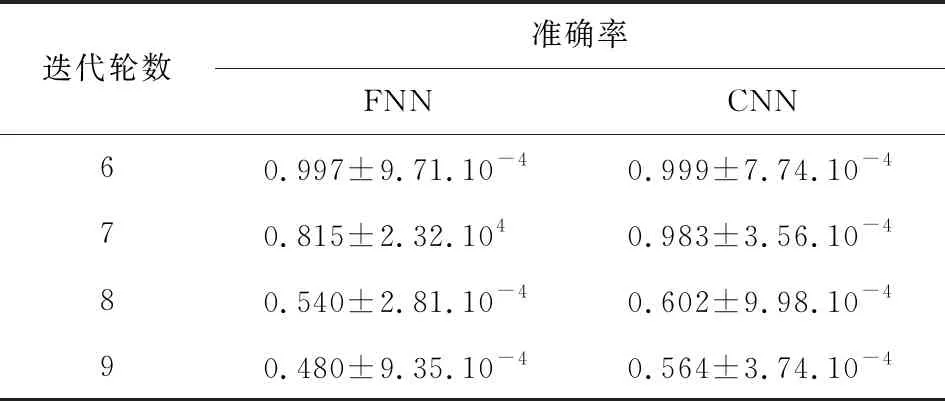
Table 3 Test Set Accuracy of Deep Learning Distinguisher表3 深度学习区分器测试集准度
3.3 候选密钥筛选结果
训练集包含220个样本,验证集包含217个样本,每批次采用213样本,训练epoch为20轮.模型初始学习率为0.02,每轮递减5E-4,经过20个epoch后学习率为0.01.最终得到了基于FNN和CNN的最佳学习模型.故其每个区分器的离线复杂度为220+217=220.170(加密次数).
利用算法1构造了一个7轮的深度学习区分器.采用128个输入差分为Δx=0x0040/0000的已知明文对,基于SIMON32/64的自身性质,对其无损失的向上扩展1轮,最后通过真实密钥加密至9轮.
利用算法3对9轮SIMON32/64的65,535个候选密钥进行筛选.采用27个选择明密文对,该攻击的时间复杂度为220.170+27×216=223.000(加密次数),混合区分器的攻击时间复杂度为220.170×2+27×216=223.358(加密次数).
通过对FNN和CNN以及两者结合的混合区分器进行实验,表4给出了以真实密钥为分界线,高于真实密钥成绩的候选密钥数量.筛选出的候选密钥数量越少,表明所设计的区分器越有效.候选密钥成绩的平均取值范围在-537.107~-500.221之间.
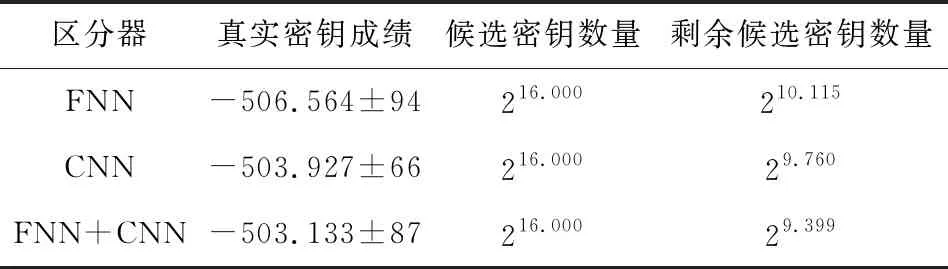
Table 4 The Number of Candidate Keys and the Actual Key Scores
3.4 深度学习区分器与传统区分器的比较
采用STA/STM方法Kölbl等人[19]给出了减轮SIMON32/64的16轮差分轨迹,其中6~9轮的差分轨迹的转移概率分别为2-12,2-14,2-18,2-20,相应所需的数据复杂度和存储复杂度至少分别需要212,214,218,220.采用深度学习构造的区分器在9轮攻击中数据复杂度仅为27+1,FNN和CNN以及两者结合的混合区分器存储复杂度分别为210.115,29.760和29.399.表1对文献[18-19]和深度学习区分器所需的数据复杂度、时间复杂度和存储复杂度进行了总结,可以反映出深度学习区分器在这些度量标准上都具有明显的优势,采用FNN和CNN结合的候选密钥筛选方案能够将存储复杂度有效降低.
4 总结与展望
本文分别基于FNN和CNN 2种深度学习模型对减轮SIMON32/64的安全性进行了分析.实验结果发现:CNN构造的区分器在准确率上要优于FNN;对于6,7轮的SIMON32/64该区分器都能够以很高的概率将密文对和随机数据区分开;在利用FNN和CNN区分器共同参与的候选密钥筛选策略中,不但成功缩减了候选密钥可能的范围,而且有效降低了攻击复杂度、数据复杂度及时间复杂度.这也进一步说明了通过结合神经网络和差分对一些轻量级分组密码进行安全性分析是一个可行的手段.另一方面,能否利用机器学习中的其他算法来构建分组密码的新型区分器,有待进一步研究.

