磁致伸缩发射换能器的有限元设计建模
中国船舶第七一五研究所 孙昕煜 范进良
本文介绍了磁致伸缩声学发射换能器的有限元设计需求,给出了一些典型有限元计算的设计参数,探讨了声学设计的参数选择和振子磁学设计问题,给出实例对声学有限元设计和磁学有限元设计的有效性进行了验证。
压电陶瓷发射材料(如锆钛酸铅陶瓷PZT-4),具有在电场的作用下发生形变的功能(称之为压电效应),因为材料具有应变适中、结构坚固、形状多样、制作工艺成熟等特点,是目前应用最为广泛的声学发射换能器材料。磁致伸缩材料(如铽镝铁TbDyFe,国外称之为Terfenol-D;铁镓FeGa,国外称之为Gafenol)是一种智能驱动材料,具有在磁场的作用下发生形变的功能(称之为磁致伸缩效应或压磁效应),尤其是铽镝铁TbDyFe材料,因为具有应变大、声速低等特点,在低频声学发射换能器、致动器等领域有广泛应用。
目前,利用有限元软件ANSYS、ATILA等,可以方便的计算结构多样的声学换能器。相比压电材料的形状多样化,磁致伸缩材料形状较为单一,一般为纵向耦合形式(其应力、应变和磁场方向沿纵向Z方向)。在有限元软件ANSYS中,利用压电耦合场单元模拟压电陶瓷材料,可方便计算压电陶瓷声学换能器,但并未提供压磁耦合单元,这给磁致伸缩声学发射换能器有限元设计建模带来了困难;国内莫喜平提出采用压磁-压电比拟的方法,通过等效方法(磁学量与电学量等效、磁弹常数与电弹常数等效)以及广义位移(激磁安匝数)、广义力(磁通量),可以计算磁致伸缩换能器的发送电流响应、方向性、动态阻抗等参数。
由于压电材料的性能研究较为充分,国内外材料性能大体一致,可以获得详细的材料设计参数,这对压电换能器的有限元设计提供了便利;由于磁致伸缩材料的性能与其工作状态(磁化状态、应力状态)以及材料的制作工艺密切相关,国内外材料性能差异较大,国外特定条件下的材料参数可提供一定借鉴,由于缺乏设计所需的国产材料的完整参数,这对利用国产磁致伸缩材料进行发射换能器的精确有限元设计带来了困难。
与压电换能器设计又一不同之处体现在磁致伸缩发射换能器有限元设计中,需要解决的是振子的磁路设计,以确定合适预应力条件下的偏磁磁场分布、驱动磁场分布。
1 纵向耦合线性方程
以TbDyFe为例,对于纵向耦合模式,忽略非线性,材料具有如下线性方程形式:
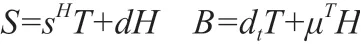
式中纵向方向为磁化方向、预应力方向(假设为z方向,即3方向),dt为d的转置矩阵;方程中S、T、B、H分别为应变、应力、磁通密度、磁场强度;方程中恒磁场条件下弹性柔顺系数sH、压磁应变系数d、恒应力条件下导磁系数μT具有张量形式。
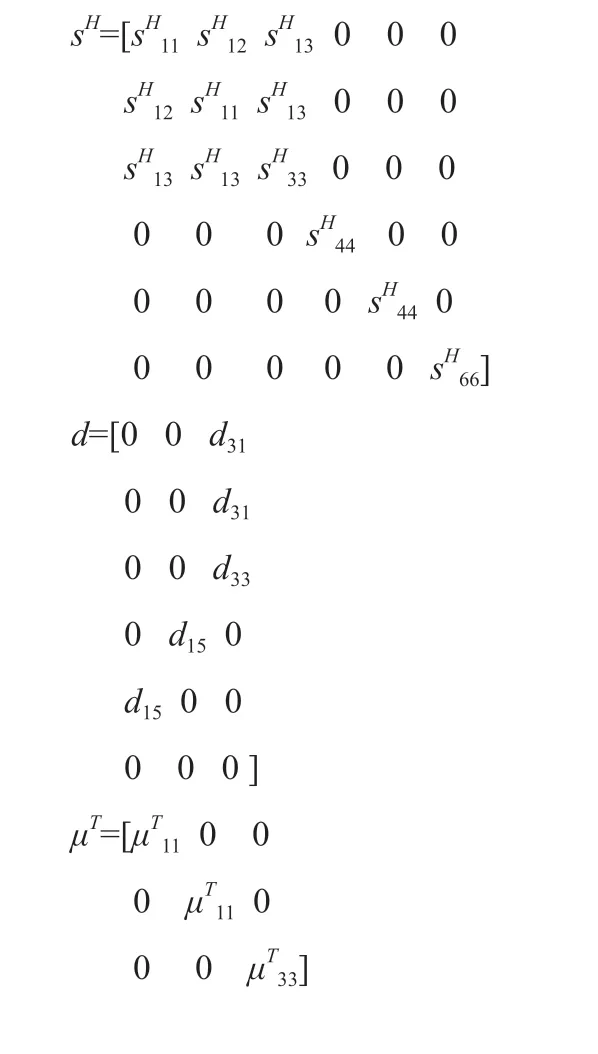
2 压电压磁类比
以PZT-4为例,对于纵向耦合模式,忽略非线性,材料具有如下线性方程形式:

式中纵向方向为电极化方向、预应力方向(假设为z方向,即3方向),dt为d的转置矩阵;方程中S、T、D、E分别为应变、应力、电通密度、电场强度;方程中弹性柔顺系数sE、压电应变系数d、恒应力条件下介电系数εT具有张量形式。


表1 压电材料与压磁材料性能对比(Z轴方向极化)
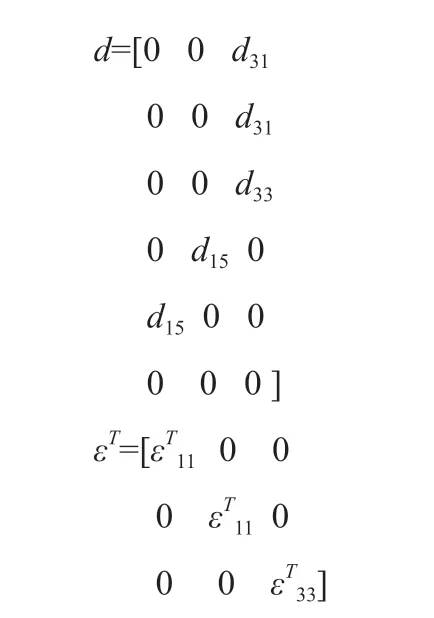
比较TbDyFe和PZT-4材料的线性方程(本构关系),可将Tb-DyFe的S、sH、T、d、H、B、μT分别与PZT-4的S、sE、T、d、E、D、εT等效,从而在有限元软件ANSYS中可利用耦合场压电单元模拟计算压磁材料。
3 有限元计算的设计参数
3.1 声学设计参数
为了方便建模,表1给出了压电材料与压磁材料性能对比(Z轴方向极化),ε0、μ0分别为真空介电系数、真空导磁率(表1)。
按照有限元软件ANSYS计算磁致伸缩发射换能器,其一般流程同压电换能器,对于压磁材料、压电材料还需要将ANSI/IEEE压电标准pp176-1987中3-D张量对应角标顺序x、y、z、yz、xz、xy的参数,按照ANSYS参数输入顺序x、y、z、xy、yz、xz进行输入,并按照ANSYS坐标变换规则进行适当变换,建立几何模型、输入材料参数,利用结构单元、压电耦合单元、流体单元并结合无限远吸收边界条件,分割网格、建立水中模型进行声学性能预报。
与压电换能器不同之处是有源材料声学设计参数、电边界条件以及节点参数的定义不一致,在ANSYS中对于压电材料默认输入的是弹性[sE]或刚性[cE]=[sE]-1、压电系数[d]或[e]=[cE]×[d]、介电常数[εs]=[εT]-[e]t×[d];在ANSYS中对于压磁材料默认输入的是弹性[sH]或刚性[cH]=[sH]-1、压磁系数[d]或[e]=[cH]×[d]、磁导率[μs]=[μT]-[e]t×[d]。对于磁致伸缩发射换能器计算出来的一般是发送电流响应,而压电发射换能器计算出来的一般是发送电压响应。
按照表1给出了压电材料与压磁材料性能对比(Z轴方向极化),法国CEDRAT Researche研究人员F.Claeyssen给出的60kA/m偏磁、20MPa预应力条件的参数、以及F.Claeyssen给出了100kA/m偏磁、30MPa预应力条件的参数,可以看出不同条件下磁致伸缩材料参数显示出较大差异性,主要体现在弹性柔顺系数、导磁系数。
3.2 电磁设计参数
TbDyFe材料的电阻率ρe=60e-6Ω.m。对于磁导率的参数选择极为重要,直接关系到磁路设计的方向、量值。相关的国外文献表明,超磁致伸缩材料的相对磁导率范围一般在2~10,美国海军水下武器中心Naval Underwater Warfare Central(简称NUWC)在一种2.5kHz磁致伸缩Tonpilz声纳换能器设计中使用的相对磁导率参数为6、对应的偏磁磁场为60kA/m、偏置磁通密度为0.45T、驱动磁场为±40kA/m、预应力为25MPa;法国CEDRAT Technologies使用的相对磁导率参数为4、对应的偏磁磁场为1000Oe、预应力为40MPa;加拿大Defence Research Establishment Atlantic(简称DREA)使用的相对磁导率参数为4.5、预应力为25MPa;英国BAe-SEMA Ltd.使用的相对磁导率参数为3.5、预应力为15MPa。

表2 法国Terfenol-D样品带偏场和预加应力下的纵向模态系数
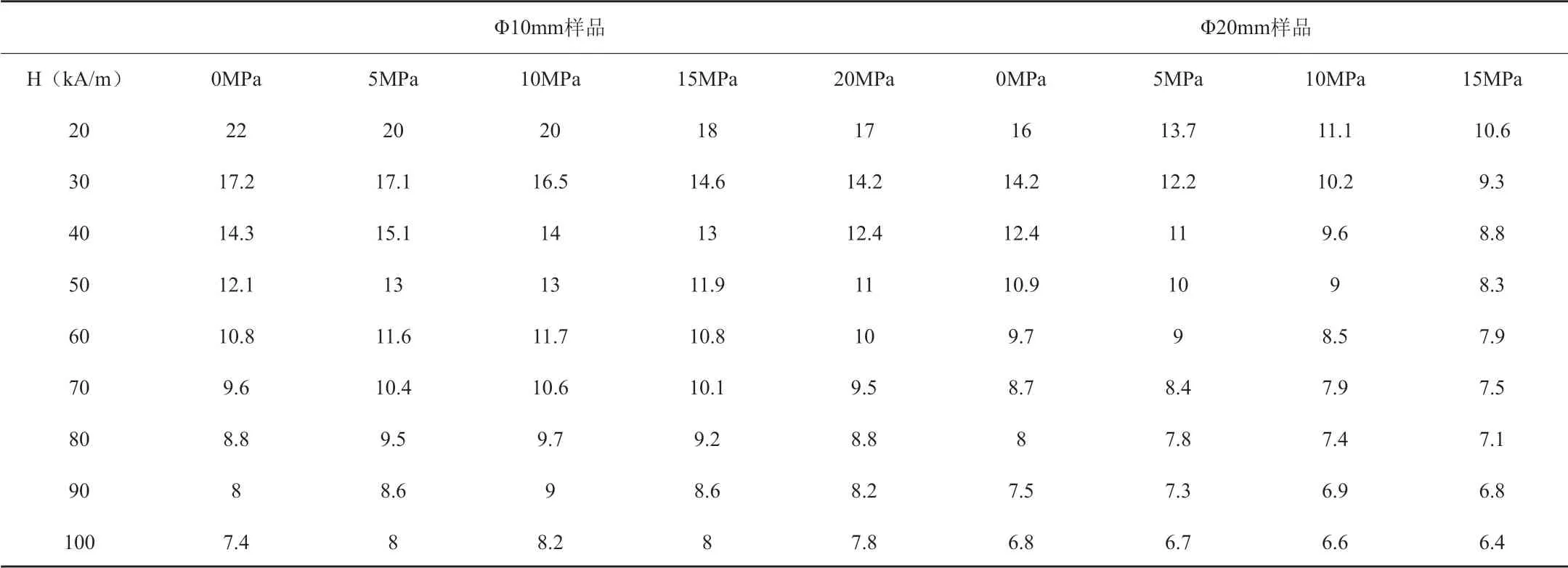
表3 国产TDT-110磁致伸缩样品相对磁导率

表4 声学2-D有限元模型的单元类型
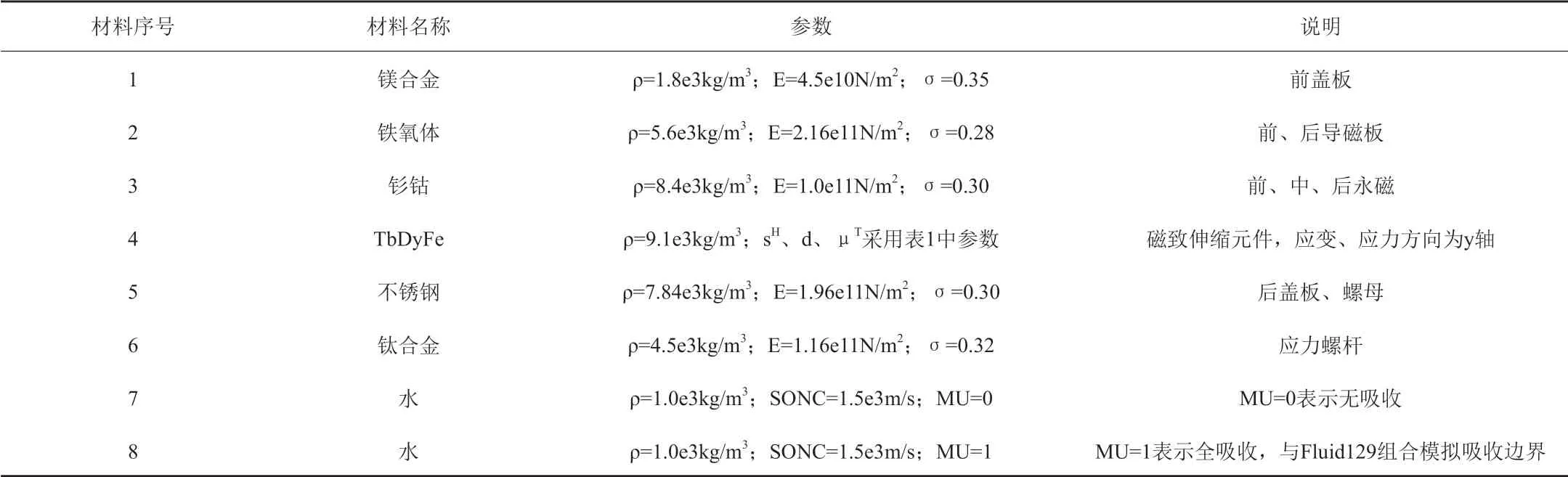
表5 声学2-D有限元模型的材料参数
对于TbDyFe材料,最大可用交流场一般在偏磁磁场的80%左右,最大可用应力一般在机械预加应力的80%左右。
根据上述分析,国外Terfenol-D样品相对磁导率范围为4.3~6~8.4、偏置磁场范围为100~60~31kA/m、偏置磁通密度为0.54~0.45~0.33T、预加应力范围为40~21~15MPa。
表3给出了对国产TbDyFe磁致伸缩样品(牌号TDT-110)相对磁导率的测试,结果表明磁导率与磁场、预加应力密切相关,相对磁导率随磁场、预加应力的增加而下降,因此磁路设计需要根据材料的具体性能进行工作点选择。
磁路设计常用的方法有磁导法和有限元法。磁导法在扬声器磁路设计中应用较多,对于声学换能器的磁路设计,为计算精确,一般可利用ANSYS Emag、Ansoft Maxwell、FLUX、Infolytical Magnet等有限元软件,建立电磁场有限元模型(静磁场、涡流场、瞬态场),代入永磁材料参数(电阻率、磁性能、磁化方向)、软磁材料参数(电阻率、磁化性能)、其他导磁材料参数(电阻率、磁化性能)和加载,进行计算区间磁学性能预报。通过磁路的设计,可获得磁致伸缩材料内部的偏磁磁场分布,给定激励条件下驱动磁场分布以及磁路内部的磁饱和情况、磁力线分布等,以检验磁致伸缩材料工作点符合性。

图1 一种2.5kHz磁致伸缩材料纵向换能器的结构、模型计算与测试比较

图2 纵向换能器的ANSYS有限元模型、发送电流响应计算

图3 纵向换能器压磁振子的磁力线计算、磁场强度计算(FLUX2D有限元模型)
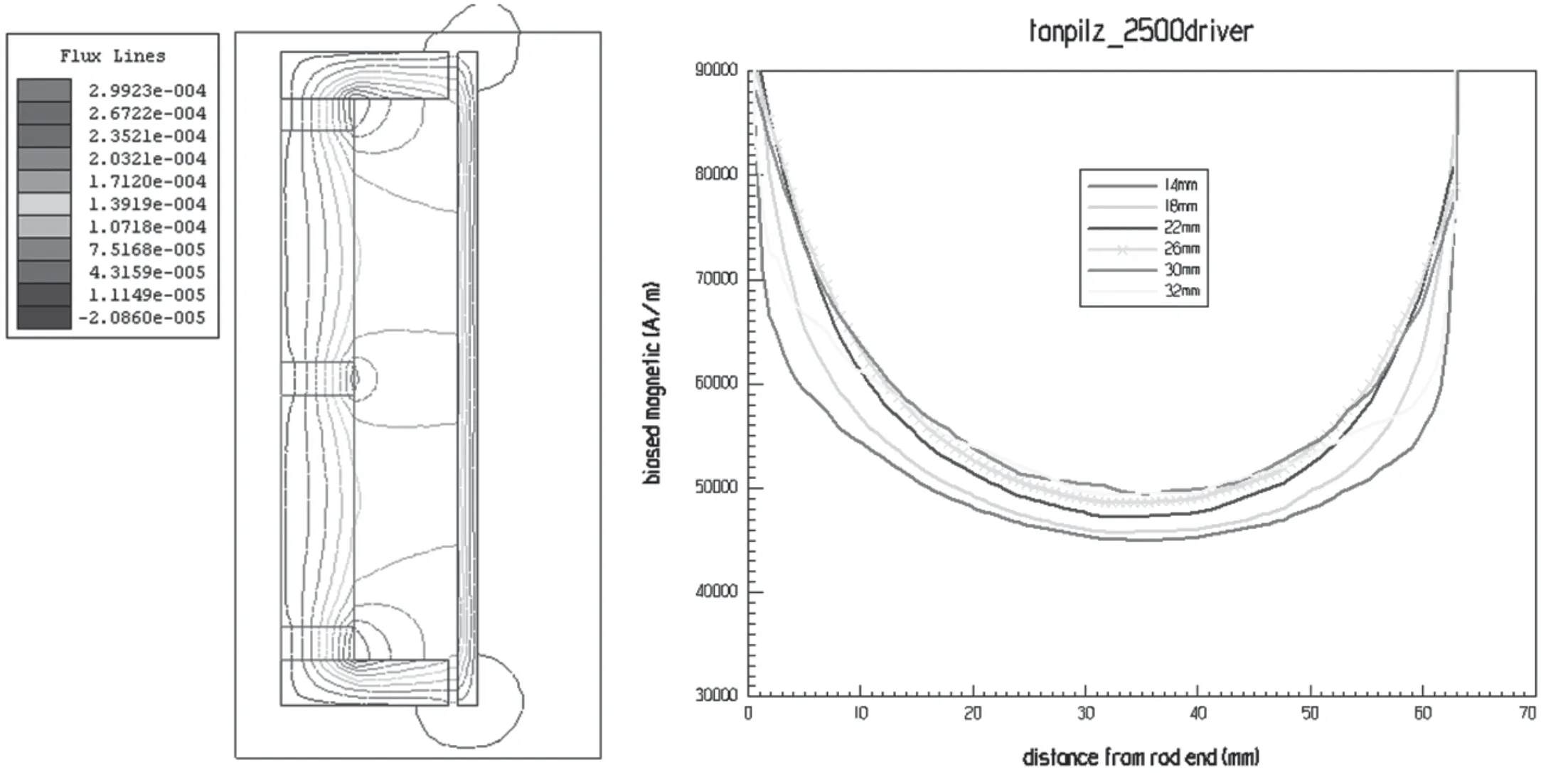
图4 纵向换能器压磁振子的磁力线计算、磁场强度计算(MAXWELL2D有限元模型)

表6 静磁学2-D有限元模型的材料参数
3.3 有限元计算与验证
3.3.1 声学有限元计算
图1所示为一种磁致伸缩材料纵向换能器的结构,利用ATILA进行有限元建立的模型计算与测试比较。
利用ANSYS软件建立的2-D有限元轴对称模型,使用的单元类型和材料参数如表4、5所示,计算了换能器的发送电流响应如图2所示,在核心工作频带2kHz~5.5kHz内有明显的两个谐振频率,有效地展宽了频带,计算的谐振频率、频响起伏等结果与图1吻合性良好。
3.3.2 磁学有限元计算
图3所示为利用FLUX2D静磁学有限元模型,进行的纵向换能器压磁振子的磁力线计算、磁场强度计算结果;图4所示为利用MAXWELL2D静磁学轴对称有限元模型,进行的纵向换能器压磁振子的磁力线计算、磁场强度计算结果,计算使用的材料参数如表6所示;两者吻合性良好。
3.3.3 计算讨论
在利用ANSYS进行磁致伸缩换能器有限元声学性能计算时,一般忽略了材料固有的磁化参数B(H,T)、应变λ(H,T)、杨氏模量Y(H,T)等非线性的影响,使得实际动态状态下材料参数与建模选择参数有一定偏差,这是造成磁致伸缩换能器计算结果(谐振频率、发送电流响应等)与测试性能偏离的主要原因。再者,上述声学计算中,忽略了磁路的退磁场和漏磁的影响,使得计算时施加到元件内的有效磁场偏大,导致计算的发送电流响应比测量值偏大。
总结:本文介绍了磁致伸缩发射换能器的有限元设计需求,给出了一些典型设计参数,探讨了声学设计的参数选择和振子磁学设计问题,给出了实例对声学有限元设计和磁学有限元设计的有效性进行了验证。

