基于改进NSGA-Ⅱ算法的FCC分离系统多目标优化

魏彬，周鑫，王耀伟，郭振莲，陈小博，刘熠斌，杨朝合

（1中国石油大学（华东）化学工程学院，山东青岛266580；2山东京博石油化工有限公司，山东滨州256600）

引 言

催化裂化是重油轻质化的重要手段，2018年我国加工能力已超过2.2亿吨[1]。催化裂化主要产品液化气、汽油是装置经济效益的主要来源[2-3]，其产品质量与收率除了与原料性质、催化剂性能、反应条件有关外，还受分离系统关键操作变量与效率的影响。分离系统由于其物流和能流的循环交错，以及众多的可调节操作变量，炼厂对催化裂化装置的优化操作变得复杂、困难[4]。因此，要实现装置效益最大化，需对分离系统多个目标同时进行优化，仅仅根据生产与工程经验是远远不够的。

随着计算机技术的发展，越来越多的研究人员应用过程模拟软件对石油化工过程进行模拟与优化。庞利敏等[5]应用Aspen Plus对金陵石化催化裂化装置分离系统进行了操作参数优化，提升了汽油收率与干气的品质；田涛[6]运用PRO/Ⅱ对FCC主分馏塔的取热分布进行优化分析，得出取热分布对气液相负荷以及产品产量与质量的影响；全瀛寰等[7]应用Aspen Plus对独山子石化催化裂化装置吸收稳定系统相关工艺参数进行优化，降低了干气C3+含量；雷杨等[8]运用PRO/Ⅱ对FCC吸收稳定系统的系统能耗和吸收效果进行优化，降低了系统的冷热负荷；韩祯等[9]利用PRO/Ⅱ从单因素和双因素角度分析了吸收稳定系统能耗的影响因子，初步探究了经济性最优的吸收稳定系统低温节能工艺。上述研究工作均以某个目标作为优化对象。生产装置的经济效益取决于目的产物的收率、产品质量、能耗等多个因素，在某一因素最优的情况下，其他的因素并不一定处于最优条件，因此单目标优化得出的最优操作条件往往是片面的，极有可能造成“因小失大”的局面。从实际效果上看，单目标优化工作就失去了其优化本身的意义。

近年来，通过引入优化算法来实现石油化工过程的多目标优化，受到了许多研究人员的青睐。非支配排序遗传算法（NSGA-Ⅱ）[10]作为目前最流行的遗传算法之一，不少研究人员通过建立数学优化模型，运用NSGA-Ⅱ对优化模型进行求解，得到Pareto解集，实现石油化工过程的多目标优化[11-15]。在遗传算法中，算法参数在整个优化求解计算过程中起到至关重要的作用[16]，而研究人员在运用算法时往往忽略了这一点，仅给定一套固定的整定参数，这对优化过程的准确度与求解效率均有着不可忽视的影响。

针对上述存在的问题，本文以某石化65万吨/年重油催化裂化装置生产数据为基础，通过HYSYS对催化裂化装置进行更详实全面的全流程模拟。以汽油、液化气收率与分离系统能耗为目标函数，以产品质量为约束函数，通过灵敏度分析选取8个关键操作变量，建立数学优化模型。搭建HYSYS与MATLAB集成平台，运用改进的NSGA-Ⅱ对优化模型进行求解，选取最佳遗传代数下的Pareto前沿并确定其最优解，最终得到最优解所对应的优化操作变量。希望通过所建立的多目标优化方法能为催化裂化装置分离系统的操作变量优化提供重要的数据支持与参考。

1 催化裂化全流程模拟

以某石化65万吨/年重油催化裂化装置生产数据为建模基准并结合该厂装置流程，应用HYSYS搭建催化裂化全流程稳态模拟模型，物性方法选择PENG-ROB[17]，其中主分馏塔物性方法选择BK-10[18]。催化裂化工艺流程如图1所示。

1.1 模型搭建

催化裂化装置流程由反应-再生系统、分离系统以及辅助设备组成。HYSYS催化裂化模块内置21集总动力学模型[19]，首先输入该装置的原料性质、催化剂、设备参数、操作参数等数据，采用默认的反应动力学参数进行初始化模拟。该装置反应进料为70%的常压渣油掺炼30%的常压蜡油与焦化蜡油。从沉降器来的高温反应油气进入主分馏塔T101，经过分离得到塔顶出料为粗汽油和富气混合物，侧线汽提塔T101-1采出为轻柴油，塔底产物为油浆；吸收塔T201进料为粗汽油和压缩富气以及稳定塔T204来的补充吸收剂，塔顶出料为贫气，塔底出料为富吸收汽油，与压缩富气和解吸塔T202塔顶来的解吸气混合进入闪蒸罐；解吸塔T202的作用是将来自闪蒸罐的凝缩油进行解吸，出料为脱乙烷汽油去稳定塔；再吸收塔T203进料为贫气和主分馏塔来的部分轻柴油，塔顶产物为干气，塔底产物为富吸收油返回主分馏塔；稳定塔T204进料为脱乙烷汽油，塔顶产物为液化气，塔底产物为稳定汽油。该装置在0回炼比的情况下运行，因此模型不设置回炼油循环。整个分离系统存在吸收塔塔底富吸收汽油、再吸收塔塔底富吸收油、解吸塔塔顶解吸气、稳定塔部分稳定汽油作再吸收剂4个循环。

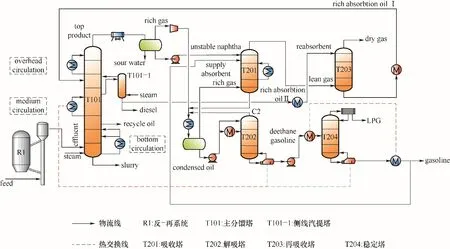
图1 催化裂化工艺流程Fig.1 Simulation diagramof FCCprocess

1.2 模型验证

为建立符合装置生产数据的反应-再生系统模型，需建模后在HYSYS催化裂化模块中输入产物详细分布及性质，对反应-再生系统模型动力学参数进行校准[20]，校准结果如表1所示。分离系统重要操作参数模拟值与标定值对比如表2所示，可以看出，模拟值与标定值的相对误差都在可接受范围内。图2为催化裂化产品质量收率模拟值与标定值的误差图，要素点都在准线上，说明相对误差小；图3为粗汽油与轻柴油ASTM D86模拟值与标定值的误差图，除初馏点外，要素点都靠近准线或在准线之上，说明模拟结果较为准确。另外，产品质量控制指标如表3所示，从表中可以看出产品质量合格，均在指标范围之内。由以上数据可以看出，整体模拟值与标定值的吻合度较高，说明模型准确程度高，可用于下一步的优化工作。

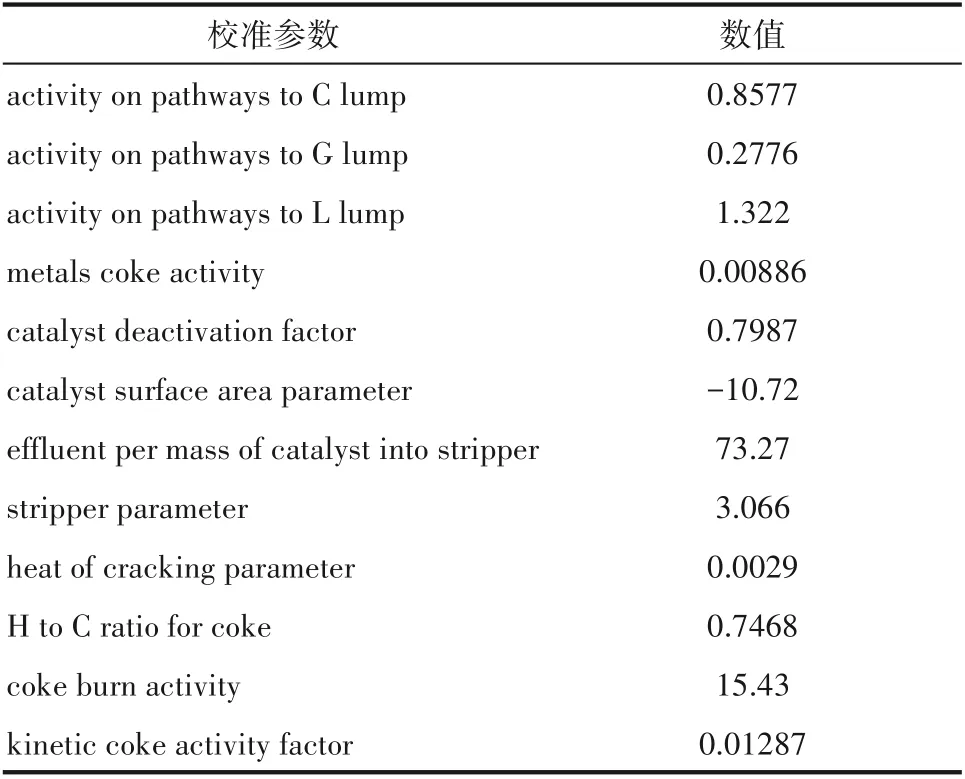
表1 催化裂化模型校准参数Table 1 Calibrated parameters of FCC model

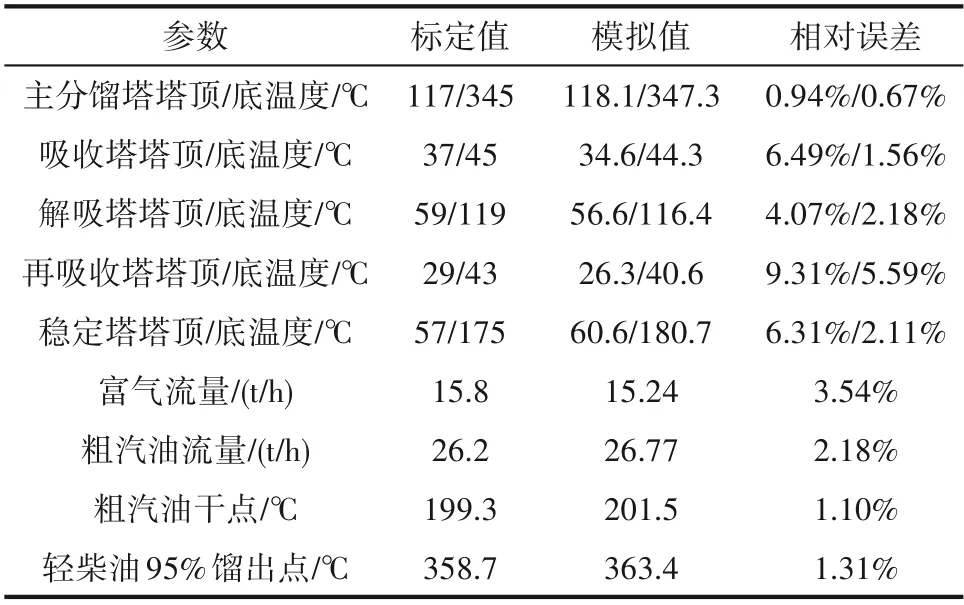
表2 分离系统重要操作参数的模拟值与标定值的数据比较Table 2 Comparison between simulated and working values of the important parameters of the separation system

2 催化裂化分离系统多目标优化

2.1 多目标优化模型的建立

优化模型包含目标函数、约束函数与决策变量，优化模型的建立过程如下。

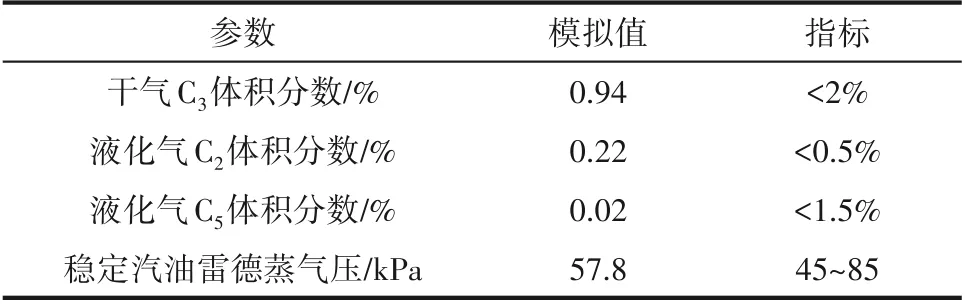
表3 产品质量控制指标Table 3 Indicators of products quality control

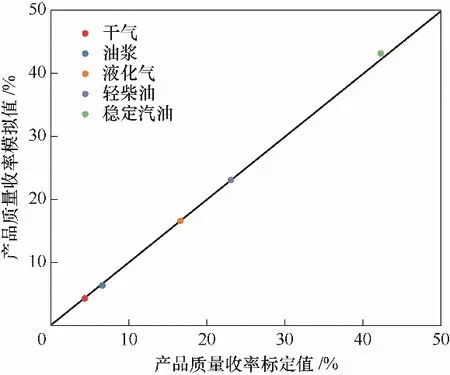
图2 催化裂化产品质量收率模拟值与标定值的误差Fig.2 Error of FCCproducts yield simulated and working values

（1）目标函数 该厂重油催化裂化装置生产方案为多产汽油、液化气，目的产品收率对装置效益影响最大，分离系统能耗对装置效益也有着重要影响。本文将汽油、液化气的收率之和作为第一目标函数，以分离系统能耗作为第二目标函数。总能耗包括了图1中所有耗能设备，其中主分馏塔一中循环与解吸塔塔底再沸器、稳定塔塔底再沸器存在热交换，且部分凝缩油进料与作为再吸收剂循环的稳定汽油也存在热交换，即对总能耗来说减少了等量的冷、热耗，其换热情况如图1所示，故总能耗计算如式（1）所示，目标函数如式（2）所示。

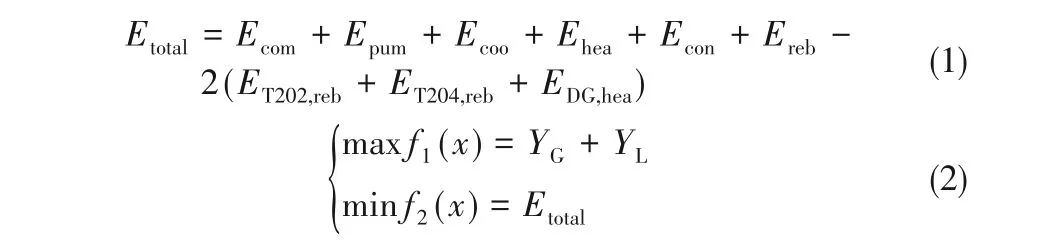
（2）约束函数 根据装置生产要求，约束函数如式（3）所示。

（3）决策变量 该装置分离系统可调节关键操作变量一共有11个，如表4所示。为了探究这些可调节操作变量对汽油、液化气的收率之和与分离系统能耗的影响程度大小，本文对这11个可调节操作变量进行±10%的灵敏度分析，结果如图4所示。

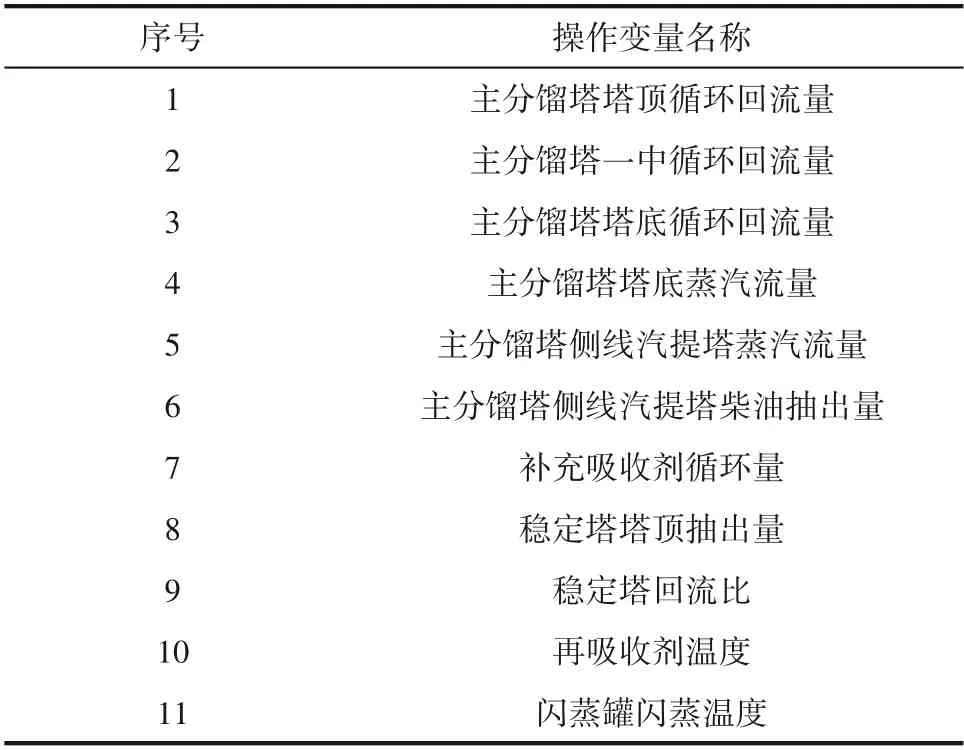
表4 可调节操作变量Table 4 Adjustable operating variables

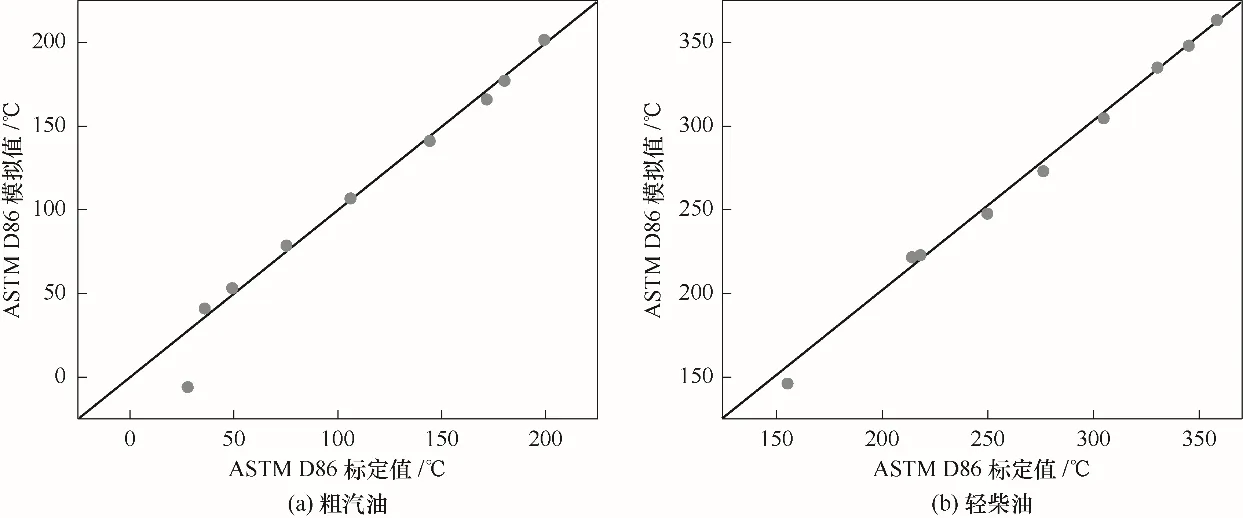
图3 ATSM D86模拟值与标定值的误差Fig.3 Error diagrams of simulated and working values of ATSMD86

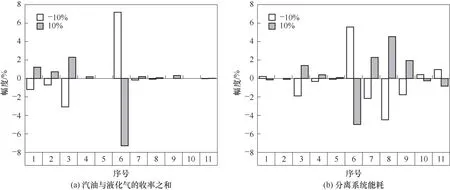
图4 灵敏度分析Fig.4 Sensitivity analysis

图4表明，主分馏塔塔底蒸汽流量、侧线汽提塔蒸汽流量以及再吸收剂温度对两个目标函数的影响微乎其微，而其他8个操作变量都分别对目标函数存在不同程度的影响，因此本文选择这8个可调节操作变量作为此优化模型的决策变量，根据实际生产数据和装置设计余量，确定操作变量范围，如表5所示。

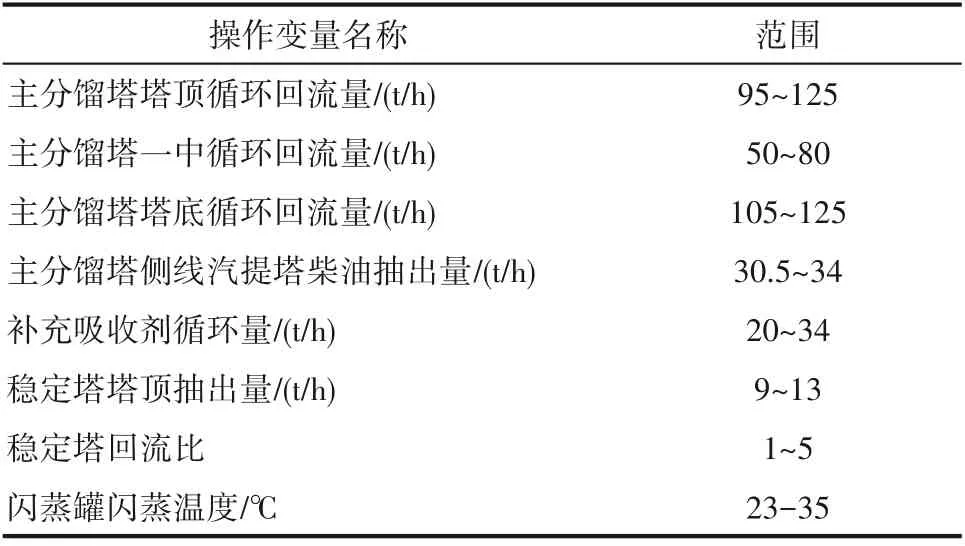
表5 决策变量及其范围Table 5 Decision variables and their scope

2.2 改进的非支配排序遗传算法的参数设定

在MATLAB软件中，通过串联基于COM技术的Actxserver函数的HYSYS接口，搭建MATLAB与HYSYS集成平台[21]，并引入改进的NSGA-Ⅱ算法对优化模型进行求解，模型求解计算过程概念框图如图5所示。根据算法原理以及计算过程概念框图可知，种群规模、遗传代数、交叉概率Pc、变异概率Pm的参与始终为循环计算的必经步骤，且在模型计算前必须确定这些参数才能进行计算[22]。另外，多次计算求解表明这些算法参数的设定取值对优化模型求解过程的影响不容忽视，表明原算法的固定参数策略不足以体现此算法的优越性。因此对NSGA-Ⅱ的算法参数进行讨论与设定，并运用到多目标优化中。

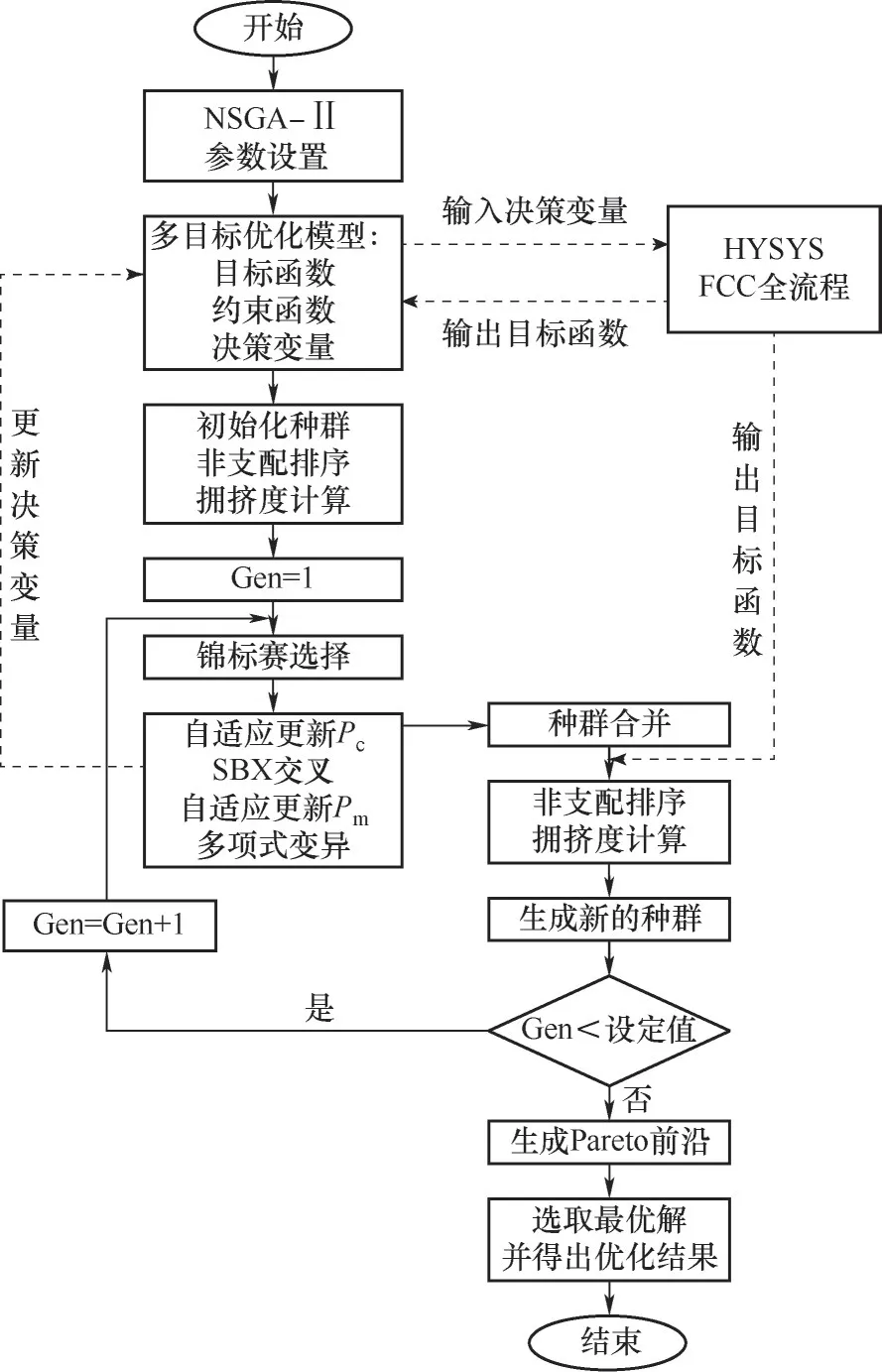
图5 多目标优化计算过程概念框图Fig.5 Conceptual block diagram of the multi-objective optimization calculation process

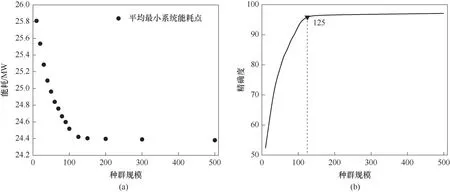
图6 种群规模与能耗关系(a)及种群规模与精确度拟合结果(b)Fig.6 Map of population size versus energy consumption(a)and population size versus precision fit(b)

（1）种群规模 种群规模的大小直接影响种群的多样性和计算的复杂度，其值偏小能缩短计算时间，但算法易过早收敛；偏大能保持多样性，使得Pareto解集分布均匀，但计算时间急剧增加[23]。所以对于具体工程优化问题，选择适合的种群规模是必要的。本文采用李刚等[24]的实验方法，探究适合本优化模型的种群规模。

根据该实验方法，选取最小分离系统能耗目标函数为对象，得到种群规模大小与最小分离系统能耗的关系，如图6(a)所示。依据其实验过程，图6(a)经转化后满足式（4）的函数关系，即该实验定义的求解精度f(x)与种群规模x的函数关系，因此对其进行拟合。求解精度与种群规模的拟合图如图6(b)所示，拟合结果参数如表6所示。其中R-square值表示拟合结果的好坏，值越接近于1表明拟合程度越高，可知该曲线拟合程度较好。

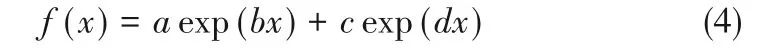
从图6(b)中可以看出，对种群规模在1～125时精确度上升极快，当种群规模超过125后精确度上升缓慢。根据工程要求以及保证计算时间和精度的前提下，采用的种群规模为125。

表6 拟合参数Table 6 Fit parameters

（2）交叉概率Pc与变异概率Pm交叉概率Pc的大小决定种群的丰富程度，同时也影响优良个体的生存；变异概率Pm的大小决定是否能跳出局部值而找到全局最优解，同时又会影响个体的进化[25]。换句话说，采用固定的Pc与Pm会影响算法的收敛性与多样性，进而影响到优化结果的准确度与优化效率，且对于每个优化模型，Pc与Pm的取值不同也会造成不同程度的影响。而Pc与Pm的自适应就能很好地解决这个问题[26]。为了验证自适应策略对于本优化模型的影响，本文采用Pc与Pm自适应策略[27]与固定参数值的优化结果进行对比，确定最适合本优化模型的Pc、Pm，式（5）、式（6）为本文采用的Pc与Pm自适应表达式。使用NSGA-Ⅱ默认的模拟二进制（SBX）交叉算子与多项式变异算子，选择方式为二元锦标赛选择。

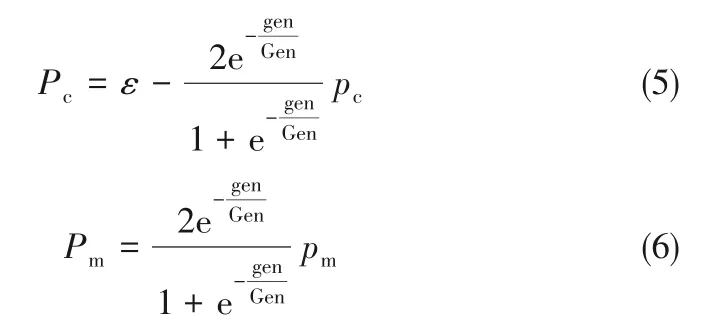
通常情况下，反转世代距离[28]（inverted generational distance，IGD）作为一个综合性能评价指标，用来评价算法的收敛性和分布性能，其定义如式（7）所示。由其定义可知，指标需要真实Pareto前沿，然而在实际问题中，往往无法获取优化问题的真实Pareto前沿。因此，本文提出对不同组参数设置取值分别进行10次相同计算，通过归一化后的平均目标函数值（均一目标）与求解平均计算时间来进行比较算法性能。此方法原理在于从算法实际性能考虑，即优化目标结果值和优化计算时间，将两个目标函数无量纲化进行直观比较，并与计算时间综合考虑，评价其性能。计算初始HYSYS模型设置一致，结果如表7所示。

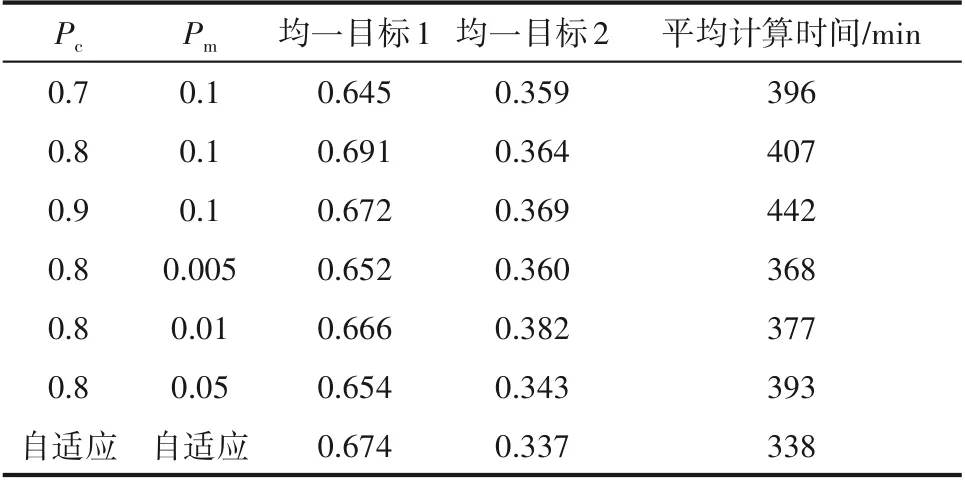
表7 P c、P m对优化的影响Table 7 Impact of P c and P m on optimization

为了探究自适应策略在本模型中是否具有优越性，首先寻找最佳的固定参数设定值，再与之比较。从表7中可以看出，在Pm固定、Pc变动的情况下，当Pc取0.8时，平均汽油、液化气最大收率之和明显大于0.7、0.9，而平均最小能耗与平均计算时间相近；在Pc固定、Pm变动的情况下，当Pm取0.1时,虽然计算时间最长，但其平均汽油、液化气最大收率之和远大于另外三个设定值。因此当Pc取0.8、Pm取0.1时其综合优化性能最佳。将其与Pc、Pm自适应策略对比可以发现，平均汽油、液化气最大收率之和相近，但Pc与Pm自适应策略下的平均最小能耗远小于前者，且计算时间大幅度降低，大大提高优化模型的求解效率。综合分析可知，该Pc与Pm自适应策略符合本优化模型的参数设置。

3 优化结果与分析

3.1 遗传代数的确定

图7展示了不同遗传代数（generation）所对应的Pareto边界图。评价Pareto边界的好坏或者说优化结果是否理想就在于优化点是否分布均匀且连续，并且接近Pareto前沿。从图中可以看出，当遗传代数为200时，Pareto边界图分布均匀，且曲线非常接近Pareto前沿，因此选取遗传代数200下的Pareto前沿曲线作为最优解集。

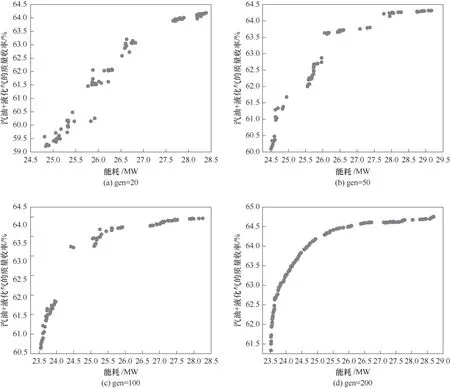
图7 不同遗传代数下的Pareto边界Fig.7 Pareto boundaries under different generation

3.2 Pareto前沿曲线最优点的选取

多目标优化的Pareto前沿曲线上每个点都是一个优化设计点，它们构成一个优化解集。对于本优化模型，随着汽油与液化气的收率之和的增加，能耗必定增大。从多目标优化算法角度看，基于非归一化解法的多目标遗传算法所计算出来的是所有权重组合的最优方案。而在实际工程应用上，需要研究者从中选取一个最优点。

TOPSIS[29]（technique for order preference by similarity to an ideal solution）法又称为优劣解距离法，该方法原理是通过检测评价对象与最优解、最劣解的距离来进行排序。TOPSIS法被广泛用于多目标优化问题Pareto前沿曲线上最优点的选取，在解决工程问题上不失为一种有力的决策方法[30-32]。因此本文采用该方法进行最优点的选取。TOPSIS方法用于选取最优解的步骤：首先将选用的Pareto前沿曲线进行归一化处理[33]，如图8所示；然后根据优化模型选取“理想点”，所谓“理想点”就是同时满足所有目标函数最优情况的点，显然在实际中是取不到的；最后根据欧氏距离公式算出Pareto前沿曲线上的点与“理想点”的距离，如图9所示，以最小距离的点作为该Pareto前沿曲线的最优点。

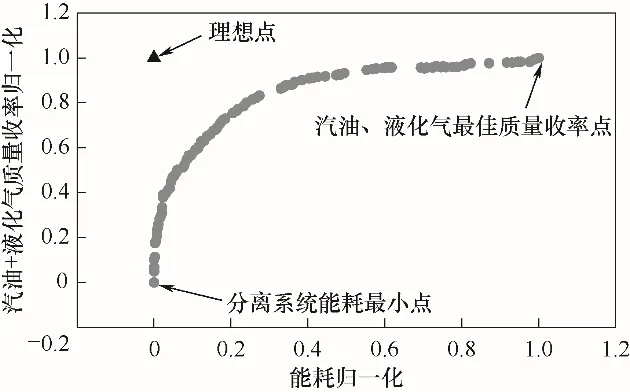
图8 Pareto前沿曲线归一化图Fig.8 Normalized diagramof Pareto frontier

优化结果如图10所示。由图可知，汽油与液化气的收率之和同比提升4.32个百分点，分离系统能耗降低了16.88%，优化效果良好。操作变量调节如表8所示，对于主分馏塔，采取提高顶循回流量，降低一中、塔底循环回流量以及侧线柴油抽出量；对于吸收稳定系统，提高稳定塔塔顶抽出量，降低稳定塔回流比、补充吸收剂量、降低闪蒸罐闪蒸温度，从而达到上述优化效果。

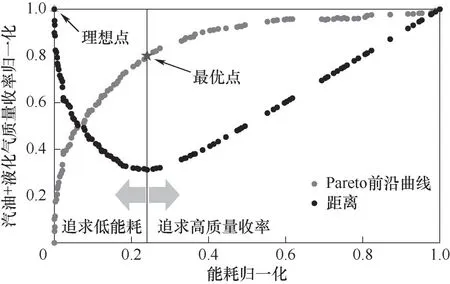
图9 最优解集与理想点的距离图Fig.9 Diagramof the distance fromthe optimal solution set to the ideal point

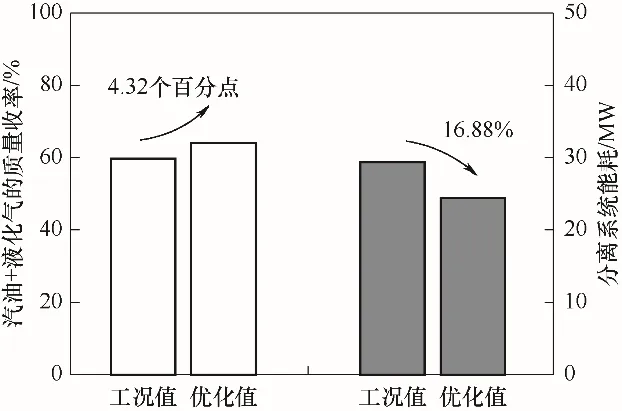
图10 多目标优化结果Fig.10 Diagram of multi-objective optimization results

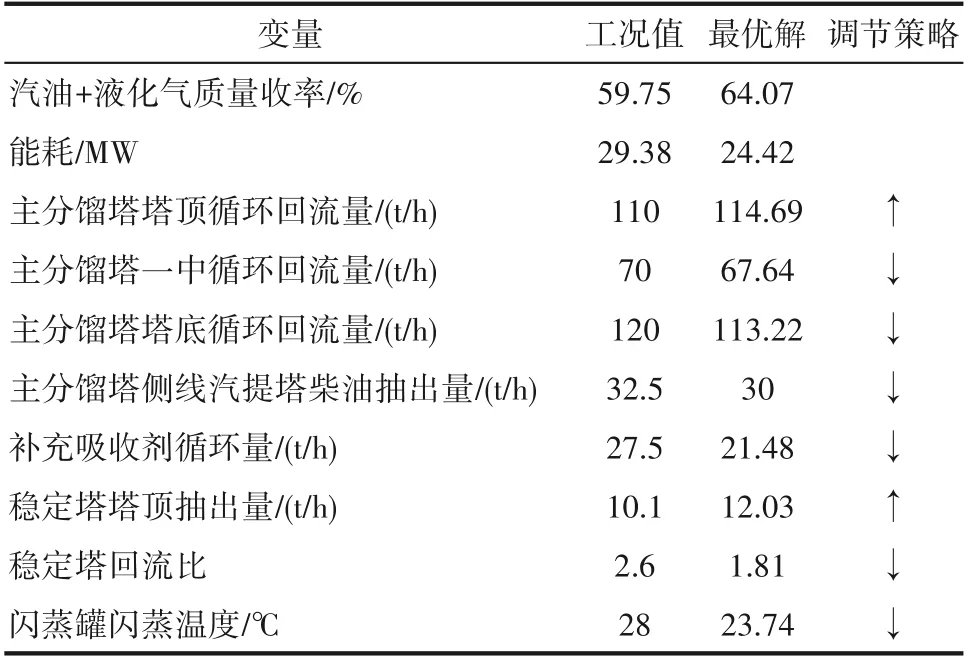
表8 多目标优化结果及最佳操作变量Table 8 Multi-objective optimization results and best operating variables

4结 论

符号说明

C2——液化气C2体积分数,%

C3——干气C3体积分数,%

C5——液化气C5体积分数,%

d——真实Pareto点集个体到获取的Pareto最优点集的欧几里德距离

E——能耗,MW

Gen——总遗传代数

6.3 后期管护（1）用手轻推树干，看苗木根系与土壤是否结合良好，若有明显的裂缝或松动，则说明栽植不到位，应及时补救。（2）观察树坑。土壤疏松有利于根系的萌发，为此，一方面看树坑有无积水，另一方面看浇水后是否松土、有无裂缝要处理。

gen——当前遗传代数

P——真实Pareto点集

|P|——真实Pareto点集个体数

Q——获取的Pareto最优点集

TD——轻柴油95%馏出点,℃

TG——粗汽油干点,℃

v——真实Pareto点集个体

YG——汽油质量收率,%

YL——液化气质量收率,%

ε——自适应参数，本文取1.5

下角标

com——压缩机

con——冷凝器

coo——冷却器

DG——脱乙烷汽油

hea——加热器

pum——泵

reb——再沸器

total——总