气固界面吸附团簇分布及相变机制研究
宋本南,吴春梅,李友荣
(低品位能源利用技术及系统教育部重点实验室,重庆大学能源与动力工程学院,重庆400044)
引 言
气固界面吸附是气体分子在固体表面的相对聚集过程,它是一个典型的表面传热传质过程,也是表面科学中一个重要的研究课题。气固界面吸附是一种常见的自然现象,在许多工程技术领域中大量存在,特别在材料的性能测试[1-2]、废水处理[3-4]、生物医学[5-6]以及储能技术[7]等方面有着广泛的应用。对于平衡态下界面吸附特性的研究,第一步往往是确定吸附等温线,然后再结合吸附理论模型分析吸附过程的本质。1916年,Langmuir[8]基于每个吸附单元只能吸附单个分子的假设提出了著名的Langmuir等温吸附方程,虽然该模型计算得到的吸附等温线末端总是趋于水平,与后来大量实验结果相悖,但Langmuir等温方程的提出为气固界面吸附特性理论研究的蓬勃发展奠定了基础。之后,不同学者分别基于理论分析、数值模拟及经验关联式等提出了多种等温吸附模型,出现了如BET[9]、FHH[10]、AD[11]等一系列经典的多层吸附模型[12],被广泛应用于吸附机理推断、吸附剂比表面积的测定以及吸附性能评价等。但这些理论在吸附量的预测上并不十分成功[13],例如,大量实验结果表明BET理论仅在低压比区有效[14],在高压比区,BET理论预测量远大于实验测量的吸附量。FHH与AD理论在低压区和实验结果有明显的差异,主要适用于较高压力下的吸附预测[15]。之后,研究人员提出了一系列修正模型[15-18],如Redlich-Peterson[19]、Toth[20]等,这些模型成功应用于平衡态下不同压比范围内的吸附量预测。
另一方面,对于非平衡过程,在一定的过冷度下气固界面将发生吸附相变,形成液膜润湿界面。已有大部分研究都将关注点放在了一定过冷度下饱和蒸气在固体表面的凝结成核及其调控,而吸附相变形成机制及相关理论模型却较少涉及。Schlangen等[21]从Gibbs方程出发推导了蒸气吸附和润湿之间的热力学关系,分析了完全润湿及非完全润湿的热力学条件,得到了不同润湿过程中表面张力与界面吸附量之间的耦合关系。Kaplan等[22]指出不同的吸附特性将改变界面的润湿过程,从热力学角度解释了吸附的基本特征,并给出了不同温度下的润湿转变条件。Laaksonen等[23]结合FHH吸附方程和Kelvin方程,提出一种新的非均相成核理论,得到了三种不同的成核机制,即团簇成核、聚结成核和均匀膜成核。Wang等[24]研究了纳米颗粒表面曲率和润湿性对水蒸气凝结的影响,分别探讨了凝结成核的两个阶段,结果指出,水分子团簇的形成可显著提升成核率,粒子表面曲率和润湿性对团簇的生长有着促进作用,但团簇的合并将降低成核率。
目前,已有研究中缺乏从吸附到相变整个过程中界面演化特性的系统研究。无论是经典的BET方程还是修正的AD方程,都不适用于分析吸附相变过程,当吸附平衡压力接近饱和压力时,上述理论计算所得吸附量总是趋于无穷大,在过饱和状态下,界面吸附量为负,显然,这是不符合物理规律的[25-26]。2007年,Ward等[27]首次提出了Zeta等温吸附理论,该模型从统计热力学角度出发,提出了吸附质以团簇形式被吸附在固体表面的基本吸附模式。同时,Wongkoblap等[28]利用Monte Carlo模拟,从微观角度展示了水分子以分子团簇形式吸附在碳表面。Laaksonen[13]结合分子吸附团簇模型,理论预测了过饱和条件下水分子吸附团簇在固体表面冷凝成核特性,模型预测结果与经典非均相成核理论结果吻合很好,然而,Laaksonen并未对冷凝成核前的吸附及团簇演化过程进行阐述。之后,大量的实验研究[29-31]和数值模拟[32]证实了Zeta吸附理论的有效性。为了进一步深入研究气固界面吸附相变过程及其物理机制,本文采用实验测量和理论分析相结合的方法,分析了气固界面吸附特性,明确了吸附层内团簇分布及其演化规律,探讨了界面吸附相变发生条件及其物理机制。
1 实验材料和方法
实验中吸附质为水蒸气,吸附剂分别采用纳米级别二氧化硅及石墨(由徐州捷创新材料科技有限公司提供)。二氧化硅粒径为20 nm,比表面积为(100±25)m2/g,纯度为99.80%,自由水含量小于3%;石墨粉粒径大小为40 nm,比表面积为(90±10)m2/g,纯度为99.95%,自由水含量小于0.2%。吸附测试采用美国Quantachrome公司的Vstar型全自动蒸汽吸附仪进行吸附性能测试。
实验开始前对吸附剂进行预处理,将60~80 mg吸附剂样品分别置于真空干燥箱进行预热与除湿,干燥箱每分钟升温2 K,升温至573 K并维持6 h。之后,设置吸附平衡温度为298 K(精度为0.01 K),开始吸附实验测试。实验过程中当样品腔内压力变化小于±0.11%Psat(饱和压力)时,则认为达到吸附平衡,记录数据,之后通过逐渐升高吸附压力,获取不同压力下吸附量数据,然后不断降低压力,以此获得脱附量。实验压比xV变化范围为0.05~0.9,其中xV=PV/Psat,PV为蒸汽压力。
2 实验结果与讨论
2.1 等温吸附曲线
图1展示了不同压比下水蒸气在二氧化硅和石墨表面的等温吸附量变化情况,可以看出,平衡态下气固界面吸/脱附可逆。在低压比下,石墨表面水蒸气的吸附量缓慢增加,而二氧化硅表面吸附量快速增长。高压比区,吸附量均呈现陡增的趋势。相同压力下,二氧化硅表面的水蒸气吸附量远大于石墨。为了进一步分析界面吸附特性,通常采用一定的吸附理论模型拟合实验数据,获得等温吸附曲线,从而确定界面吸附层内分布特征。如前所述,常见的等温吸附模型包括经典的Langmuir方程[8]、Toth方程[20]、BET方程[9]、AD方程[11]等。Langmuir方程是基于单分子层吸附这一基本假定而提出的,Toth方程是Langmuir方程的扩展形式,可用于多气体吸附体系的描述,BET方程是在Langmuir理论上提出的经典的多层吸附模型。Langmuir方程及BET方程仅在低压比区间与实验数据吻合较好,在中高压比区间误差较大。并且,在压比xV=1(PV=Psat)时,存在奇异点,理论计算所得吸附量趋于无穷大。Anderson等[14]在BET方程的基础上引入了一个小于1的修正参数,提出了AD模型,该模型所预测的吸附量在中高压比区与实验测试结果吻合较好。然而,无论是BET还是AD方程,当xV>1之后,理论计算的吸附量为负值,显然这并不符合物理规律。2007年,Ward等[27]基于统计热力学,提出了Zeta等温吸附理论,其基本模型如下:吸附质以分子团簇的形式吸附在界面吸附位点,一个吸附位点最多只能吸附一个团簇,每个团簇含有ζ个分子,单个团簇所含最大分子数为ζm,每个团簇均可看作量子谐振子,其能量大小和团簇所含分子数相关。由谐振子特性可知所有被吸附气体分子总能量E可表达为[33]:
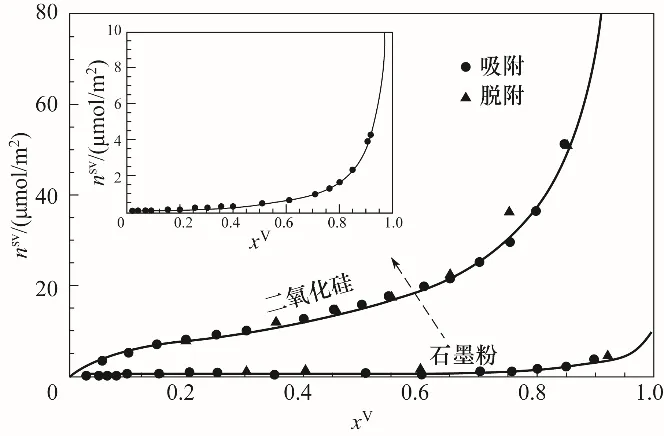
图1 等温吸附曲线Fig.1 Adsorption isotherms of water vapor on silica and graphite surfaces

式中,A为吸附剂表面积,M表示单位面积上的吸附单元数。在此基础上可得到配分函数:
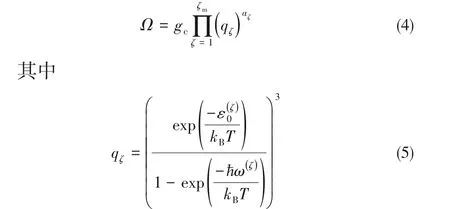
式中,kB表示Boltzmann常数。
根据配分函数与Helmholtz自由能的对数关系可得化学势的表达式:
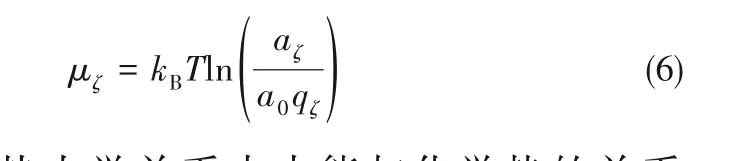
再由一般热力学关系中内能与化学势的关系式,可得ζ个分子的团簇数量aζ的表达式:

由式(10)可知,在一定的压比下,吸附量nSV取决于四个参数:M,c,α和ζm。其中,c与α是只依赖于温度的单值函数,与压力变量无关。而M为界面吸附单元数量,仅与吸附剂材料有关,ζm为团簇所含的最大分子数量,与吸附剂与吸附质之间的作用强度有关。结合实验所测不同压比下的吸附量,可确定M,c,α,ζm四个参数的具体数值,如表1所示。再将等温参数代入式(10),可得吸附曲线,如图1所示,在不同压比区间内,理论吸附曲线和实验测量值吻合很好,对于石墨-水蒸气以及二氧化硅-水蒸气界面,采用式(11)计算所得相对误差分别为0.42%和1.01%。
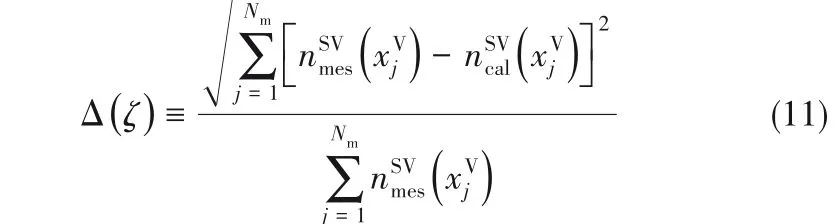

表1 Zeta等温吸附参数Table 1 Zeta isothermal parameters
2.2 团簇分布及吸附相变
为了进一步探讨气固界面吸附特征,分析了界面吸附团簇的演化过程。吸附剂表面吸附单元数M也可通过分子团簇及零吸附单元数量来确定,即:
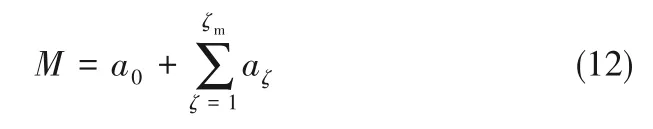
式中,a0表示零吸附单元数量。将式(7)代入到式(12)中可得:
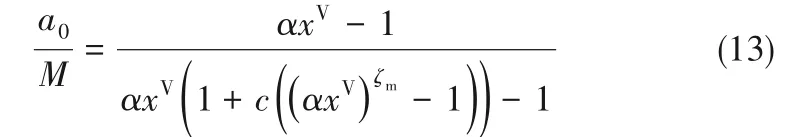
将表1所列参数值代入式(7)和式(13),可得不同压比下零吸附单元与吸附团簇的分布及其演化情况,如图2和图3所示。当压比为零时,气固界面不存在吸附行为,吸附界面被零吸附单元所占据。随着压比的增大,气体分子被吸附在固体表面,零吸附单元数不断减小,与此同时,单分子团簇a1数量不断增加。随着压比的进一步增加,团簇类型增多,单分子团簇所占比例逐渐降低,这一规律与Wongkoblap等[28]的分子模拟结果吻合。对比图2和图3可以发现,对于不同的吸附剂,界面上零吸附单元数量下降的速率以及分子团簇的变化速率是不同的。对于水蒸气-二氧化硅界面(图2),当压比为0.2时,零吸附单元数所占比例已降至20%,大多数吸附单元被单分子团簇占据,所占比例为64%,当压比接近0.9时,零吸附单元几乎全部消失,吸附单元被不同类型的分子团簇所占据。而对于水蒸气-石墨界面(图3),同样在压比为0.2条件下,零吸附单元数为63%,这是由于二氧化硅和水分子界面,二氧化硅中的氧原子易与水分子中的氢原子形成氢键,而石墨与水分子之间通过范德华力相互作用,因此,二氧化硅-水界面气固相互作用强度高于石墨-水界面[34],因此,吸附行为开始瞬间,二氧化硅表面零吸附单元下降速率更快,相同压力下,二氧化硅表面的吸附量大于石墨。
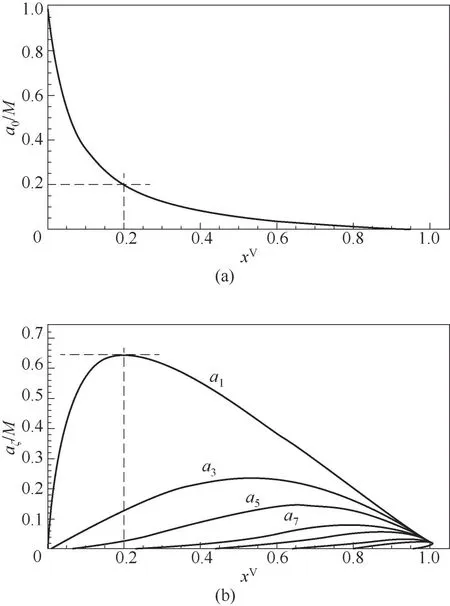
图2 二氧化硅表面零吸附单元(a)及团簇(b)分布演化过程Fig.2 Empty adsorption sites(a)and cluster distribution(b)for water vapor adsorption on silica
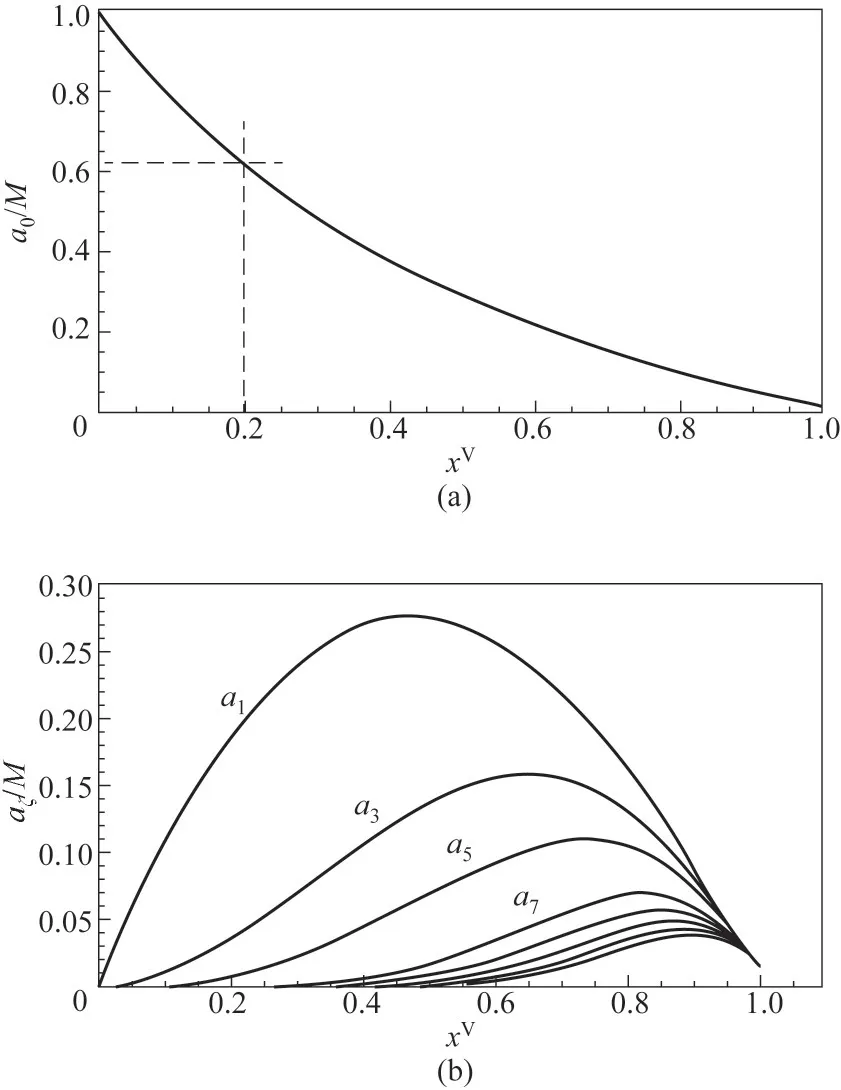
图3 石墨表面零吸附单元(a)及团簇(b)分布演化过程Fig.3 Empty adsorption sites(a)and cluster distribution(b)for water vapor adsorption on graphite
图4给出了饱和压力附近区间内吸附团簇分布及其演化过程。可以看出,当压比略小于1/α时,小分子团簇的数量急剧下降,大分子团簇数量占比逐渐上升。结合式(7)可知,当压比xV=1/α时,aζ/M=1/ζm,即吸附界面上各种类型的团簇出现的概率相同。随着压比的进一步增加,大分子团簇占比急剧上升,界面上小分子团簇几乎消失,当压比为1.14时,大分子团簇数量占比为91%,这些大分子团簇性质均一,具有类液膜的特点,如图5所示。
为了进一步探讨较大压比区间界面吸附特征,将等温吸附曲线拓展至xV>1的近平衡区域,如图6所示。可以看出,当压比xV=1.0,即饱和压力下,Zeta吸附模型计算所得吸附量为一有限值。在xV=1/α附近,吸附量随压比的增加而陡增,当压比进一步增大至某一临界值,吸附量变化逐渐趋于平缓。图7给出了界面吸附量变化率(即∂nSV∂xV)随压比的变化规律,结果表明,初始时刻,零吸附单元迅速下降,单分子团簇陡增,占据吸附单元,此时吸附团簇中单分子团簇占主导,使得界面吸附量增加率逐渐减缓。当压比达到0.2时,界面被吸附团簇所覆盖,零吸附单元所占比例大大降低,随着压比的增加,含多分子团簇比例逐渐上升,使得吸附量增加率缓慢增大。当压比趋于1/α时,团簇类型增多,吸附量变化率急剧上升,并在1/α处达到极值。当xV>1.14之后,吸附量变化率随压比的增加逐渐趋于零。
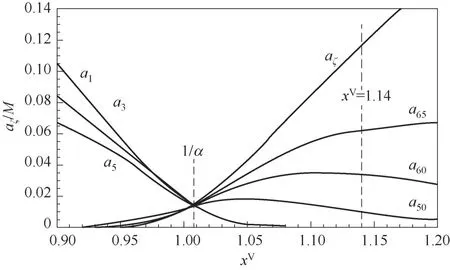
图4 饱和压力附近团簇演化过程Fig.4 Cluster distribution when the pressure is around the saturation pressure
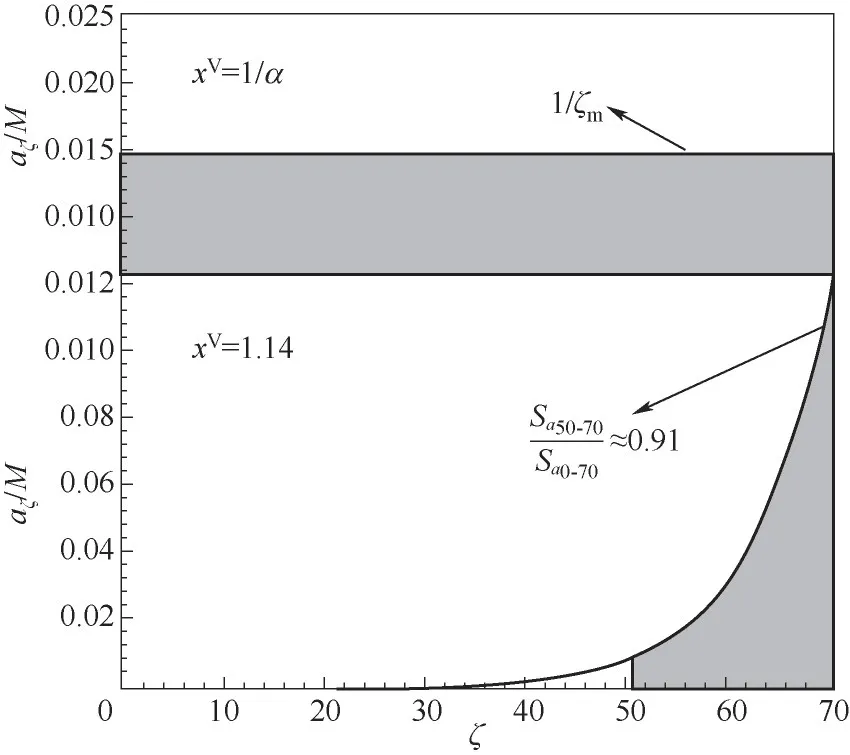
图5 压比为1/α及1.14时不同团簇类型分布Fig.5 The number of different clusters when x V=1/αand x V=1.14
另一方面,由统计热力学可知,Gibbs熵可表示为:
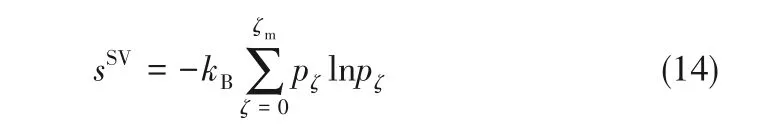
式中,p表示占据第ζ能级的概率,根据Zeta吸附理论的基本思想,pζ=aζ/M,因此,将式(7)代入式(14)可得
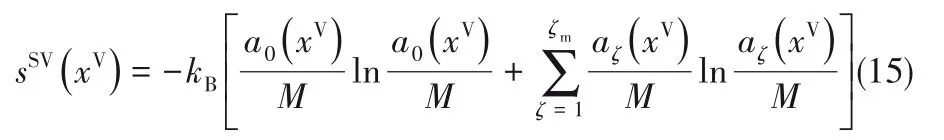
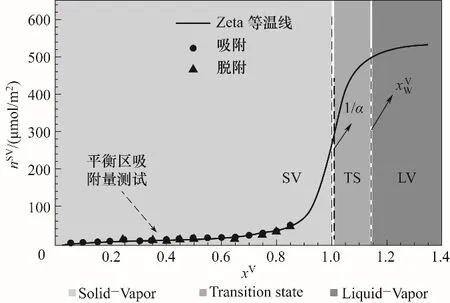
图6 全压比区间Zeta等温吸附曲线Fig.6 Zeta adsorption isothermin the full pressure range
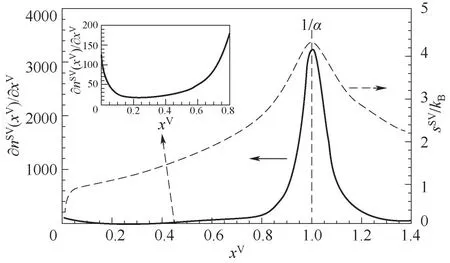
图7 吸附熵及吸附量变化率随压比的变化规律Fig.7 Variations of entropy of adsorption clusters and the adsorption increasing rate with the pressure ratio
图7给出了吸附熵随压比的变化曲线,可以看出,随着压比的增大,出现不同团簇类型的概率增加,系统混乱度增强,熵不断增大。并且吸附熵与吸附量变化率均在压比xV=1/α处达到极值,当压比大于1/α后,熵值不断下降,这证实了在xV=1/α处,气固界面吸附发生了一阶相变[35]。当压比大于1/α时,由于吸附界面存在的是含分子数量相差不大的团簇,团簇种类减少,吸附熵随之减小。
2.3 表面张力
由Gibbs方程可知,气固界面张力γSV与吸附量满足:

结合式(16)~式(18)可得:
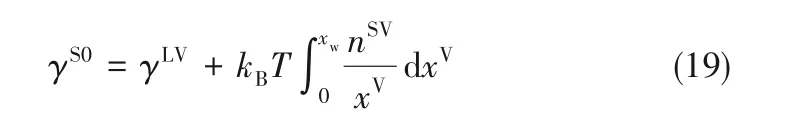
由团簇分布可知,石墨和二氧化硅的润湿压比分别为1.20和1.14。对于吸附质水蒸气,气液界面张力γLV为0.0724 J/m2,因此,由式(19)计算得到的石墨和二氧化硅表面张力分别为0.086 J/m2和0.342 J/m2,与文献[37]中所报道石墨的表面张力值吻合较好,误差为2.4%。将已得到的γS0值代入式(17),可绘制气固界面张力γSV随压比的变化曲线,如图8所示,随着界面吸附量的逐渐增加,界面能逐渐减小,气固界面张力不断降低,直至形成固液界面。
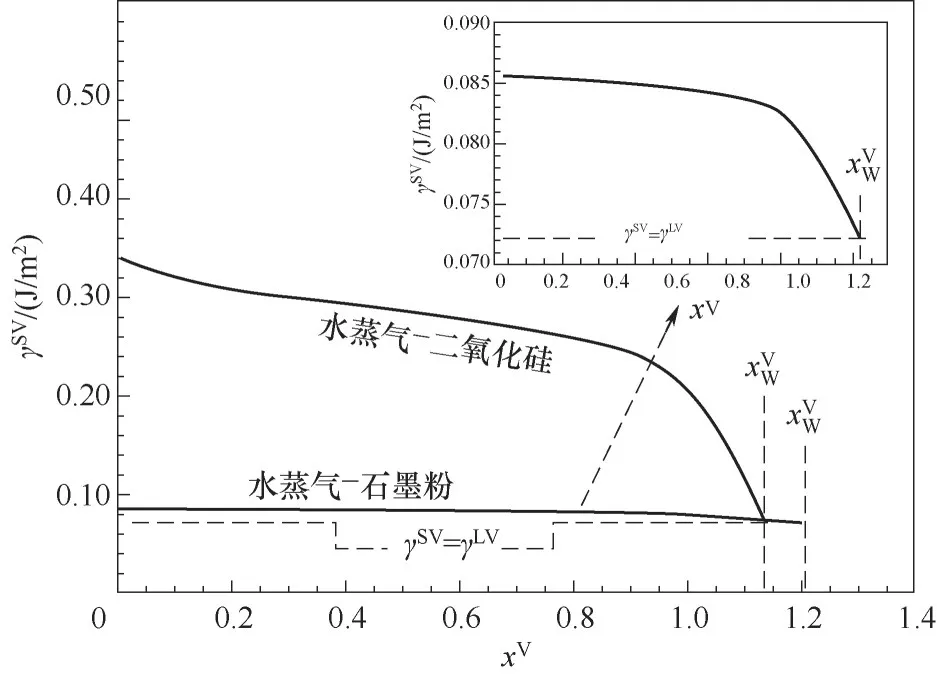
图8 气固界面张力随压比变化规律Fig.8 Variations of surface tension at solid-vapor interface with pressure ratio

图9 不同压比下界面张力变化率随压比变化情况Fig.9 Pressure ratio dependence of the variation of surface tension


3结 论
采用实验测量和理论分析相结合的方法,研究了水蒸气在石墨及二氧化硅表面的吸附特性,分析了气固界面的吸附行为及团簇演变规律,获取了零吸附条件下固体表面张力,确定了吸附相变及润湿发生条件,具体结论如下。
(1)Zeta吸附模型理论预测值不存在奇异点问题,且在整个吸附压力区间理论预测和实验测量结果吻合很好。明确了气体分子以团簇形式吸附在固体表面,吸附开始瞬间,零吸附单元数量迅速下降,单分子团簇数量增加。低压比区小分子团簇占据主导地位,随着压比的增加,含不同分子数的团簇逐渐增多,界面吸附量及气固界面张力变化率逐渐减缓。
(2)当压比趋于1/α时,吸附量陡增,吸附量变化率增加至最大值,此时界面各种类型团簇出现概率相等,团簇类型最多,吸附层内混乱度最大,吸附熵达到极值,界面吸附发生一阶相变。随着压比的进一步增加,小分子团簇逐渐减少,性质均一的大分子团簇占据主导地位,形成类液膜。
(3)确定了零吸附条件下二氧化硅和石墨的表面张力分别为0.086 J/m2和0.342 J/m2。随着吸附量的增加,气固界面能减小,界面张力随之减小。在润湿压比条件下,界面张力变化率达到极值。由于氢键的作用,使得二氧化硅-水界面吸附量及界面张力变化率远大于石墨。
符号说明
aζ——单位面积上含有ζ个分子的团簇数量,μmol/m2
c——Zeta等温常数
kB——Boltzmann常数
M——单位面积吸附单元数
nSV——吸附量,μmol/m2
P——压力,Pa
qζ——含有ζ个分子团簇的配分函数
T——温度,K
xV——压比
α——Zeta等温常数
γ——表面张力,mJ/m2
ζ——团簇含分子数量
μ——化学势
Ω——配分函数
上角标
LV——气液界面
S——固面
SV——气固界面
S0——零吸附下的固体界面
V——气相
下角标
m——团簇含有的最大分子数量
w——润湿条件

