上软下硬地层隧道破坏规律数值模拟

李伟伟， 宋 鹏， 李明奇

(南阳理工学院土木工程学院 河南 南阳 473000)

当前，国内外学者针对隧道围岩和施工稳定性，通过理论分析、数值分析、室内试验等手段开展了较多的研究。例如，Bobet[1]通过理论解析模型计算分析了含水条件下隧道围岩和衬砌结构受力和变形响应，吴波[2]等针对常见围岩级别组成的5组地层，通过有限元数值计算对上软下硬地层隧道围岩稳定性量化评价标准进行了详细的分析和系统的研究。郑颖人[3]等提出了岩石围岩分级思路，并以无衬砌围岩安全系数作为各级围岩自稳能力的定量判据由此反推出各级围岩的力学强度参数，改善了参数的合理性。赵文娟[4]等采用正交试验和极差分析相结合的方法得出了影响上软下硬地层的两个主要因素是跨度和埋深。邵标[5]等依托大连地铁二号线兴工街站为实际工程背景，利用有限元软件对组合变形控制措施的施工效果进行分析，发现随着支护措施的逐渐加强，地表最大沉降值逐渐减小，并且双层初期支护和增设大拱脚对于控制地表沉降效果最好。

当前，国内外学者针对隧道变形问题有着大量的研究。刘国栋[6]通过超大断面浅埋隧道的特点，针对实际的工程地质情况进行了地表下沉、隧道拱顶沉降、衬砌收敛等监测等项目的监测分析。指出超大断面浅埋隧道采用不同开挖方式的自稳时空效应及各自优缺点，并为支护体系的优化提供了理论据。滑笑笑[7]以实际的工程地质情况为研究背景，基于RFPA软件把强度折减方法引入到隧洞围岩的稳定性分析中，并指出安全系数失稳判据具有可行，不同断面形状洞室围岩的破坏模式不同。研究人员[8-10]根据土体极限平衡原理和隧道周围统一土体移动模型，修正了土体变形的计算公式，使计算结果更加接近工程实际。张称呈[11]等分析了围岩压力和温度变化对盾构隧道衬砌应力变化的影响，采用MATLAB绘制了衬砌应力变化图，推导了衬砌应力计算公式，对衬砌应力变化规律进行了理论分析。冯星[12]结合具体工程分析了支护的变形机理，认为针对大变形措施控制的二次衬砌的最佳时间为7天，且必须保证一定的安全步距。

本文采用数值模拟的方式利用FLAC3D进行设计与分析，通过对比不同开挖深度的云图信息来探究随着开挖深度的变化，隧道围岩的变形和破坏情况，通过对比相同开挖深度的隧道处于不同位置的云图信息来探究隧道处于不同的工程地质的情况下的应力、应变等的变化，经过以上的应力、应变、剪力等云图的对比情况总结出隧道处于不同开挖深度的应力变化规律、变形情况、剪力变化情况，从而对实际的工程隧道开挖加以分析，综合提出合理的结论和建议。

1 模拟地层情况

模拟地层采用浏阳河隧道工程中的进口端DIIK1562+793～DIIK1652+960段工程地质为地质背景，大部分为平缓构造剥蚀低丘区，自然坡度为3～10°，最大海拔高度为83.79 m，最低海拔高度为23 m左右(浏阳河底)，隧道施工地区的断裂构造不发育，没有较大的断裂构造，局部的岩石风化不均匀，地下水量极小，且渗透性较差。

2 建模过程及岩层参数

2.1 模型的数值模拟

实际地层情况比较复杂，根据隧道位于软硬地层的不同位置，简化后的模型如图1所示。

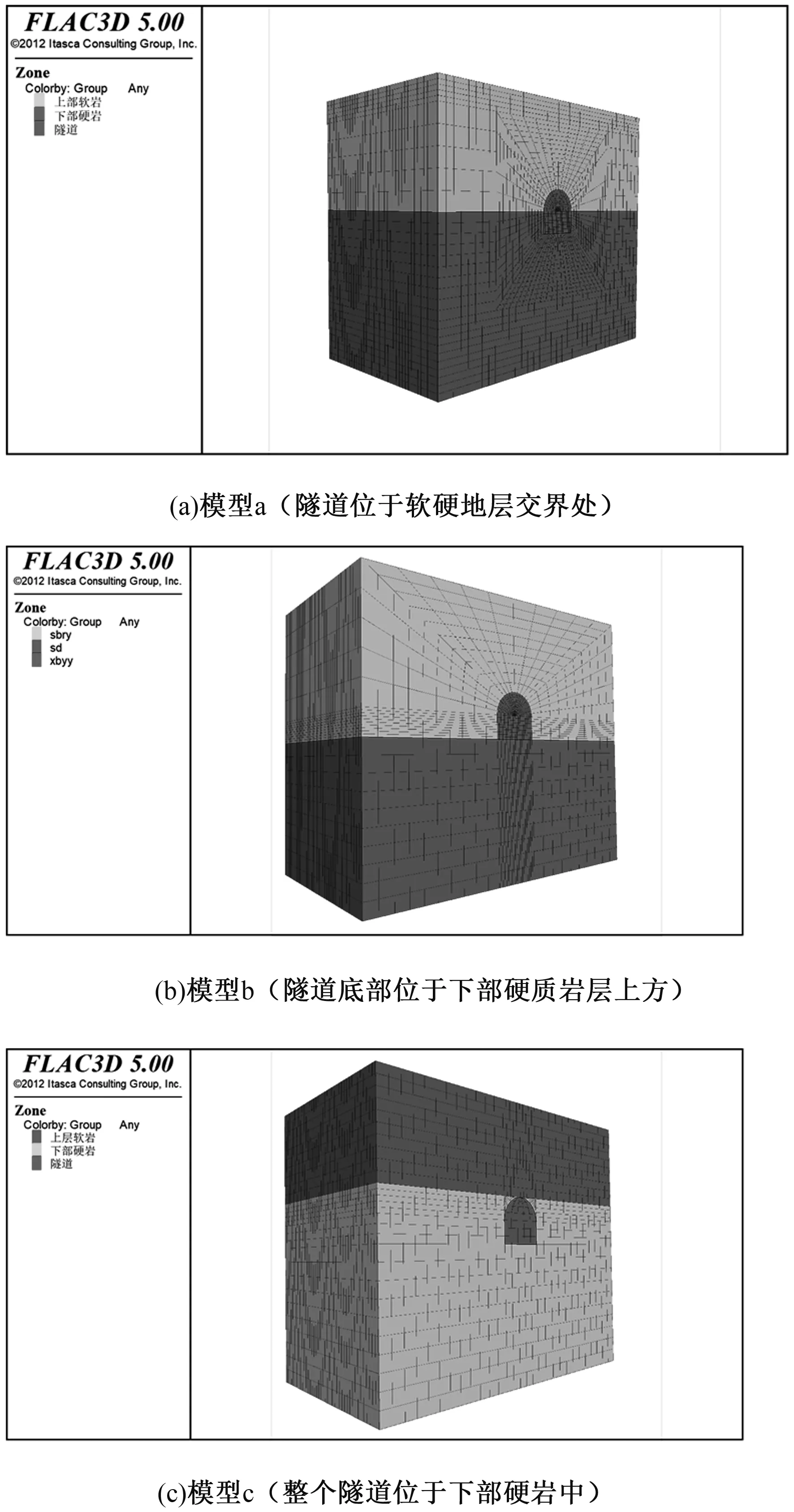
图1 模型数值模拟图

(1)隧道采用直墙半圆拱的形式，底部跨径为10 m，上部圆拱半径为5 m。

(2)简化后的隧道上部为软弱岩层，隧道底部为坚硬岩层，两地层之间的夹角为0°。

(3)整个模型具体参数为70 m×40 m×60 m，为了消除边界效应隧道建在模型正中心。

(4)隧道为浅埋隧道，隧道的埋深为20 m。

2.2 模拟地层隧道岩层参数

浏阳河隧道岩层各项参数如表1所示。

表1 围岩参数表

2.3 数值模型计算参数

FLAC3D中的模型在弹性范围内都由两个弹性常量来进行描述，即体积模量K和切变模量G在FLAC3D中，常用常量K和G，而不用弹性模量E和泊松比ν，它们之间的关系如下

K=E(1-2ν)
G=E/2(1+2ν)

不过上式在ν接近0.5时就不能用了，否则K值将接近无穷大，使解题收敛十分困难。

2.4 边界条件

边界分两类：真实边界和人为边界。真实边界存在于模型中的真实物理对象，如隧道面或地面；另一种是为了封闭单元体不得不假定人为设定的边界，施加于边界的力学条件有两大类：指定位移和指定应力。

FLAC3D中不能直接控制位移。为了对边界施加给定位移，需要指定速率v。实践中，为对系统的影响最小，v应小而步数N应大。可以使用APPLY、FIX和FREE命令来对已有模型的位移进行控制。APPLY命令对模型网格内外边界或对内部节点施加力学、流体和热边界条件，也可以对模型中的单元体施加力、流体源或热源。在使用时需注意关键字所指定的类型(如节点、单元体或面)，如果没指定范围，则施加到整个模型。FIX命令使所选节点的速率固定不变，或使孔隙压力和温度不发生变化。

2.5 隧道开挖

隧道开挖选择分步开挖的形式，每次开挖5 m，即每进行5 m的开挖进行一次求解计算，共分8步开挖完毕。

2.6 监测点的布置

隧道进行开挖的过程中为了更好地监测隧道位移变化规律，一般要设置监测点来进行位移的监测。

本隧道为隧道开挖围岩破坏规律的研究主要考虑的是监测隧道开挖过程中的位移变化量的变化情况。隧道开挖时，为了监测隧道的竖向位移变化情况和隧道水平位移变化情况，在隧道开挖时候分别在拱顶、两帮、直墙中部以及隧道底部中心点处共设置了8个监测点。

位移监测选择Z方向的位移变化情况和X方向的位移变化情况。在隧道开挖后可以观察到隧道开挖位移变形情况，各个监测点的布置情况如图2所示。

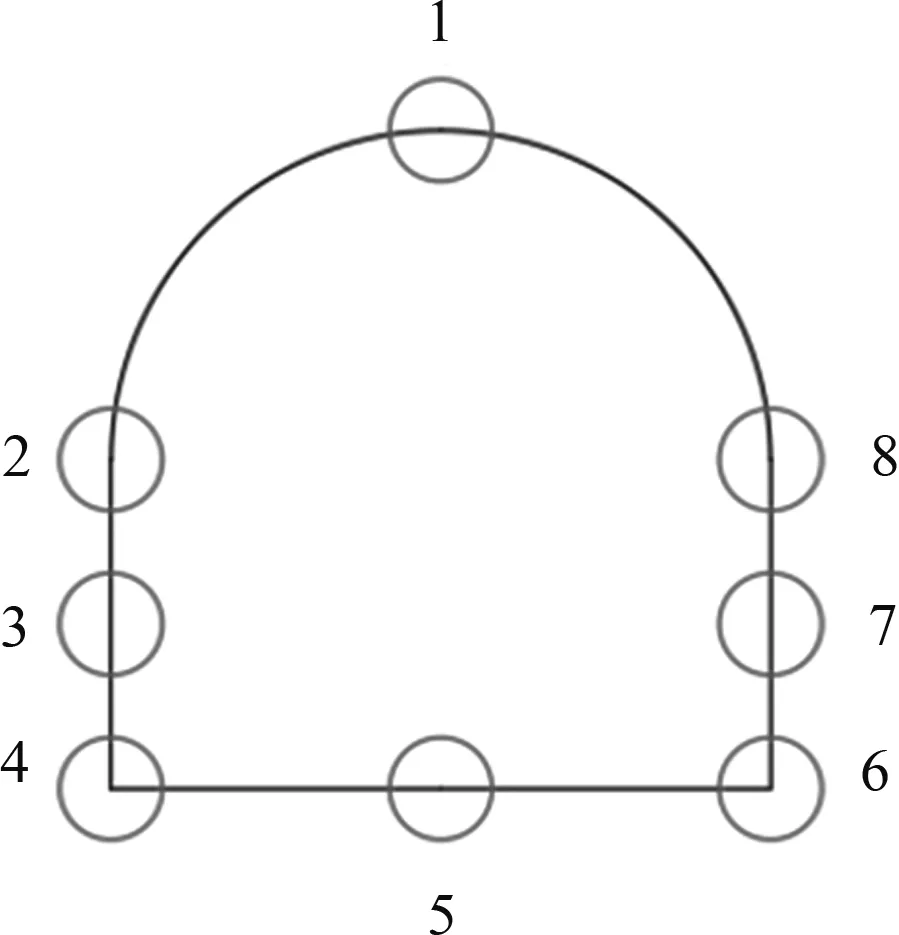
图2 监测点布置图

3 云图对比及监测点分析

3.1 垂直应力云图对比

从图3隧道开挖20 m时垂直应力云图中可以看出：模型a拱顶垂直压力为0.0048～0.1 MPa，拱底垂直压力为0.0048～0.1 MPa；模型b拱顶的垂直压力为0.0164～0.1 MPa，拱底的垂直压力为0.0164～0.2 MPa；模型c拱顶处垂直压力为0.0048～0.2 MPa，隧道底面的垂直压力为0.1～0.2 MPa。

图3 垂直应力分布图

隧道开挖40 m时，由图3分析可得模型a拱顶垂直压力为0.0054～0.1 MPa，拱底垂直压力为0.0054～1.39 MPa；模型b拱顶的垂直压力为0.0189～0.1 MPa；拱底垂直压力为0.1～0.2 MPa；模型c拱顶处垂直压力为0.0054 ～0.2 MPa，底面的垂直压力为0.2～0.4 MPa。

随着开挖深度的增加，3种模型隧道拱顶处的垂直应力随着开挖深度的增加而逐渐增加，隧道完全处于坚硬岩层时，隧道的应力变化范围最小，但应力范围最大(如图3)。

3.2 水平应力云图对比

随着隧道开挖，隧道的3种模型水平应力变化不大，处于不同位置的隧道水平应力大小的范围有所区别，当隧道完全处于下部硬岩的情况下，隧道的拱顶部分的水平应力和隧道两帮位置的水平应力要比前两种情况大(如图4)。

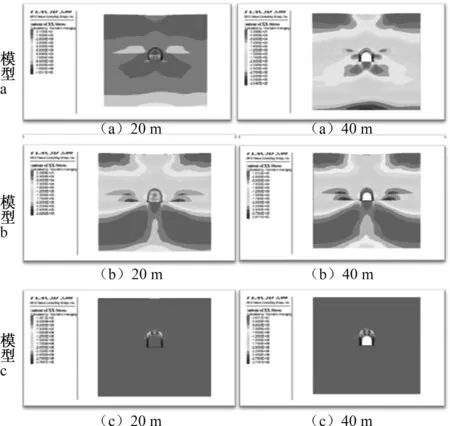
图4 水平应力分布图

3.3 剪应力云图对比

由图5可知，随着隧道开挖，3种模型的剪应力变化很微小。剪应力几乎不随隧道开挖而变化，但是剪应力的应力范围却有所区别，而且当隧道完全处于坚硬岩层的时候，隧道的剪应力值最大。

3.4 竖直位移云图对比

由图6可知，随着开挖深度增加，3种模型拱顶的竖向位移逐渐增加，隧道底部的竖向位移几乎不变，模型a隧道拱顶整体的竖向位移小于模型b。模型c完全处于下部坚硬岩层当中，隧道开挖时候竖向变形最小。

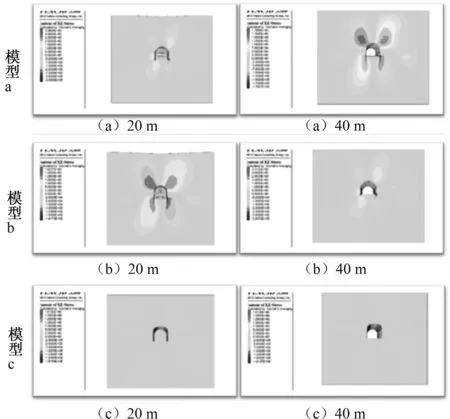
图5 剪应力分布图

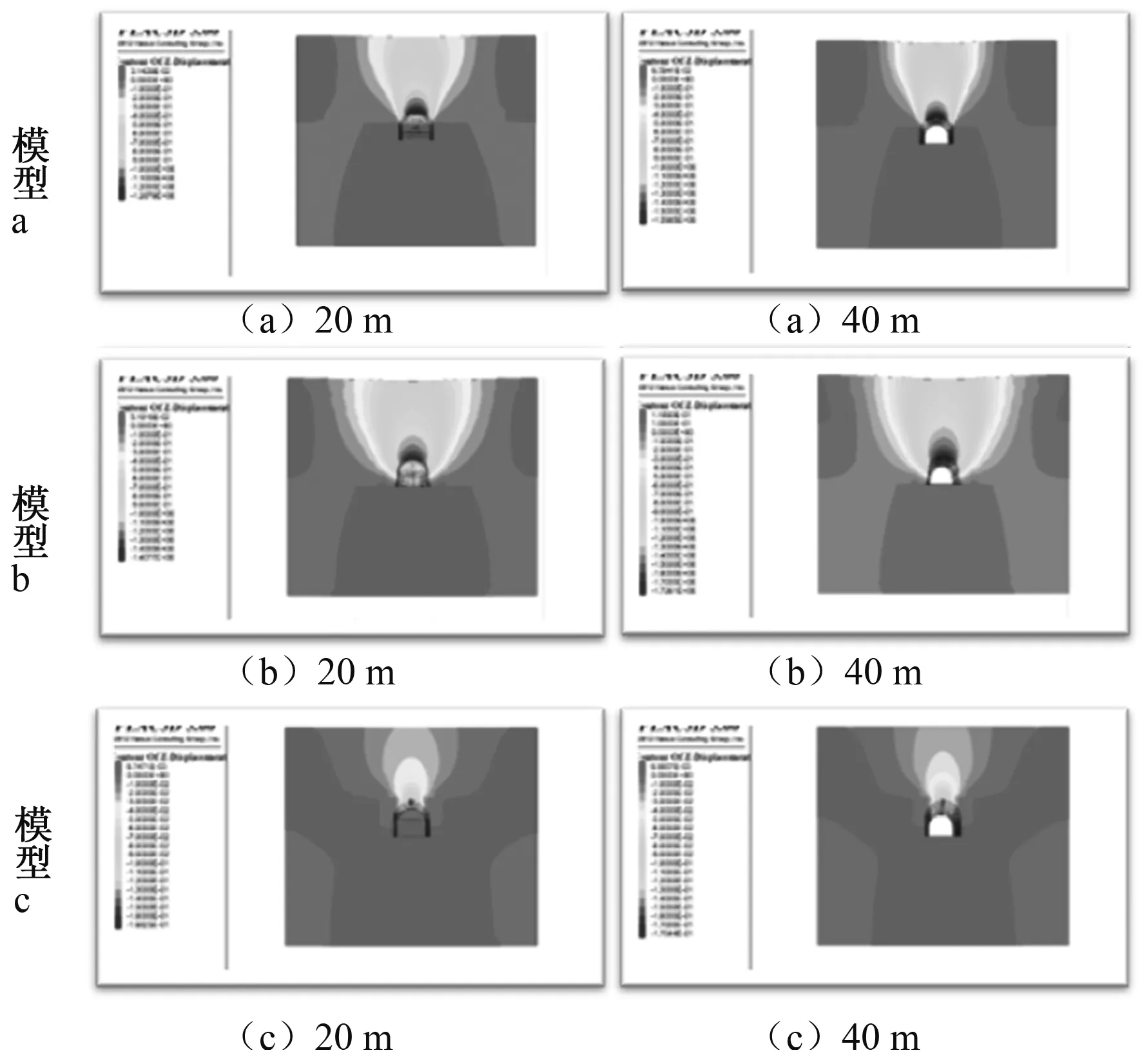
图6 竖直位移分布图

图7 水平位移分布图

3.5 水平位移云图对比

由图7可知，随着隧道的开挖，3种模型水平位移是不断变大的，处于不同地层中的隧道围岩变化的规律是不同的，模型a水平位移最大的位置处于隧道两帮处，模型b水平位移最大的位置是隧道的直墙部位，模型c水平位移最大的部位发生在拱顶处与水平面夹角为45°的方向。

3.6 监测点竖直位移变化情况

由图8可知，根据监测点变形情况分析，隧道拱顶下沉量最大，其余部分竖向变形量都很小。对于模型a，隧道开挖过程中，拱顶部分下沉量最大，其余部分竖向变形量几乎为0。对于模型b，隧道开挖过程中，拱顶下沉量最大，隧道的两帮位移次之，其次是隧道直墙中部，其余部分隧道的竖向变形量几乎为0。对于模型c，隧道开挖过程中，拱顶部分下沉量最大，隧道底部略微拱起，其余部分竖向位移几乎为0。

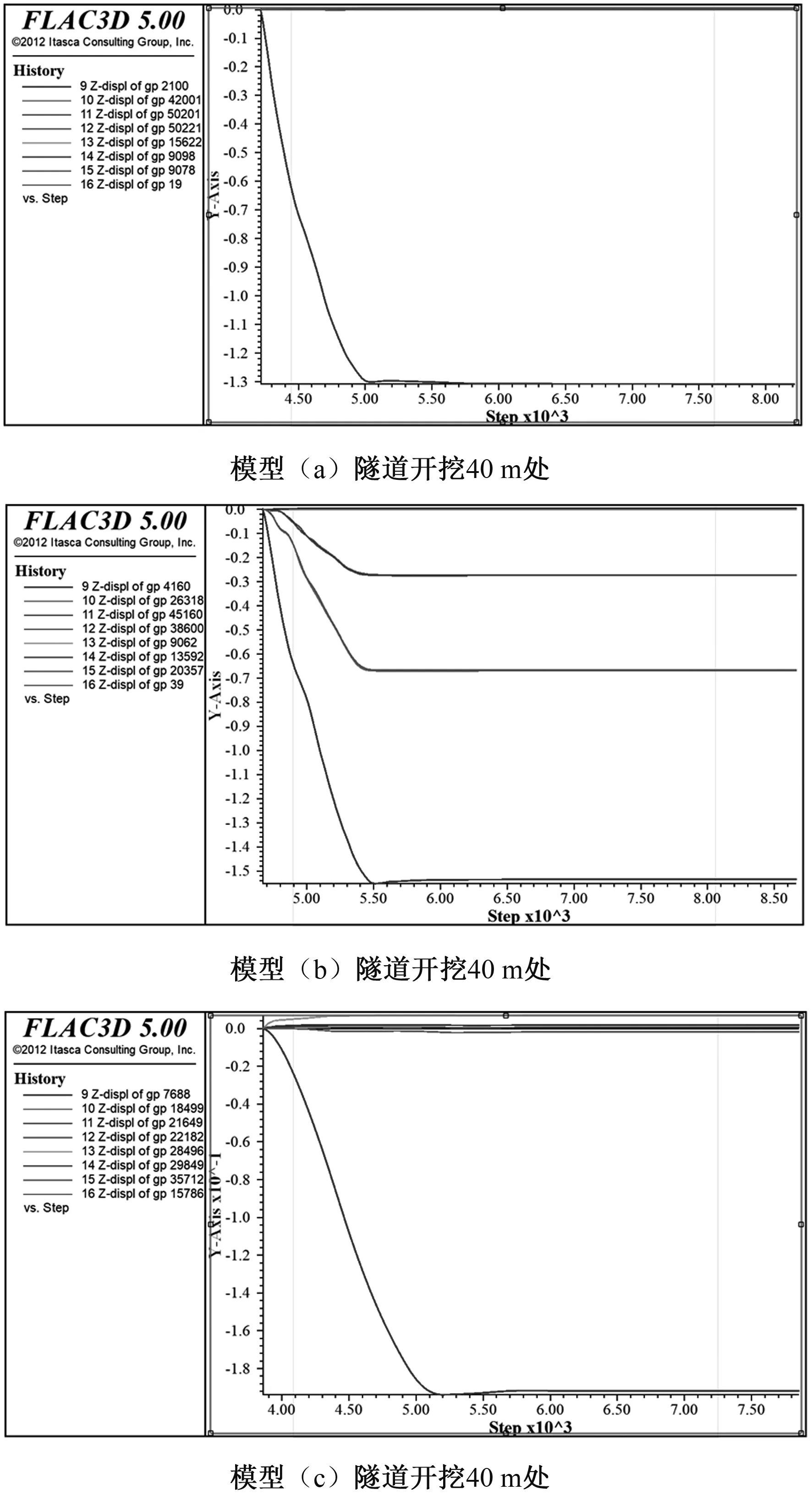
图8 竖直位移变化情况

3.7 监测点水平位移变化情况

由图9可知，根据监测点变形情况分析，隧道两帮水平变形量最大，其次是隧道的直墙中部分的水平变形量。3种模型水平变形量都是隧道两帮变形量最大，直墙部分次之，其余部分变形量几乎为0。

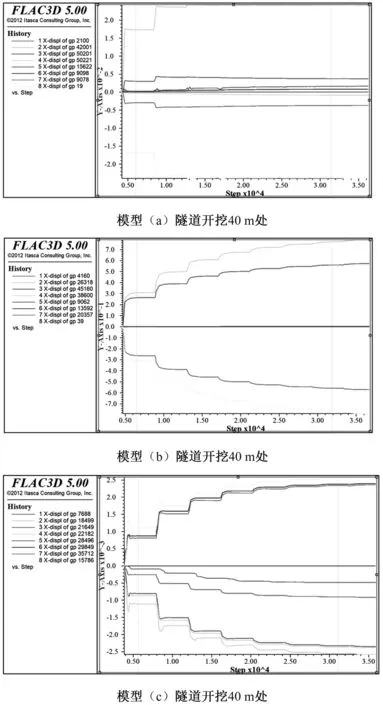
图9 水平位移变化情况

4 结 论

(1)随着隧道开挖，隧道的拱顶竖向位移逐渐增大，且隧道完全处于软弱岩层条件下时变形量最大，隧道处于坚硬岩层条件下变形量最小，3种模型隧道底部变形量均很小。

(2)随着隧道开挖，隧道的剪应力、两帮水平应力、垂直应力变化不大，但当隧道完全处于坚硬岩层条件下应力范围最大。

(3)随着隧道开挖，隧道两帮变形量逐渐加大，且隧道处于不同工程地质条件下隧道变形范围不同。隧道处于上软下硬地层中间时，变形最大位于隧道两帮位置，隧道处于软岩时，变形最大处于隧道中的直墙部分，隧道完全处于坚硬岩层时，隧道变形最大地方为隧道的拱顶部分与水平面倾角为45°的部分岩层。

(4)通过监测点的分析，隧道开挖过程当中，隧道水平变形量最大的部分为两帮竖直变形量最大的部分是隧道拱顶。